可压缩静压支撑抗偏载动态特性分析与优化

陆 亮， 陶 陶， 訚耀保， 朱康武

(1. 同济大学 机械与能源工程学院， 上海 201804； 2. 上海航天控制技术研究所， 上海 201109；3. 上海伺服系统工程技术研究中心， 上海 201109)

油缸是液压系统执行机构，服役过程通常要求处于理想的二力杆状态，仅承受轴向力，没有径向力.但面对火箭推进、飞行模拟器、大吨位起重机等工业应用，因径向惯性力作用、铰链径向摩擦力作用、轴向力方向与活塞杆轴线不重合以及活塞及活塞杆的重力方向与其轴线不重合等使用与安装因素，导致活塞杆上存在客观的径向力，加剧摩擦、增加泄漏、造成爬行，甚至导致工作失效[1].静压支撑因径向运动的反向压力反馈而产生抵抗偏载的作用，可使偏载活塞杆在新的位置重获稳定，实现油缸抗偏载应用的可能.就静压支撑理论与技术研究发展而言，国外研究起步较早，雷诺于19世纪80年代初步归纳了流体静压理论，经过百年发展逐步完善基础理论.后期研究主要围绕静压支撑性能优化展开，如美国的阿克伦大学的Dzodzo等[2]、德国Brecher等[3]基于数值模拟获得了静压支撑结构的局部流动细节，认为支撑面运动速度过快且油腔深度过小将导致油腔压力分布不均，甚至油腔出入口发生回流空化，严重影响支撑稳定性和可靠性.加拿大Ahmed与Marc[4]基于等效阻尼与等效刚度分析方法，进一步综合了油膜厚度、流动状态及静态承载之间的相互关系，但缺乏动态特性的深入剖析.法国Michaud等[5]则开始对静压油膜进行了热分析，认为静压承载与油膜温度取值和分布存在密切关系.静压支撑基础理论[6-9]在阻尼力、径向力、泄漏与润滑等物理机制与数学模型上已获得较为充分的研究，为其应用提供了广泛的帮助.

国内就静压支撑技术结合实际应用进行了大量的结构优化工作，取得了显著的效果.如20世纪90年代，华中理工大学肖金陵等[10]将锥形静压轴承应用于油缸，认为顺锥活塞杆可增加液压缸承载力，同时保证静压支撑的低摩擦和高精度.武汉科技大学牛晓阳[11]对支撑导向套性能进行了结构优化，设计静压支撑导向套及3个工字型油腔，发现在偏载作用下，此结构活塞杆拥有更好的对中能力.同济大学关景泰和徐宝富[12]则将静压支撑技术在桥梁与建筑激振试验中进行了成功的尝试，激振缸活塞杆两端采用了静压支撑密封，配合形成电液伺服振动实验台，能够很好地模拟振动实验.伴随配套技术的发展，航天装备关键部件制造甚至可以基于静压支撑技术实现了纳米级精度的竖直液体静压滑台[13]，而为了获得更高的控制精度，新型的基于超磁致伸缩薄膜控制的静压轴承节流器获得了较大的研究进展[14].

综上所述，在平稳或较小偏载驱动下，静压支撑动态过程对其工作品质影响不大，能在抗偏载的同时，获得低摩擦、高频响等优异性能，且伴随配套技术的发展，静压支撑技术的应用范围迅速拓展.

但目前静压支撑技术一般用于0～60℃温度工况，而火箭推力矢量系统通常服役于65～100℃高温工况[15].需要指出的是，油液介质中气体以溶解的形式存在不影响介质可压缩性，但伴随温度的升高，大量溶解气体析出，形成油气混合物，混合介质体积模量大大降低，由此将传统静压支撑技术应用于火箭矢量推力系统，介质可压缩承载成为需要着重考虑的问题.一般而言，对于10 MPa压力工况，当油液混有1%的气体时，其体积模量将降为纯油时35.6%，当混有4%的气体时，其体积模量仅为纯油时的12.2%，可见气体混合对体积模量影响之大.

由此可见，火箭等大型装备服役偏载冲击瞬间达千牛级同时长期处于65℃以上的高温环境时，介质可压缩性成为技术应用的关键问题，油缸径向分力阶跃冲击形成活塞杆振荡超调，过大偏心距导致油膜承载不可逆失效.本文就静压支撑局部高温可压缩介质流动对油缸抗偏载动态特性的影响进行分析，并提出优化改建的建议.

1 偏载状态静压支撑动态模型

油缸作为推力矢量控制系统中的执行机构，在系统中发挥着重要作用，其工作控制着火箭喷管的摆动.当油缸轴向加载时，径向惯性偏载会跟随轴向负载产生，其大小取决于摆动的角加速度及作动器自身重量.对于火箭推力矢量系统油缸来说，其偏载力矩为几百至几千N·m.在径向偏载的作用下，油缸活塞杆产生偏心运动，静压支撑油腔压力、流量、承载力发生动态变化.根据力平衡与质量守恒原则建立偏载下的静压支撑动态微分方程，并建立传递函数，进行静压支撑动态特性研究.

1.1 偏载状态静压支撑动态方程

(1)

式中：m为活塞杆质量；ξ为黏性阻尼系数；F(t)为随时间t变化的径向偏载力；e为活塞杆受力后产生的位移；Ae为静压支撑有效承载面积；pi1为高压油腔压力；pi2为低压油腔压力.

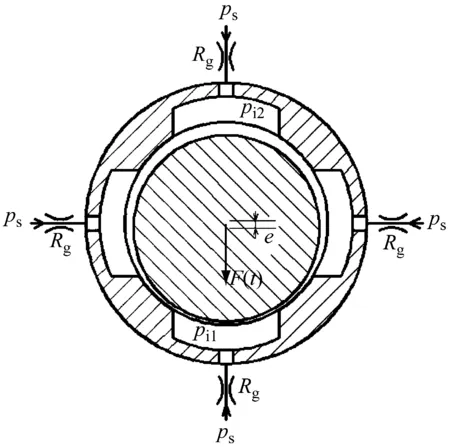
图1 活塞杆静压支撑状态简图

又根据流量守恒原理，进入一个工作油腔的流量与由一个工作油腔流出进入油膜间隙的流量相等，而该流量Q应为油腔在活塞杆未受力前排出的流量Qc、活塞杆受力后产生径向位移而挤压出的流量Qp以及由于高压下油液压缩性所产生的容积流量QV(V为可压缩油液体积)之和，如式(2).

Q=Qc+Qp+QV

(2)

活塞杆中心径向位移而挤压油液的挤压面积与油腔有效承载面积Ae相同，Ae可表示为

Ae=2R(L-a)·sinφ

(3)

式中：R为活塞杆半径；L为静压支撑轴向总长；a为静压支撑封油面轴向长度；φ为活塞杆偏位角.

高低压腔由于活塞杆位移导致油膜厚度变化而被挤出的流量分别可表示为

(4)

(5)

式中：h0为无偏心间隙；ε为活塞杆偏心率.

由油液压缩性造成的容积效应产生的流量QV可表示为

(6)

式中：τ为油液压缩系数；pi为油腔压力.

油腔在活塞杆未受力前排出的流量Qp可表示为

(7)

式中：Rh0为无偏心时静压支撑间隙液阻；A为偏心修正系数.

通过进油孔的总流量Q可表示为

(8)

式中：ps为供油压力；pi为油腔压力；Rg为外部节流器液阻.则高压腔流量连续性方程可表示为

(9)

低压腔流量连续性方程可表示为

(10)

将式(1)、(9)和(10)联立，获得偏载下静压支撑系统的数学模型.

1.2 偏载状态静压支撑传递函数

对于活塞杆受径向偏载力后产生位移到再次平衡，所建动态平衡方程与支撑系统流量连续性方程包含非线性项，求解过程较为困难，对于此类流体控制问题，通常采用局部线性化方法简化求解[16]，以此获得静压支撑不同结构与流动参数下静压支撑对偏载输入的响应，进而以此为依据优化结构参数.为此，将式(1)、(9)和(10)线性化，推导静压支撑系统传递函数G(s)，获得静压支撑动态特性研究的模型基础.

1.2.1微分方程线性化

基于泰勒级数展开，将方程非线性项使用隐函数表示，获得式(9)和(10)中局部项表达为

(11)

(12)

将f1与f2在初始工作点(ε0,pi0)附近展开为泰勒级数，表示为

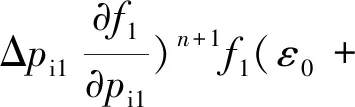
(13)

(14)

式中:Δε=ε-ε0；Δpi1=pi1-p0；Δpi2=pi2-p0；p0为无偏心时油腔压力，0<ζ<1.

忽略式(13)与式(14)中高阶小项，获得线性化方程，表示为

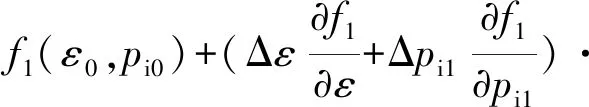
f1(ε0,pi0)

(15)

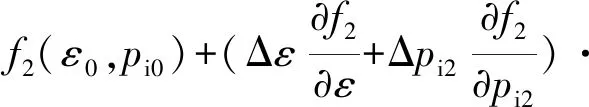
f2(ε0,pi0)

(16)

(17)

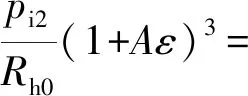
(18)

假设活塞杆初始位置为理想状态，即活塞杆无偏心，则此时偏心率ε0=0，Δε=ε，油腔压力pi0=p0，又Δpi1=pi1-p0，Δpi2=pi2-p0，式(17)、(18)简化为

(19)

(20)

由此获得偏载状态静压支撑动态方程线性化模型，如下所示:

(21)

1.2.2系统传递函数

将式(11)进行拉普拉斯变换获得支撑系统的传递函数，如式(22)所示.

(22)

(23)

2 静压支撑阶跃响应动态特性分析

图2给出了油缸火箭推力矢量控制系统执行机构示意图，在驱动火箭喷管运动过程中必然形成与油缸轴向不完全重合的力.研究所设计油缸公称压力14 MPa，活塞直径63 mm，活塞杆直径45 mm，正常工作时轴向力90KN.通常当径向力为轴向力的2%～5%时，径向力对油缸性能的影响已无法忽略，基于先前研究[17]中的阐述，火箭推力矢量系统油缸所承受的径向偏载力在几百至几千牛之间，且为瞬间加载，故研究取径向偏载力以阶跃信号特点作为系统输入，区间保持在1 800 N至4 500 N之间.对于液压工程技术而言，当需要考虑介质可压缩性时，通常取有效体积模量680 MPa，即式(6)中，1/τ=680 MPa，为通常体积模量取值的30%～40%[18].

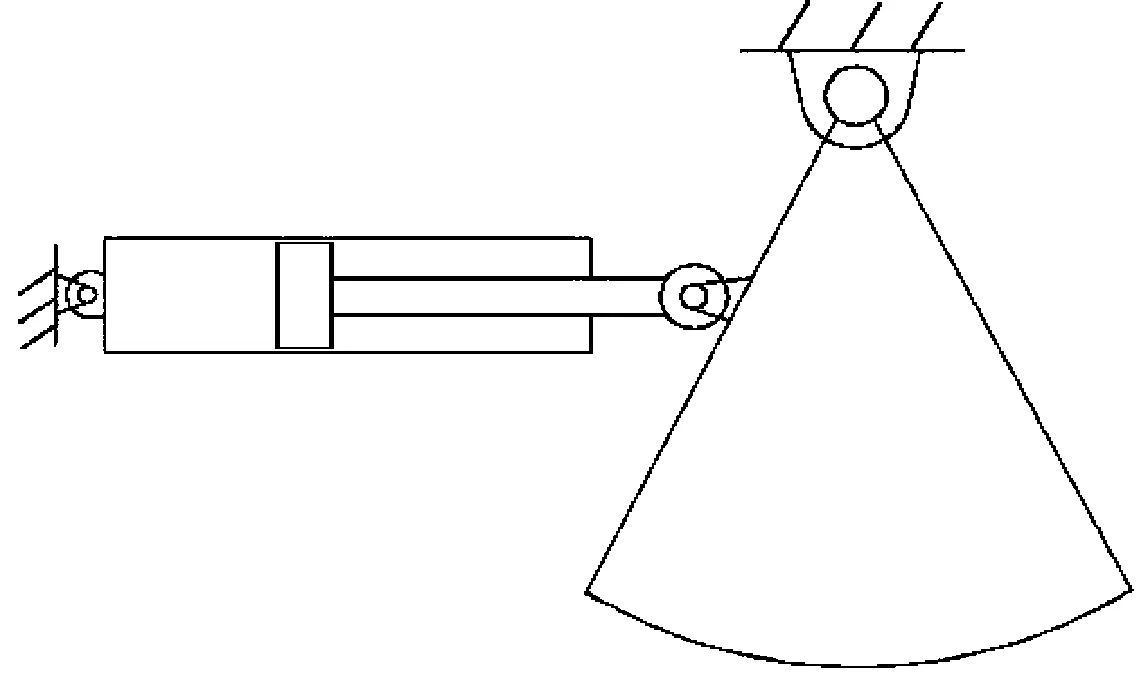
图2 火箭推力矢量控制系统执行机构示意[14]

图3首先给出了2 000 N中等阶跃力下，油膜间隙50 μm、静压支撑供油压力8 MPa～2 MPa时静压支撑动态特性的一般情况.由图可知，在结构参数不变情况下，活塞杆最终平衡位置伴随油腔压力的降低而愈发偏离轴心，或者说静压支撑抗偏载能力逐步退化，就超调响应而言，供油压力越高，越易发生.但供油压力(油腔压力)越大，抗偏载能力越强，如何在较高的供油压力下获得如图3所示的4 MPa响应曲线是研究目标，由此就结构优化进行进一步研究.

图3 阶跃载荷下不同油腔压力时活塞杆偏心率响应曲线

2.1 油腔深度最优区间

为获得更高的抗偏载能力，且同时保证响应曲线不过度超调而导致油膜破裂，取计算范围内较高阶跃力4 000 N，且供油压力提升至10 MPa.在可行的参数范围内，保持油腔面积不变，改变油腔深度(0.25 mm～2.00 mm).如图4所示，在保持油腔作用面积不变的情况下，油腔深度不会改变活塞杆最终平衡时的偏心率.考虑动态过程，发现深度大于1.00 mm均出现超调，而2.00 mm深度超调量已经超过1，此时油膜已经破裂不可逆，油缸无法按正常方式在新位置平衡，此种情况是要极力避免的.

图4 阶跃载荷下不同油腔深度时活塞杆偏心率

活塞杆动态过程出现位移超调，正是源于油液在高温高含气量条件下的可压缩性，而本文在动态方程建立中考虑了可缩性项，由此获得了不同深度条件下动态特性的基本认知.其内在机理在于当活塞杆受偏载力后，油腔与敏感油路油液受到压缩，由压缩性形成的力反弹存在滞后，形成位移超调.为获得超调状况的一般规律，基于式(23)传递函数，利用Matlab工具计算求解，获得超调状态分布的一般规律，如图5所示，取无偏心间隙与油腔深度比值h0/h作为度量，可见当h0/h大于0.05时，活塞杆动态响应无超调，由此获得油腔深度上限.

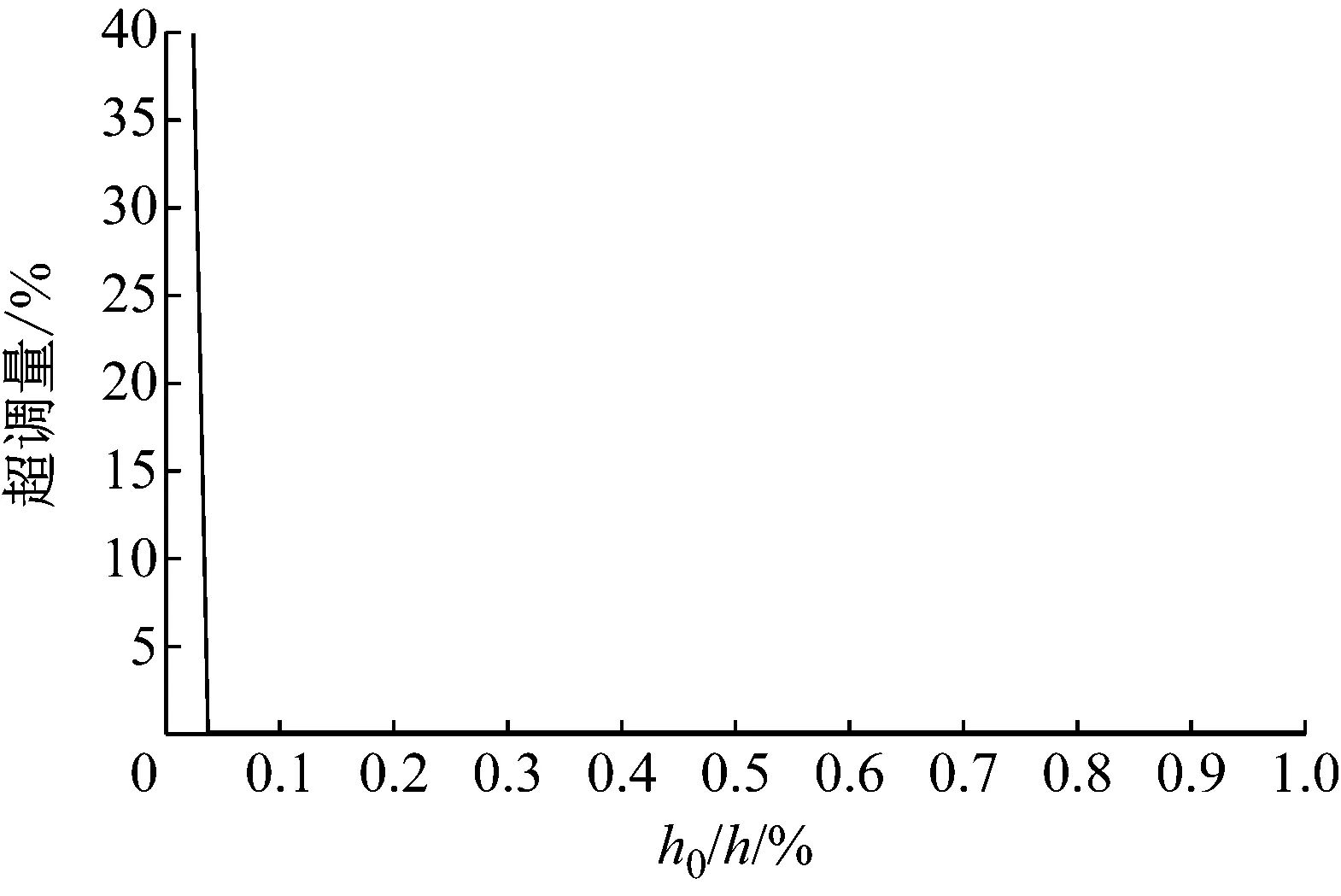
图5 油腔深度与超调量关系

由此可见，更浅的深度能够减少超调，并获得相同的抗偏载能力.但实际上过小的油腔深度导致油腔的节流作用就变得不可忽略，油腔出入口压力将不能假定为一致，而需建立严格的方程估算稳态承载能力.如图6所示，当油腔深度变小到接近油膜间隙时，油腔的节流作用就会变得不可忽略，静压支撑的稳态承载力也会受到影响.

图6 静压支撑轴向简图

图中p1、p3为油腔入口压力，p2、p4为油腔出口压力.油腔液阻Rc可由平行板节流公式近似得到，其表达式为

(24)

式中：μ为油液黏度；r为油腔中心到封油面的距离；b为油腔宽度.则油腔出口压力p2、p4可表示为

p2=p1-RcQ1

(25)

p4=p3-RcQ2

(26)

式中：Q1、Q2为油腔流量.静压支撑承载力Fb可表示为

Fb=(p1-p3)A1+(p2-p4)(A1+A2)

(27)

式中：A1为油腔面积；A2为封油面面积.

基于式(24)至(27)，图7给出了h0/h与静压支撑承载力之间的关系.由图可见，当h0/h大于0.1时，油腔深度与油膜间隙接近，油腔节流作用更为显著，油腔压力分布不均，油腔出口压力小于入口压力，同时高压腔压力降幅高于低压腔，压差减小，静压承载力减弱.故仅h0/h小于0.1时，油腔深度足够大，足以忽略节流作用而保证原有承载力.

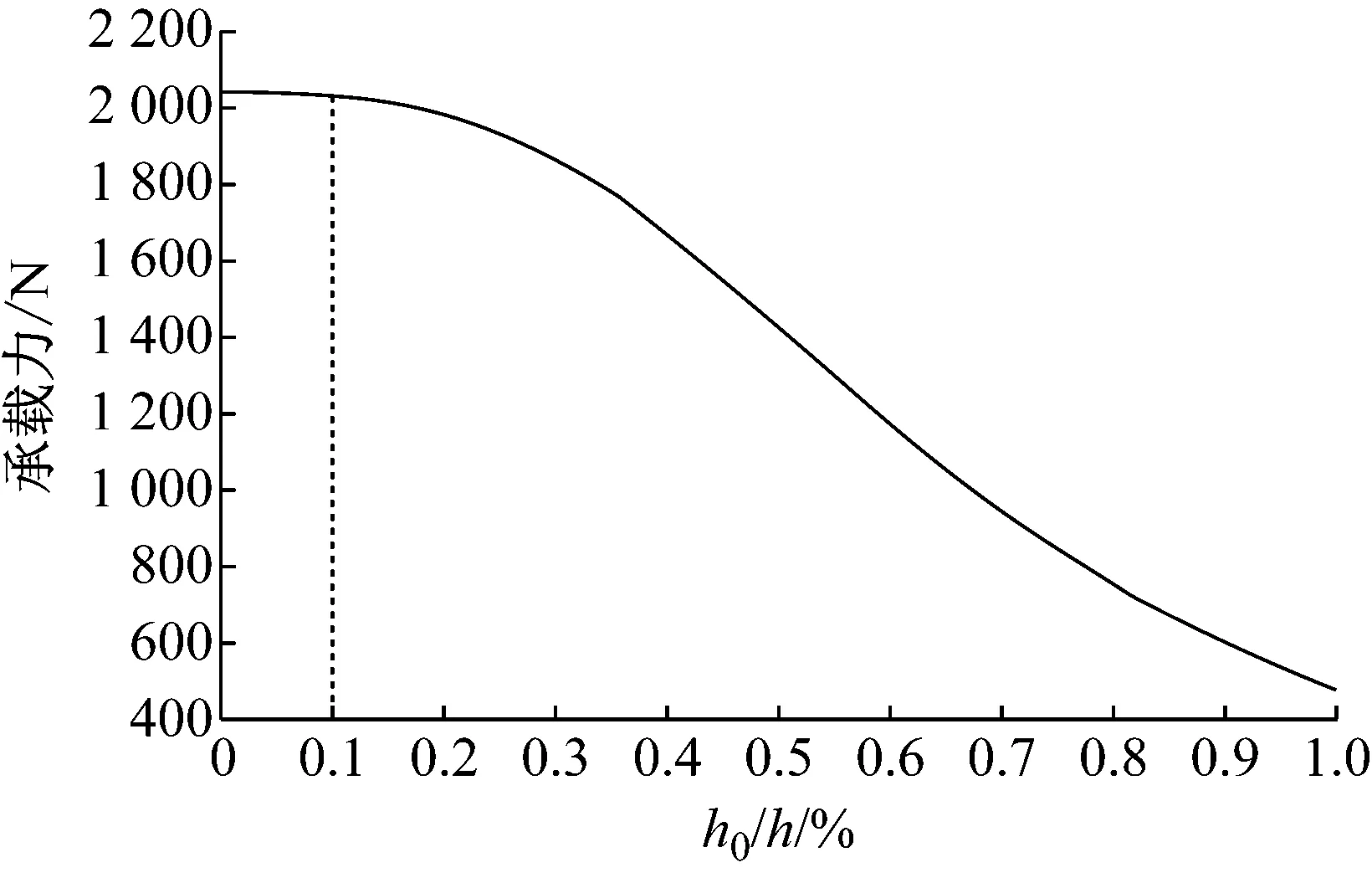
图7 油腔深度与承载力关系

综上，基于活塞杆无超调限制，h0/h需大于0.05，同时基于能够同步维持原有承载力，h0/h需小于0.10，由此获得油腔深度h优化适用区间为10h0～20h0.

2.2 油腔型面结构优化

如上所述，在不改变油腔面积前提下，更小的油腔深度能够减弱超调发生的风险，而动态超调直接取决于介质体积的可压缩性.由此不再改变油腔深度，通过合理的油腔型面变化来减小油液体积，则可进一步提升动态响应的平稳性，减少超调的发生，甚至减少泄漏流量.由上可知，油腔最小深度必须大于10h0，则此处论证型面优化时，取油腔入口深度10h0(h)，并在其后开设锥形腔体，减少承载油液的体积，其结构简图如图8所示，其中h1为油腔出口深度.

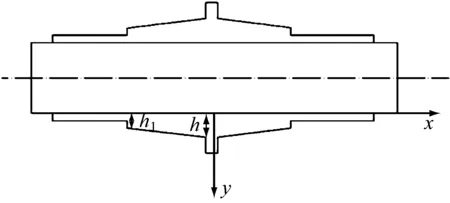
图8 锥形油腔静压支撑轴向简图

通过计算获得图9所示油腔出口深度与油腔深度比值h1/h与静压支撑承载力之间的关系，当h1/h≤0.25时，静压支撑承载力显著不足；但h1>0.25后，将能够维持足够的承载力，并有适当增加的趋势.

图9 h1/h与承载力关系

如若h1取0.25h时，在保证承载力前提下，可进一步减少35%的油腔体积，进一步降低超调风险，甚至减少泄漏流量.

3 结论

火箭推力矢量控制系统采用静压支撑取代传统密封，以获其抗偏载、低摩擦、高频响的优异性能，但服役工况极限温度高、温度跨度大，支撑结构局部介质流动处于高温高含气量恶劣状态，介质强可压缩性诱发活塞杆偏载振荡超调，限制了静压支撑技术在火箭推力系统应用中的推广.

对火箭推力系统油缸偏载静压支撑进行动力学建模与局部线性化分析求解，理论上获得了静压支撑结构深度的最佳适用区间，保证维持足够支撑力的同时降低超调发生的风险，避免超调过大导致油膜不可逆破裂失效事件的发生.在此基础上，进一步基于锥形腔体的型面优化设计，降低超调风险并维持支撑力，同时最大可减少35%的油腔体积，且同步减少泄漏损失.