基于构件合力的曲线梁桥最不利激励方向确定
冯睿为, 劳天鹏, 邓通发, 袁万城
(1. 同济大学 土木工程防灾国家重点实验室, 上海 200092; 2. 广州大学 广州大学-淡江大学工程结构灾害与控制联合研究中心, 广东 广州 510006; 3. 江西理工大学 建筑与测绘工程学院, 江西 赣州 341000)
曲线梁桥具有能够克服地形、地物的限制、结构线形优美、流畅等优点,广泛应用于城市高架及高等级公路工程中.受上部结构曲率的影响,荷载作用下曲线梁桥会产生弯扭耦合效应,特别是在地震动作用下,该效应尤为显著,使得曲线梁桥中构件的力与位移需求被放大,结构受到更为严重的破坏[1].在近年来发生的大规模地震中,曲线梁桥受损的案例屡见不鲜[2-4],更值得注意的是,由于地震动的激励方向具有较强的随机性,不同激励方向下结构的地震响应有所差异,特别是对于曲线梁桥这种几何形式及受力状态相对复杂的结构而言,地震动激励方向对结构地震响应的影响更加不容忽视.已有研究表明:对于不同激励方向,曲线梁桥的地震响应最大相差80%[5].因此,为保证结构抗震设计的可靠性,需确定结构产生最大需求时所对应的地震动激励方向,即结构的地震动最不利激励方向[6]. 目前在实际工程中最为常用的方法是将地震动每隔一定角度进行输入,通过比较各激励方向下的结构响应来确定最不利激励方向(简称全角度输入法),虽然该方法可以得到较为可靠的结果,但是计算量大且相对费时,对于大型工程及复杂结构而言适用性较差.鉴于上述原因,国内外研究人员提出了一些直接确定结构地震动最不利激励方向的理论方法,如反应谱法[6-8]、随机振动理论法[9]、时程分析法[10]、能量方法[11]等.对于曲线梁桥而言,全伟等[12]基于时程分析提出了确定结构最不利激励方向的简化算法,该方法通过2次时程分析便可求得地震动最不利输入角度;宋波等[13]基于推倒分析方法利用桥墩曲率来确定地震动最不利激励方向,孟杰等[14]利用Bresler屈服面并结合时程分析提出了确定地震动最不利激励方向的方法.
然而,尽管目前国内外关于确定结构最不利激励方向方面的研究取得了较大进展,一些新颖的计算方法相继被提出,但在结构最不利激励方向的判别标准方面仍值得进一步探讨,特别是部分方法以控制结构抗震设计的主要构件主轴方向的响应分量为判别标准的情况,这较难综合反映构件截面整体的受力性能,而且不同响应分量所对应的最不利激励方向往往不同,构件整体的最不利输入方向较难统一.尤其对于曲线梁桥,由于结构几何线形的不规则性,各个构件的主轴方向往往不同,因此结构主要构件的最不利激励方向更加难以预测.此外,部分方法在执行过程中仍需要较大的计算量,对于曲线梁桥等结构布置及受力行为相对复杂的结构而言实用性不高.
基于反应谱理论,以主要构件的合力或合位移为判别标准,研究一种确定结构地震动最不利激励方向的方法(简称构件合力法),并应用该方法确定一座典型曲线梁桥的地震动最不利激励方向,再与全角度输入法所得结果进行比较分析.
1 构件合力法的理论推导
基于实际工程抗震验算中常采用的单向地震动激励[15-16]提出构件合力法.如图1所示,X、Y轴为整体坐标轴,2、3轴为构件局部坐标轴,假定地震动为宽带平稳随机过程,地震动a(t)与X轴成θ角,θ沿逆时针方向旋转为正,构件合响应R(位移、内力、应力等)方向与2轴成α角.

图1 单向地震动激励下构件坐标轴方向规定
Fig.1Regulationforcoordinateaxesofacomponentsubjectedtoaunidirectionalseismicexcitation
由多质点体系的振动方程可知,质点的t时刻位移矢量δ(t)可以分解为
(1)
式中:φ=[φ1φ2…φi…φn],为振型矩阵;η(t)=[η1(t)η2(t) …ηi(t) …ηn(t)]T,为广义坐标矩阵;i、n为模态号.从而构件2轴方向的响应R2(t)可以通过质点位移向量的线性组合表示.
(2)
式中:q2为R2(t)所对应的响应传递矩阵,它是结构几何属性和弹性属性的函数.将式(1)代入式(2)中,可得
(3)
式中:ai为第i阶模态的有效模态内力向量[17].
(4)
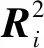
(5)
式中:ηi,max为第i阶模态的广义坐标峰值.
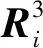
(6)
(7)
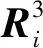
综合式(3)和式(6),构件的合力R(t)可以通过式(8)得到
R(t)=R2(t)cosα+R3(t)sinα=
(8)
基于以上理论公式的推导,当地震动沿任意方向θ输入时,构件的峰值合响应可以通过以下3个步骤得到.

(9)
(10)
式中:ηiX,max为Sa沿X向作用时第i阶模态的广义坐标峰值.
根据式(8),构件的合响应RX(t)可以表示为
(11)
式中:ηiX(t)为Sa沿X轴作用时第i阶模态的广义坐标.从而构件第i阶模态的合响应峰值RiX可以通过下式计算得到:
RiX=(aicosα+bisinα)ηiX,max
(12)
(2) 步骤2.将Sa沿Y轴方向作用,与等式(11)、(12)推导过程相同,构件合响应RY(t)及第i阶模态的合响应峰值RiY可以表达为
(13)
RiY=(aicosα+bisinα)ηiY,max
(14)
式中:ηiY(t)为Sa沿Y轴作用时第i阶模态的广义坐标;ηiY,max为Sa沿Y向作用时第i阶模态的广义坐标峰值.
(3) 步骤3.将Sa沿任意方向θ作用时,构件第i阶模态的合响应Riθ(t)可以通过式(15)得到:
(15)
式中:RiX(t)、RiY(t)分别为Sa沿X、Y向作用时构件第i阶模态的合响应.由多质点体系的振动方程可知
ηiX(t)=γiXηi(t)
(16)
ηiY(t)=γiYηi(t)
(17)
式中:γiX、γiY分别是X、Y方向第i阶振型的振型参与系数,从式(16)及式(17)中可以看出ηiX(t)与ηiY(t)完全相关,它们的比值为γiX/γiY,其峰值同时出现,因此构件第i阶模态的合响应峰值Riθ为
(18)
利用CQC(complete quadratic combination)模态组合方法[18]对Riθ进行组合可得到地震动沿任意角度θ激励时构件的合响应峰值表达式如下:
(19)
式中:ρij为模态组合系数;D1、D2、D3是合响应方向α的函数,可通过式(20)~(22)计算得到:
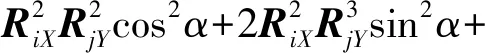
(22)
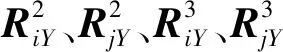
根据式(19)~(22)编制计算程序进行极值分析,可分别确定地震动最不利激励方向及最大响应方向,具体方法如下.
(1) 地震动最不利激励方向.首先给定θ范围,在每一个给定的θi下,依次循环α,求出地震动激励方向为θi时构件的合响应峰值Rθi,max,再分别比较各个激励方向下的Rθi,max,从而确定构件合响应最大值Rθ,max所对应的激励角度,即为最不利激励方向.
(2) 最大合响应方向.首先给定α的范围,在每一个给定的αi下,依次循环θ,求出各地震动激励方向下构件α方向的合响应峰值Rαi,max,再分别比较构件不同合响应方向下的Rαi,max,从而确定构件合响应最大值Rα,max所对应的响应方向,即为最大合响应方向.

2 数值模型建立及地震动选择
2.1 工程概况及有限元模型
选取一座典型的三跨钢筋混凝土曲线梁桥为工程背景,该桥整体布置及主要构件截面尺寸如图2所示.该桥曲线半径为90 m,每跨跨径均为30 m;上部结构为单箱单室箱梁,采用C50混凝土,梁宽8.5 m,高1.9 m;相邻联间设置伸缩缝,伸缩缝宽0.1 m.下部结构采用双柱墩,材料为C40混凝土,墩高均为6.0 m,直径为1.0 m,全桥采用板式橡胶支座,主梁与桥墩间除支座外无其他墩梁连接装置.
采用有限元分析软件SAP2000建立曲线梁桥有限元模型,考虑相邻联间耦联振动的影响,该有限元模型包括左右两侧边界联,边界联均为跨径30 m的简支梁桥,截面尺寸及构造与主桥相同.全桥主梁和桥墩采用弹性梁单元模拟;支座采用线性连接单元模拟,主桥中墩支座(B3至B6)水平刚度均为3 571 kN·m-1,主桥边墩支座(B1、B2、B7、B8)及引桥支座水平刚度均为2 142 kN·m-1,有限元模型中不考虑防落梁装置对结构地震响应的影响.不考虑桩-土相互作用对结构的影响,墩底采用固结的方式处理.
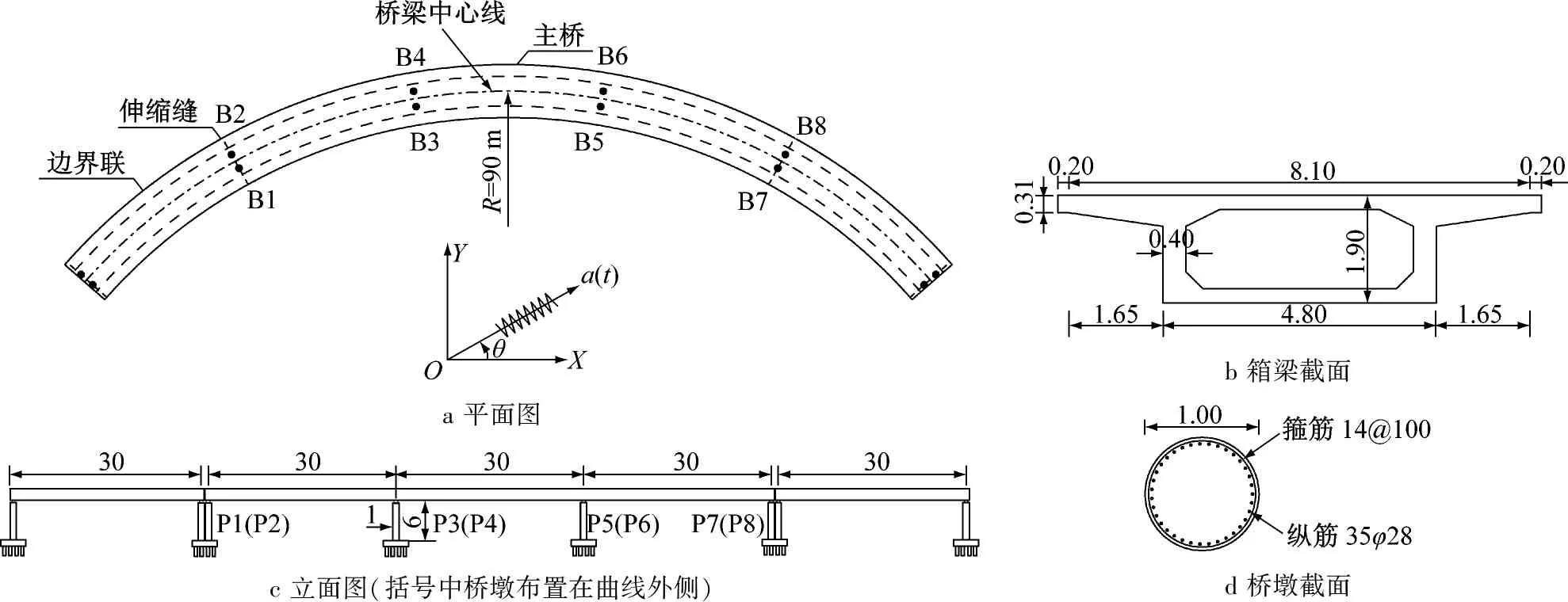
a 平面图c 立面图(括号中桥墩布置在曲线外侧)b 箱梁截面d 桥墩截面
图2曲线梁桥整体布置及截面尺寸(单位:m)
Fig.2Configurationandgross-sectionaldimensionofthecurvedbridge(unit:m)
对该桥进行动力特性分析,考虑结构前12阶模态对结构响应的贡献,各阶模态周期如表1所示.
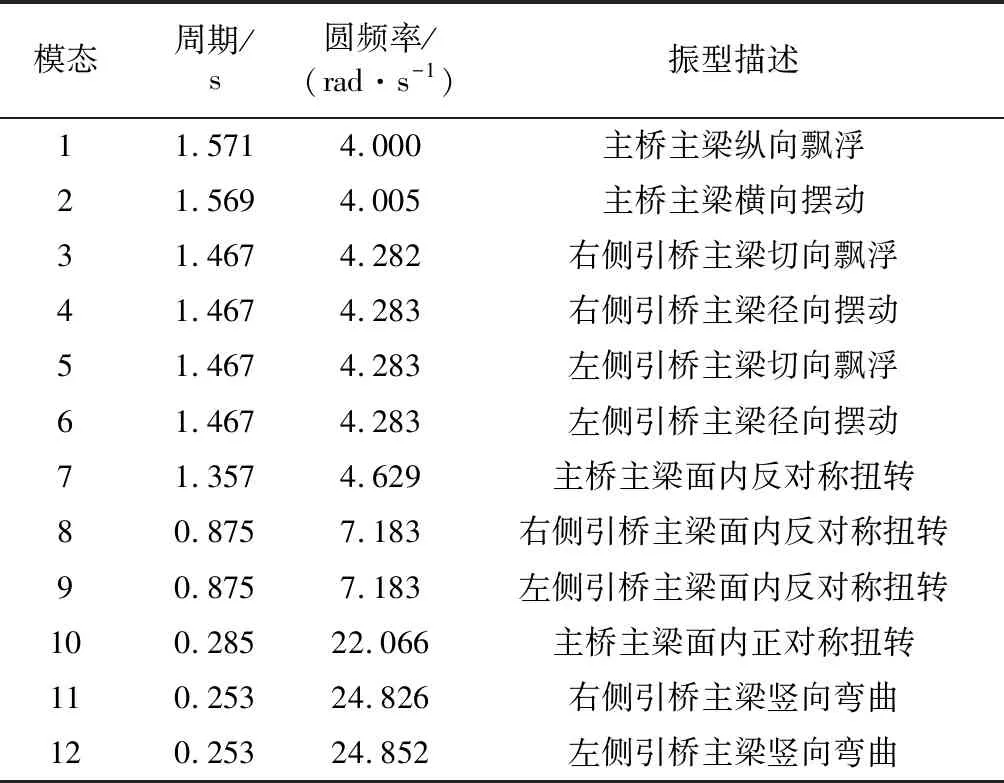
表1 曲线梁桥振动周期
2.2 地震动选择及坐标轴方向规定
选取3条具有不同特性的地震波.其中1994年的Northridge(Rinaldi)是地面运动速度较大的近场脉冲型地震动,1994年的Northridge(Santa Monica City Hall)地震动具有峰值加速度较大、地震动频率较高等特点,而1989年的Loma Prieta(Saratoga Aloha Ave)代表中等强度的地震动.3条地震动的反应谱如图3所示,由于该桥几何布置关于Y轴对称,因此θ范围可取为0°≤θ≤180°[19].另外,由于主桥外侧中墩分担上部结构惯性质量较大且边墩支座水平刚度较小,位移响应会比中墩支座大,因此选择P4墩墩底弯矩及B2支座位移来反映结构的整体响应,P4墩及B2支座的整体及局部坐标轴方向如图4所示.其中β1、β2代表2轴与整体坐标系X轴间的夹角.
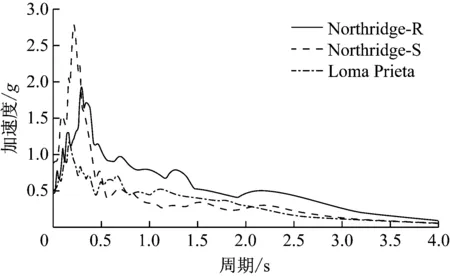
图3 所选地震动反应谱

a P4墩坐标轴方向b B2支座坐标轴方向
图4构件坐标轴方向规定
Fig.4Regulationforprincipleaxesofcomponents
3 构件合力法的应用及结果分析
应用构件合力法确定曲线梁桥的最不利输入方向,以Northridge(Rinaldi)地震作为输入,阐述该方法的应用过程.首先,基于表1中动力特性分析结果,依据文献[18]计算模态组合系数ρij;然后分别在X、Y方向输入地震动,对算例桥梁进行反应谱分析,得到桥墩及支座局部坐标轴(2、3轴)方向各阶模态的峰值响应,如表2所示;最后将计算得到的模态组合系数ρij及表2中模态响应分量的峰值代入到式(20)~(22)中,通过编制计算程序建立构件合力峰值与激励角度及截面合力方向之间的关系,分别如图5、图6所示.从图5中可以看出在Northridge(Rinaldi)地震作用下,θ=45°为该桥最不利激励方向,当地震动沿该方向作用时桥墩弯矩及支座位移均达到最大.此外,各构件响应对于地震动激励方向的敏感性有所不同.对于墩底弯矩而言,如图5a所示,θ=45°时墩底合弯矩为5 990.7 kN·m,而当激励方向θ=135°时,墩底弯矩为5 674.6 kN·m,不同激励方向下墩底弯矩最大值与最小值相差5.3%,说明地震激励方向对于桥墩受力影响较小.这主要归因于桥墩采用圆形截面,各方向力学性质相同,因此不同激励方向地震动作用下墩底响应之间差异较小,若桥墩采用非圆形截面,此时截面力学性质存在各向异性,则地震动激励方向对于桥墩受力的影响有可能增大.相比之下,通过图5b计算可得,不同激励方向下支座位移峰值最大相差15.2%,说明地震激励方向对支座位移的影响不容忽视.

表2 桥墩及支座局部坐标轴方向各阶模态峰值响应
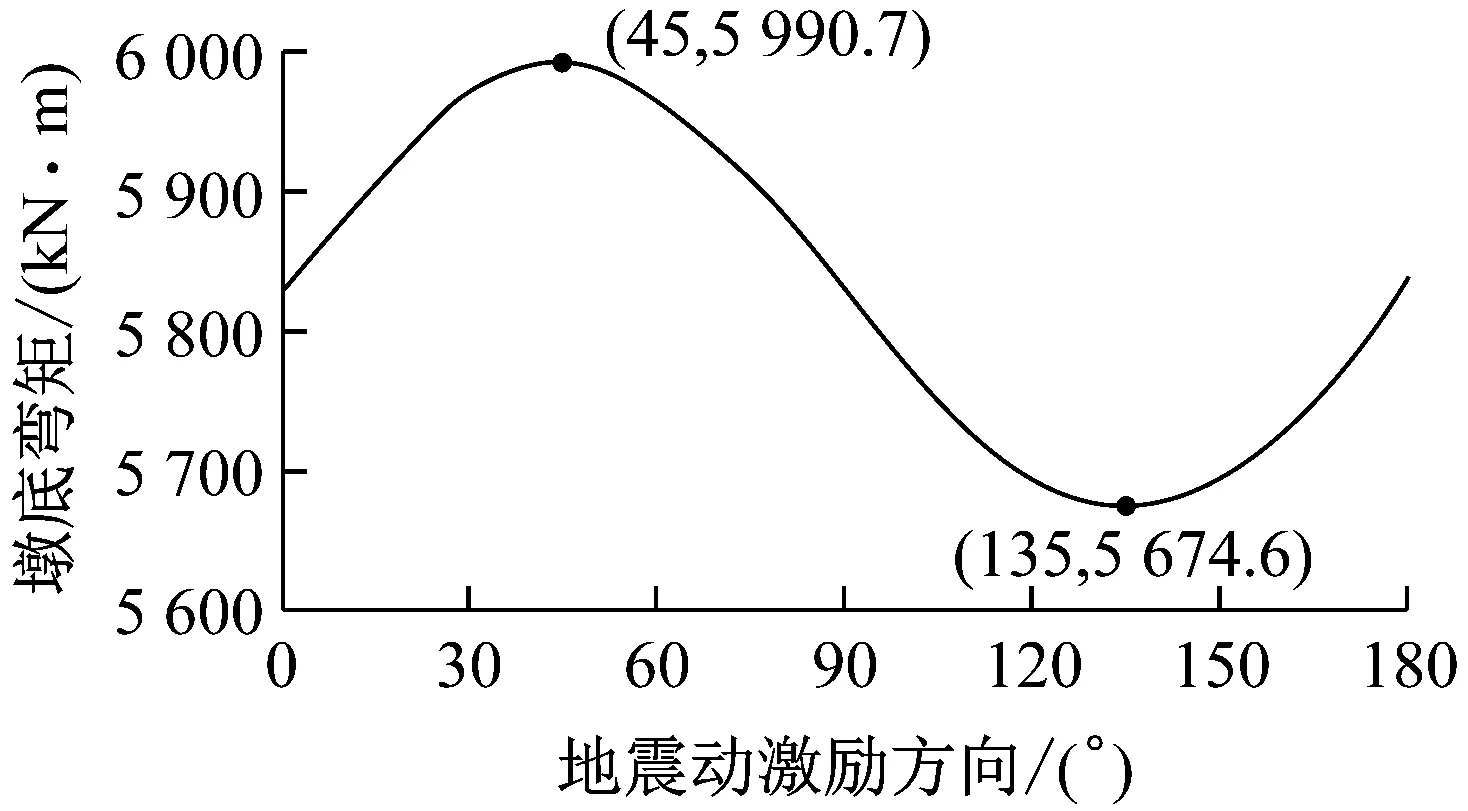
a 墩底弯矩

b 支座位移
图6描述了地震动沿不同方向激励时构件截面各方向响应峰值,由图可知,对于桥墩而言,α=128°为墩底截面弯矩响应最大方向,而α=159°为支座位移响应最大方向.对于部分采用圆形截面的构件而言,由于其各方向力学性质相同,即截面能力相同,截面响应最大处就是最不利受力部位,由此可知通过构件合力法能够捕捉部分构件截面最不利受力部位,为实际工程的抗震设计及加固提供参考.

a 墩底弯矩
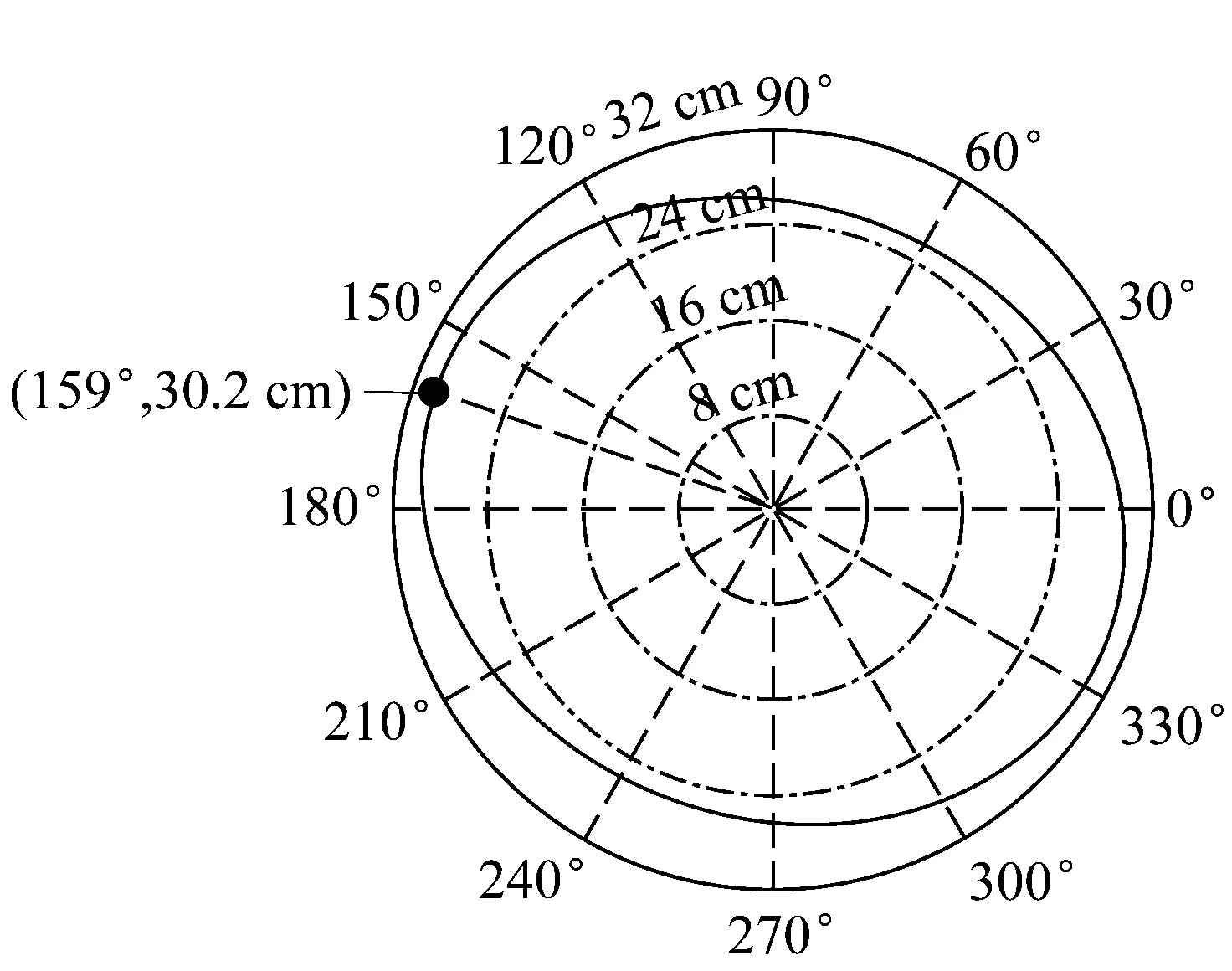
b 支座位移
另一方面,图7中是Northridge(Rinaldi)地震作用时不同激励方向下构件局部坐标轴方向响应分量峰值,从图中可以看出不同局部坐标轴方向的响应分量所对应的最不利激励方向不同,并且地震动沿其各自的最不利激励方向作用时所产生的响应峰值也不同.以墩底弯矩为例,如图7a所示,绕局部2轴方向的弯矩峰值为5 745.1 kN·m,其对应的最不利输入方向为θ=90°,而绕局部3轴方向的弯矩峰值为5 831.7 kN·m,其对应的最不利输入方向为θ=15°,因此,很难通过局部坐标轴方向响应分量来确定该桥墩的最不利激励方向.同时由于局部坐标轴方向响应峰值的不同,若采用任一响应分量的峰值来确定结构最不利激励方向,很有可能低估结构的地震响应,影响结构抗震设计的安全.
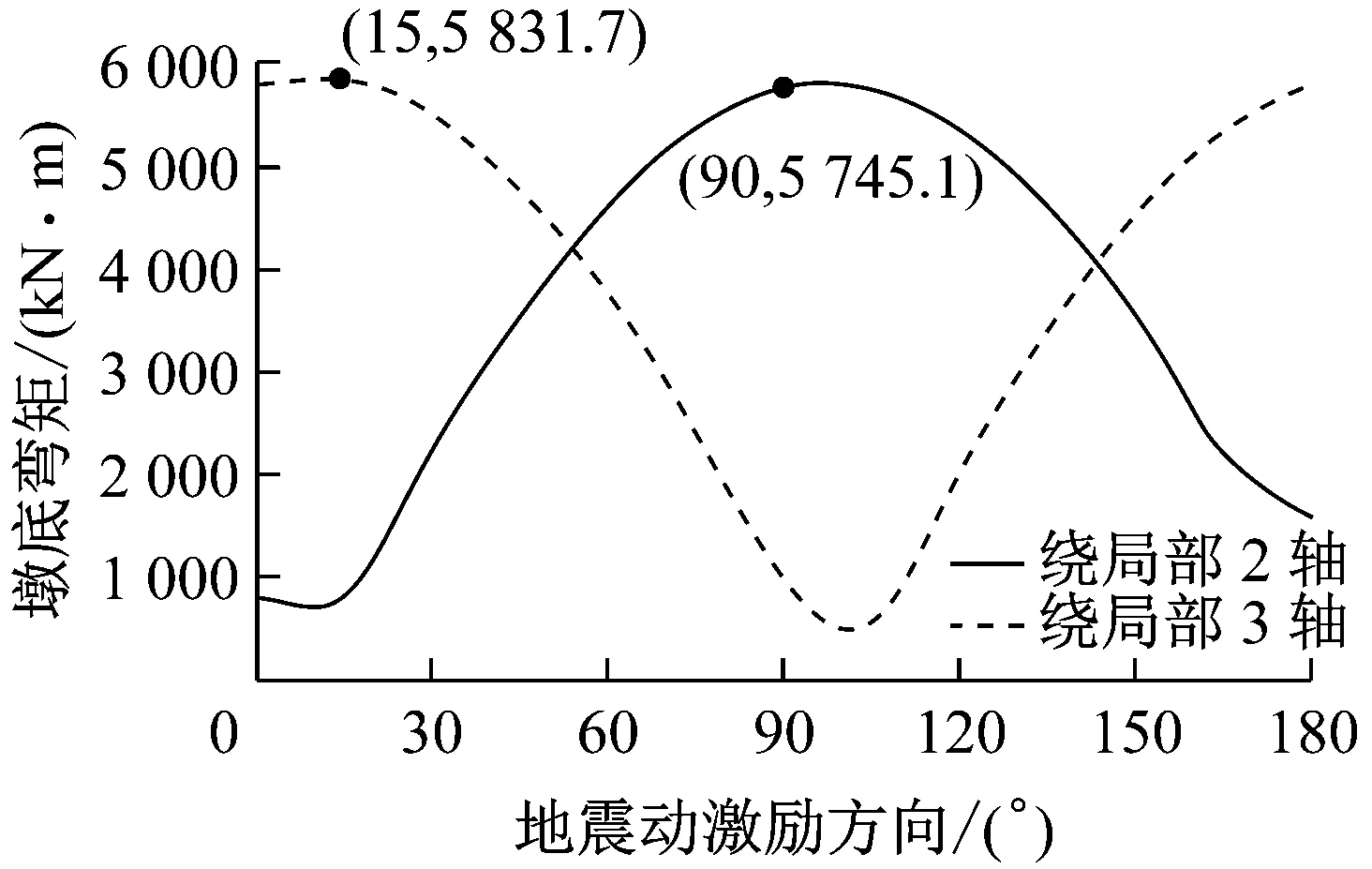
a 墩底弯矩

b 支座位移
4 构件合力法与全角度输入法计算结果比较
采用全角度输入法,分别输入3条地震波,在各个方向对曲线桥进行线性时程分析并与构件合力法所得计算结果进行比较,地震动输入角度间隔为15°.
图8为不同激励方向下2种计算方法的比较结果.由图可知,在3条地震波作用下2种分析方法所得结构的地震响应峰值随激励方向的变化趋势一致,计算得到的最不利激励方向均为θ=45°且各激励方向下的地震响应峰值相差最多不超过4%,从而反映出构件合力法在确定结构最不利激励方向时具有较高的可靠性,并且构件合力法仅需分别沿X、Y方向对结构进行2次反应谱分析便可确定结构的最不利激励方向,相对于全角度输入法而言(本算例进行了13次时程分析)计算量更小、更为高效.此外,图8中还描述了根据规范方法[15](图9)确定的曲线梁桥地震动最不利激励方向及相应的响应值.由图可知,采用规范方法得到的最不利激励方向与构件合力法及时程方法所得最不利输入方向相差26°且采用规范方法得到的结构的响应偏小,与时程方法相比,最不利激励方向下构件响应值最大相差3.5%(图8d),从而表明当以构件合力作为最不利输入方向的判别标准时,尽管规范方法可能造成对于结构构件响应的低估,但与理论方法相比相差较小,能够满足实际工程抗震设计的需要.由于3条地震动频谱特性各不相同,而由图可知,各条地震动作用下该桥最不利激励方向基本相同,说明地震动频谱特性对于该桥的最不利输入方向影响较小.
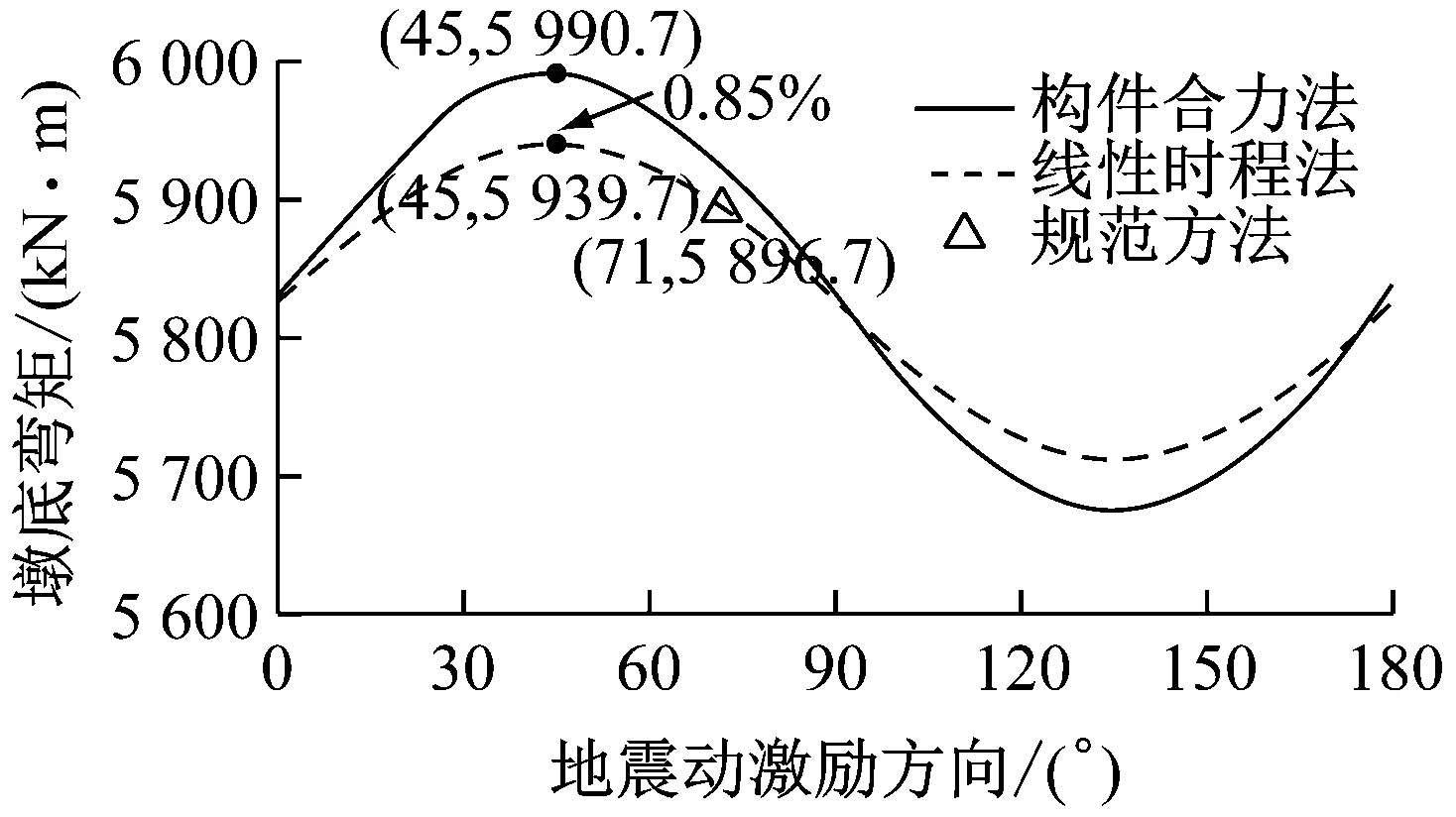
a Northridge(Rinaldi)地震作用下墎底弯矩

b Northridge(Rinaldi)地震作用下支座位移
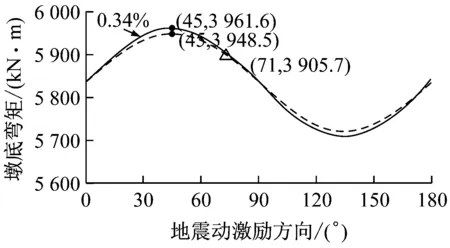
c Northridge(Santa Monica City Hall)地震作用下墎底弯矩
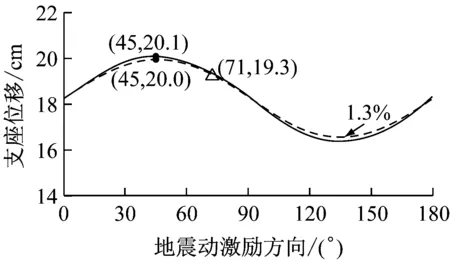
d Northridge(Santa Monica City Hall)地震作用下支座位移
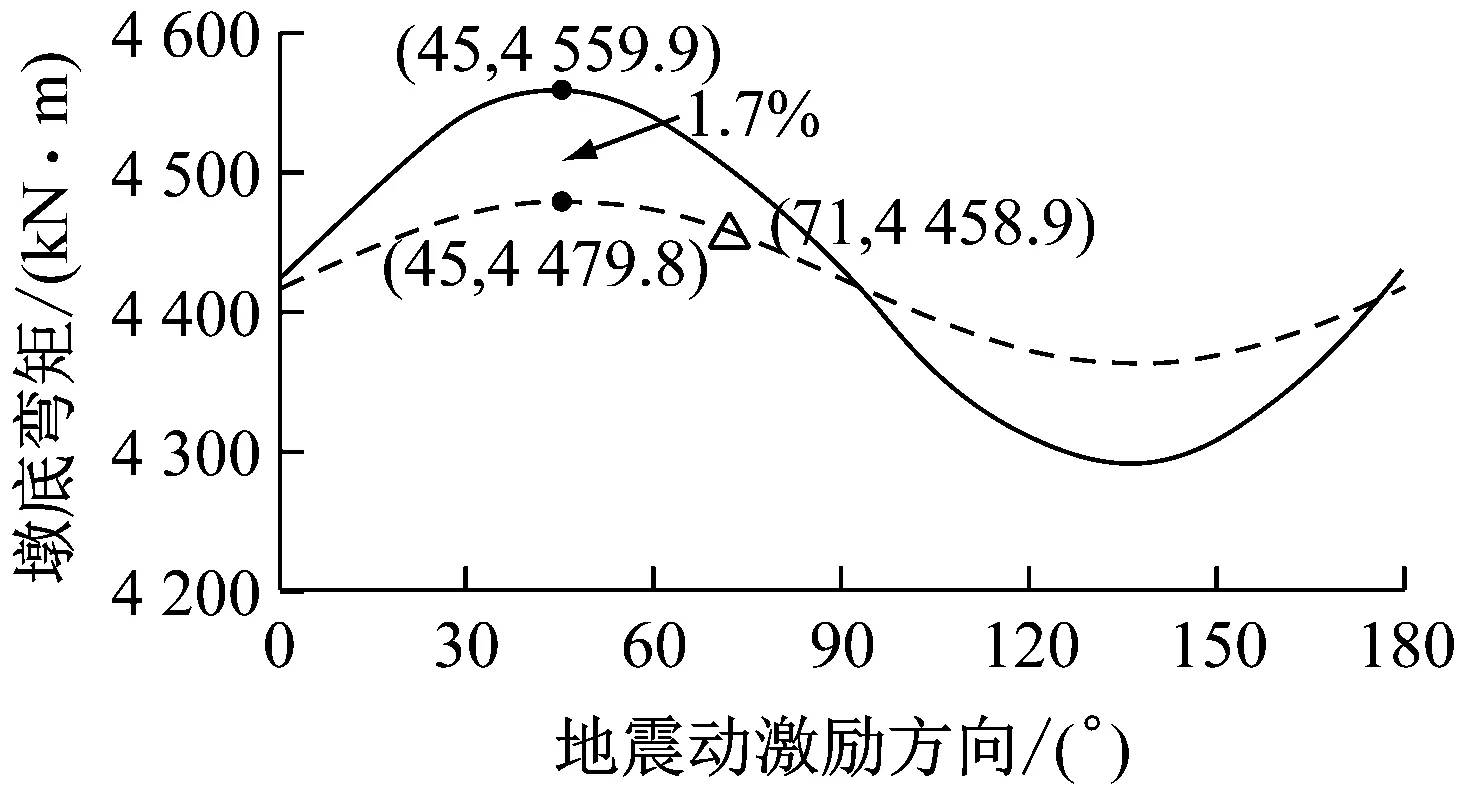
e Loma Prieta地震作用下墎底弯矩
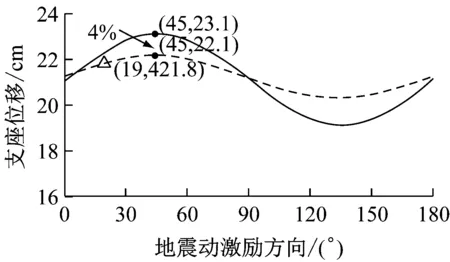
f Loma Prieta地震作用下支座位移

图9 现行规范规定的曲线桥地震输入方向
5 结论
(1) 对于任何结构,构件合力法只需在其纵、横向进行2次反应谱分析,再通过编制计算程序进行极值分析,便可求得结构的最不利激励方向,相比于全角度输入法(本文算例共进行13次时程分析)计算量更小,对于确定复杂结构的最不利激励方向更加省时.
(2) 构件合力法具有较高的计算精度.针对算例桥梁,构件合力法与全角度输入法计算得到的最不利激励方向相同且地震峰值响应相差最多不超过4%.应用构件合力法能够确定圆形截面桥梁构件的最不利受力部位,可以为实际工程的抗震设计及加固提供参考.
(3) 对于算例桥梁,3条地震波作用下构件合力法与全角度时程分析方法得到的最不利激励方向均为θ=45°;采用规范方法得到结构的最不利激励方向为与构件合力法及时程方法相差26°,但在最不利激励方向下构件响应峰值与时程方法最大相差3.5%,表明按照现行规范规定的地震动激励方向对曲线梁桥进行抗震性能验算能够满足实际工程抗震设计的需要.
(4) 曲线梁桥不同构件的地震响应对地震动激励方向的敏感性有所不同;对于算例桥梁,Northridge(Rinaldi)地震沿不同方向激励时墩底弯矩峰值最大仅相差5.3%,而不同激励方向下支座位移峰值最大相差15.2%.
(5) 地震动频谱特性对该曲线梁桥最不利激励方向的影响较小,在3条不同频谱特性的地震动输入下,该桥的最不利激励方向基本不变.

