基于直方统计特征的多特征组合航迹关联

徐亚圣 丁赤飚 任文娟 许光銮

①(中国科学院大学 北京 100049)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

④(微波成像技术重点实验室 北京 100190)

1 引言

数据融合目前在各个领域有着广泛地应用[1，2]，分布式多传感器融合系统是一种典型的多传感器数据融合系统[3，4]，具有鲁棒性强、成本低的特点。航迹关联方法的研究一直是分布式多传感器融合系统中的一个热点。航迹关联就是确认多条来自不同传感器的目标轨迹是否属于同一目标，关联后可以有效地降低数据的冗余，正确的关联也是实现数据融合的前提。目前航迹关联的方法可以分为两大类，一类是基于统计的方法，另一类是基于模糊数学的方法。基于统计的方法主要是利用状态估计的差作为统计量并建立统计假设，然后以设定的概率阈值来判定航迹是否关联[4-6]。基于模糊数学的方法主要是选定或设计关联隶属度，通过计算两两航迹的关联隶属度来判断航迹是否关联[6-8]。这些方法主要存在以下问题：(1)对目标的航迹进行逐点比较，没有从航迹整体的角度来考虑，忽视了航迹的全局性的特征；(2)基于统计的方法需要人工设定阈值和大量的调试，扩展性不强；(3)只考虑了随机误差，而忽视了其他误差的影响。

针对上述问题，大量文献对其进行了研究。文献[9]将航迹的整体视为时间序列，使用动态时间规整(Dynamic Time Warping， DTW)来测量任意两条航迹之间的相似度，从整体上考虑了航迹形状的相似性。将DTW相似性引入航迹关联当中，避免了在时域上进行配准，在一定程度上减小了误差。文献[10]将系统误差引入到原始的传感器量测中，构建了一种混合整数非线性规划模型，并对系统误差进行了估计，有效地提高了系统的性能。文献[11]提出了一种具有自适应阈值的最大后验概率(Maximum A Posteriori probability， MAP)关联算法。该算法显示，具有自适应阈值的算法性能优于固定阈值算法。

针对现有方法存在的需要人工设定阈值、参数设置复杂、只考虑单个航迹点以及航迹信息利用不充分的问题，本文提出了一种基于多特征组合的航迹关联方法。首先从航迹的整体出发，在传统欧式距离度量的基础上，提出了一种距离分布直方图的特征并提取了航迹的相似特征，有效地利用了航迹整体的特性，具有较好的抗噪声性能以及关联准确率。其次挖掘了航迹间的速度差分布直方图特征、传感器来源特征，然后将这些特征组合，考虑到目前机器学习方法强大的特征学习能力，能够自动地学习特征中隐含的知识信息，且参数设置较为简单，因此利用机器学习方法对挖掘的特征进行学习得到航迹关联模型，从而有效地避免了需要人工设定阈值以及参数设置复杂的问题。最后通过实验验证了本文方法的有效性。

2 系统模型描述

船舶的航迹由一系列时空数据点(即经度、纬度、时间)组成，并且通过多种定位方式获得，由于同一个目标可能会被多个源观测到，因此在数据融合中心会出现一个目标的多条航迹观测(对于多条观测的情况，我们可以对观测中的航迹两两进行关联判断，最后得到关联结果)，在系统中造成大量的数据冗余，在未判明目标时则会造成大量虚假目标信息，对后续的一些航迹知识挖掘任务，如目标识别、航迹融合造成很大的影响。

假设分布式多传感系统中有M个传感器，每个传感器输出的航迹数为ms，将其中任意一条的航迹数据即目标的状态估计表示为sk，其中s=1,2,3,⋅⋅⋅,M,k=1,2,3,⋅⋅⋅,ms。目 标 的 状 态估计sk可以表示成为时间序列(1维或者多维的)，这里定义sk为如下的一个多维的时间序列：

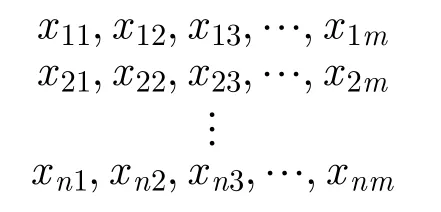
其中，m表示航迹的长度，n表示属性的维数。对于任意的两条航迹数据(经过一定预处理后，在同一时间段里的两条航迹数据)存在以下两种假设H0和H1：

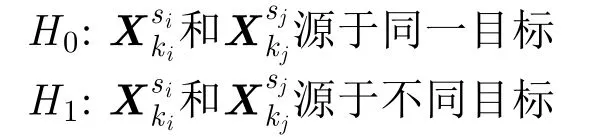
3 算法描述

3.1 特征挖掘

3.1.1 距离分布直方图特征

距离是航迹间最基础也是最直观的特征，传统的航迹间的距离特征有欧式距离、编辑距离以及其它描述航迹形状相似度的距离等，传统的欧式距离主要是计算航迹对应的距离和或者最大最小距离[12]，且需要两条航迹在时间上对齐，这些特征虽然简单且能在一定程度上解决关联的问题，但也有着十分明显的缺点：(1)单一数值不能很好地反映航迹间的细节差异；(2)在关联时需要人工设定阈值，依赖于人工经验，且关联准确率敏感于噪声。

针对上述存在的问题，本文在欧式距离算法的基础上，提出了一种基于距离分布直方图特征(图1)。特征描述如下：

经过一定预处理(按照4.1.2节中，第1部分所做的时间对齐和抽样。3.1.2节及3.1.3节的特征提取也经过这样的预处理)，两条时间上对齐(采样点的时间相同)、航迹长度相同、特征维度为经度、纬度、时间的航迹

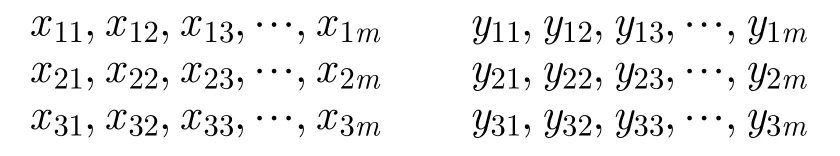
其中，m表示航迹的长度，设航迹的距离序列为

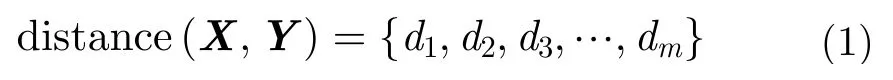
其中，di表示 和 第i个航迹点对应的距离。为了规范化处理，本文对距离序列 d istance取对数，得到：

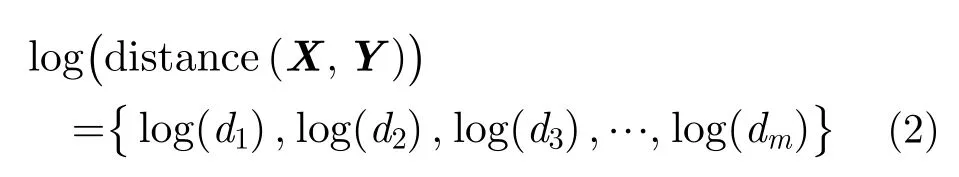
3.1.2 动态时间规整(DTW)相似度特征

航迹作为一种时间序列，可以考虑将其相似度作为一种特征，而DTW是一种典型的用于计算时间序列相似度的算法，它广泛应用于科学、医学、工业、金融等领域，在人工智能领域使用得更为频繁[13-22]。DTW定义了时间序列间的最佳匹配，它同时支持不同时间长度的相似度量，具有更好的鲁棒性。DTW也从一定程度上反映了航迹间的形状相似度。因此本文计算航迹间的DTW相似度，并将其作为一类特征。同上设有两条航迹长度分别为m,n且m,n＞1。特征维度为经度、纬度、时间的航迹

我们构建一个m×n的矩阵其中，dij为d(xi,yj)，是两条航迹两个点xi和yj的距离。本文将距离定义为两个经纬度点的实际距离，因此矩阵中的每个元素(i,j)表示的是两个点的匹配程度。在矩阵中构建一条路径表示航迹和的匹配程度：

图1 距离分布直方图特征计算示意图Fig.1 Schematic diagram of feature calculation of distance distribution histogram

路径 必须满足以下3个条件：

(1) 边界条件：w1=(1,1),wk=(m,n)；

(2) 连续条件：给定wp=(ip,jp),wp+1=(ip+1,jp+1)，有ip+1-ip≤1,jp+1-jp≤1；

(3) 单调条件：给定wp=(ip,jp),wp+1=(ip+1,jp+1)，有ip+1-ip≥0,jp+1-jp≥0。

其中有多条路径满足上述的条件，取满足以下条件的路径：

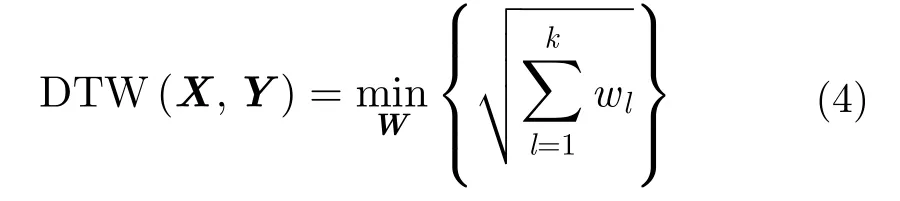
为了计算式(4)，需要构建一个累加距离矩阵，并且利用动态规划的思想求解这个矩阵，递归如下：

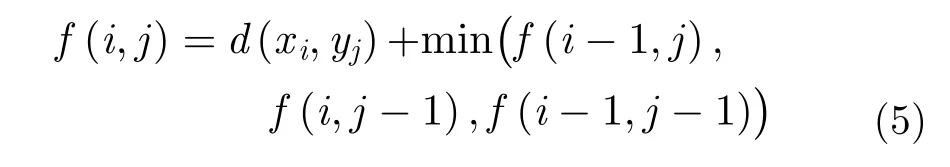
初始条件为

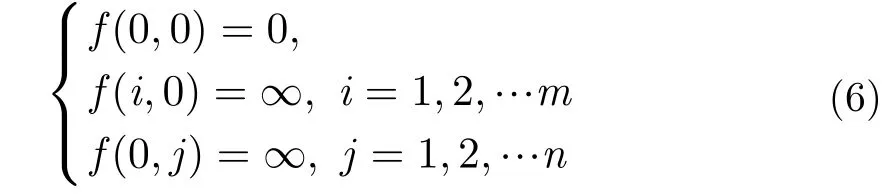
最终得到的f(m,n)为航迹的DTW特征。图2及图3显示了两条航迹在DTW算法下的逐点对应关系。

3.1.3 其他特征

航迹间除了距离和DTW相似度两种主要特征外，本文还提取了速度差分布直方图特征以及航迹的来源特征，考虑到船舶的行驶速度较慢且传感器的采样频率较高，本文假设任意两个航迹点之间，船做的是匀速直线运动，从而可以得到每一个航迹点的速度，对于航迹 和，记航迹 和 的速度序列为

图2 DTW航迹点对应关系Fig.2 Correspondence of DTW track points

图3 DTW算法匹配关系Fig.3 DTW algorithm matching relationship

其中：

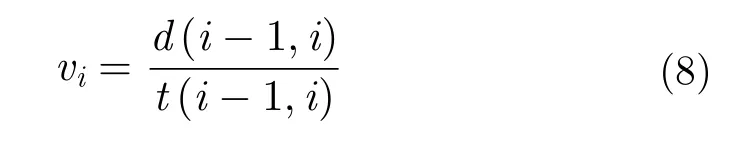
d(i-1,i) 表示的是第i个点与i-1个点的距离，t(i-1,i) 表示的是第i个点与i-1个点的时间差。

设：

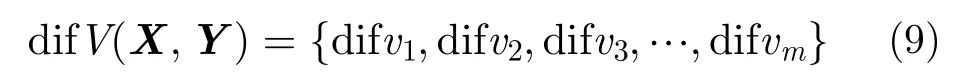
为航迹X和Y的速度差序列，其中difvi表示 和第i个航迹点对应的速度的差。然后对做与d istance相同的后续处理得到速度差分布直方图特征。

不同来源误差往往不同，传统的一些方法在进行仿真实验的时候假定误差服从高斯分布，而实际的误差情况不仅有随机误差还有系统误差的影响，同时不同来源的精度、特性也不相同，因此本文将不同数据来源量化为特征，结合机器学习的方法隐性地学习误差信息从而在一定程度上更好地克服误差影响。假设有n个不同的来源：

本文将其进行一定的编码作为来源特征

3.2 关联流程

对任意两条航迹数据提取距离、速度差分布直方图特征、DTW相似度特征以及来源特征，并将这些特征进行组合。然后利用机器学习的模型来进行训练和判断。算法的流程图如图4所示。

4 实验验证

4.1 实验数据集构建及预处理

4.1.1 数据集构建

传统的一些方法实验都是仿真数据上进行的，虽然为了接近真实的情况，在仿真数据上加入了噪声等干扰，但大多数都是假定噪声服从高斯分布，忽视其他误差的影响，因此与实际的船舶航迹数据仍然有着较大的差距。本文构建了一个真实的船舶航迹数据集，船舶航迹数据集是1年多的船舶航迹数据，涵盖了较多的航迹运动情况，数据集中每一个实验样本由两条航迹组成，两条航迹可能源于同一目标，也可能源于不同的目标。数据集的航迹样本标注都是经过一定的历史分析以及多个有经验的判读员检验标注的。因此数据集的标注具有较高的可靠性。本文一共标注了8063个航迹实验样本对，令两条航迹源于同一目标的为正样本，两条航迹源于不同目标的为负样本。其中正样本数量为2522个、负样本为5541个。

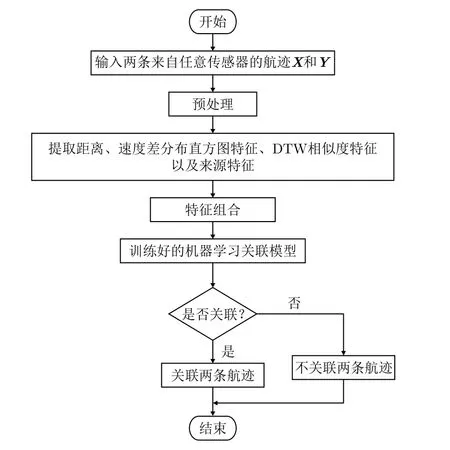
图4 关联流程图Fig.4 Association flow chart

4.1.2 数据预处理

(1) 时间对齐和抽样

一般情况下，各个传感器采样频率上报间隔都不尽相同，因此会出现如图5所示的情形。不同传感器的采样频率往往不同，得到的航迹点的时间并不一一对应，如果直接计算距离会有较大的误差，且不满足计算距离分布直方图特征的条件，因此需要对航迹进行插值，再在同一时刻进行采样。

通过对航迹数据集中的数据(在本文构建的数据集里)进行分析后，发现传感器的采样频率大多数在3～300 s，船舶行驶速率大多在11节左右(20 km/h)。因此本文假设船舶的两个采样点之间是做匀速直线运动，从而进行线性插值处理，此假设主要是为了减小直接计算非时间对齐航迹点的欧式距离时的较大误差同时满足距离分布直方图特征的计算条件。线性插值采样如图6所示。同时为了更符合匀速直线运动的假设，本文将不对采样间隔大于600 s的点做插值处理。

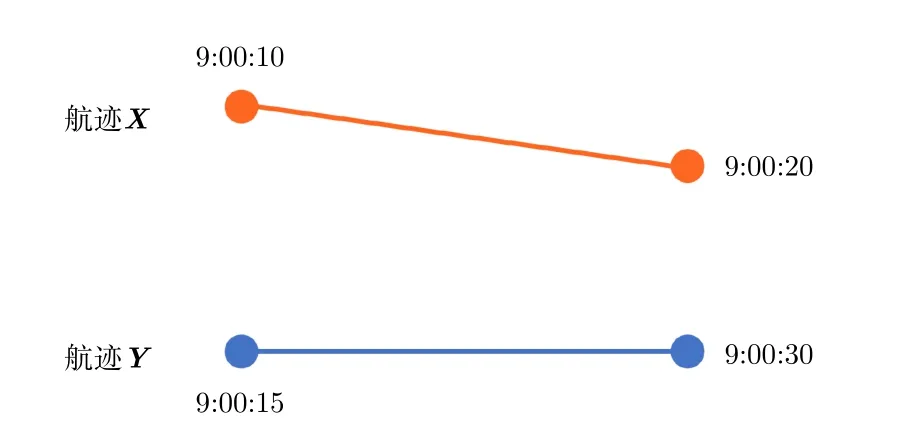
图5 两条航迹对应点时间不同示意图Fig.5 Different timings of the corresponding points on the two tracks

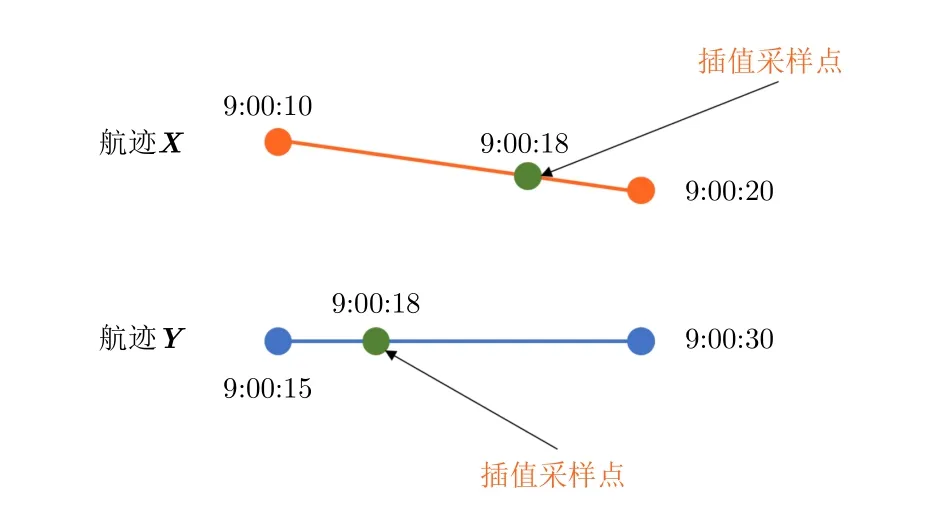
图6 航迹线性插值采样示意图Fig.6 Linear interpolation sampling schematic diagram

(2) 样本扩充

原始的可用样本较少，正样本数量仅为2522个、负样本为5541个，通过对样本的观察发现：部分样本的时间跨度较长且样本点数极多(例如有些样本航迹点数有3万多个，时间长度超过20 h)。这样的样本可以对其进行拆分，拆分方式如图7所示，本文将其拆分为时间长度为2～3 h的多个样本以此来扩充样本。

图7 航迹样本拆分示意图Fig.7 Schematic diagram of separation of track samples

4.2 实验结果分析

为了验证算法的性能，本文首先比较了传统方法提取的加权距离特征(加权航迹方法计算出的统计量特征)[23，24]、平均距离特征、最大距离特征在设定阈值与利用机器学习方法时性能的差异，其次比较了距离分布直方特征与传统的平均距离特征、加权航迹特征、最大距离特征，之后对本文提出特征进行组合，比较组合特征和单一特征的性能，最后对比了不同的机器学习方法的性能。实验数据集是经上述预处理后并随机打乱后的船舶样本集，其中80%的样本用来训练，20%的样本用来测试。

4.2.1 评价指标

本文采用常用的机器学习评价指标[25]，精度、查全率、查准率、F1度量、ROC (Receiver Operating Characteristic)曲线以及AUC (Area Under Curve)值，令两条航迹源于同一目标的为正样本，两条航迹源于不同目标的为负样本。则评价指标的具体定义如下：

ROC曲线根据学习器的预测结果对样本进行排序，并且按照这个顺序把样本预测为正例，性能越好的模型，ROC曲线越接近于左上角。由于从图形上无法直观比较ROC曲线，因此可以通过计算ROC曲线下方的面积，即AUC值，来比较模型的好坏，一般来说AUC值越大则表示模型性能越好。

产业结构的区域差异性是制约我国经济发展的重要因素，学术界关于我国产业结构区域特征的研究由来已久。中国产业结构的确存在区域差异性（Naughton，2003），但这种差异性在趋同作用下逐渐衰减且呈收敛特征（Poncet，2003）。三大产业的发展成本有所不同，其中第三产业的发展能降低加工成本和交易成本，有利于提高社会整体的经济效率（吴敬琏，2014）。

表1 平均距离特征阈值方法与机器学习方法指标对比Tab.1 Comparison of average distance characteristics threshold method and machine learning method index

表2 加权距离特征阈值方法与机器学习方法指标对比Tab.2 Comparison of weighted distance characteristics threshold method and machine learning method index

表3 最大距离特征阈值方法与机器学习方法指标对比Tab.3 Comparison of maximum distance characteristics threshold method and machine learning method index

4.2.2 阈值方法与机器学习方法对比实验

传统的方法阈值设置大多根据统计以及设计者经验来决定[26]，其中一些方法还依赖于系统的参数[4，27]，本文根据真实数据集的情况，利用了3种数据的统计值作为阈值来与机器学习方法进行比较，它们分别是精度最高阈值、平均数阈值以及中位数阈值。精度最高阈值：也是一般常用的阈值设置方法[4]，在特征域值范围内的值，通过一定的步长设置寻找最佳精度阈值；平均数阈值和中位数阈值主要是利用特征的统计特性[28]，本文对3种特征分别求得它们平均数与中位数作为阈值，具体的阈值与实验结果如表1～表3所示。机器学习模型则选较为常用的树模型，从表1～表3中可以看出，机器学习的方法则能够更好学习特征表示的含义，具有更强的泛化能力，因此关键指标均远高于设定阈值的方法，且不需要人工设定阈值(精度最高阈值需要大量的实验才能确定)，进而说明了引入机器学习方法的有效性。

4.2.3 距离分布直方图特征与传统特征对比实验

表4是利用树模型学习不同特征的各项指标，图8描述了不同特征的ROC曲线图。从表4以及图8可以看出本文提出的距离分布直方图特征的性能优于传统的距离特征。主要原因是距离分布直方图特征从航迹的整体出发，更好地考虑了整体的距离分布。图9是传统距离特征无法识别而距离分布直方图特征能识别的关联目标，图中红色和蓝色分别代表了不同来源观测的同一目标的航迹。从图中可以看出，传统的距离特征由于是单一数值描述，对有噪声干扰的目标不能准确关联，而距离分布直方图特征考虑的是整体的距离分布，因此具有较好的抗噪性能。图10是距离分布直方图特征关联失败的典型情况，图10(a)和图10(b)是两条航迹源于同一目标，图10(c)为两条航迹源于不同目标。从图10(a)和图10(b)中可以直观地看出，其受噪声干扰较为严重，而图10(c)两条航迹十分接近，通过对它们特征的可视化分析发现，图10(a)、图10(b)距离整体分布呈现较大差异，此时距离分布直方图特征难以有效地关联图10(a)、图10(b)所示的情况。图10(c)的距离整体分布十分接近，但速度整体分布差异较大，单一的距离分布直方图特征在这种情况难以正确完成关联判断。

表4 不同特征指标对比Tab.4 Comparison of different characteristics

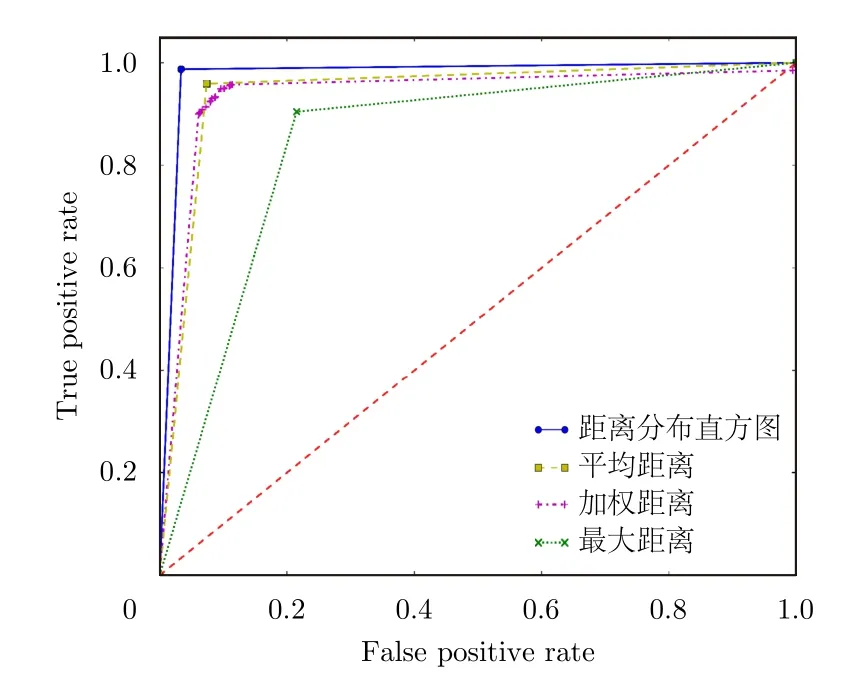
图8 不同方法ROC曲线Fig.8 Different methods of ROC curves

图9 传统距离特征无法识别而距离分布直方图能够识别的目标Fig.9 The targets that can’t be identified by traditional distance feature but can be identified by distance distribution histogram

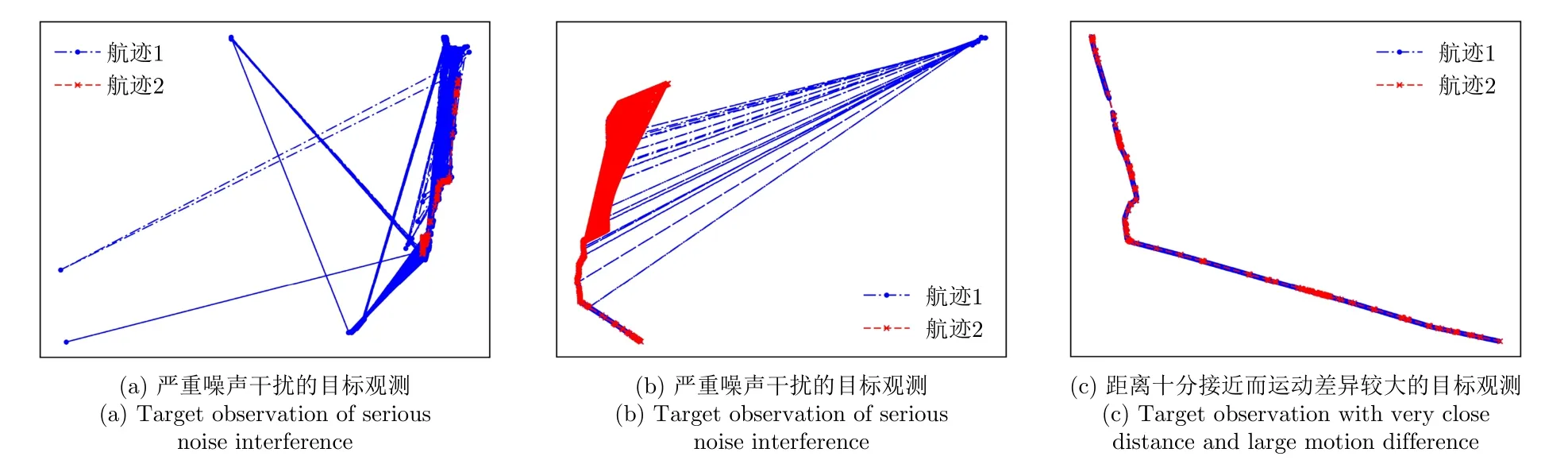
图10 距离分布直方图特征关联失败的目标Fig.10 The targets of distance distribution histogram feature error association

表5 组合特征指标对比Tab.5 Comparison of composite features

图11 特征组合ROC曲线Fig.11 Feature combination ROC curve

4.2.4 组合特征对比实验

表5是利用树模型学习不同组合特征的各项指标，图11描述了不同组合特征的ROC曲线图，表5以及图11中，DDH (Distance Distribution Histogram)表示的是距离分布直方图特征，SDDH (Speed Difference Distribution Histogram)表示的速度差分布直方图特征。图12给出了单一特征错误关联而组合特征正确识别情况(图10(c)在加入速度差分布直方图特征后能够准确地判断其为不同的目标)，图12(a)是DDH特征错误关联的目标而加入DTW相似度特征准确识别的情形，主要原因是两条航迹的距离较近，在距离维度上很难区分，而其DTW相似度差异较大(DTW相似度在一定程度上描述了航迹形状上的相似度)。图12(b)是DDH+DTW特征错误关联的目标而加入速度差分布直方图特征准确识别的情形，主要原因是两条航迹的距离较近，DTW相似度也较高，而其有12.5%的航迹点速度相差5节航速，速度差分布差异较大。图12(c)是DDH+DTW+SDDH特征错误关联而加入来源特征准确识别的情形，主要原因是两条航迹的距离较近，DTW相似度也高，速度差分布也相近，但两条航迹来自同一观测源，因此判定不是同一目标。图13是距离分布直方图特征关联失败的典型情况，图13(a)和图13(b)是两条航迹源于同一目标，图13(c)为两条航迹源于不同目标。从图13(a)、图13(b)中可以直观地看出，其受噪声干扰较为严重，而图13(c)两条航迹十分接近，通过对它们特征的可视化分析发现，图13(a)和图13(b)的距离、速度整体分布以及DTW相似度呈现较大差异，此时组合特征难以有效地关联图13(a)和图13(b)所示的情况。图13(c)的目标十分接近，且几乎没有移动，因此各项特征十分接近，组合特征在这种情况难以正确完成关联判断。综上分析以及从表5和图11中可以看出，每增加一组特征，模型的各项指标都有所提升，不仅说明了所提特征的有效性，而且由于不同特征之间具有一定的互补性，多种特征的组合能够更加全面地表征航迹间的关系，进一步提升航迹关联准确性。在噪声干扰较大时航迹间的特征也受到了较大的干扰，此时很难有效地进行关联判定，同时由于目前航迹点信息有限，可以挖掘的特征有限，因此在一些较为特殊的情况下当前组合特征不能准确地完成关联判断。

4.2.5 不同机器学习方法对比实验

图13 组合特征关联失败的目标Fig.13 The targets of combination features error association

表6 不同机器学习方法指标对比Tab.6 Comparison of different machine learning indicators

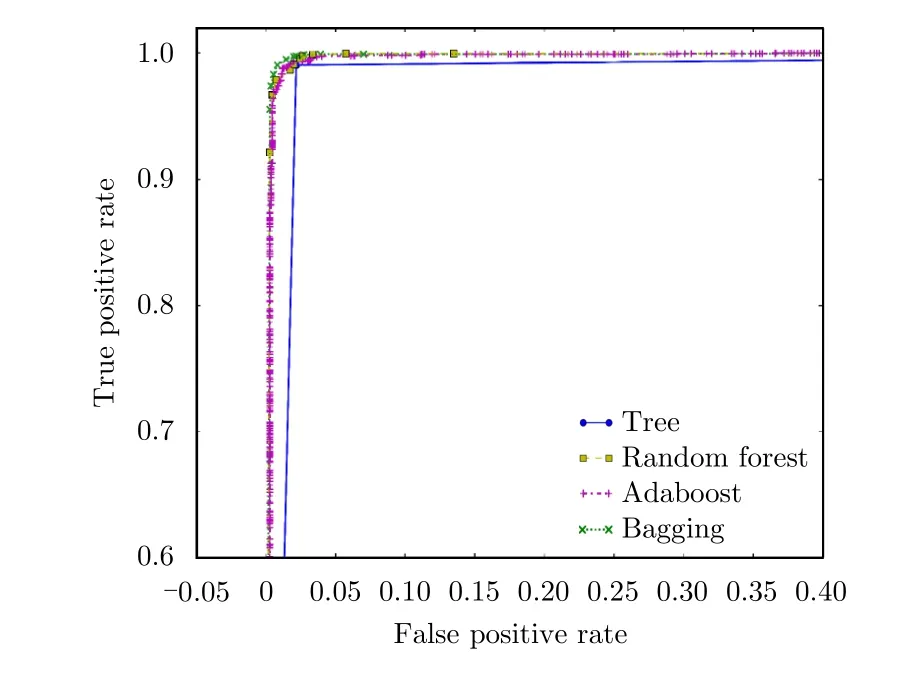
图14 不同机器学习方法ROC曲线Fig.14 ROC curves for different machine learning methods

5 结论

针对传统航迹关联方法存在需要人工设定阈值、参数设置复杂的问题，本文将机器学习的方法引入航迹关联中，针对一些传统方法只考虑航迹单个点的信息及抗噪声性能较差的问题，本文从航迹的整体出发，提出了一种距离分布直方图特征。与此同时对航迹的特征进行挖掘，提取了航迹间的DTW相似度特征、速度差分布直方图特征以及来源特征，结合机器学习的方法提出了一种基于多特征组合的航迹关联方法，该方法在有限的航迹点信息中挖掘了多种有效的特征信息，获得了较高的关联准确率，并且在实际应用中取得较好的效果，随着样本和航迹点信息不断增多，关联模型的准确率以及泛化性能还将进一步提升。理论分析和实验结果均表明该方法的有效性和合理性。根据算法设计中各环节的假设和约束，本文目前提出的航迹关联算法主要适用于传感器采样频率较高，运动目标速度较慢(船舶、汽车、行人等)的情况，对于高速运动的目标则需要进一步地分析其运动情况，建立更加精细的插值模型，这也是本文后续工作中的一个重要的研究方面。