基于权重归一化奇异值分解的辐射源信号识别研究
苑 霸 姚 萍 郑天垚)
①(中国科学院计算技术研究所 北京 100190)
②(中国科学院大学 北京 100049)
1 引言
辐射源信号识别研究在雷达电子战或软件定义无线电的数字接收机中广泛应用,一直以来都受到广泛关注。现阶段的辐射源信号识别算法所遵循原则可以分为两类:决策理论和模式识别。基于决策理论的算法主要立足于假设论证及概率论,例如文献[1-4]均依赖于极大似然准则进行识别算法设计,文献[5-7]则很好地利用概率统计原则进行信号识别。但上述两种原则分别存在计算复杂度高、阈值确定困难的问题。
随着计算机软硬件发展及模式识别算法的不断成熟,基于模式识别理论的信号识别算法取得长足进步。模式识别算法一般由数据预处理、特征提取、特征选择及模型构建4个模块构成,而现有的算法主要从特征提取与分类模型构建两个模块入手进行。多数算法在特征提取过程中主要立足于信号的统计特征、变换特征及信号瞬时振幅、相位、频率等相关理论。例如文献[8,9]根据信号随机过程理论提出信号高阶累积量的特征提取方法;文献[10-12]在进行特征提取时主要从信号的时频特征出发,而文献[10,13]则引入小波变换特征作为其重要的识别特征。上述方法虽然在对辐射源信号分析识别中取得一定效果,但是在低信噪比条件下的表现不甚理想。
本文的主要贡献在于提出一种与上述方法切入点完全不同的特征提取方法。该方法从信号能量出发,基于权重归一化奇异值分解方法提取辐射源信号特征,在保留信号主要能量基础上,进行信号噪声滤除、特征提取及特征选择,实现不同信号间特征差异极大化,完成信号的正确识别与分离。
近年来,随着机器学习相关理论的不断发展,越来越多分类算法引入到信号识别中,例如文献[9,13,14]中使用支持向量机作为信号分类器;文献[15,16]采用人工神经网络进行信号识别,文献[17]采用受限玻尔兹曼机作为其分类模型。本文引入随机森林、K近邻法、朴素贝叶斯算法及逻辑回归4种模型构建信号分类器,对特征提取算法进行识别效果及鲁棒性分析。
仿真实验结果表明,基于权重归一化奇异值分解的特征提取算法对辐射源信号的调制类型识别具有良好的识别效果,且在低信噪比条件下仍然表现优秀,具有较好的鲁棒性。
本文内容组织如下。第1节为引言,第2节详细描述本文提出的基于权重归一化奇异值分解的信号特征提取算法,第3节进行典型雷达信号数据仿真,第4节对基于权重归一化奇异值分解算法的滤波效果进行分析,第5节进行数据矩阵的行数对奇异值分解结果的影响分析,第6节对算法识别效果进行分析,第7节总结论文研究工作及下一步工作方向。
2 权重归一化奇异值分解算法
2.1 数据预处理
在进行模式识别时,首先必须对原始数据进行预处理。本文中处理的信号为雷达脉冲信号,在使用奇异值分解进行特征提取时,需要构建原始数据矩阵。文中采用简单截断的方式,将接收的脉冲信号数据整理为等长的数据,然后将每个脉冲信号数据作为矩阵的一行,组成M×N阶的原始数据A。
此外由于接收信号的幅值可能因为距离、噪声及收集设备功率的影响而各不相同。为避免脉冲信号因为幅值不同而对特征提取带来影响,在进行特征提取前需对每个脉冲数据进行归一化。归一化方法如下所示:

2.2 基于奇异值分解的特征选择
2.2.1 奇异值分解基本原理
奇异值分解是线性代数中重要的矩阵分解方法之一,在信号处理、统计学等领域广泛应用。例如文献[18]使用奇异值分解进行音频信号去模糊,文献[19,20]利用奇异值分解进行图像去噪。此外奇异值分解可以用于信号压缩,例如文献[21]中使用奇异值分解进行了信号压缩。奇异值分解与另外一种在机器学习领域广泛应用的矩阵分解-特征值分解关系密切。两者的目的都是提取矩阵最重要的特征,但奇异值分解比特征值分解更具有普适性,特征值分解只能应用于方阵,奇异值分解可以适用于任何矩阵。
假设A是一个M×N阶矩阵,其中的元素全部属于域K,K为实数域或复数域。如此则存在一个分解使得

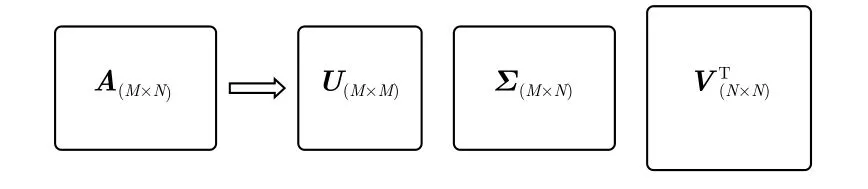
图1 奇异值分解示意图Fig.1 Singular value decomposition schematic
奇异值分解从含有噪声的数据中抽取相关特征,实现数据中噪声或冗余信息的去除。实际上,在某个奇异值(第r个)之后,其他奇异值都很小,这意味着数据集只有r个重要特征,其余特征都是噪声或者次要特征。因此,通过SVD分解,保留原始数据矩阵80%~90%的能量,可以有效去除噪声,实现数据重要特征的提取。
2.2.2 奇异值分解特征提取算法流程
奇异值特征提取如图2所示。基于奇异值分解的信号特征提取流程如下:
(1) 对输入的原始数据进行长度整理获得M×N数据矩阵
(5) 选取矩阵U中的前k列,构建M×k的矩阵

图2 奇异值特征提取示意图Fig.2 Singular value feature extraction schematic
2.3 权重归一化奇异值分解特征提取算法
在现代电子雷达中,应用比较广泛的信号调制类型主要有常规信号(NS)、调频信号(FM)及调相信号(PSK)。在使用传统时频分析等方法进行识别时,其难点主要集中在以下3个方面:
(1) 常规信号(NS)与相位调制信号(PSK)的区分;
(2) 不同相位调制信号之间的区分;
(3) 相位调制与频率调制脉冲信号之间的区分。
针对上述问题,改进奇异值分解获取信号特征的方法,提出权重归一化奇异值分解算法(WN-SVD),以提升算法的准确性。权重归一化奇异值特征提取如图3所示。

图3 权重归一化奇异值特征提取示意图Fig.3 Weighted normalized singular value feature extraction schematic
改进后的完整算法流程如下所示:
(1) 对输入的原始数据进行长度整理获得M×N数据矩阵
(5) 计算权重系数

(6) 令

其中,uij为矩阵U第i行j列的数值;
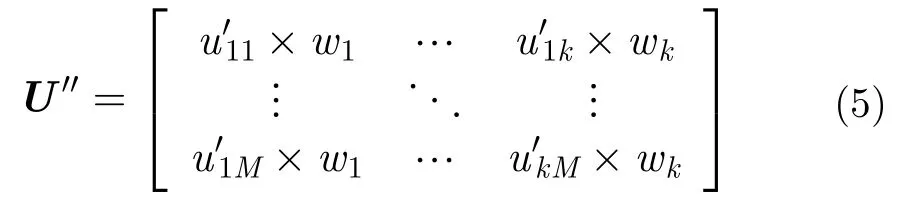
其中,第i行j列的数值;
(8) 计算
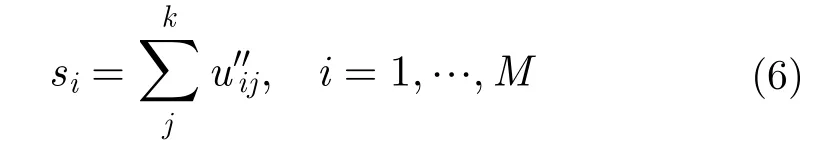

3 数据仿真
本文选取NS, LFM, BPSK和QPSK 4类信号进行算法测试。4类信号之间的差别主要体现在调制方式上,接收机接收的复信号可以建模为

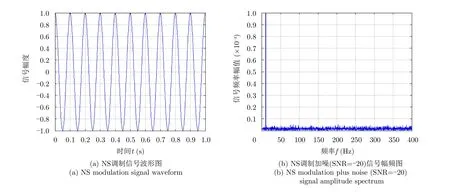
其中,A为信号的幅度参数,φ为信号的初始相位,N(t) 是方差为σ2的复加性高斯白噪声,信号的调制方式体现在f(t) 与φ (t)上。4类调制信号时域及频域如图4所示。
实验中信号的幅值A=1,信号的信噪比为-40~40 dB,间隔为5 dB。4类信号的载频fc=1000 MHz,采样频率fs=2400 MHz,脉冲宽度PW=6.3 μs,LFM调制斜率k=10 MHz/μs,带宽B=63 MHz;BPSK编码码字为[0 1 0 0 1 0 1],码元宽度为0.9 μs;QPSK信号编码码字为[0 2 0 3 1 2 0],码元宽度为0.9 μs。
利用上述方法对4类信号在不同的信噪比条件下分别进行200次仿真。随机选取4类信号每类70%的样本作为训练集,30%的样本作为测试集进行算法验证。
4 奇异值分解滤波效果分析
本文提出的权重归一化奇异值分解算法(WNSVD)过程可逆,可以还原原始的奇异值分解结果。且在进行权重归一化过程中并未对数据进行进一步的分解滤波,因此该算法滤波主要是在初始的奇异值分解过程完成。检验算法的滤波效果只需对奇异值分解重构后的信号进行分析。为检验奇异值分解算法对加噪信号的滤波效果,本文引入了距离度量和相似性度量两种定量计算方法。
距离度量(Distance)一般用于衡量个体在空间上存在的距离,距离越远说明个体间的差异越大。欧氏距离是最常见的距离度量,指在m维空间中两个点之间的距离在2维和3维空间中的欧氏距离就是两点之间的实际距离。其定义如下所示:

相似度度量(Similarity),即计算个体间的相似程度,与距离度量相反,相似度度量的值越小,说明个体间相似度越小,差异越大。余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。其定义如下所示:

由图5可知,滤波重构信号与原始信号的欧氏距离相似度随着信噪比的增加逐渐增大,且在信噪比为-5 dB时稳定在0.82左右。在信噪比-40~5 dB的条件下滤波重构信号与原始信号的相似度均好于加噪信号,说明奇异值分解对信号具有一定的滤波作用。此外,图中在信噪比大于5 dB之后滤波重构信号与原始信号的欧氏距离相似度基本稳定,且小于加噪信号,其主要是在进行奇异值分解过程中仅保留了信号90%的能量,造成了信号的部分信息丢失,从而影响了信号的幅值。
由图6可知,奇异值分解滤波重构信号与原始信号的余弦相似度随着信噪比的增加逐渐增大,且稳定在0.94以上。余弦相似度主要是度量向量方向上的差异,映射到本文的信号中,余弦相似度主要表现信号形状上的差异,余弦相似度越接近1,信号的形状越相似。

图4 4类调制信号时域及频域示意图Fig.4 Time domain and frequency domain diagrams for four types of modulated signals
综上所述,奇异值分解虽然使信号丢失部分能量,但加大了信号间形状上的相似度。其对常用雷达信号有较好的滤波效果,可以进行数据重要特征的提取。
5 数据矩阵的行数对奇异值分解结果的影响分析
奇异值分解实际上为矩阵分解方法,其分解结果受到矩阵行数的影响。本文利用奇异值分解进行数据处理与特征提取,因此在进行特征提取前需要对行数与分解结果的关系进行分析。图7和图8分别为数据矩阵行数对滤波重构信号与原始信号的欧氏距离和余弦相似度的影响示意图。其中数据矩阵行数变化范围为20~720,数据间隔为100。奇异值分解重构中奇异值保留个数m=10。图中相似度值为每次参与运算样本的平均值。
由图7可知,滤波重构信号与原始信号的欧氏距离相似度以信噪比-15 dB为界,在低信噪比条件下欧氏距离相似度随行数增大而逐渐增大,高信噪比条件下欧氏距离相似度随行数增大而逐渐减小。这主要是因为随着数据矩阵行数的增大,矩阵整体能量在奇异值上的分布逐渐分散。在信号重构过程中m值固定时,数据矩阵行数越大则重构的信号所包含的信号信息越少。高信噪比条件下信号能量占主导地位,因此欧氏距离相似度与行数成正比;而低信噪比条件下噪声能量占主导地位,因此欧氏距离相似度与行数成反比。
由图8可知,滤波重构信号与原始信号的余弦相似度以信噪比-15 dB为界,在低信噪比条件下欧氏距离相似度随行数增大而逐渐增大,高信噪比条件下余弦相似度基本不受到数据矩阵的行数的影响。
综合以上,由于余弦相似度大小反映信号形状的相似程度且其更能反映信号间的相似程度,因此我们可知在低信噪比条件下数据矩阵的行数对奇异值分解的影响较大,在处理信噪比较低的信号时需要较多的样本参与运算。
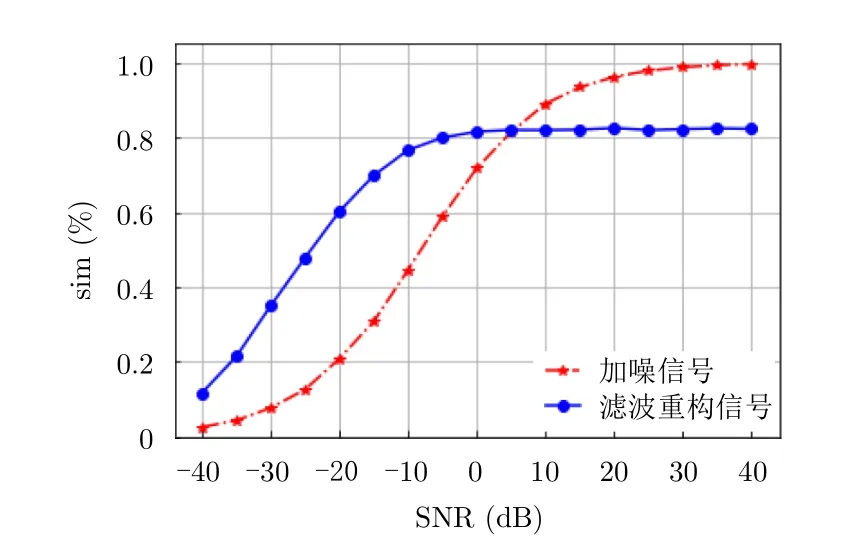
图5 奇异值分解滤波重构信号及加噪信号与原始信号的欧式距离相似度对比示意图Fig.5 Schematic diagram of the Euclidean distanceof the reconstructed signal and the noisy signal with the original signal with the signal-to-noise ratio

图6 奇异值分解滤波重构信号及加噪信号与原始信号的余弦相似度随信噪比变化示意图Fig.6 Schematic diagram of the cosine similarity of the singular value decomposition filter reconstructed signal and of the original signal with the signal-to-noise ratio
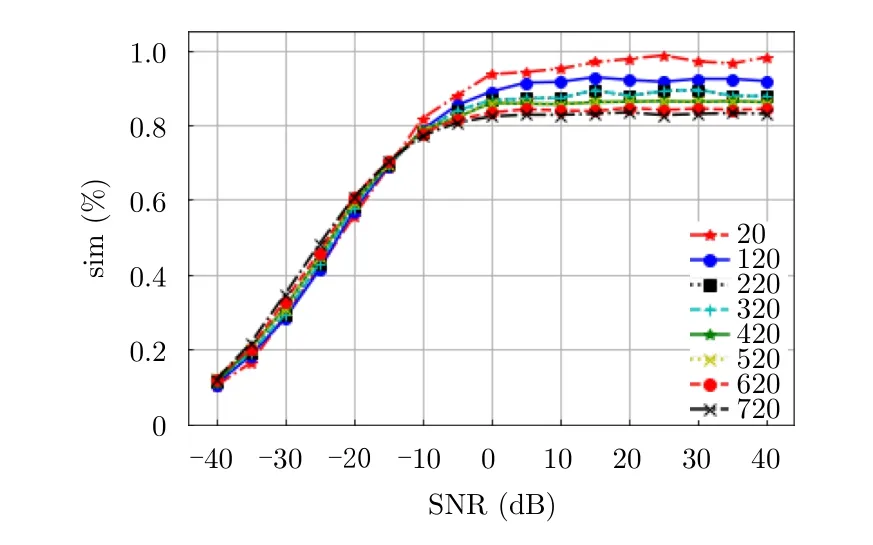
图7 数据矩阵行数对奇异值分解重构信号与原始信号欧氏距离影响示意图Fig.7 Schematic diagram of the influence of the number of rows of data matrix on the singular value decomposition reconstructed signal and the original signal Euclidean distance
6 权重归一化奇异值分解算法识别效果分析

图8 数据矩阵行数对奇异值分解重构信号与原始信号余弦相似度影响示意图Fig.8 Schematic diagram of the influence of the number of rows of data matrix on the singular value decomposition reconstructed signal and the cosine similarity of the original signal
为验证权重归一化奇异值分解算法(WN-SVD)在识别过程中的准确性,本文选取了文献[22]中的基于PCA特征提取算法进行对比实验。两种算法均选取保存原始信号能量的90%进行特征提取,且使用相同参数的分类模型进行对比分析。
文中辐射源信号识别模型的训练流程图如图9所示。其中,识别模型的输入数据为利用权重归一化奇异值分解特征提取算法所获得的特征T。模型最终输出类别为置信度最高的类别,本文识别实际上是一个多分类问题,可能存在最终输出结果置信度较低的情况。为避免上述情况,对模型最终输出结果置信度进行限制:当输出类别置信度 α满足 α>φ(φ为给定阈值)时,保留判别结果,否则舍弃。

图9 辐射源信号识别模型的训练流程图Fig.9 Radiation source identification model training flowchart
定义信号平均识别准确率为:

定义每类雷达信号的识别正确率为:

式中,Pr为平均识别准确率,Pri为第i类信号的识别准确率,Nri为第i类信号识别正确的个数,Ni为第i类雷达信号总个数。
文中选取随机森林、K近邻法、朴素贝叶斯算法及逻辑回归4种分类模型进行对比分析。测试过程中置信度α=0.65,其识别结果随信噪比变化示意图如图10所示。
由图10可知,4种分类方法中,使用权重归一化奇异值分解算法获得特征并进行分类结果均好于使用PCA算法。使用权重归一化奇异值分解算法的分类结果趋于稳定,而使用PCA算法的结果在不同分类器中的分类效果差别较大,其中PCA算法在朴素贝叶斯模型中表现最好,在随机森林算法中表现最差。PCA算法在4种分类器中在信噪比大于5 dB条件下均表现优秀,在随机森林算法中低信噪比条件下分类效果最差。
为进一步验证基于权重归一化奇异值分解算法的鲁棒性,文中采用随机森林算法对两种特征提取算法在不同置信度条件进行进一步分析。图11和图12分别为权重归一化奇异值分解特征提取算法与PCA特征提取算法在不同置信度参数下识别准确率随信噪比变化分布图。实际上置信度参数越大对特征准确度的要求越高,即对信号特征提取和分类算法的鲁棒性要求越高。本文两种算法均采用相同类型及相同超参数的分类模型,所以其识别率的变化即反映特征提取算法的鲁棒性。
由图11和图12可知,两种算法随置信度α 的增加其平均识别率均有所下降。显然,本文算法平均识别准确率随置信度参数增加而下降的程度远小于PCA算法,尤其是在信噪比大于-10 dB条件下,基于权重归一化奇异值分解算法的准确率始终保持在90%以上,而基于PCA算法的准确率随着置信度参数的增加迅速降低,当置信度参数提升到0.8以上后,其准确度下降得尤其显著,其最大识别正确率也在80%以下。
此外,在低信噪比条件下,权重归一化奇异值分解算法的信号识别准确率也远远高于PCA算法,以图中置信度参数为0.55的两条准确率随信噪比变化的曲线为例,当信噪比大于-10 dB时,两种算法的准确率结果相当,但是当信噪比继续下降,基于PCA算法的准确率迅速降低,当信噪比为-40 dB时其准确率只有20%,而基于权重归一化奇异值分解算法的准确率则很稳定,受信噪比变化的影响比较小。两种算法的对比表明,基于权重归一化奇异值分解算法对脉内信号识别具有良好的识别效果,且在低信噪比条件下仍表现优秀,具有较好的鲁棒性。
为了进一步分析基于权重归一化奇异值分解算法对不同调制信号的识别效果及鲁棒性,本文在上述实验的基础上,在置信度参数0.85条件下对4类信号进行进一步的分析。图13和图14分别为4类信号识别准确率随信噪比变化的分布图与4类信号在信噪比-40~-15 dB条件下的局部放大图。在信噪比大于-15 dB时,模型对4类信号的识别率均稳定在98%以上,而当信噪比低于-15 dB时信号的识别准确率均呈现不同程度的降低。但是4类信号即使在信噪比为-30 dB时识别准确率也维持在80%以上。由此表明,基于权重归一化奇异值分解算法可以有效解决辐射源信号识别中常规信号(NS)与相位调制信号(PSK)的区分、相位调制信号之间区分及相位调制与频率调制脉冲信号之间区分的难题。

图10 WN-SVD算法和PCA算法在不同分类模型识别结果随信噪比变化图Fig.10 The change chart of recognition results based on different classification models and SNR

图11 信号基于权重归一化奇异值分解特征提取方法在不同判别参数条件下准确率分布图Fig.11 Signals based on weighted normalized singular value decomposition feature extraction method for accuracy ratedistribution under different discriminant parameters
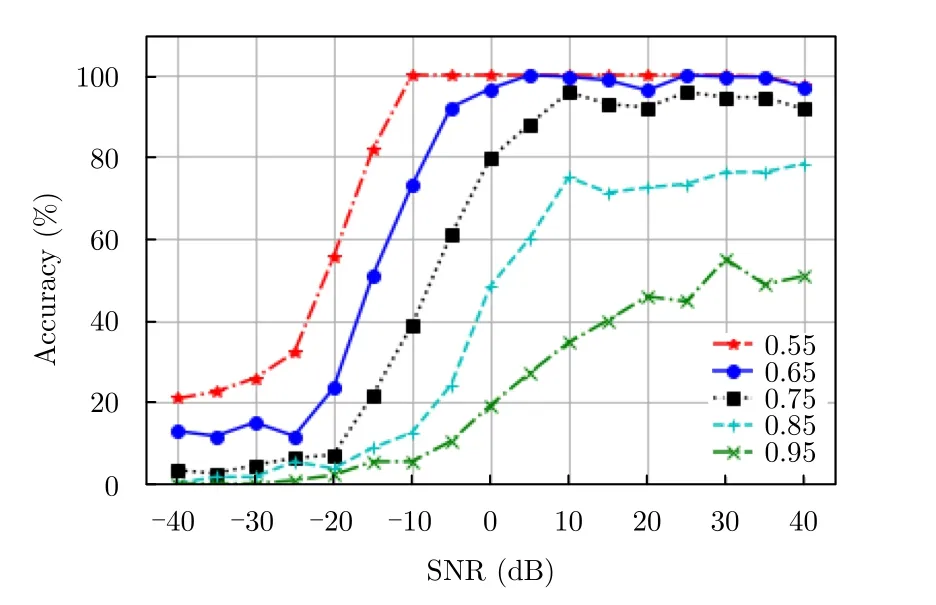
图12 信号基于PCA特征提取方法在不同判别参数条件下准确率分布图Fig.12 Signal accuracy distribution based on PCA feature extraction method under different discriminant parameters
7 总结
本文主要针对辐射源信号识别,从信号能量的角度出发,在奇异值分解基础上进行优化,提出基于权重归一化奇异值分解信号特征提取算法,用于解决辐射源信号识别中常规信号(NS)与相位调制信号(PSK)的区分、相位调制信号之间区分及相位调制与频率调制信号之间区分的难题。文中对雷达常用的4类信号进行了数据仿真,并对奇异值分解的滤波效果、数据矩阵行数对分解结果的影响及识别效果等方面进行分析。实验结果表明基于权重归一化奇异值分解信号特征提取算法分类准确率高、鲁棒性强,且受信噪比变化影响较小。
但是,本文的模型仅在高斯白噪声条件下进行了识别和分类,可能不适合其它噪声条件下的信号或某些信号失真。此外,本文的基于权重归一化奇异值分解信号特征提取算法依赖于矩阵运算,其仍存在两个难点:(1)奇异值分解对硬件存在一定的要求,如何有效地利用有限硬件资源进行高效的奇异值分解仍需进行进一步研究优化;(2)奇异值分解的输入为样本矩阵,其要求每个样本的列数相同,而在实际应用中,获取的信号样本长度是不统一的,如何处理不同维度的信号仍需更深入地研究。

图13 判别参数=0.85时4类信号在不同信噪比条件下准确率分布图Fig.13 The accuracy rate distribution chart for four types of signals with different signal-to-noise ratio when discriminating parameter =0.85

图14 判别参数=0.85时4类信号在不同信噪比(-40~-15 dB)条件下准确率分布图Fig.14 The accuracy distribution chart for four signals with different signal-to-noise ratio (-40~-15 dB) when discriminating parameter =0.85

