摇摆钢支撑框架结构抗震性能分析

蒋 聪，赵宝成

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

中心支撑钢框架结构[1]一直是多高层钢结构建筑中常用的结构形式。中心支撑钢框架结构在钢框架结构的基础上，通过在框架柱之间布置支撑来提高结构承载力及侧向刚度。支撑体系与框架体系共同作用形成双重抗侧力结构体系，不但为结构在正常受力情况下提供了一定的刚度，而且为结构在水平地震作用下提供了两道受力防线。

中心支撑钢框架结构是一种高效的抗侧力结构体系，但是在强震作用下中心支撑杆容易发生受压屈曲，导致结构刚度、承载力及耗能能力下降，主体结构破坏严重，在震后难以恢复使用功能，造成极大的经济损失。为了提高中心支撑的耗能能力，避免中心支撑杆受压失稳，受到摇摆墙结构[2]的启发，本文提出采用摇摆钢支撑代替中心支撑形成摇摆钢支撑框架结构。摇摆钢支撑框架结构由两部分组成，第一部分是作为主体承重结构的框架，第二部分是摇摆支撑钢架，摇摆钢支撑与基础铰接，摇摆钢支撑与框架之间采用耗能段连接。钢支撑的抗侧刚度大，可协调框架结构每一层的变形，使框架结构各层的位移变得更加均匀，有效地避免了框架结构出现薄弱层的问题。在强震作用下，摇摆支撑钢架与主体框架之间的耗能段首先进入塑性耗能，增加了结构的耗能能力，避免主体结构发生破坏，使得结构在震后只需替换耗能段即可恢复使用。

本文采用ABAQUS有限元软件对摇摆钢支撑结构与中心支撑结构的抗震性能进行了对比分析。从破坏模式、滞回性能、承载力、刚度退化等方面分析了支撑与框架之间不同刚度比及非耗能段采用不同钢材等级时对摇摆钢支撑结构抗震性能的影响。采用等能量原理将摇摆钢支撑结构正向骨架曲线转化为三折线模型，以此确定结构耗能段替换的层间侧移角范围，并分析刚度比与钢材强度等级对结构耗能段替换的层间侧移角范围的影响。

1 结构试件设计

模型以某3跨6榀6层钢框架为原型结构，参考相关规范，采用sap2000软件进行设计。结构层高为3.6 m，总跨度为18.6 m，其中耗能段长度为0.9 m，摇摆支撑跨度为3.6 m。框架耗能梁段、支撑、梁、柱均采用焊接H形截面钢。除了耗能梁段采用Q235B级钢材外，其余的构件全部采用Q345B级钢材。摇摆钢支撑或中心支撑结构平面布置如图1所示，布置在2、5轴及A、D轴的中间跨。

取摇摆支撑结构横向2轴一榀作为有限元分析的G1试件，如图2所示。框架边柱截面尺寸第1-3层为H550×550×16×32、第 4-6 层为 H550×550×14×28；中柱截面尺寸第 1-3 层为 H500×500×14×28、第 4-6 层为H550×550×12×24；框架梁截面尺寸为 H400×200×12×22；支撑截面尺寸为 H175×175×10×12；耗能段类型为剪切型，其截面尺寸为H400×200×12×16，加劲肋厚度为12 mm，间距为200 mm，耗能梁长度e满足式（1）。

式中，Mp、Vp是耗能梁的塑性抗弯承载力和抗剪承载力；Mp=Wpfy，Vp=0.58h0twfy，Wp为耗能梁的塑性抵抗矩，fy为耗能梁的材料屈服强度，h0为耗能梁腹板高度，tw为腹板厚度。

同样取中心支撑结构横向2轴一榀作为对比试件（试件ZXZC）。如图3所示，其梁柱、支撑截面尺寸均与试件G1相同。

图1 平面布置图

图2 摇摆钢支撑结构

图3 中心支撑结构

为了分析摇摆支撑与框架层间刚度比对摇摆钢支撑结构抗震性能的影响，设计了一组改变G1试件刚度比的G系列试件。本文刚度比指摇摆钢支撑的层间刚度与两边框架层间刚度之比。根据曲哲、叶列平[3-4]及Gregory A.MacRae[5]的研究，刚度比r计算公式见式（2），支撑和框架的层间刚度计算公式见式（3）和式（4）。

其中，k为摇摆钢支撑的层间剪切刚度，K为两边框架的层间刚度；h为结构层高，E、I为柱和支撑的弹性模量与惯性矩，A为支撑截面尺寸；n为每层框架柱的数量，L为摇摆钢架中支撑的长度，l为摇摆钢架的跨度。

通过改变支撑截面尺寸改变支撑与框架的层间刚度比，根据公式（1）-（3），对G系列试件支撑截面尺寸进行设计和选择，具体截面尺寸见表1所列。

表1 G系列试件支撑截面尺寸表

为了研究钢材强度等级对摇摆钢支撑结构抗震性能的影响，设计了一组Q系列试件，共包含6个试件：G5及Q-1、Q-2、Q-3、Q-4、Q-5。Q系列试件是在G5试件的基础上，仅改变非耗能构件的钢材强度等级形成的。 Q-1至Q-5的钢材等级分别对应Q235B、Q390B、Q420B、Q460C、Q550C。

图4 简化应力-应变关系

2 有限元模型验证

2.1 钢材本构关系

有限元分析时，所用钢材本构模型采用如图4所示的三折线模型，施加荷载时考虑包辛格效应及几何非线性，采用随动强化模型。采用Mises屈服准则定义材料的塑性特征，钢材的弹性模量为2.06×105N/mm2，泊松比取0.3。

2.2 单元划分及边界条件

由于模型的层数较多，采用实体单元会导致计算量过大，所以采用壳单元进行建模（S4R单元4节点减缩积分），能够大大减小计算量且与实体单元的精度相似。在结构的连接节点中，焊接截面全部采用绑定接触。框架柱脚通过耦合约束其所有自由度来模拟与基础的固接，约束梁的侧向自由度以防止结构面外失稳。

2.3 加载方案

ABAQUS有限元分析时采用倒三角分布模式进行位移加载[6]，在各层柱加载点处施加水平侧向位移。1层至 6 层对应的荷载比例为 1∶2∶3∶4∶5∶6。 循环往复荷载由位移控制， 按照 Δy/4、Δy/2、Δy/4、Δy、1.5Δy、2Δy、2.5Δy、3Δy……的方式进行，其中Δy结构的屈服位移，由ABAQUS有限元软件对模型进行单向推覆分析确定。结构屈服前每级位移循环一次，屈服后每级位移循环两次，直至试件破坏。

2.4 有限元模型验证

为了保证有限元模拟的准确性，本文选取文献[7]中的Y形偏心支撑钢框架试验进行有限元模型验证，按前文所述方法建立有限元模型。相关参数均按照文献[7]中试验的参数选取，加载方式亦如前文所述。

图5-6给出了试验及模拟的滞回曲线和骨架曲线。由此可知，有限元模拟的滞回曲线呈较为饱满的梭形，与试验的滞回曲线基本一致。有限元模拟得出的骨架曲线与试验骨架曲线基本重合，只有极限荷载与极限位移略大。综上可知，本文所采用的有限元分析方法可以用于摇摆钢支撑结构抗震性能研究。

图5 滞回曲线对比

图6 骨架曲线对比

3 摇摆钢支撑结构与中心支撑结构抗震性能对比

3.1 试件ZXZC破坏模式

试件加载过程中，当试件顶层位移达到32.6 mm时，底层与第2层支撑首先进入塑性，其他构件保持弹性状态；随后当试件顶层位移达到56.1 mm时，底层与第2层支撑塑性发展更大，第2层支撑发生屈曲，第3层支撑也开始进入塑性，其余构件仍然保持弹性；当试件顶层位移达到140.4 mm时，第2层和第3层梁柱节点腹板、中柱柱脚进入塑性；当试件顶层位移达到368.8 mm时，中柱柱脚处腹板大面积达到极限应力，试件破坏。试件破坏时的应力云图如图7-8所示，可见试件破坏主要发生在中心支撑跨底部两层，支撑发生屈曲，底层中柱柱脚处应力过大，破坏严重。

图7 ZXZC试件应力云图

图8 ZXZC试件第1层与第2层支撑跨应力云图

3.2 试件G1破坏模式

当试件顶层位移达到45.1 mm时，首先进入塑性是试件的1层耗能段腹板，此时，试件其余部分仍然维持在弹性阶段；随后试件顶层位移达到87.2 mm时，试件的第2-4层耗能段腹板先后进入塑性，其余构件仍然维持弹性；当试件顶层位移达到237.2 mm时，底层中柱柱脚及耗能段与柱的节点处进入塑性；当试件顶层位移达到325.0 mm时，第4至6层耗能段腹板进入塑性；当试件顶层位移达到405.1 mm时，1、2层耗能段腹板全部达到极限应力，结构视为破坏。试件破坏时的应力云图如图9-10所示。可以发现，试件的塑性变形主要集中在耗能梁段与梁柱节点处，而耗能梁段塑性发展最为严重，大部分主体构件均能够保持弹性。G1损坏主要集中在耗能梁段，而ZXZC主体部件损坏严重，G1的破坏模式比ZXZC更为理想。

图9 G1试件应力云图

图10 G1试件1～3层耗能段应力云图

3.3 滞回曲线

ZXZC与G1的滞回曲线如图11所示。其中荷载为施加于结构的水平荷载之和，位移为顶层水平位移。在加载初期，两个试件均处于完全弹性阶段，力-位移曲线均呈一条直线；当继续加载至ZXZC的支撑屈曲、G1耗能段屈服后，两试件的滞回曲线斜率开始下降，说明其刚度开始下降；ZXZC的滞回曲线有一定的捏缩，主要是因为中心支撑产生了屈曲。G1的滞回曲线比较饱满，说明其耗能能力良好。

3.4 骨架曲线

ZXZC与G1的骨架曲线如图12所示。在初始阶段，两试件都处在弹性阶段，曲线基本重合，说明两个试件初始刚度比较接近；加载后期，ZXZC的骨架曲线高度要高于G1的骨架曲线，说明ZXZC的极限承载力比试件G1大；然而G1的骨架曲线极限位移大于ZXZC，说明G1具有更好的变形能力。

3.5 刚度退化曲线

ZXZC与G1的刚度退化曲线如图13所示。初期ZXZC的初始刚度与G1的初始刚度基本相同。随着位移的增大，ZXZC的刚度退化曲线下降速度大于G1的下降速度。加载后期两个试件的刚度退化速度趋于平缓，此时ZXZC与G1的剩余刚度相差不大。

图11 滞回曲线对比

图12 骨架曲线曲线对比

图13 刚度退化曲线对比

4 刚度比对结构抗震性能的影响

4.1 滞回曲线

模型G1-G5的结构基底剪力与顶点位移的滞回曲线如图14（a）-（e）所示。其中荷载为施加于结构的水平荷载之和，位移为顶层水平位移。整体来看，结构滞回曲线均呈梭型，较为饱满，表现出良好的耗能能力，说明其抗震性能良好。5个试件的滞回环包围面积大致相同，说明其耗能能力相似，刚度比的改变对摇摆钢支撑结构的耗能能力影响比较小。

4.2 骨架曲线

图14 G系列试件滞回及骨架曲线

G1～G5的骨架曲线如图14（f）所示。加载初期5个模型均处于弹性状态，骨架曲线基本保持一致，说明其刚度比较接近。随着荷载的增加，5个试件的骨架曲线基本在相同的位移点开始出现转折，斜率下降，说明5个试件进入塑性的时间比较接近。各试件进入塑性以后，骨架曲线开始出现差别，支撑与框架层间刚度比大的试件骨架曲线比刚度小的试件略高，说明随着刚度比的增加，结构的承载能力逐渐提升。

4.3 变形模式

模型G1～G5的整体位移曲线如图15所示。可以看出，刚度比较小时，结构整体位移曲线呈现为半U形，但是随着刚度比的增加，结构的位移曲线越来越接近一条直线，说明刚度比的增加对结构的变形模式有较大改善。

层间位移角是抗震性能中一项很重要的指标，通过对图16的分析可知，从模型G1到G5，随着刚度比的增大，各层的变形逐渐趋于一致，顶部的层间位移角与底部的层间位移角更加接近，G5试件的层间位移角曲线几乎为一条直线。这是因为摇摆支撑的刚度较小时对两边框架变形的控制能力不强，仍然存在框架结构的变形模式，各层层间位移角相差很大，顶部结构变形小，不能充分发挥其抗震性能，而底部变形过大，容易出现薄弱层；随着摇摆支撑刚度的增大，协调了框架的变形，使得各层层间位移角分布更加均匀，结构上部变形相对框架结构增大，充分发挥了上部结构的耗能性能；底部变形减小，结构整体变形模式更加合理。

4.4 刚度退化曲线

G系列试件的刚度退化规律如图17所示。从图17可以看出，刚度比变化对结构的刚度退化速度及剩余刚度影响不大。放松了摇摆支撑跨与基础连接后，摇摆支撑跨刚度的改变对结构整体刚度的影响较小。

图15 整体位移曲线对比

图16 层间位移角曲线对比

图17 G系列试件刚度退化曲线

4.5 承载力和延性

G系列各试件的特征荷载、位移及延性系数如表2所列。由表2可知，随着刚度比的提高，结构极限荷载随之增大。所有结构的延性系数均在6.49～6.94之间，具有较好的延性。由此可知，刚度比的提高可以增大结构的极限承载力，但是延性变化不大。

表2 试件特征荷载、位移及延性系数

4.6 耗能段可替换层间侧移角范围

摇摆钢支撑钢框架结构属于损伤控制结构[8]的一种，其屈服顺序具有明显的多阶段特性，如图18所示。阶段一：弹性阶段，结构构件均保持弹性；阶段二：快速修复阶段，耗能段进入塑性耗散地震能量，其余构件仍保持弹性；阶段三：防倒塌阶段，此时受力较大的主体构件也开始进入塑性。其中，阶段二，即快速修复阶段为替换耗能梁段的合理范围。

为了快速确定摇摆钢支撑钢框架结构耗能段可替换范围，利用等能量法[9]将G系列试件的正向骨架曲线简化三折线模型，用以确定G系列试件耗能段替换的层间侧移角的上限与下限。其结果列于表3中。

分析表3数据可知：G系列试件底层耗能段替换层间侧移角范围的上限都在0.004 0左右，下限都在0.016 5左右，其间侧移角范围基本相同。顶层耗能段替换层间侧移角范围下限在0.003 0左右，基本相同，但是其上限随着刚度比的增加而有所增大。其主要原因是随着刚度比的增加，摇摆钢支撑对两边框架变形的协调能力增强，使得结构顶层的侧向水平位移增大，顶层耗能段变形增大，耗能能力发展更充分。

图18 摇摆钢支撑结构塑性发展阶段

表3 G系列试件替换范围比较

5 钢材强度等级对结构抗震性能的影响

5.1 滞回曲线

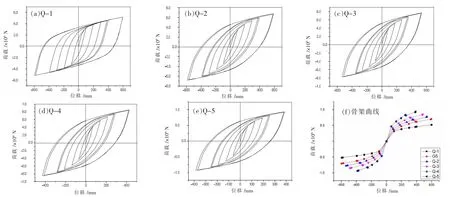
图19 Q系列试件滞回及骨架曲线

Q系列试件的滞回曲线如图19（a）-(e)所示。其中荷载为施加于结构的水平荷载之和，位移为顶层水平位移。可以看出：G5及Q-1至Q-5的滞回曲线均呈梭形，随着钢材强度等级的增大，结构的极限承载力也依次增加；随着钢材强度等级的增大，滞回曲线包围的面积并没有明显地减小，说明对结构耗能能力影响不大。

5.2 骨架曲线

Q系列试件的骨架曲线如图19（f）所示。可以看出：在弹性阶段，随着钢材等级的提高，试件的骨架曲线斜率略有增大，说明钢材等级的提高可以提高结构刚度。在进入弹塑性阶段后，试件骨架曲线差别明显，钢材强度等级提高，试件的骨架曲线高度相应地增加。说明钢材等级的提高可以有效提升结构的极限承载力。

5.3 刚度退化曲线

Q系列试件的刚度退化曲线如图20所示。结构的刚度退化速度随着结构钢材强度等级的增大逐渐减小，而结构的剩余刚度随着钢材强度等级的增大而增大。因此，钢材强度等级的提升可以减小结构的刚度退化速度，减轻破坏程度。

5.4 承载力和延性

Q系列各试件的特征荷载值、位移以及延性系数如表4所列。由表4可知，随着钢材强度等级的提高，结构极限荷载随之增大。结构的延性系数均在5.23以上，表明其都具有较好的延性性能。但是随着钢材强度等级的提高，结构的屈服位移有所增大，导致延性降低。因此，提高钢材强度等级可以增大结构的极限承载力，但是延性会有所降低。

图20 Q系列试件刚度退化曲线

表4 试件特征荷载、位移及延性系数

5.5 耗能段可替换层间侧移角范围

按照4.6节所述方法，将Q系列试件的正向骨架曲线简化三折线模型，用以确定Q系列试件耗能段替换的层间侧移角范围。其结果列于表5中。

表5 Q系列试件替换范围比较

Q系列试件具有基本相同的耗能段替换层间侧移角范围下限，均在0.004 1左右。这是因为不同钢材等级的Q系列试件在处于弹性阶段时，其弹性模量均相同，而结构的尺寸没有变化，耗能梁段也完全相同，所以Q系列试件的耗能段基本会在同时进入塑性阶段。

Q试件耗能段替换层间侧移角范围的上限随着钢材强度等级的提高而有所增大，从0.012 9增至0.017 0。这是因为钢材强度等级提升后，主体结构进入塑性的时间向后延迟，使得其进入塑性时具有更大的层间侧移角。所以Q试件的耗能段替换的层间侧移角范围的上限随之提升，层间侧移角范围也随之变大。与G5试件相比，Q-1的耗能段替换的层间侧移角范围降低了7%，Q-2至Q-5的却提高了3%、7%、11%、25%。

6 结论

（1）摇摆钢支撑结构与普通中心支撑结构相比破坏模式合理、耗能能力强。摇摆钢支撑结构主要由耗能段进入塑性耗能，主体结构损伤较小，震后替换耗能段即可恢复使用功能。（2）摇摆钢支撑结构能够有效地减小结构层间位移角，改变结构的变形模式，防止薄弱层的出现。随着刚度比的增加，摇摆钢支撑结构的整体位移逐渐趋向于一条直线，层间位移角趋于均匀，变形模式更合理。（3）结构钢材强度等级越高，结构的极限承载力、剩余刚度都有增加，但是延性会有所降低。提高结构钢材强度等级可以减轻结构的破坏程度，降低震后修复难度。（4）使用三折线简化模型能够准确地确定摇摆钢支撑结构耗能段替换的层间侧移角范围；增大结构刚度比能够增加结构顶层耗能段的层间侧移角替换范围的上限；提高结构非耗能构件钢材强度等级后，结构各层耗能段层间侧移角替换范围的下限保持不变，上限逐渐提高。