化学爆炸等效单自由度结构体系抗力动力系数分析
耿少波, 葛培杰, 刘亚玲, 李 洪
(1.中北大学 土木工程学科部,太原 030051;2. 长安大学 桥梁结构安全技术国家工程实验室,西安 710064;3.大连理工大学 水利工程学院,大连 116024)
重要建筑物及防护结构一般需进行抗爆设计,爆炸荷载作为一种偶然作用,通常由核爆和化学爆炸两种类型组成。核爆概率低,其冲击波正超压作用时间长,常大于建筑结构塑性最大变形时间;化学爆炸概率较高,冲击波正超压衰减快、爆炸作用影响区域较小,正超压作用结束后结构再完成最大塑性变形。本文以化学爆炸产生的正超压冲击波为考虑荷载类型,允许建筑结构在爆炸荷载作用下进入弹塑性状态,研究不同延性比条件下爆炸荷载等效静载动力系数的变化特点。
由于理论分析较为复杂、组织结构抗爆试验难度大,大部分学者采用商业软件分析各种类型结构在爆炸作用下的受力及破坏特征。设计人员最熟悉的荷载类型为静载,如果能将化学爆炸荷载简化处理为静载类型,可明显提高结构抗爆设计效率[1-2]。因此,《人民防空地下室设计规范》、《平战结合人民防空工程设计规范》等规范均推荐采用基于抗力动力系数的等效静载完成抗爆设计。
关于爆炸荷载等效静载的计算问题,国内外学者开展了一些研究。方秦等[3]分析了爆炸作用下承重柱的等效质量、等效荷载,推导了弹性阶段响应解析解;穆朝民等[4]采用等效静载方法研究了室内爆炸流的动载系数,并用有限元方法进行了验证;任秀敏等[5]采用等效静载法求解了天线罩的最大位移,荷载类型为线性荷载;杨科之等[6-7]深入研究了延性比及结构参数对动力系数的影响规律,未对荷载正超压作用时间与直线等效荷载等效作用时间进行转换研究;边文凤等[8]采用Cole提出的爆炸等效静载方法对水下船体遭受爆炸冲击波作用时进行了计算,指出了船体的破坏模式,未对等效荷载函数模式及作用时间做进一步分析;伍俊等[9]以一实例完成了防爆墙的等效静载设计与有限元对比;颜海春等[10]对封堵梁进行了化爆作用等效荷载内力及抗力计算;杨涛春等[11]和Chen等[12]分别对混组合梁及地下拱结构进行爆炸作用计算,并验证了等效单自由体系方法简便性;陈俊杰等[13]指出了阻尼系统对结构等效静载抗爆设计的提高作用。动力系数计算与荷载时长、弹塑性阶段位移响应有关,且按等冲量等效出的线性衰减荷载作用时长短于真实的爆炸荷载作用时长,两种荷载模式的动力系数有何区别,目前鲜有研究。
爆炸冲击波荷载衰减函数可用多项式为基底的级数拟合[14-15],为此,本文首先确定线性等效荷载与多项式曲线拟合衰减荷载时长关系,推导两种荷载模式等效单自由度体系弹塑性阶段动力系数公式,进而确定两种荷载模式计算精度。
1 弹塑性体系动力微分方程
1.1 等效单自由度微分方程
由结构动力学等效单自由度弹塑性理论可知,结构等效静载荷取决于冲击波荷载超压函数、超压作用时间和结构自振频率。化学爆炸荷载正超压作用时长及等效时长很小,在此时间区间内结构来不及完成最大位移响应[16]。根据达朗贝尔原理,弹性阶段爆炸荷载等效动力体系微分方程
(1)
式中:kM-L为弹性阶段等效质量-荷载比值;m为每延米质量;l为长度;W(t)为动位移;K为等效刚度系数;Δp(t)为爆炸荷载正超压函数。
结构在tT时刻进入塑性阶段,此后结构动力微分方程为
(2)
式中:km-l为塑性阶段等效质量-荷载比值;qm为塑性阶段构件最大抗力。
等冲量线性衰减荷载的函数表达式为
(3)
多项式拟合曲线衰减荷载函数表达式为

(4)
式中:Δpm为正超压峰值;f(t)为归一化时程函数;ti为等效作用时长;t+为真实作用时长。如图1所示。
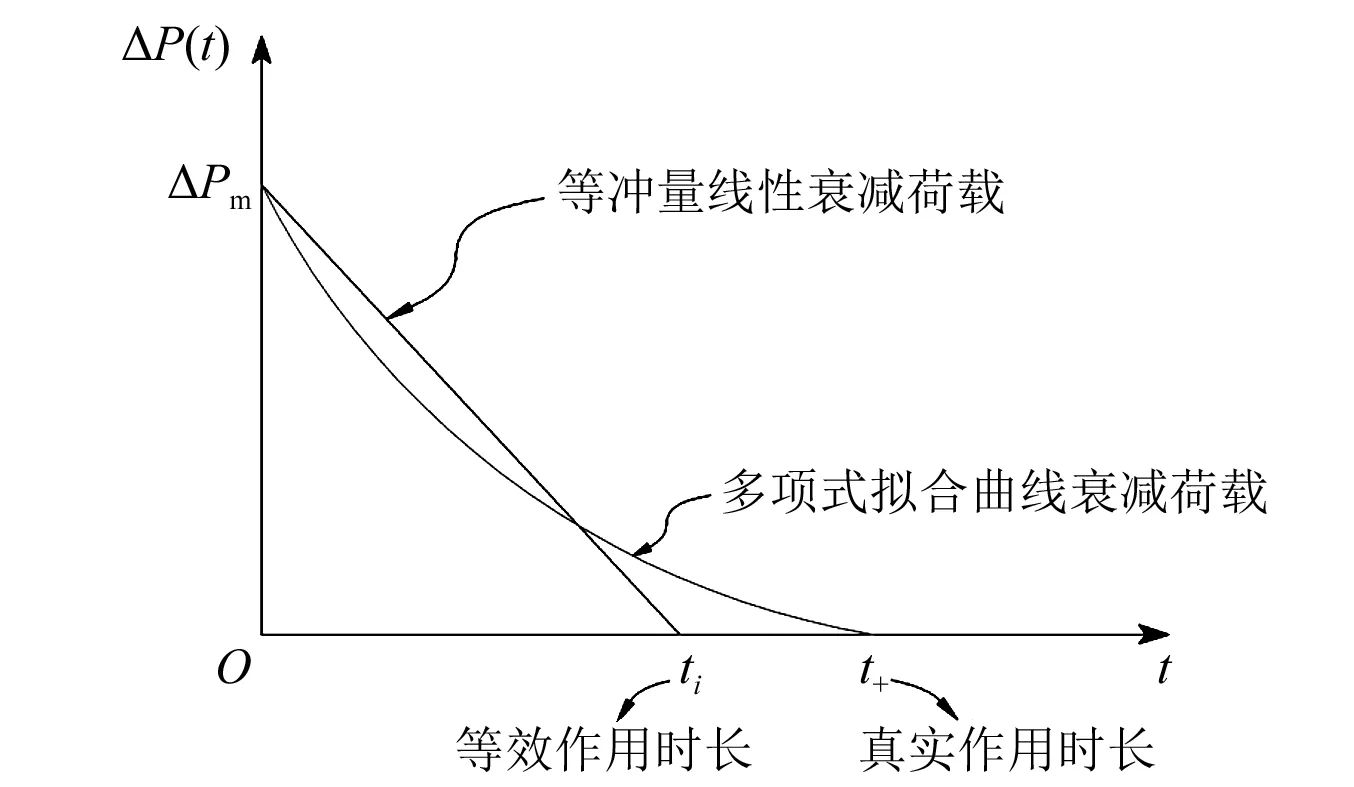
图1 化爆荷载类型对比图Fig.1 Chemical explosion comparison diagram
根据Duhamel积分原理,由式(1)可得
(5)
(6)
弹性响应结束即将进入塑性时位移及速度为
(7)
(8)
由式(2)、式(7)、式(8)可得结构振动塑性位移及速度为
(9)
W(t)=wT+vT(t-tT)+
(10)
结构弹塑性阶段等效静载抗力动力系数为
(11)
1.2 等效时长与作用时长关系
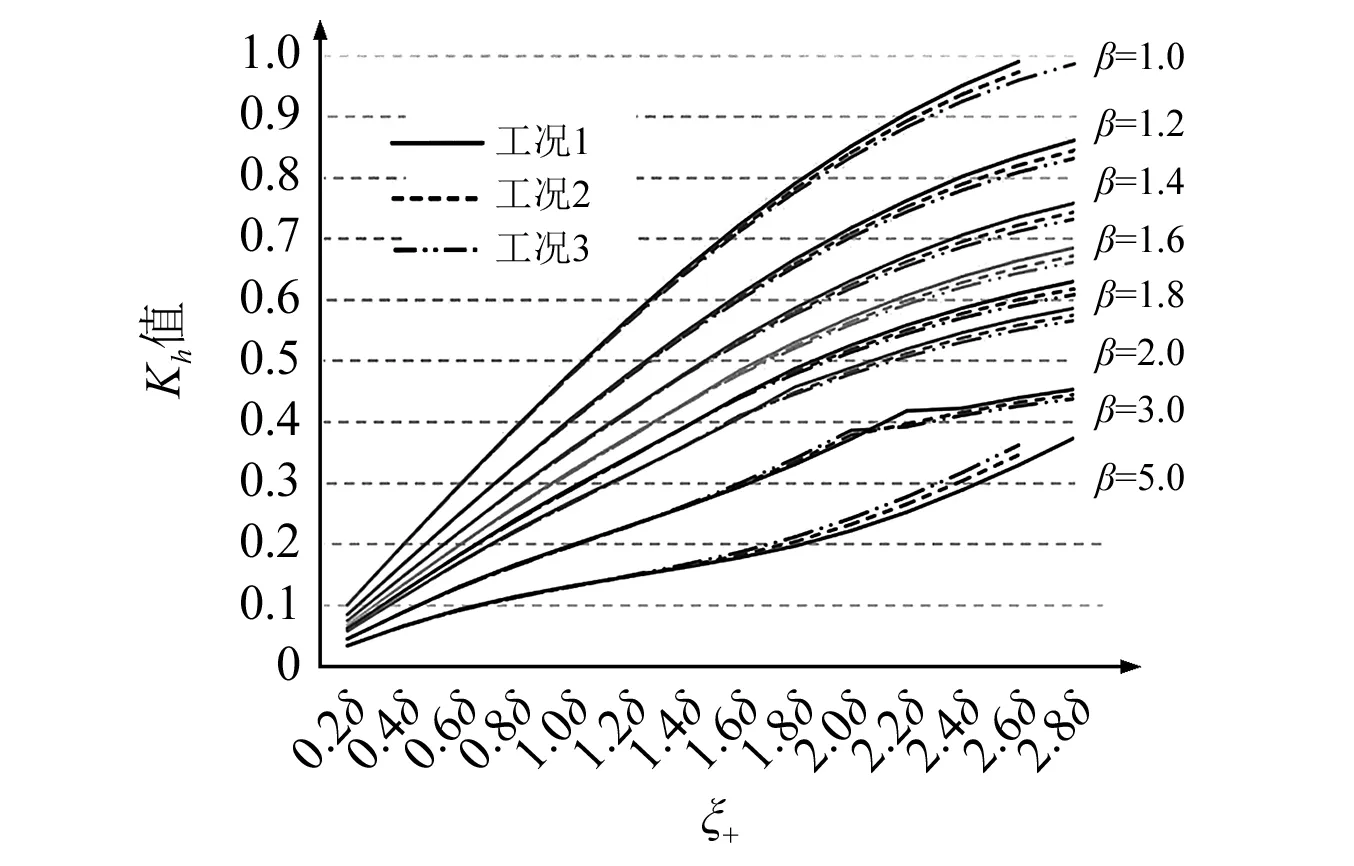
由真实作用时长t+、超压峰值Δpm及形状调整参数a,且化学爆炸可取1.27 (12) 则线性等效荷载的等效时间为 (13) 对于多项式拟合曲线衰减荷载,不存在等效时长,据a的范围确定其曲线的调整幅度,有冲量定义及式(4)、式(12)可知 (14) 由a的不同取值,可确定t+及相应的b0,b1取值,为便于后续分析,典型数值取值见表1。 表1 等效时长及相关参数表 结构在爆炸荷载作用下进入塑性阶段完成设计要求的延性比,受结构自身特性与爆炸荷载时长限制,分为两种类型:①承受爆炸荷载的建筑结构刚度较低,由于正超压作用时间较短,爆炸冲击波正超压结束时,结构尚未完成弹性变形,在后续结构自由振动期间逐步完成结构塑性变形,达到设计所需的延性比,对应的时间关系为ti 令ξT=ωtT,ξi=ωti,ξ+=ωt+,由式(7)可知线性等效荷载动力系数为 (15) 多项式曲线拟合衰减荷载的动力系数为 (16) 若定义 则由式(15)可得 (17) 定义 用A*,B*替换式(17)中A,B,即为得多项式曲线拟合衰减荷载cosξT公式,且 (18) 由式(8)可得弹性阶段结束时,线性等效荷载下速度及比值 vT=Wcm[cosξT-cos(ξT-ξi)+ξisinξT]/ti (19) (20) 同理,可得多项式曲线拟合衰减荷载下比值 (21) 由式(9)及v(tm)为0可推导 (22) 由式(10)及v(tm)为0可推导得出 (23) 将式(22)代入式(23),即 (24) 由于 (25) 将式(22)、式(23)、式(20)代入式(24)可得线性等效荷载的延性比表达式(26),同理可得多项式曲线拟合衰减荷载的延性比表达式延性比式(27) (26) (27) 上述表达式为同一结构基于不同延性比β、结构荷载参数ωti(ωt+)的关于线性等效荷载与多项式曲线拟合衰减荷载的动力系数。 令ξm=ωtm,可知ξT<ξi<ξm或ξT<ξ+<ξm,线性等效荷载的动力系数可推导出 (28) 多项式曲线拟合衰减荷载的动力系数为 (29) 由式(8)线性等效荷载函数即将进入塑性阶段的速度及比值 vT=Wcm(-1+cosξT+ξisinξT)/ti (30) (31) 多项式曲线拟合衰减荷载函数相应数值 (32) 由式(9)及v(tm)为0可知线性等效荷载 (33) 多项式曲线拟合衰减荷载积分后其数值为 (34) 由式(31)、式(33)线性等效荷载参数 (35) 由式(32)、式(34)多项式曲线拟合衰减荷载参数 (36) 由式(10)分别可得线性等效荷载的延性比式(37)及多项式曲线拟合衰减荷载函数的延性比式(38) (37) (38) Kh为隐式表达式,求解时可先确定延性比,再根据不同的时间参数求出。 按表1所示三种工况参数分别进行计算动力系数计算,ωti范围为0.2~2.8,结构设延性比范围为1~5。令δ=t+/ti,工况1的详细结果汇总为表2,所有工况结果如图2和图3所示。 表2中采用灰度区分的为多项式曲线拟合衰减荷载模式计算结果,其中弹性设计状态的底纹采用灰度5%的浅灰,较晚进入塑性状态的底纹采用灰度15%的中灰,较早进入塑性状态的底纹采用灰度25%的深灰。 为便于对比,线性等效荷载模式计算结果以相对误差,标注在按多项式曲线拟合衰减荷载模式计算结果括号内侧,未标注代表无解。 结合表2、图2、图3可知,两种荷载模式均在各自两种塑性阶段分界线处都能光滑过渡,线性等效荷载模式ωti计算范围2.2小于多项式曲线拟合衰减荷载模式ωt+计算范围2.8δ。 按多项式曲线拟合衰减荷载计算时,当ωt+<1.4δ时,对同一β与ti,ω越大,结构越较早进入塑性阶段,且Kh越大,此时若β较大,且ωti较大时,均为较早进入塑性阶段;各工况计算结果说明在同一β及ωt+,存在按多项式曲线拟合衰减荷载模式为较早进入塑性阶段,而按线性等效荷载为较晚进入塑性阶段情况。 按多项式曲线拟合衰减荷载计算时,当ωt+>1.4δ时,为较晚进入塑性阶段,而按线性等效荷载计算动力系数时,为荷载较早进入塑性阶段。ωti为较大数值时,β降低的过程依次对应较早进入塑性到较晚进入塑性、再到纯弹性状态(β=1)。采用线性等效荷载模式从较早进入塑性阶段跳跃到弹性状态,这种差别在于等冲量表示爆炸荷载传递给结构能量相同,但线性衰减荷载模式下等效时长变小,且减小幅度很高,对于刚度较大结构,吸收能量时间变短, 在时间上缓慢进入塑性状态的过程缩减,误认为较早便进入塑性状态。 表2 工况1抗力动力系数Kh 图2 直线型衰减荷载动力系数Fig.2 Dynamical coefficients for linear attenuation load 图3 多项式拟合衰减荷载动力系数Fig.3 Dynamical coefficients for polynomial attenuation load 由计算可知:当β<1.6时,工况一a为1.27,抗力动力系数按线性等效荷载计算的数值都高于按多项式曲线拟合衰减荷载计算数值,平均高1.8%,最大为10%;工况二对应a为1.44时具备同样特征,平均高2.5%,最大为11.2%;工况三对应a为1.61具备同样特征,平均高3.3%,最大为12.3%,说明由线性等效荷载计算时数值偏保守,且衰减曲线越陡,差值越明显。 当β>1.6且ωti较大时,Kh按线性等效荷载计算小于按多项式曲线拟合衰减荷载计算结果,各工况最大幅度为19.1%,16.4%及18.0%,此时采用线性等效荷载偏不安全;β取5.0时会有线性等效荷载计算无解而多项式曲线拟合衰减荷载有解情况。 以化学爆炸为爆炸荷载类型,推导出线性等效荷载与多项式曲线拟合衰减荷载等效静载抗力动力系数表达式,结合算例得到以下认识: (1)两种计算结果中较晚与较早进入弹塑性阶段动力系数分界处均平滑过渡,在共同计算范围内差异较小。 (2)对同一ωt+数值,随着β增大,Kh降低,多项式曲线拟合衰减荷载划分塑性结果空间为三部分,可完整显示出从弹性、较晚进入塑性至较早进入塑性状态转换,线性等效荷载划分塑性结果空间为两部分,因此弹塑性变化在部分空间不连续。 (3)β较小时,多项式曲线拟合衰减荷载的可求解区间不仅大于线性等效荷载函数,且在两种荷载重叠区间内Kh偏小。 (4)β较大时,线性等效荷载Kh可求解区间更小,且在两种荷载重叠区间内Kh偏小,采用此抗力系数设计结构可能偏不安全。
2 弹塑性阶段动力系数推导
2.1 较晚进入塑性阶段
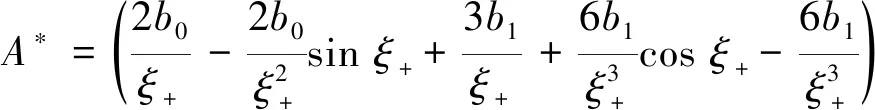
2.2 较早进入塑性阶段

3 抗力动力系数计算算例
3.1 各工况动力系数计算
3.2 结果定性分析


3.3 结果定量分析
4 结 论

