基于应变模态参数的结构瞬态载荷识别方法研究

周 玙， 刘 莉， 周思达， 王大宇， 邵玉佩

(北京理工大学 宇航学院 飞行器动力学与控制教育部重点实验室，北京 100081)

飞行器结构在飞行或运输过程中经常会受到瞬态载荷的作用。对实际工作过程中所受载荷进行识别，将为飞行器结构的优化、故障评估、寿命预测提供基础。然而，在实际工程中，往往载荷无法通过传感器直接测得，如：测点不可达、载荷作用点较多，以及涉及流固耦合时。而一般情况下，结构的动响应是较为容易得到的。因此，通过载荷识别方法确定载荷具有较高的实用价值。

载荷识别属于结构动力学的第二类反问题。在识别瞬态载荷时时域法具有较大优势，国内外许多专家学者对此做过许多研究：周晚林[1]通过有限元逆分析和人工神经网路相结合的综合方法对智能结构的冲击载荷进行识别；蔡元奇[2]通过假设载荷形式为二次函数利用Duhamel积分式推导出了时域非递推载荷识别模型；严刚等[3]应用遗传算法对复合材料冲击载荷的识别进行了研究。刘杰[4]通过求解核函数矩阵对载荷进行识别并研究了其正则化方法；毛伯永等[5]提出了基于瞬态统计能量分析理论的冲击载荷识别方法，识别除了载荷作用位置和输入能量；张磊等[6]在总体最小二乘法基础 进行Tikhonov正则化后利用共轭梯度法求最优解对载荷进行识别；张方等[7]利用广义正交多项式作为形函数推导了基于时间有限元的动载荷识别模型，该方法尤其适用于瞬态载荷的识别。Xu等[8]提出一种根据不完全测量信息的自适应迭代最小二乘法对载荷和参数进行识别。朱斯岩等[9]通过频域修正时域载荷识别结果，并应用于实际工程。

目前，载荷识别主要基于位移响应和加速度响应。然而，对于运行中的飞行器而言，由于传感器安装、排线等约束，用于振动测量的加速度计十分有限，且多普勒激光测振仪(速度)几乎不可能，因此给其载荷辨识带来很大困难。

最近，光纤光栅应用的兴起，提供了轻量、串联复用、抗干扰的结构动应变响应测试途径式。然而，应变响应和结构载荷之间关系并不直接，需通过应变与位移间的关系间接建立。应变到位移是一个空间积分过程，在实际过程中测点数量有限，积分结果误差很大。目前结构位移模态和应变模态的识别方法都有一些成熟的方法，许多学者也推导了应变模态和位移模态的关系[10-12]。本文主要围绕基于应变响应的冲载荷识别进行研究，综合利用结构的位移模态和应变模态参数实现应变到位移的转换避免空间积分，稳定、精确地通过应变反求出了位移响应，进而实现了基于应变响应的识别。

1 基于位移响应的载荷识别

描述多自由度振动系统的方程为

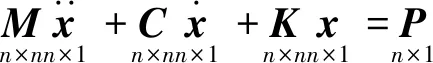
(1)

令Φn×m为系统质量归一化后的振型矩阵，同时假设阻尼为比例阻尼。

根据振型叠加原理

xn×1=Φn×mqm×1

(2)

式中：q为模态振型坐标，代表各振型在振动系统的贡献度。

将式(2)代入式(1)得

(3)

(4)

得到第j振型坐标下的振动方程

(5)

(6)

将式(6)代入式(2)可得在时刻的动响应

(7)

进一步可得

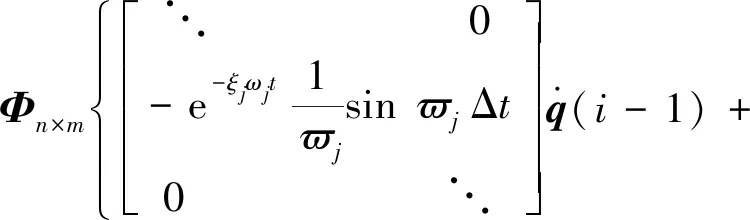
(8)

令

式(8)可改写为

(9)

由于振型坐标下的响应无法直接获得，需要将物理坐标下的位移响应转换到振型坐标下，根据式(2)可得

(10)

(11)

将式(10)代入式(9)可得

(12)

整理得

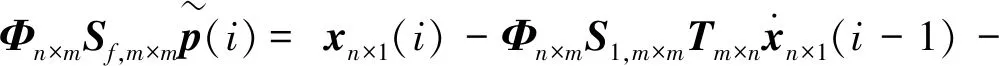
(13)

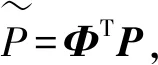
(14)

速度信息仍由位移响应采用五点差分得到

(15)

2 基于应变响应的载荷识别

应变响应相较于位移响应对载荷更加敏感，在识别瞬态载荷时识别精度更高。同时应变的测量也比位移测量简便。若利用应变响应进行载荷识别，需建立载荷到应变的关系。一般来说，两者通过位移相联系，应变到位移是一个积分过程，实际工程中测点有限，无法通过应变积分得到位移。

本文的基本思路是：通过试验或有限元数值仿真得到结构的位移模态和应变模态，找到应变和位移的关系，实现应变到位移的转换。

设弹性结构的变形位移分别为u，v和w，根据模态叠加原理得

(16)

(17)

(18)

式中：qr为时间和频率的函数，它代表的是各阶模态在结构变形中所占的比例，与坐标无关，因此∂qr/∂x=0。当然，根据上述推导方式，还可以推导出εy，εz以及γxy，γyz，γxz等表达式。

在三维空间中，设位移向量为x=[uvw]T，则位移模态为

(19)

根据弹性力学基本原理，应变与位移之间的关系为

(20)

式中：εx，εy和εz为正应变，剪应变为γxy=αyx+αxy，γyz=αzy+αyz，γzx=αxz+αzx。

根据模态叠加原理，得到应变张量响应表达式

(21)

考虑到利用应变计或FBG传感器测量结构应变时，通常只能测量结构正应变，因此，只考虑正应变时，则有

(22)

通过比较式(22)和式(19)可以发现，位移响应和应变响应拥有相同的模态坐标qr，因此，对于同一阶模态对应的振型，位移响应与应变响应具有相同的贡献度。

位移响应和应变响应拥有相同的模态坐标，因此有

(23)

(24)

(25)

式中：ψ和Φ分别为结构的应变模态和位移模态；Qε和Qx分别为应变模态坐标和位移模态坐标，可由最小二乘法解得模态坐标

(26)

由于Qε=Qx，所以得出

(ψTψ)-1ψT·ε=(ΦTΦ)-1ΦT·x

令Sε=(ψTψ)-1ψT，Sx=(ψTΦ)-1ΦT

Sεε=Sxx

(27)

根据最小二乘法可得应变到位移的转换关系

x=ΦSεε

(28)

为了缓解求逆过程时的矩阵病态，对方程进行正则化，引入正则化矩阵β，令Sε,β=(ψTψ+β)-1ψT得

x=ΦSε,βε

(29)

当以应变响应作为识别依据的时候，根据位移应变关系得

(30)

值得注意的是在应变-位移转换过程中，必须保证应变测点nε,d≥m，从而保证式(28)在正定或超定条件下求解。

3 正则化方法及参数选取

一般在对式(14)和式(28)进行求解的时候采用传统的最小二乘法就可直接求解。但是当系统矩阵条件数太大时，系统矩阵病态，会导致反求结果失真。此时需要采用正则化方法来缓解模型的不适定性。

本文参考文献[13]采用的是扩展Tikhonov方法。以一个一般的线性系统为例

AX=Y

(31)

(32)

(33)

正则化参数λ是平衡正则解的稳定性和精度的重要因素，λ过大精度低，过小则不稳定。

确定正则化参数在噪声水平未知的情况下一般有L曲线法和广义交叉验证准则，但是在实际应用时，L曲线常出现曲线不明显，参数不好选择的情况。所以本文采用广义交叉验证准则选取。其形式为

(34)

值得注意的一点就是若其中A是一维向量时，则采用广义交叉验证准则确定的正则化参数始终为0，即此时正则化方法无效，此时需要滤波等手段提高系统的鲁棒性。

本文在对式(14)和式(28)进行正则化时均采用上述方法。

4 海洋卫星的冲击载荷识别

为了对所述方法的正确性性和数值特性进行论证，本文根据文献[14]建立了海洋一号(HY-1)卫星的有限元模型，并尝试对它进行载荷辨识。

模型结构材料都采用碳纤维蜂窝复合材料(除了对接环)，各板之间采用刚性连接，电子设备采用非结构质量模拟，太阳能帆板采用集中质量模拟。

如图1所示在卫星的侧板施加单点瞬态载荷，载荷形式为

F=2 000sin(π/0.002t),t≤0.02 s

采用有限元软件Nastran得到卫星的位移模态和应变模态以及动力学响应，测量的位移为各节点上的位移，测量的应变为各单元中心。

图1 海洋卫星有限元模型Fig.1 Oceanic satellite finite element model

4.1 基于位移响应的识别

工况描述：模拟卫星在轨时受冲击情况，卫星受到一个垂直于板面的锯齿波载荷作用(单点激励)，载荷作用时间0.04 s，模型不受约束。

单点激励时，式(14)中的FI只有一个奇异值，矩阵条件数为1，矩阵呈良态，无需正则化，令α=0。

从图2可以看出，在测量响应中无噪声时，所建立的载荷识别模型能够很好地对所作用的冲击载荷进行识别。

从图3可以看出绝对误差在开始阶段会出现一个极大值，然后迅速稳定在某一水平上。开始时误差产生极大值的原因是：采用五点差分格式导致速度从第三点开始计算，而前两点是通过直接线性插值，速度误差较大。由于是非递推关系，所以此误差不存在积累，识别结果的精度在起始几点后仍得到保证。误差方向相反大小相等是由于识别模型假设时间步长内载荷不变，所以一直存在一个与斜率相关的误差，载荷斜率方向改变所以误差方向也随之改变，用更高阶的多项式来近似时间步长内的载荷可以减小该误差。

图2 无噪声识别结果Fig.2 No noise recognition results

图3 无噪声时识别绝对误差Fig.3 Absolute error of no noise recognition

4.2 基于应变响应的识别

整个模型共4 786个节点，选取150个单元中心的应变值作为测点数据，选取包含载荷作用点在内的50个节点的位移模态信息进行识别。

矩阵ψ的条件数为204.635 9远大于1，矩阵病态需要引入正则化参数λ。

从图4可以看出所述的应变位移转化关系能够在极小的误差范围内将应变响应转化为位移响应。

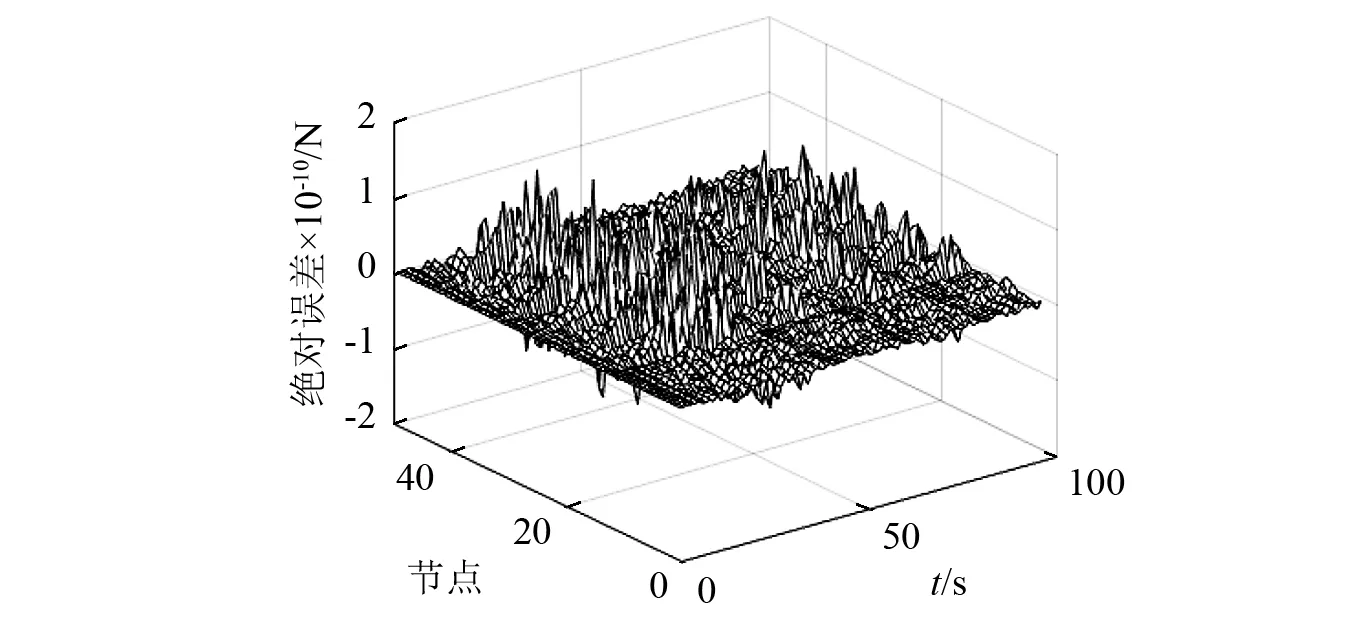
图4 无噪声正则化时转化过程绝对误差Fig.4 Absolute error of conversion without noise and regularization

从图5中可以看出当测量的响应信号中存在噪声干扰时，由于矩阵的病态会导致结果误差较大，影响了识别结果精度。所以需要引入正则化对噪声进行抑制，采用n=3的扩展Tikhonov正则化再根据广义交叉验证准则确定正则化参数为0.334 8，结果如图5所示。

对转换关系式进行正则化后，图6显示误差稳定在了一个很小的范围内，没有出现失真现象，即通过应变响应的识别结果与直接通过位移响应的识别结果基本一致，识别精度都很高。

图5 信噪比20 dB未则化时转化绝对误差Fig.5 Relative error of conversion with 20 dB signal-noise ratio without regularization

图6 信噪比20 dB正则化后转化绝对误差Fig.6 Relative error of conversion with 20 dB signal-noise ratio with regularization

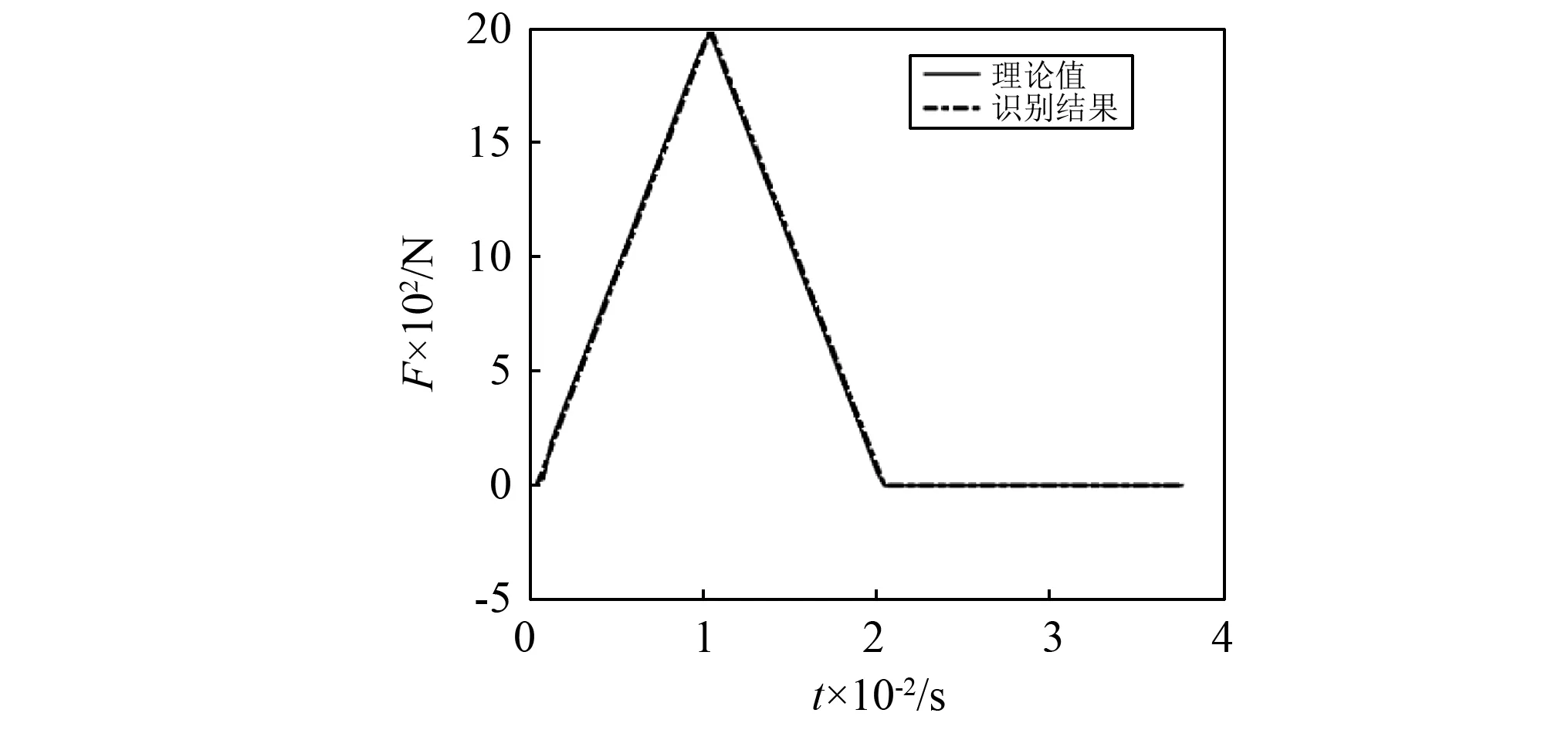
图7 无噪声时基于应变响应的识别结果Fig.7 Noise-free identification result based on strain response

从图8可以看出识别结果严重失真主要原因有两个：

(1)速度采用差分得到，会引入高频干扰，虽然在对应变—位移的转换过程进行正则化后会降低噪声的干扰，但是速度差分后会重新引入高频噪声。

(2)单点激励时式(30)中FI的只有一个奇异值，本例中FI的奇异值为5.743 9×10-9,由奇异值分解理论得

(35)

由于奇异值很小导致噪声误差被放大导致结果失真。

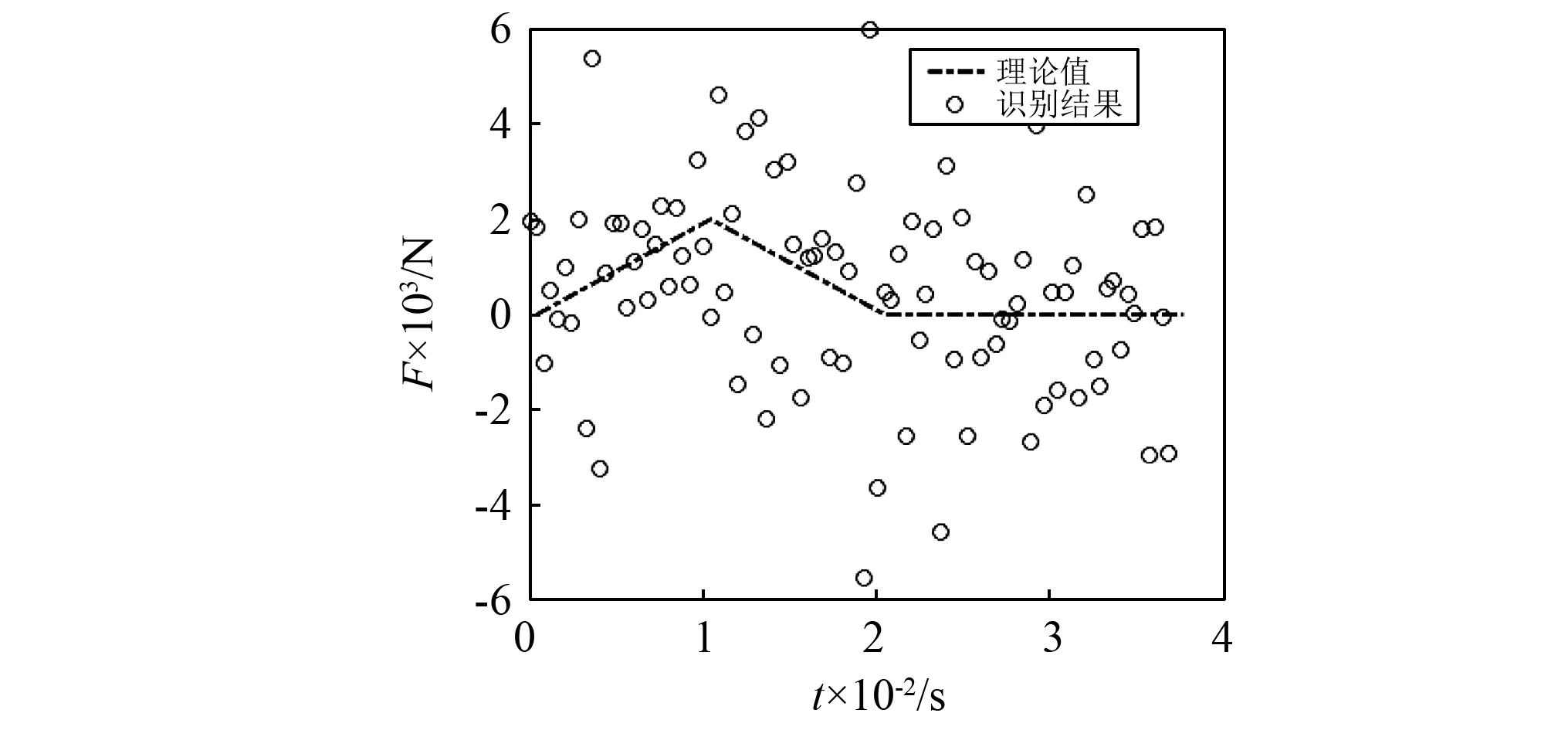
图8 信噪比20 dB时识别结果Fig.8 Result with regularization when signal-noise ratio is 20 dB

单点激励时，小奇异值引起的误差由于只有一个奇异值无法通过正则化减小，只有减小响应中的噪声误差err项。减小响应中的噪声误差只有引入滤波，本文采用八阶的最小二乘平滑滤波对由应变转换得到的位移响应进行滤波后进行识别结果，如图9所示。

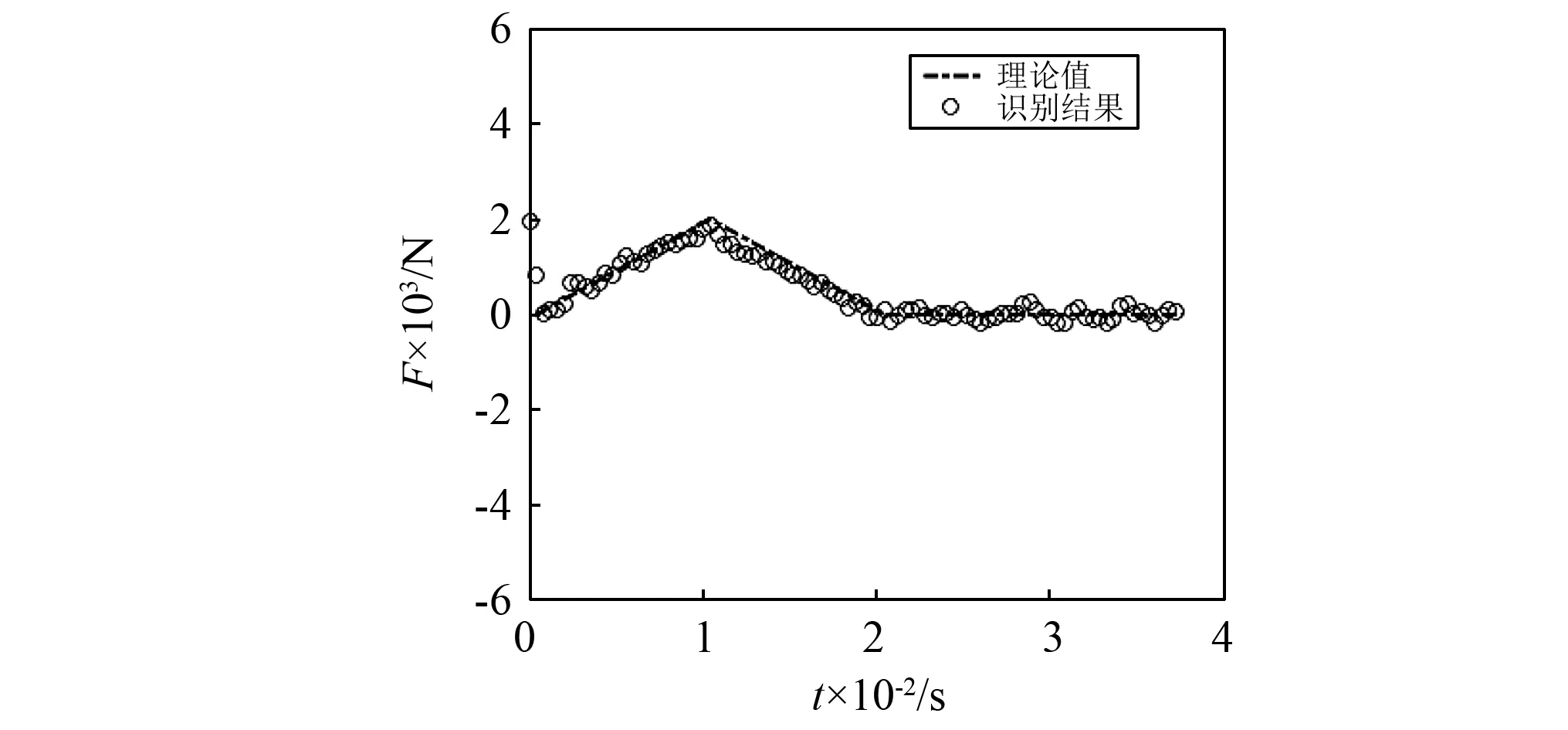
图9 信噪比20 dB时滤波后识别结果Fig.9 Result without regularization when signal-noise ratio is 20 dB

从图9可以看出当对转换得到的位移响应进行滤波处理后，识别结果基本处在了理论值附近，大大提高了识别进度和识别模型的鲁棒性。同时也得出当载荷作用点较少时，或是系统矩阵虽然条件数不大但是奇异值均较小时，采用正则化的处理对噪声的抑制作用不大，此时需要引入滤波方法对响应进行处理。

5 自由梁的锤击载荷识别

为了验证所述方法在实际中的应用，本文设计了如图10所示的自由梁实验装置，梁的基本参数为长1 200 mm,宽65 mm,厚4.5 mm，密度为7 850 kg/m3,弹性模量为210 000 MPa,泊松比为0.33。利用橡皮绳将梁竖直悬挂以近似自由-自由约束，在梁的一侧均匀布置13个FBG传感器记录传感器应变响应。该梁的位移模态和应变模态信息如表1 和表2 所示。采用力锤敲击梁未布置传感器的一侧与传感器相对的位置，并记录力的数据。实验结果如图11所示，识别结果如图12所示。对信号进行滤波时仍采用平滑滤波，但是在靠近峰值时滤波效果逐渐减弱，以减轻滤波对冲击响应幅值的影响。

图10 实验装置图Fig.10 Experiment equipment

特征频率/Hz位移模态振型16.61045.77689.717148.270

表2 位移模态信息

从图12可以看出识别出的锤击力的大小和作用时刻与测量的力信号基本一致，作用时间由于噪声影响较实际偏长。实际中对瞬态冲击响应的幅值和作用时刻更为关心，所以本文方法在实际中仍有很好的价值。

图11 锤击点应变响应Fig.11 Strain of the impact point

图12 识别结果与测量得到的力信号Fig.12 Identification result and measured force

6 结 论

本文所提方法主要是基于结构的应变模态参数和位移模态参数，运用应变响应来识别载荷。一方面由于光纤光栅的广泛应用，运行飞行器的多通道动应变响应测量进入实用化，因此利用多应变完成飞行器结构载荷识别成为可能；另一方面，通常应变响应对低频载荷更为敏感，基于应变响应的载荷识别无疑丰富了载荷识别的手段。

本文通过仿真与实验算例对所提方法进行了验证，结果表明：第一，方法利用应变响应，能够稳定高精度地识别结果瞬态载荷；第二，应用位移模态和应变模态实现应变响应到位移响应的转化，可以在很高的精度和稳定性下实现转换，而且过程简单、计算量小；第三，转化过程中存在矩阵病态问题所以需要引入正则化对其进行改善，正则化后在有噪声干扰时能够提高转化精度和数值稳定性；第四，识别过程由于采用差分求解速度会引入高频干扰，当系统矩阵维度减小时正则化对噪声的抑制作用减小，维度为1时正则化无作用，必须采用滤波方法提高识别的精度和鲁棒性。