高速破片穿透液舱的数值模拟研究

徐思博， 孟子飞， 刘文韬， 曹雪雁

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

高速破片作为武器爆炸攻击舰船的重要利器之一，其产生的高压环境难以测量，初始速度通常在1 000 m/s左右，其形状的随机性以及强穿透性，使得如何防护破片毁伤成为研究的难点。如今国际公认的防护手段是在舱壁外加设防护液舱用来衰减破片的冲击，研究水下近场爆炸高速破片在液舱中的衰减特性有极其重要的军事战略意义[1]。针对高速破片衰减特性，目前可行的方法主要有基于理想模型的数值验证和一些实验验证。高速破片击穿船舶液舱的整个过程大致分为冲击、拉伸、空穴形成和溃灭以及穿透内板四个阶段[2]。冲击阶段，破片接触液舱前壁并开始穿透，在舱壁后的液体内产生扰动；拉伸阶段，高速破片撞击液体并产生冲击波，之后在液体中前进；空穴的形成和溃灭阶段，高速破片在液体中的速度被迅速衰减，形成空穴并演化直至溃灭；穿透内板阶段，高速破片抵达液舱内壁并穿出。

穿透过程中有几个关键性的难点，包括：材料的动态力学性能和力学响应，高速破片水中速度衰减问题，水中冲击波形成的机理，空穴的形成和冲击波的叠加等。20世纪初期， Worthington等[3]用高速摄像机记录下圆球落水的动态过程中的飞溅和空泡现象，并以此为基础开启水弹道学的发展。我国在这项领域的研究开始于20世纪末期，仅做过少量的入水冲击、入水空泡实验[4-6]。陈先富[7]进行了不同形状弹丸入水的试验研究，记录了空穴的产生溃灭以及脉动，但由于试验工况较少，仅得出初始速度越高空穴增大越快这一结论。高速侵彻实验危险性大，实验条件要求高，同时随着计算机技术的飞速发展，对侵彻问题应用数值仿真方式进行模拟研究成为了解决该问题的有效且经济的途径之一。在21世纪，徐双喜等[8]依照破片穿甲运动方程以及德·玛尔模型，分析得出圆柱形破片穿透背水板的剩余速度公式，并采用Autodyn中的数值耦合算法模拟该过程，孔祥韶等[9]同时对双发破片的相互耦合作用模式进行分析，其主要研究为穿透后的剩余速度，并未涉及空穴演化等现象。Varas等[10]开展了低速以及高速下的球型破片击穿液舱的实验，并用高速成像仪记录下了高速破片形成的冲击波和空穴，并运用ALE算法进行了数值仿真，但弹片衰减速度、水中压力变化等仍有较大偏差。张婧等[11-13]则关注到多层防护结构及复合材料装甲加持下破片对结构的毁伤问题，与此同时沈晓乐等[14]在试验中对方形破片阻力系数进行修正，并通过试验研究破片的侵彻能力以及剩余特性。近几年，国内针对破片形状对侵彻的影响做了很多工作[15-17]，但并未引进新的仿真方法。杨文山等[18-19]则应用SPH方法对侵彻过程进行仿真，这种无网格光滑粒子在处理破口界面处有极好的模拟效果。

本文根据Varas等开展的球型弹片击穿液舱的实验数据，应用有限元软件ABAQUS中的CEL算法对该过程进行数值仿真。试验针对不同初始速度和装水量下的压力测点、空穴径宽、弹片速度衰减与实验数据进行对比，验证了CEL在模拟高速侵彻过程的适用性问题。

1 CEL算法的基本方程

CEL方法同时具有拉格朗日方法和欧拉方法的优势，较好的处理大变形、碰撞及一些流固耦合问题[20]。CEL在处理耦合问题中，应用拉格朗日算法计算结构以保持其在响应上的精度，用欧拉算法计算流体介质以解决其流动过程中的大变形问题。拉格朗日算法是一种离散化数值求解方法，其求解过程中，材料会依附在单元网格上，在网格的运动和变形的过程中伴随着材料的流动，计算过程中，单元会发生变形但单元的初始质量不变。具体控制方程为

(1)

(2)

(3)

式中:ρ,u,e,σ分别为拉格朗日流体介质的密度、速度、比内能和应力。

欧拉算法是一种固定网格而使材料在网格间运输的求解方法，计算过程中一个欧拉单元按用户定义的材料分配，有着不同的物质，整个计算过程中空间网格将会固定，而材料网格将以拉格朗日单元的状态变量实时传输到空间网格中，具体控制方程为

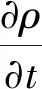
(4)

(5)

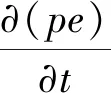
(6)

式中:ρ,u,e,σ,f分别为欧拉流体介质的密度、速度、比内能、应力和质量力。

在耦合算法之前，这两种算法是相互独立的，同时在耦合计算时通过耦合面的控制，欧拉的材料流动也不会穿透拉格朗日单元。耦合作用则通过在界面交换压力载荷和几何约束来实现，如图1所示。

图1 耦合界面处理示意图Fig.1 Coupling interface processing

2 高速破片穿透液舱的数值分析

高速破片穿透液舱的数值模型使用有限元仿真进行建立运算分析，符合工程应用背景以及科学研究需求。

2.1 液舱结构

鉴于有限元分析精准度与网格尺寸密切相关，为提高运算精度以及计算效率，仿真分析将采用实验整体模型的一半。根据Varas等实验中液舱的尺寸结构，液舱用6063-T5铝制成，长750 mm，宽150 mm，壁厚2.5 mm，液舱两侧用厚30 mm的PMMA有机玻璃封闭，在液舱内部设有两个压力测点PTn与PTf，液舱外部前后壁板设有应力及挠度测点G1与G2，测点位置如图4所示。破片为球形，直径12.5 mm，质量8 g，实验中选取600 m/s和900 m/s了两种初始速度。本次仿真针对该模型在壁厚方向(即弹片前进方向)设置3层网格单元，接近弹片侵彻位置附近皆为正六面体网格，网格尺寸为0.83 mm，最终液舱模型网格单元数为49 540个，如图2和图3所示。

仿真试验采用J-C模型描述液舱的本构关系。J-C模型的关系式为

(7)

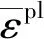
(8)

式中：θ为当前温度；θmelt为熔化温度；θtransition为转化温度。

在J-C失效模型中，断裂应变定义式为

(9)

表1 结构材料表

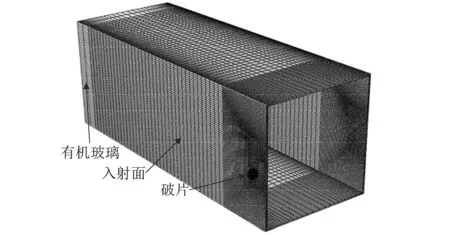
图2 液舱和破片数值模型Fig.2 Numerical modelling of fuel tanks and fragment

图3 破片入射面网格图Fig.3 Detail of the entry wall mesh

图4 压力测点位置示意图Fig.4 Sketch of pressure transducers

2.2 欧拉域

鉴于高速冲击问题带来的大变形以及流体的不规则流动，仿真试验将用欧拉网格建立水和空气的模型。在弹片穿透过程中，结构的大变形同时会伴随着流体的运动，因此欧拉域的设置应大于结构的区域以保证流体在流动过程中不会消失，保证能量守恒，所以欧拉域设置为190 mm宽。水和空气的材料属性通过体积分数方式离散进欧拉域内，最终欧拉网格单元数为4 061 300个，如图5所示。

图5 欧拉网格展示图Fig.5 Mesh of the fluids

水的状态方程采用Mie-Grüneisen状态方程，定义式为

(10)

式中：ρ0为流体密度；S，c0，Γ0为流体常数；η=1-ρ0/ρ。空气采用理想气体模型。水和空气的具体材料数据见表2。

表2 水和空气的材料参数表

3 数值计算结果分析

近场水下爆炸产生的破片速度通常在1 000 m/s左右，因此在本节中，将给出装水量75%和60%，弹片初始速度从600～1 200 m/s速度梯度下的工况数值仿真结果并与Varas等的实验数据进行对比，并分析装水量75%时不同入射速度下前后壁板应力及挠度对比。

3.1 破片高速侵彻过程

由仿真的结果可知，破片侵彻过程分为四个阶段，即冲击、拉伸、空穴形成和溃灭以及穿透内板，每个阶段在数值仿真中得到了充足的展现。在弹片穿透的瞬间，结构的应力峰值达到257 MPa，并沿冲击点向四周扩散圆形波，如图6(a)所示。在冲击阶段，当弹片穿透壁板之后，弹片的动能迅速在流体内形成高压的环境，并向四周扩散冲击波，如图6(b)所示。在拉伸阶段和空穴形成溃灭的阶段，弹片穿透水箱在流体内部留下一片空穴区，流体在惯性的作用下不断扩散使得空穴不断变化，而空穴溃灭所需时间远远大于高速弹片穿透水箱所需时间，如图6(c)所示。在穿透阶段，由于流体内冲击波预先到达壁板，弹片在到达之前就在壁板处产生预应力，图6(d)给出穿透阶段液舱的应力云图。

图6 初始速度900 m/s装水量75%的高速穿透过程Fig.6 HRAM phases in a tube impacted at 900 m/s and filled 75%

3.2 不同入射速度和装载量对破片速度衰减的影响

图7给出四组工况下速度衰减曲线与理论分析解和Varas等实验值得对比情况。可以看出数值分析方法CEL的结果与理论分析结果非常接近，只是CEL算法在弹片穿透液舱时会有较大的减速。由图7看出，CEL算法在弹片速度衰减趋势上与理论分析和实验有较好的拟合；由于弹片在液舱内滞留时间极短，液体阻滞作用有限，同时液面距弹道位置较远，液面效应较小，液舱内装水量对速度衰减趋势并没有影响；弹片在穿透入射面时速度大致衰减15%左右。

图7 速度衰减时历曲线对比(实验值与理论值源自Varas等的研究)Fig.7 Comparison of velocity decay vs. time (data of experiment and analysis come from Varas et al)

3.3 不同液体装载量对弹道空穴演化的影响

图8和图9给出由Varas等的实验数据中特定时刻空穴大小与CEL同一时刻空穴大小对比。可以看出CEL仿真结果与实验数据空穴大小、水面隆起的波高等十分接近。同时也发现，入射面与射出面的箱体呈现向外隆起的变形，由于穿透瞬间与弹片接触位置应力高达257 MPa，高于壁板的屈服应力使其瞬间形成穿透圆孔，而当弹片穿透之后，在内部流体的作用下，壁板所受应力维持在100～200 MPa，使液舱壁板进入塑性变形阶段发生屈曲却不至于形成断裂破损，而此时液体量的多少则是影响壁板屈曲变形的主要因素，如图8和图9所示，图中框线为液面初始位置。

液体装载量的变化决定了弹道距离自由液面的相对位置，并影响及导致弹道出现明显的非对称空穴现象，液体装载量从75%减小到60%，即弹道与自由液面的距离从6倍弹片半径减小到2.4倍弹片半径，非对称差异可由20%增加到48%，这种非对称差异导致空穴内压不平衡从而对弹道稳定性的影响很大。

图8 初始速度600 m/s装水量75%下空穴演化0.26 ms,0.46 ms,0.60 ms时刻实验数据与CEL算法数据的对比Fig.8 Cavity evolution at 0.26 ms, 0.46 ms, 0.60 ms obtained from experiments and CEL simulation for a tube impacted at 600 m/s, filled 75%

图9 初始速度600 m/s装水量60%下空穴演化0.13 ms,0.24 ms,0.38 ms时刻实验数据与CEL算法数据的对比Fig.9 Cavity evolution at 0.13 ms, 0.24 ms, 0.38 ms obtained from experiments and CEL simulation for a tube impacted at 600 m/s, filled 60%

3.4 不同入射速度对液舱隔板压力和变形的影响

根据实验中两个压力测点PTn，PTf与数值仿真结果进行对比，对比压力时历曲线如图10和图11所示。由于实验与数值仿真中弹片速度存在偏差，因此反映到压力时历曲线中对应出现峰值的时刻不尽相同，同时测点压力的峰值有所偏差，尤其是PTf，但两次压力峰值的脉宽十分接近，结果基本吻合；在Ptn测点，几次仿真结果均出现冲击波的二次加载，其峰值大致为第一次波峰的15%，两次波峰间脉宽小于0.05 ms，根据Ptn测点空间位置，推测二次加载为液舱底面反射稀疏波叠加形成(若是由射出面反射形成则脉宽应在0.12 ms左右，假定冲击波为球面波)。

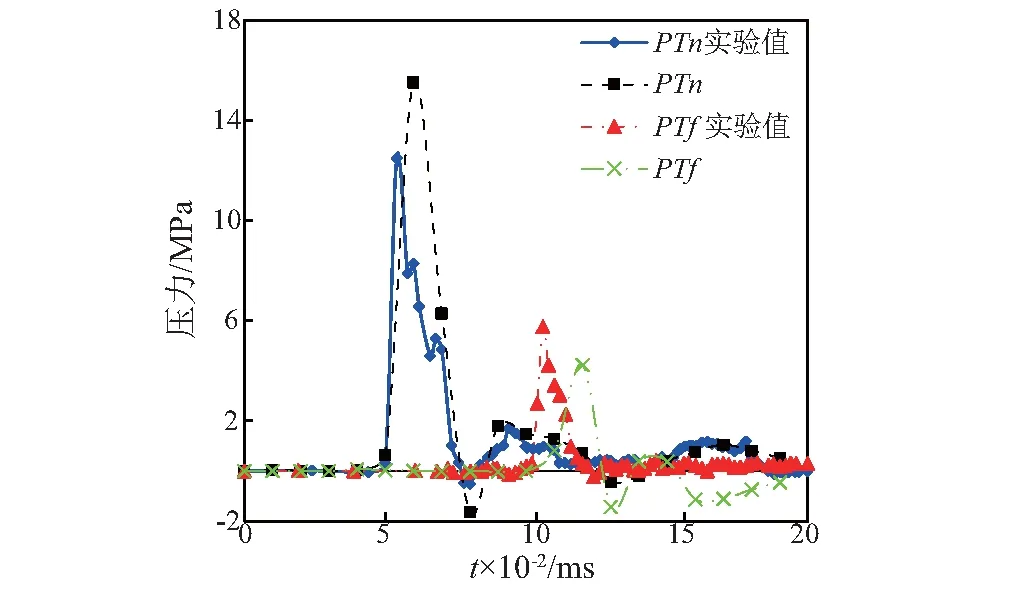
图10 装水量75%初始速度900 m/s的实验值与数值的压力时历曲线对比Fig.10 Experimental and numerical pressure time historyPtn and Ptf in a tube 75% filled impacted at 900 m/s

图11 装水量75%初始速度600 m/s的实验值与数值的压力时历曲线对比Fig.11 Experimental and numerical pressure time historyPtn and Ptf in a tube 75% filled impacted at 600 m/s

结构在达到塑性变形之前，分别经历线弹性阶段以及非线性弹性阶段，前置壁板在不同速度下应力响应如图12所示，不同入射速度下结构的应力响应仅因穿透时间不同而有一定的时域上的滞后性，而结构的应力响应只与材料本构方程有关，前置壁板在破片穿透过程中达到140 MPa左右应力，并在反射稀疏波抵达前置壁板前有一定的应力卸载，最终在稀疏波与水波的共同作用下达到动态屈服强度时应力达到最大值，此现象在后置壁板的应力响应中有更为明显的表现，如图13所示。图14给出在前后壁板测点位置最终挠度，随着初始速度的增加，前后隔板的变形挠度呈现出不同特征，即前置隔板的变形近乎呈线性关系，但幅度平缓，而后置隔板的变形呈非线性增长趋势。

图12 装水量75%不同速度下G1应力曲线Fig.12 Pressure time history G1 for a tube impacted at different velocity, filled 75%

图13 装水量75%不同速度下G2应力曲线Fig.13 Pressure time history G2 for a tube impacted at different velocity, filled 75%

图14 装水量75%壁板测点最终挠度Fig.14 Deflection in the end on the entry and exit wall of a tube impacted at different velocity, filled 75%

4 结 论

本文基于CEL算法研究了破片的高速侵彻问题，数值结果呈现出明显的四个阶段，即冲击、拉伸、空穴形成和溃灭以及穿透内板。文中首先以Varas等开展的高速弹片穿透铝制液舱实验为基础模型，验证了数值模拟结果的可靠性，进而模拟了不同破片速度、不同液舱装载量时高速侵彻过程的空穴演化特征，得出了以下结论：

(1) 在当前液舱参数下，弹片在穿透前置隔板时速度大致衰减15%左右；当弹道远离自由液面时，液舱装载量对破片速度衰减规律影响较小。

(2) 近自由液面入射弹道会出现明显的非对称空穴演化特征，随着与自由液面距离变小，非对称性差异可由20%增加到48%，这对弹道的稳定性影响很大。

(3) 随着破片初始速度增加，前后隔板的变形挠度呈现出不同特征，在当前速度范围内，前置隔板的变形随着破片入射速度增加而略有增加，但幅度平缓，而后置隔板的变形随入射速度增加呈非线性增长趋势。