考虑有限深度土体运动的Winkler地基梁自由振动分析

马建军, 秦紫果, 刘丰军， 高笑娟

(河南科技大学 土木工程学院, 河南 洛阳 471023)

弹性地基梁理论在土木工程中应用广泛，适用于条形基础、桩基础等结构的静动力学性能分析。为满足工程需要，国内外学者在弹性地基梁的建模理论和计算方法方面进行了深入研究，并取得了丰富成果[1-5]。其中，Winkler地基模型以其概念简洁、计算高效、结果准确等特点，在工程实践中应用最广泛[6-10]。

随着理论研究和工程应用的发展，Winkler地基梁的线性及非线性动力响应研究日益受到重视[11-14]。然而在已有的研究中，普遍用地基反力来表示Winkler地基对其支承梁的作用。在进行静力学分析时，这种简化方式是合理的，所得结果精确可信。但在进行动力学分析时，由于土-结构动力相互作用的影响，一定深度内的地基将与结构共同运动，此时土体运动对其支承梁的动力学特性将产生影响[15-16]。因此，有必要开展考虑土体运动的Winkler地基梁的动力响应研究。

本文拟基于经典Winkler地基理论，考虑有限深度土体运动的影响，建立包含地基运动的弹性地基上有限长梁的线性动力学模型。利用分离变量法，求解梁的运动微分方程，通过数值计算揭示弹性地基梁的自由振动特性，分析土体质量、地基深度、阻尼系数等对弹性地基梁动力学特性的影响，获得对工程应用有理论指导意义的结论。

1 计算模型

如图1所示，本文的研究对象为弹性地基上有限长梁，其中H为地基深度，L，b，h分别为梁的长、宽、高。为便于分析，以未变形梁的端点为坐标原点O，中轴线为x轴建立平面直角坐标系Oxy。p(x,t)=Pcosωpt为简谐动荷载，其中P和ωp分别为外激励幅值和频率。u(x,t)和v(x,t)分别为梁沿着x轴和y轴方向的位移，w(x,y,t)为有限深度弹性地基沿y轴方向的位移。

由于通常可忽略弹性地基梁类结构的轴向位移，本研究仅考虑其竖向位移v(x,t)。利用Winkler地基模型和Euler-Bernoulli梁理论，可得梁的线性运动方程

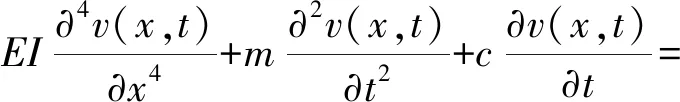
(1)

式中：c为单位长度梁的黏滞阻尼系数；q(x,t)为地基反力；m=ρA为单位长度梁的质量，ρ和A分别为梁的密度和横截面积；E和I分别为梁的弹性模量和惯性矩；∂/∂x和∂/∂t分别为对变量x和t的偏导。

图1 弹性地基梁模型Fig.1 Beam on elastic foundation

设地基土体为线弹性各向同性体，则有限深度Winkler地基的运动方程为

(2)

式中：ρs为单位长度梁下单位深度土体质量；cs为单位长度梁下单位深度土体的黏滞阻尼系数；kf为Winkler地基刚度系数；wr(x,y,t)为梁与地基间的相对位移。进而，地基反力可表示为

(3)

为便于分析，引入下列无量纲参数

(4)

将式(4)代入式(1)，可得梁的无量纲运动方程

(5)

式中：“′”为对变量x*的一阶导数；“·”为对变量t*的一阶导数。

同样，可得地基的无量纲运动方程

(6)

考虑梁与地基变形的连续性及工程实际，弹性地基位移w*(x*,y*,t*)应满足

w*(x*,0,t*)=v*(x*,t*);
w*(x*,H*,t*)=0

(7)

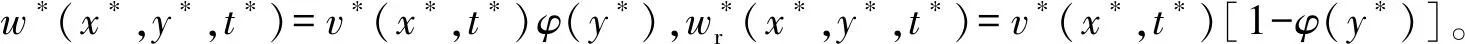
(8)

式中：γ为衰减系数，本文取γ=0.01。边界条件为

φ(0)=1;φ(H*)=0

(9)

将式(8)代入式(6)，并在y∈(0,H*)内积分可得

(10)

将式(10)代入式(5)，可得

(11)

其中，为便于表述，在式(11)及后续研究中均忽略无量纲参数的上标。

由式(11)可知，此时Winkler地基上有限长梁的运动方程中包含了地基质量、深度和阻尼系数等。显然地基运动对梁的动力学特性将有影响，有必要对其进行深入研究。

2 计算方法

为研究梁的自由振动响应，需略去式(11)中的外激励项。采用分离变量法，令v(x,t)=φ(x)Y(t)，则梁的自由振动是幅值按振动函数随时间变化，按模态构型φ(x)进行的运动[18]。可得

(12)

引入常数a4，可得

(13)

进而，可得常微分方程

φ′‴(x)-α4φ(x)=0

(14a)

(14b)

求解式(14a)，可得弹性地基梁第阶模态构型函数φi(x)的一般表达式

φi(x)=C1cosαix+C2sinαix+
C3coshαix+C4sinhαix

(15)

式中：C1～C4为待定系数。以弹性地基上固支-自由梁为例，其边界条件为

φ(0)=0;φ′(0)=0;φ″(L)=0;φ‴(L)=0

(16)

将式(15)代入式(16)，可得

[M]{Ci}=0, (i=1, 2, 3, 4)

(17)

式中：[M]为系数矩阵。

(18)

为求得非全为零的常系数Ci，令矩阵[M]的行列式为零，可得超越方程

1+coshαLcosαL=0

(19)

求解式(19)可得梁的第i阶固有频率ωi，相应的第i阶模态构型φi(x)为

φi(x)=C(cosαix-ξisinαix-coshαix+ξisinhαix)

(20)

式中：C为待定系数，可由模态构型规范化条件求得；ξi=(coshαiL+cosαiL)/(sinhαiL+sinαiL)。

由于弹性地基梁系统属于低阻尼体系，则振动函数Y(t)的一般表达式为

(21)

式中:G1和G2均为与动力响应初值相关的待定系数。经变换可得

(22)

进而，可得梁位移函数v(x,t)的一阶近似表达式

v(x,t)=a1(cosα1x-ξ1sinα1x-coshα1x+
ξ1sinhα1x)cos(ωD1t+θ)e-ηt

(23)

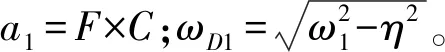
3 数值计算

为进行数值计算，表1给出了计算所需的梁和地基的尺寸和物理参数。

表1 梁和地基的尺寸和物理参数

3.1 方法验证

为验证本文正确性，在忽略土体运动影响的情况下与已有文献进行对比。以弹性地基上简支梁为例，梁的物理参数取表1中各变量值，弹性地基刚度系数为[19]：kf=16.55 MPa。表2给出了按文献[6，12，14，19]和本文方法求得的弹性地基上简支梁的前4阶固有频率。表2表明，由本文方法求得的固有频率与已有文献结果一致，表明本文方法正确。

表2 弹性地基上简支梁的固有频率

3.2 β的影响分析

利用表1中的物理参数，可得β=17.1，为分析其影响效应，计算时分别取β=0,β=5.0,β=10.0,β=20.0,β=30.0。表3给出了参数β取不同值时弹性地基梁的前5阶固有频率。由表3中固有频率随参数β的变化情况可知，若不考虑地基质量(β=0.0)的影响，计算出的各阶固有频率均较大；与实际情况(β=17.1)相比，各阶固有频率值均增大3倍以上。由此可知，若忽略有限深度地基运动的影响，求得的弹性地基梁系统整体刚度偏大。随参数β增大，系统的整体刚度逐渐降低，各阶固有频率相应减小。而且参数β增大到一定程度后，其对弹性地基梁系统固有频率的影响显著降低。此时地基质量在系统总质量中所占比例较大，弹性地基梁的动力学特性在一定程度上取决于地基的基本特征。

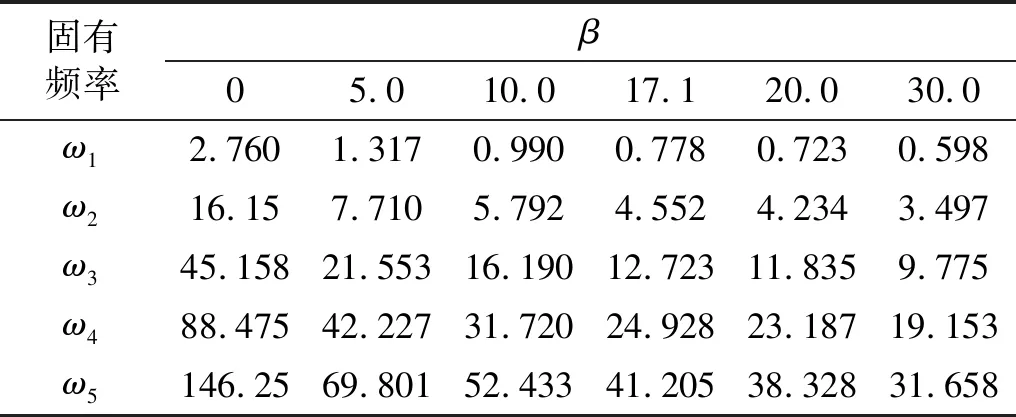
表3 参数β对弹性地基上梁固有频率的影响

令式(23)中θ=0，图2给出了Winkler地基上有限长梁中点处的位移时程曲线，其中参数β分别取为0，5.0，17.1。如图2所示，三种情况下弹性地基梁动力响应的周期分别用T1，T2，T3标注出来。对比可知，若将土体运动引入弹性地基梁的动力学模型，系统的响应周期将增长。理论上讲，这在一定程度上证实了土-结构动力相互作用效应能改善结构的抗震性能。由阻尼参数η定义可知，参数β的变化将引起η值改变。在t∈[150, 160]的某一临近时间段内，图2中用Δ1,Δ2,Δ3分别表示三种情况下梁中点处位移最大值与初始值间的差值。显然，参数β的增大将减慢响应幅值衰减速度，延长了有阻尼自由振动持续时间。

图2 参数β对位移时程曲线的影响Fig.2 Effect of parameter β on the midpoint displacement

3.3 λ的影响分析

由工程实际可知，结构静动力响应引起的土体位移或变形均随地基深度衰减。当地基深度达到一定值后，其下部土体的变形将十分微弱，可忽略不计。因此在对地基深度的影响进行分析时，仅考虑λ≤3.00的情况。

利用表1中的物理参数，计算可得λ=1.64，本研究仅由地基深度变化实现参数λ的改变。表4给出了λ=0.50,λ=1.00,λ=3.00时系统的前5阶固有频率。由表4可知，随参数λ增大，弹性地基梁的各阶频率均减小。由频率ω随参数λ的变化情况可知，在参数λ值较小时，其对系统动力学特性影响显著；当参数λ值较大时，其影响效应相对较弱。因此在计算分析时，结合实际情况仅考虑有限深度土体运动的影响即可。

表4 参数λ对弹性地基上梁固有频率的影响

图3给出了弹性地基梁中点处的位移时程曲线，其中参数λ分别取为0.50，1.00，1.64。如图3所示，随参数λ增大，弹性地基梁系统的响应周期增长。由于地基深度增加，参与到系统动力响应中的土体质量相应增加，图3中位移曲线的变化也符合参数β对系统动力响应影响的分析结论。对比响应幅值的衰减情况可知，若λ≥1.00，其对阻尼参数η的影响微弱，Δ2与Δ3之间的差异很小。

图3 参数λ对位移时程曲线的影响Fig.3 Effect of parameter λ on the midpoint displacement

3.4 η的影响分析

图4给出了弹性地基梁中点处位移时程曲线随参数η变化的情况，其中η=2.099×10-4为表1中参数计算所得。若η=0，则为无阻尼自由振动，弹性地基梁将发生响应幅值不变的稳态周期运动。对于低阻尼体系而言，参数η对周期T的影响非常微弱，可忽略不计。随参数η值增大，弹性地基梁动力响应幅值的衰减速度增快，即在相同时间点出现Δ3>Δ2的情况。可以预见，当参数η增大到临界值时，系统自由振动的时程曲线将呈单调衰减。

图4 参数η对位移时程曲线的影响Fig.4 Effect of parameter η on the midpoint displacement

4 结 论

本文基于Winkler地基模型，考虑有限深度土体运动的影响，建立了弹性地基上有限长梁的线性动力学模型，利用分离变量法计算了梁的固有频率和有阻尼自由振动响应，研究了地基质量、深度、阻尼等对梁动力学特性的影响。通过参数分析，得到如下结论：

(1) 随着与有限长梁动力响应相关的地基质量增大，Winkler地基上梁的固有频率减小，有阻尼自由振动响应幅值衰减速度减慢。

(2) 随着地基深度在有效范围内增大，Winkler地基上梁的固有频率迅速减小，但地基深度对系统阻尼效应发挥的影响较弱。

(3) 在合理的参数范围内，阻尼系数对Winkler地基上梁动力响应周期的影响可忽略不计，但对响应幅值衰减速度的影响非常显著。

另外，需要注意的是：本文模型仅适用于线弹性、理想化Winkler地基上有限长梁的动力响应分析，而未考虑地基主要参数随深度变化等情况。为促进研究及应用的发展，有必要继续进行考虑复杂地基条件下弹性地基梁的建模研究，以期精确分析有限深度地基上梁的动力学特性。