巧用均值不等式证明2018年数学奥林匹克不等式题
2019-04-01 10:57:46江西教育传媒集团330038
中学数学研究(江西) 2019年3期
江西教育传媒集团 (330038)
周瑜芽
均值不等式是一个应用广泛的不等式,在证明不等式问题时,为了创设使用均值不等式的条件,常常需要对题中的式子作适当的变形,而变形的出发点又是在兼顾所给条件的基础上注意不等式的取等条件,若遇到等号取不到、用“均值法”无效时可考虑引入参数,借助待定系数法来解决.这样才能使复杂问题简单化,从而达到事半功倍的效果.下面举例说明.
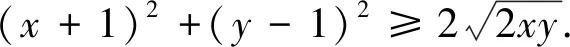
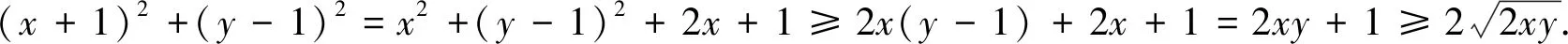
读者可以自己完成下面另一道2018年乌克兰数学奥林匹克试题的证明:
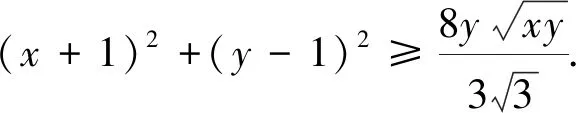
推广到三元,笔者编拟以下试题:
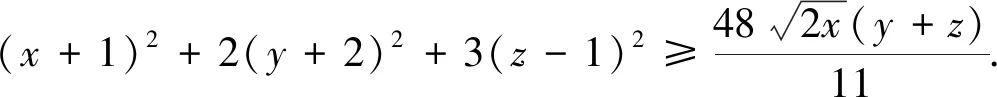
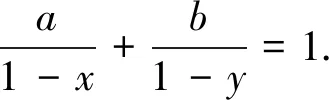
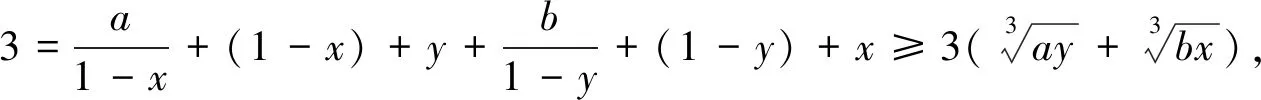
推而广之,我们有(证明留给读者):
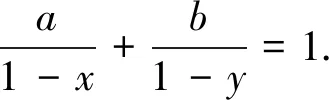

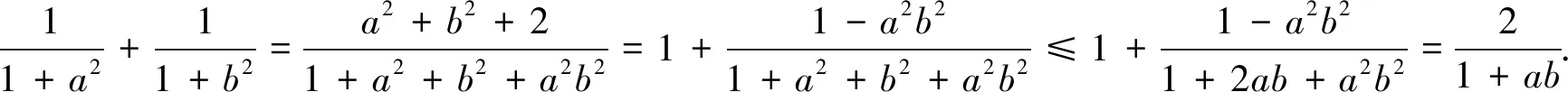
本题可以推广:



故原不等式成立.
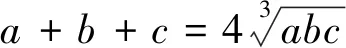
证明:不妨设min{a,b,c}=a,则原不等式成为2(ab+bc+ca)+4a2≥a2+b2+c2.

(a+b+c)2⟺2(ab+bc+ca)+4a2≥a2+b2+c2.
故原不等式成立.
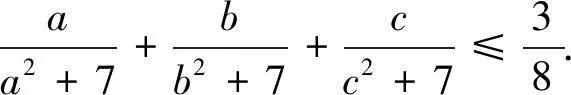
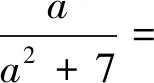


类似的不等式有(证明留给读者):
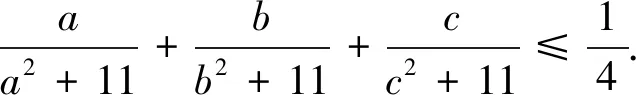
例7 (2018年香港数学奥林匹克)已知a,b,c是满足57a+88b+125c≥1148的正数,求a3+b3+c3+5(a2+b2+c2)的最小值.
解:由均值不等式,可得a3+b3+c3+5(a2+b2+c2)=(a3+33+33)+(b3+43+43)+(c3+53+53)+5(a2+32)+5(b2+42)+5(c2+52)-2(33+43+53)-5(32+42+52)≥3(32a+42b+52c)+10(3a+4b+5c)-682=57a+88b+125c-682≥1148-682=466,当a=3,b=4,c=5时,a3+b3+c3+5(a2+b2+c2)取得最小值466.
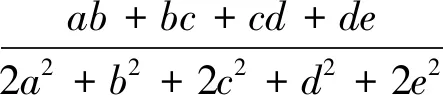
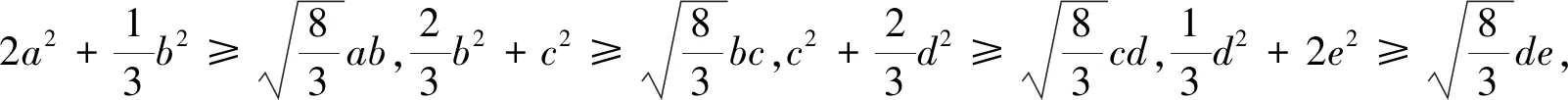
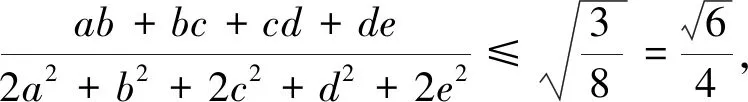
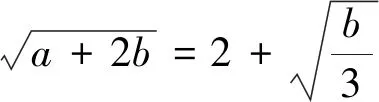
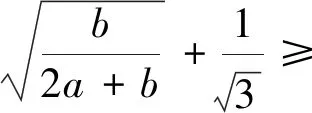
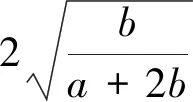
推而广之,我们有(证明留给读者):
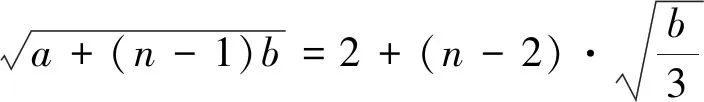
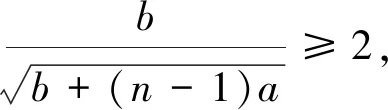
猜你喜欢
山西教育·招考(2021年5期)2021-11-30 12:55:43
山西教育·招考(2019年6期)2019-09-10 07:22:44
学生导报·初中版(2019年5期)2019-09-10 07:22:44
中学课程辅导·高考版(2019年4期)2019-04-25 00:25:02
小雪花·成长指南(2016年1期)2017-02-13 10:29:30
高中生学习·高三版(2016年1期)2016-05-30 05:45:06
小雪花·成长指南(2016年3期)2016-04-20 06:24:08
小雪花·成长指南(2016年2期)2016-03-16 06:38:56
中学生数理化(高中版.高二数学)(2016年4期)2016-03-01 03:46:20
浙江理工大学学报(自然科学版)(2015年5期)2015-03-01 02:54:01

