递推数列中的完全平方数分析*

重庆市第八中学 (400030)

罗 毅 李长江

完全平方数分析是竞赛数论中的常见问题，文[1]归纳了一些判断完全平方数的方法．而在近年的赛题中，还出现了以(递推)数列为载体的完全平方数分析问题，这类问题中，不仅涉及到完全平方数的性质研究，还需要借助递推数列的处理技巧，如构造、配凑、变阶等，形成别具一格的题型．本文针对这类问题，在解题方法上进行探究和归纳，以飨读者．

一、通项公式法

由递推关系求出数列通项公式，借助通项公式的结构特征，分析数列中的项是否是完全平方数．这种方法对低阶线性递推关系较为适用．

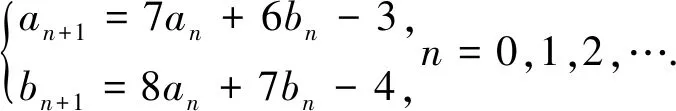
评注:本题条件化简之后是一个典型的二阶线性递推关系，容易通过特征根法求出其通项，借助二项式定理的结论即得．

例2 已知x0=1，x1=3，xn+1=6xn-xn-1(n∈N+)，求证：数列{xn}(n≥1)中无完全平方数．(《中等数学》2003年第3期训练题)

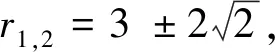
评注:本题求出{xn}的通项公式后，通过构造{xn}的对偶数列{yn}形成不定方程，转化为探求不定方程解存在性的问题．

例3 两个整数数列{an}与{bn}(n∈N)满足bn=an+9，an+1=8bn+8，(n∈N)．又1988是两个数列的公共项．求证：数列{an}中不含完全平方数的项．(1988奥地利—波兰数学奥林匹克)

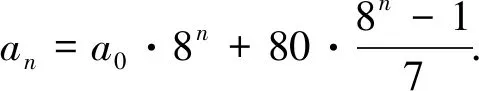
当n≥3时，an=16[4a08n-2+5(8n-1+8n-2+…+1)]．∵4a08n-2+5(8n-1+8n-2+…+1)≡5(mod8),所以an(n≥3)不是完全平方数．下验证a0，a1，a2都不是完全平方数．因为当n≥1时，8|an，且bn为奇数，所以an和bn均不为1988，因此必有a0=1988或b0=1988．

当b0=1988时，a0=1979，a1=8·1989，a2=8·(8·1989+10)=16·7961，均不是完全平方数；当a0=1988时，a1=8·1998，a2=16·(4·1988+45)，均不是完全平方数．

综上，命题得证．

二、构造转换法

对于不能或不宜求出通项公式的递推关系，可以考虑直接借助递推关系作构造，利用f(an,an+1,…)整体形成完全平方数(式)形式，实现证明．

1.择项构造

例4 给定正整数u、v．数列{an}定义如下：a1=u+v，对整数m≥1，a2m=am+u，a2m+1=am+v．记Sm=a1+a2+…+am(m=1,2,…)．证明：数列{Sn}中有无穷多项是完全平方数．(2013全国高中数学联赛加试第2题)

证明：对正整数n，S2n+1-1=a1+(a2+a3)+(a4+a5)+…+(a2n+1-2+a2n+1-1)=(u+v)+(a1+u+a1+v)+(a2+u+a2+v)+…+(a2n-1+u+a2n-1+v)=2n(u+v)+2S2n-1，所以S2n-1=n·2n-1(u+v)．取n=2(u+v)k2(k∈N+)，S2n-1=2(u+v)k2·22(u+v)k2-1(u+v)=(u+v)2k2·22(u+v)k2=[(u+v)k·2(u+v)k2]2．于是S2n-1为完全平方数．由于正整数k有无穷多个，从而原命题得证．

评注:这种解法巧妙的选择了数列{Sn}中第2n-1项作分析，在找到递推关系S2n+1-1=2n(u+v)+2S2n-1后求出S2n-1的通项公式，再通过取n的值实现证明．该解法由江苏常熟市中学查正开老师提供．

2.变阶构造

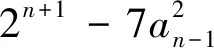
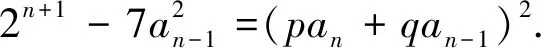
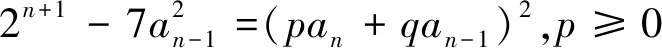
下用数学归纳法证之：

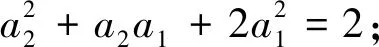
评注:本题条件中给出一个二阶线性递推关系f(an-2,an-1,an)=0，但其通项公式不易求取，而通过待定系数将所探求的表达式用g(an-1,an)=0表示，降阶整体构造出完全平方数形式．

例6 数列{an}满足a0=1，an+1=

(1)对于任意n∈N，an为整数；

(2)对于任意n∈N，anan+1-1为完全平方数．

(2005全国高中数学联赛)

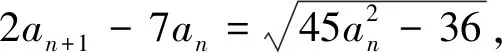
①-②得(an+1-an-1)(an+1+an-1-7an)=0，∵an+1>an-1，∴an+1=7an-an-1③.

由③及a0=1，a1=5可知对于任意n∈N，an为整数．

评注:将原条件中的一阶非线性递推关系升阶转化成二阶线性递推关系，其目的还是为了简化运算形式．

3.逆向转化

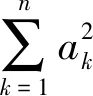
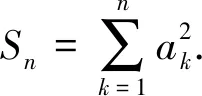
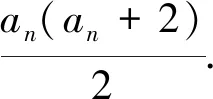
评注:本题的关键在于借助Sn与an的关系，反向构造an．

三、同余分析法

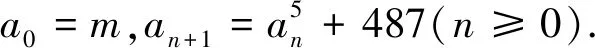
解：若an是一个完全平方数，则an≡0或1(mod4)．

①若ak≡0(mod4)，则ak+i≡

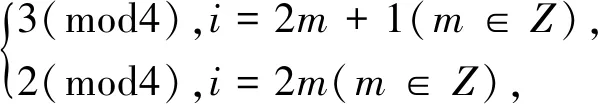
②若ak≡1(mod4)，则ak+1=0(mod4)．从而，当n>k+1时，an不是完全平方数．

于是，数列{an}中至多有两个完全平方数，设为ak和ak+1．令ak=s2(s为奇数)，则ak+1=s10+487=t2．

设t=s5+r，则t2=(s5+r)2=s10+2s5r+r2，从而2s5r+r2=487．

若s=1，则r(r+2)=487，该方程无整数解；

若s=3，则486r+r2=487，解得r=1，r=-487(舍去)；

若s>3，该方程显然无正整数解．从而ak=9．而当n>0时，an>487，故m=a0=9．

另一方面，当a0=9时，a1=95+487=2442是完全平方数．

综上，所求m=9．