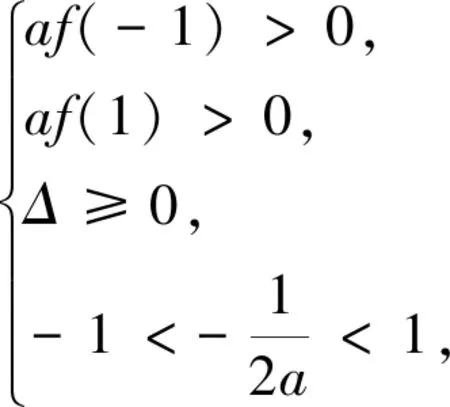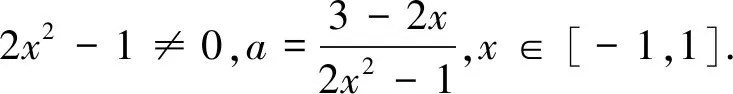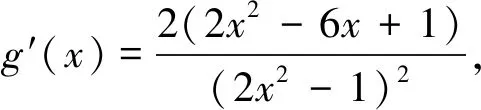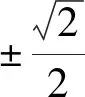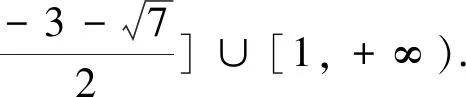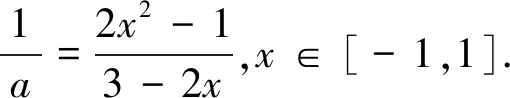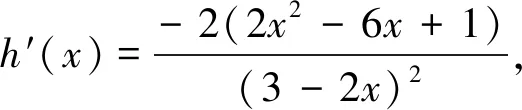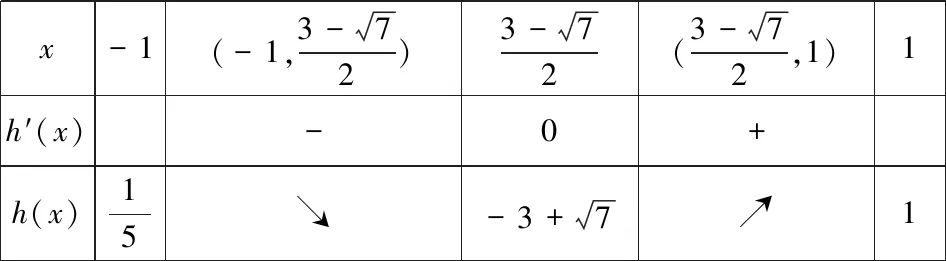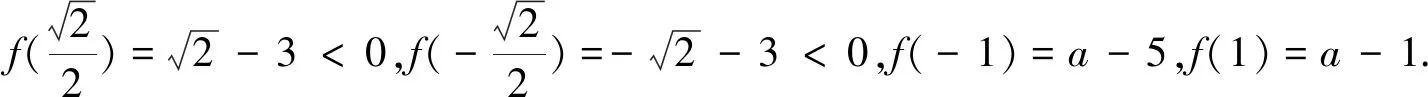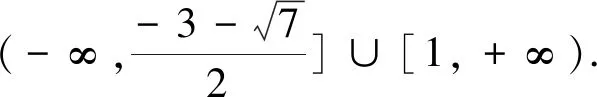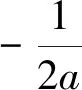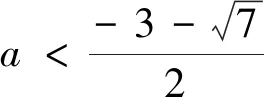一道函数零点题的解法剖析
安徽省灵璧师范学校 (234200)
陈 伟
在解题过程中,尝试不同的视角分析解决同一个问题,可以强化知识间的联系,提高学生运用知识分析问题和解决问题的能力.本文结合一道函数零点题,剖析其多种解法,探讨解决函数零点问题的基本思路方法.
题目已知a是实数,函数f(x)=2ax2+2x-3-a.如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.(2007年广东省高考题)
法一、二次函数零点分布

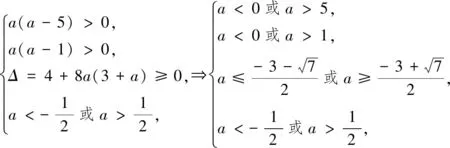
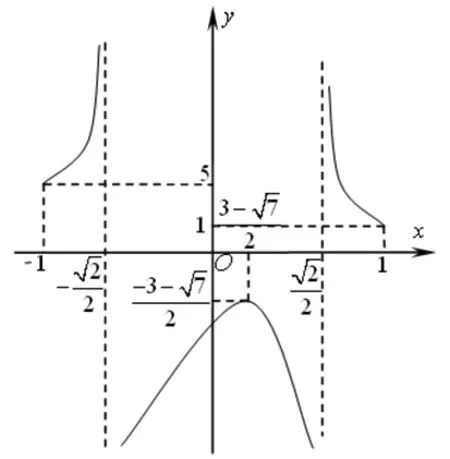
[-1,1],所以a≠0.
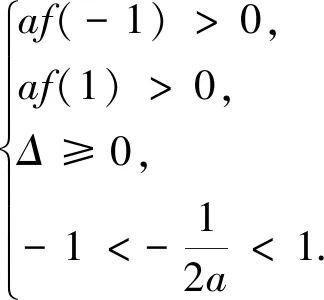
由f(-1)f(1)<0,即(a-5)(a-1)<0,
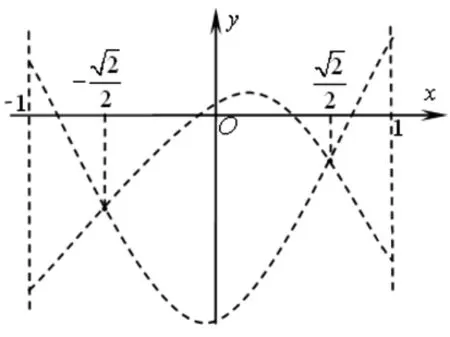
得1 法二、参数分离法 解:函数y=f(x)在区间[-1,1]上有零点,等价于关于x的方程2ax2+2x-3-a=0在区间 [-1,1]上有解,即关于x的方程a(2x2-1)+2x-3=0在区间[-1,1]上有解. 列表如下: x-1(-1,-22)(-22,3-72)3-72(3-72,22)(22,1)1g′(x)++0--g(x)5↗↗-3-72↘↘1 图1 也可采用如下参数分离法来解题. 函数y=f(x)在区间[-1,1]上有零点,等价于关于x的方程2ax2+2x-3-a=0在区间[-1,1]上有解,即关于x方程a(2x2-1)+2x-3=0在区间[-1,1]上有解. 列表如下: x-1(-1,3-72)3-72(3-72,1)1h′(x)-0+h(x)15↘-3+7↗1 法三、数形结合法 图2 ②当a>0时,二次函数y=f(x)图像开口向上,若在区间[-1,1]上有零点,则f(-1)≥0或f(1)≥0,得a≥1; 法四、正难则反 解:若函数y=f(x)在区间[-1,1]上没有零点. [-1,1]; ②当a>0时,二次函数y=f(x)图像开口向上,若在区间[-1,1]上没有零点,则f(-1)<0且 f(1)<0,得0 ③当a<0时,f(-1)<0且f(1)<0,二次函数y=f(x)图像开口向下,若在区间[-1,1]上没有零点,则二次函数y=f(x)图像的对称轴x= 变式训练已知a是实数,讨论函数f(x)=2ax2+2x-3-a在区间[-1,1]上的零点个数.