突破函数压轴题的瓶颈——如何选择ex、lnx、sinx结合的综合题处理方法

江苏省吴县中学 (215151)

唐俊涛

高考函数的压轴题往往是以ex,lnx,sinx做为载体，命题者对这类型的函数“情有独钟”，几乎年年各地的高考试卷中都会出现.若题目将它们结合在一起，那就更具灵活性，这对解题者的数学技能及数学抽象等要求将更高.所以这样的函数题就成了数学高考的难点及热点.本文通过几种常见处理该类题目的方法进行总结，希望对大家有所帮助，同时也希望得到各位专家同仁的指导.

一、整体“讨论”，正面求解

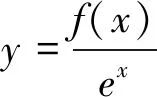
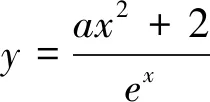
本题属于常规题型，学生在解题过程中只需牢记导数用于处理函数单调性的方式方法即可：

(1)求函数单调区间时，应该令函数导数f′(x)>0(增区间)或f′(x)<0(减区间)；

(2)函数f(x)在区间内单调，则应该满足f′(x)≥0(≤0)在给定区间恒成立来处理解决.

例2 已知函数f(x)=xlnx-aex有两个极值点，求实数a的取值范围.

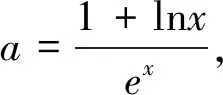
点评：这两题的切入口都较为简单，直接从正面分析后就能得到解题思路，例1将问题最终转化为了二次函数恒成立问题，而例2从正面求导运算后，在判断导数为零的方程时遇到困难，但是通过分析思考后，可将原来的导函数进行“分离参数”，而后判断两个函数图像的交点个数来解决此类问题，这两题都属于常规直接正面解决的问题.

二、分开“判断”，双管齐下

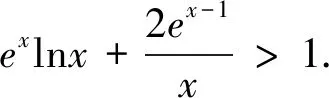
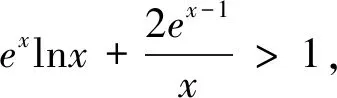
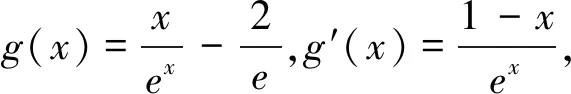
例4 已知函数f(x)=xlnx,g(x)=-x2+ax-3.

(1)对一切x∈(0,+∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；

解析：(1)分离参数，构成新函数，然后通过对新函数求最值来求解；

三、分离参数，极端原理

利用导数研究不等式恒成立问题，首先要确立研究函数，通过导函数研究该函数的单调性，求出最值，进而得出相应的含参不等式，从而求出参数的取值范围；当然也可以分离参数，构造新函数，利用“极端原则”，直接把问题转化为求新函数的最值问题.

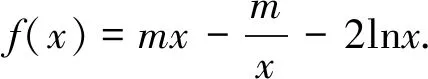
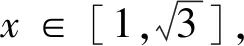
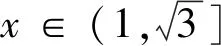
在解此类型题目的时候，我们一般是分三个步骤：一是分离参数，得到a≥f(x)或a≤f(x)；二是求函数f(x)的最值，得到f(x)max或f(x)min；三是极端原理，即a≥f(x)max或a≤f(x)min.由于第一步分离参数后，就不用再担心不等式左右的x不一致了.

四、切线“放缩”，层层递进

由于ex,lnx的存在使得函数很难进行处理，所以我们有时也可以利用“切线”不等式(ex≥x+1(x=0取等号)，lnx≤x-1(x=1取等号),sinx≤x(x=0取等号)),从而将函数或不等式中的ex,lnx,sinx都变为了更容易处理的一次函数，让问题的处理出现了“柳暗花明又一村”的境界，让解题过程简洁明了.

例6 函数f(x)=xex-a(lnx+x).(1)略；(2)若对任意x>0恒有不等式f(x)>1成立.①求实数a的值；②证明：x2ex>(x+2)lnx+2sinx.

解析：(1)略；(2)a=1；②要证明x2ex>(x+2)lnx+2sinx，只需要证明x2ex-(x+2)lnx-2sinx>0,因为x>0,所以ex>x+1,lnx≤x-1,sinx(x+2)lnx+2sinx.

这题的处理就是借助于三个常见的“切线”不等式(ex≥x+1(x=0取等号)，lnx≤x-1(x=1取等号),sinx≤x(x=0取等号),摆脱了ex、lnx、sinx这样复杂的混合式，将复杂的不等式转变为我们极其熟悉的三次不等式，最终完美简答，这样的题目思考的过程是“痛苦”的，但是结果是顺畅的，也让人感觉了数学的奇妙性.

例7 已知函数f(x)=ex+m-x3,g(x)=ln(x+1)+2.求证：当m≥1时，f(x)>g(x)-x3.

解析：f(x)>g(x)-x3等价于ex+m-ln(x+1)-2>0.由于m≥1，所以上式只要证明ex+1-ln(x+1)-2>0即可，有切线不等式ex+1≥x+2,又可以将上述不等式转化为：证明x+2-ln(x+1)-2>0,即只需证明x-ln(x+1)>0.下面就比较简单了.

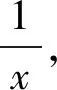
五、运用“图像”，数形结合

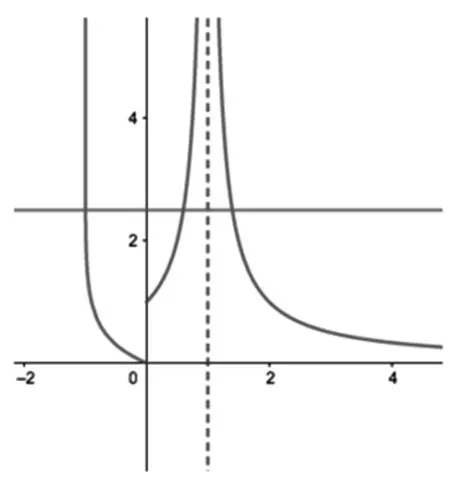
图1

解析：本题的入手应该比较明朗，通过两个函数图像交点最终求零点范围问题，在作函数f(x)的图像时，如图1，首先先画x≥0的图像，y=

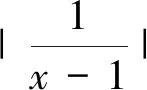
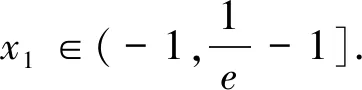
可见本题的关键就是在于图像，而图像中需要注意的是那些渐近线.数形结合是高中阶段重要的思想方法，学生可以通过转化化归的方法将陌生的函数转化为我们熟悉的函数，然后在利用熟悉函数的图像对现有的问题进行观察思考，从而寻求解题的途径，虽然图像法不能直接应用在解答题中，但是填空题中还是可以借助图像来解决问题的，当然图像法也可以帮助我们对问题进行思考分析.

六、构造“函数”，顺流而下

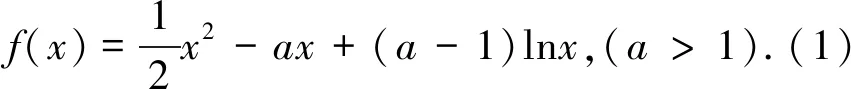
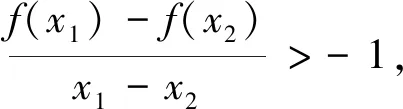
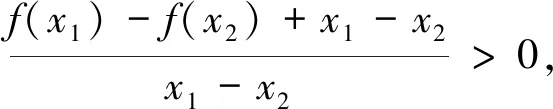
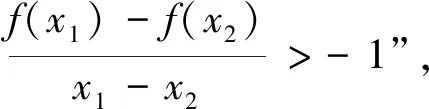
例10 已知函数f(x)=ex(2x-1)-ax+a(a∈R),e为自然对数的底数.

(1)当a=1时，求函数f(x)的单调区间；

(2)①若存在实数x，满足f(x)<0，求实数a的取值范围；②若有且只有唯一整数x0，满足f(x0)<0，求实数a的取值范围.

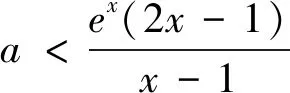
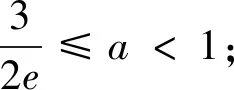
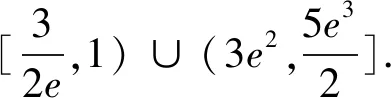
分析：在证明不等式时，通常需要根据不等式的特点将已知不等式进行适当的变形，构造出新函数，用导数解决函数问题，此类问题变化多，思路广，但是核心点在于构造函数，构造的新函数需要是熟悉常见的，方便下一步的处理.

压轴题由于位置的特殊性，解题时往往需要用到对称分析、结构分析、图形化、数学技巧、思想等等.教师在评讲练习时，由于事先已经做好准备，进行了思考分析，所以讲解后学生总认为解题的解法是一种必然的结果.但是学生自己处理问题时总觉得无从下手，像“无头苍蝇到处乱撞”.所以笔者认为解题时应该注意解题的感觉，少谈一些原则，解题最好的办法就是探索，提高解题能力的捷径是反思总结.学生经常反映：“做了很多的题目，解题能力为何并没有提升？”这多半可能是没有做好及时的总结，做完一道有难度的题目，一定要回顾一遍，弄清：解本题需要哪些步骤，哪些必须，哪些多余，哪些关键，哪些易得，有无更好的方法.所以总结是提高解题能力的重要环节.

教师的课堂任务并不是教学生解题，而是要教会学生如何去发现解题的路径，讲到解题那就不得不说伟大的数学家波利亚，他的很多思想理论不是教条，而是实际解题的指南，平时也可以给学生灌输一些他的经典理论，让学生自己去体会这些理论，同样也能够提高自身的解题能力.数学复习课的提升点就在于有效地将多个板块的知识点进行有效地整合，将知识点、课后练习、模拟题、高考题有机地结合起来，理清它们之间的联系，让课堂教学更加有效地激活学生的思维.从而提升学生对数学的感觉、对数学的理解，提高复习课堂的效率.

复习备考中，笔者认为必须做题，只有“跳入题海，才能畅游题海”，但是做了题、讲了题之后必须要花点精力去精心反思总结、分析透彻，才能触类旁通.高考压轴题是由多个知识板块“揉捏”而成的，如果学生能够准确的找到题目中问题的本质，那么高考压轴题也能够容易的突破了.