基于PCA与DBN的航空发动机气路系统故障诊断

蒋丽英,栗文龙,崔建国,于明月,林泽力

(1.沈阳航空航天大学 自动化学院 ，沈阳 110136；2.航空工业上海航空测控技术研究所故障诊断与健康管理技术航空科技重点实验室，上海 201601)

航空发动机作为一个复杂的高转速机械系统[1]长期工作在高温、高压、强腐蚀和高密度能力释放等恶劣的高空环境中，极易受到侵蚀和外来物体打伤等，轻则导致发动机故障发生，重则将会造成飞机毁灭性破坏。针对飞机发动机气路系统的故障诊断问题国内外相关研究人员提出了各种各样的诊断方法，这些故障诊断方法可以归为模型类、数据处理类和知识类[2]。其中由于气路系统的数据具有复杂性和强耦合性等特点限制了模型类故障诊断方法的使用。基于数据处理类的故障方法包含文献[3]运用的ANN(Artificial Neural Network)算法[3]和SVM(Support Vector Machine)算法的故障诊断方法、基于RBF(Radial basis function network)算法的故障诊断方法和文献[5]基于DBN(Deep Belief Network,DBN)算法的故障诊断方法等。数据类的故障诊断方法主要对表征系统运行状态的监测数据进行处理，并提取其特征进行故障诊断，符合当下的实际诊断情况。基于知识类的故障诊断算法包含基于信息融合的故障诊断方法[6]和基于故障树的故障诊断方法[7]等，这类方法相对于数据处理类方法整体复杂度偏高。

基于数据处理的故障诊断方法中的基于BP神经网络的故障诊断方法、基于RBF神经网络的故障诊断方法和基于SVM的故障诊断方法[8-9]等本质上属于浅层的神经网络，存在数据泛化性差、诊断精度低和误诊率高等问题[10]。为此本文提出了一种基于主元分析与深度学习相结合的航空发动机气路系统故障诊断方法，其中主元分析方法[11-13]能够有效降低深度学习神经网络诊断模型的复杂度，而DBN神经网络不仅学习能力强，而且具有很强的数据特征提取和特征转换能力。该种方法具有抗干扰性能力强、诊断准确度高和不易漏诊等优点。

1 基本原理

1.1 主元分析原理

主元分析法(Principal Component Analysis，PCA)可以将多个气路系统参数变量转化为少数几个独立的主元变量，从而降低参数的复杂度。主元分析方法能够消除参数数据中的干扰和冗余，在保证准确性的前提下对过量参数数据进行有效降维。

基于主元分析法的数据降维原理及实施步骤如下。

(1)假设存在n组由m个参数组成的样本数据矩阵X为

(1)

对矩阵X进行标准化：

(2)

式中：

(3)

(4)

(2)计算标准化矩阵X′的协方差矩阵Z

(5)

(3) 对协方差矩阵Z进行特征值和特征向量求解

|λI-Z|=0m×1

(6)

特征值需要按由大到小的顺序进行排列，记为：λ1,λ2,…,λm，其对应的特征向量记为：p1,p2,…,pm。

(4)主元贡献率和累计贡献率为

(7)

(8)

在实际应用中通常选取贡献率为85%，表示所获得的主元个数已经包含了原始数据的大部分信息，此时的主元个数即为选取的主元个数。

2.1 深度学习神经网路原理

一个完整的深度信念网络由若干个受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)[14-17]组成，RBM的典型拓扑结构如图1所示。该网络结构包括显层和隐层2个部分。

图1 RBM结构图

假设RBM的显层输入向量为ν，隐层输出向量为h，权值向量为ω，显层偏置向量为a，隐层偏置向量为b。对隐层和显层各单元参数定义如下。

(9)

DBN诊断模型建立步骤如下：

(1)能量函数

当网络处于稳态时能量函数处于最低值。显层输入向量ν与隐层输出向量h之间的能量函数为

(10)

(2)条件概率分布

显层输入向量ν与隐层输出向量h之间的联合概率为

(11)

显层输入向量ν和隐层输出向量h的概率分布为

(12)

(13)

(14)

(15)

(3)能量函数求解

如果要使网络模型达到稳定，则网络能量函数E(ν,h)的值最小。

(16)

由式(9)可知，如果使得能量函数E(ν,h)的值最小，则g(ν)的函数值就最小，即P(ν)的函数值最大。记RBM的参数为θ={a,b,ω}。则P(ν|θ)的偏导：

(17)

将式(10)中的能量函数E(ν,h)带入上式可得

(18)

(19)

(20)

偏导等式的左边是数据样本的期望值，右边的被减数是模型产生样本数据的期望值。

2 基于PCA与DBN的故障诊断方案

基于PCA与DBN的航空发动机气路系统故障诊断模型包含PCA降维模型和DBN诊断模型，首先通过PCA模型对气路系统相关参数数据进行降维，然后将降维后的最优特征参数给DBN模型进行建模和测试。故障诊断方案如图2所示。

基于PCA与DBN的航空发动机气路系统故障诊断具体步骤如下。

步骤1： 利用数据采集网络感知气路系统原始参数数据，将原始数据分为建模样本数据集和测试样本数据集。用建模样本集中的正常样本数据构建PCA建模数据矩阵X；

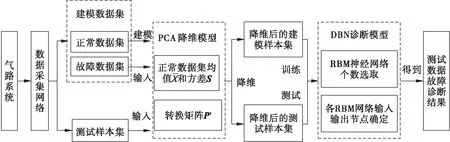
图2 基于PCA与DBN的航空发动机气路系统故障诊断流程

步骤3： 计算得到标准化数据矩阵X′的协方差矩阵Z，并求取协方差数据矩阵Z的特征值λ和特征向量P，根据特征值λ计算得到主元的累计贡献率，合理选累计贡献率阈值，将主元对应的特征向量组成转换矩阵P′，用转换矩阵P′处理标准化的气路系统建模样本集，得到降维后的建模样本集交由合适数量的RBM神经网络组成的l个输入节点和4个输出节点的DBN模型进行建模训练得到建模完成的DBN诊断模型，并将得到的转换矩阵P′进行存储；

步骤5： 降维后的测试样本集交由已经训练完成的DBN诊断模型，输出得到测试样本集的诊断结果，并对其结果进行分析。

3 基于PCA与DBN的诊断试验验证

采用某型航空发动机气路系统试验平台进行试验。根据气路系统的结构和工作机理，选取能够较好反应气路系统运行状态的14个参数：相对物理转速、高压导叶实际值、发动机进口温度、发动机进口压力、压气机出口压力、25截面压气机进口温度、低压转子相对物理转速、主燃油流量给定值、风扇导叶反馈值、喷口喉道面积反馈值、低压涡轮后温度、低压涡轮后压力、大气压力和风扇导叶反馈值作为模型参与诊断的参数。气路系统运行状态可表示为集合{A1,A2,A3,A4}，其中，A1表示气路系统正常；A2表示压气机故障；A3表示低压涡轮故障；A4表示风扇故障。实验中选取气路系统在每种运行状态下的参数数据各100组，其中前75组(共300组)作为训练数据集，后25组(共100组)作为测试数据集。将建模数据集中的100组正常数据集输入到PCA模型，得到协方差矩阵的特征值、均值和方差。各主元贡献率和累计贡献率如表1所示。

表1 主元贡献率及累计贡献率 (%)

为了提高降维结果的科学性和准确性，本文依据累计贡献率的选取范围经验，并结合实际模型选取累计贡献率为90%。通过表2可以看出累计贡献率达到了90%的主元个数为9，表明用9个彼此不相关的主元表示原始的14个参数信息。因此，转换矩阵P′由前9个特征向量组成，其结果如式(21)所示。

P′=

(21)

本文以实际诊断模型诊断的效果为依据，选取3层RBM神经网络建立DBN神经网络诊断模型，第1层RBM神经网络的输入节点个数是9，输出节点是8；第2层RBM神经网络的输入节点数是8，输出节点数是6；第3层RBM神经网络的输入节点数是6，输出节点数是4。

将降维后的建模数据和标签输入给DBN神经网络模型进行建模训练，得到训练优化完毕的DBN神经网络模型。用转换矩阵P′处理标准化后的测试样本数据集，将测试数据输入给训练完成的DBN神经网络模型，得到输出结果如下表2所示。

表2 PCA-DBN故障诊断结果

通过表2可以看出基于主元分析与深度信念网络的故障诊断模型诊断准确率为100%。PCA与DBN诊断模型和DBN诊断模型对气路系统不同典型故障诊断准确率如表3所示。

表3 PCA-DBN模型与DBN模型诊断准确率对比 (%)

通过表3可以看出，DBN诊断模型的故障诊断准确率约为80%，主元分析与深度信念网络诊断模型的诊断准确率远远大于单独的深度信念网络诊断模型。因此，经过主元分析降维后的深度信念网络模型诊断结果比未经过主元分析降维后的深度信念网络模型诊断结果准确率更高。

4 结论

本文使用主元分析数据降维模型，并结合深度信念网络对航空发动机气路系统典型故障进行诊断。通过以上试验可见，将主元分析法与深度信念网络结合的方法能够在一定程度上提高深度信念网络的故障诊断准确率，该方法在航空发动机气路系统系统故障诊断领域具有更广阔的发展前景。