基于OFDM的探地雷达压缩感知成像方法
孙延鹏,张瀚文,屈乐乐,王尔申
(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
探地雷达(Ground Penetrating Radar,GPR)作为一种无损检测设备,已经被广泛应用于基础设施非破坏性评估系统中[1]。雷达系统有两种常见的类型,分别是脉冲雷达和连续波(CW)雷达[2]。
脉冲雷达通过发送和接收窄脉冲信号进行目标成像。窄脉冲信号占用较宽的频率带宽,为了捕获响应信号,需要高速A/D转换器,这导致设计成本较高[3]。CW雷达作为替代脉冲雷达的方案,步进频率是CW雷达中最常见的一种类型。SFCW系统不是发射脉冲信号,而是依次发送以固定的频率间隔逐渐上升的工作频率信号,然后测量每个工作频率对应的幅度和相位响应得到频域响应矩阵,执行逆傅里叶变换进而得到目标特征的时域脉冲响应。SFCW雷达系统不需要高速ADC进行数据采集,能有效降低成本。另外,在每个频率上,SFCW雷达系统以窄带模式工作,这样每个频率信号发射功率更高,从而具有更好的感测性能。但是,SFCW雷达系统最大的缺陷是每个频率信号必须顺序地产生发送和接收,需要较长的时间来完成全频谱扫描。如果被测物体和雷达之间相对位置快速移动,很可能扫描速度不能很好地跟上物体状态变化。
CW雷达的功能测试通常使用SFCW技术。为了产生不同的测试频率,通常使用锁相环(PLL)电路。由于PLL切换频率所需的时间相对较长,因此功能测试面临着感测速度慢的缺点。对此缺陷,目前通常采用同时产生多个测试频率来实现改进,例如利用多个PLL。然而,这种方法具有较高的设计成本和复杂性的缺点[7]。任意波形发生器(AWG)是一种替代测试信号生成方法,可以将其编程为产生包含各种所需频率和相位的信号。然而,AWG设计需要非常高的频率电路和大量用于数据模式存储的存储器,其设计成本也很高。
本文提出了一种新的技术组合OFDM和压缩感测来提高CW雷达测试效率。在这样一个系统中,采用OFDM扩频技术进行多载波信号发送和接收,提高了传输效率。通过使不同频率载波彼此正交能够最小化码间串扰,确保信号的完整性。由于合成的脉冲信号在时域具有稀疏性,因此,压缩感知(CS)技术能够适用于OFDM雷达系统中,通过OFDM技术和CS技术的结合,可以有效提高雷达系统的感测效率。
1 正交频分复用和压缩感知理论
1.1 正交频分复用(OFDM)理论
正交频分复用技术由多载波技术MCM(Multi-Carrier Modulation,多载波调制)发展而来,OFDM既属于调制技术又属于复用技术。OFDM本质上是一个频分复用(FDM)系统,FDM系统是将整个系统的频带划分为多个带宽相互隔离的子载波,虽然通过保护带宽隔离不同的子载波可以避免不同载波的互相干扰,但是牺牲了频谱利用效率。OFDM虽然也是FDM的一种,但它克服了传统FDM频谱利用率低的缺点。
OFDM的基本原理是将信号分割为N个子信号,然后用N个子信号分别调制N个互相正交的子载波。由于子载波的正交性消除了码间串扰,可以有效抵抗频率选择性衰落。子载波的频谱相互重叠,因而可以得到较高的频谱效率。
傅立叶逆变换(IDFT)是用于多载波OFDM信号生成的有效方法[4]。为了产生N个频率音调,使用N个编码数据(k=0,1,…,N-1)作为定义信号频谱的IDFT输入。利用采样频率Fs和采样时间t=nTs,IDFT可以表示为
(1)
其中x(nTs)是时域采样数据点,Fa是两个相邻载波之间的频率间隔。当采样频率Fs等于频率间隔Fa的N倍,即
(2)

Xk编码基于所选择的数字调制方案。数字调制方案有两种主要类型:M相移键控(M-PSK)和M相正交幅度调制(M-QAM)。在这种设计中,利用正交相移键控(QPSK)使Xk信号幅度相同,而它们的相位被随机化。这样编码在逆傅里叶变换后生成的OFDM时域信号能产生更高的幅度和更高的信噪比(SNR),产生更高的测试精度[8]。

图1 N载波OFDM信号频域
在探地雷达系统中,目前应用最多的是步进频率体制的。在步进频率探地雷达系统中雷达信号的工作频率以固定的频率间隔逐渐上升,将OFDM技术应用于探地雷达系统中,可以将不同工作频率的信号同时传输,一次传输整个频带的信息,能够有效提高系统速度。
1.2 压缩感知理论
压缩感知(Compressive Sensing,Compressed Sensing,or Compressed Sampling,简称CS)是一种寻找欠定线性系统的稀疏解的技术。相较于奈奎斯特理论,这种方法利用信号的稀疏性从较少的观测值还原出原信号。其中CS三要素主要包括信号的稀疏变换、非相关测量及重构算法[6]。
设信号x∈CN是一个有限长的离散时间信号,在某个基矩阵ΨN×N上稀疏度为K,其中K≪N。可用正交变换矩阵表示为
x=Ψθ
(3)
其中Ψ是稀疏变换矩阵,θ是具有K个非零元
素的N×1的向量。根据CS理论,如果信号x在稀疏变换矩阵Ψ上是稀疏的,则将x投影到低纬空间,得到的测量值可用矩阵表示为
yM×1=ΦM×NXN×1=ΦM×NΨN×NθN×1
(4)
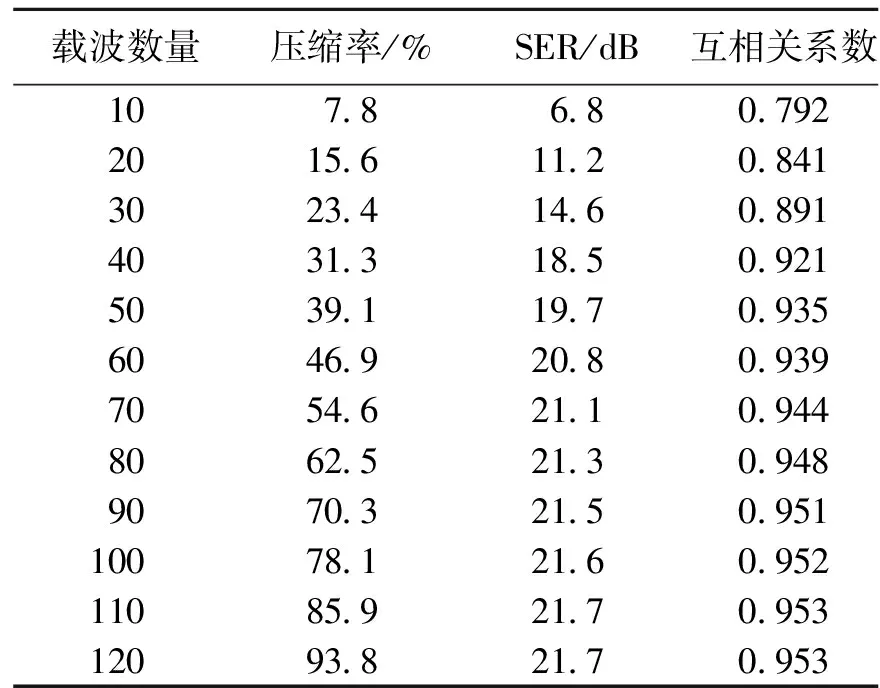
其中Φ表示M×N的测量矩阵,M(K θ=argmin‖θ‖1,s.t.y=ΦΨθ (5) 为了满足RIP准则,必须使稀疏基和测量矩阵具有不相干性[6]。而CS相关研究[12]表明随机矩阵能以很大概率与稀疏基不相干。因此可以选择随机矩阵作为测量矩阵。 在OFDM雷达系统设计中,CS算法将确定要传输的M个频率,并且进而减少整体操作时间和功耗。使用CS传输少量频率,可降低测试信号功耗和测试信号复杂度,同时保持测试覆盖率和性能水平。 在GPR应用场景中目标空间通常较稀疏,所以可以随机选取M个载波用于SFCW雷达测量中。同样的,利用随机选择的M个载波进行OFDM信号的生成和传输能够有效降低测试信号的功耗和测试信号的复杂性。 OFDM-CS探地雷达系统整体流程如图2所示。 图2 OFDM-CS探地雷达系统框图 (2) 对OFDM码元信号进行频率压缩,选择适当的压缩算法,在N组调制后的载波信号中选择部分载波进行压缩。 (3)采用傅里叶逆变换可以快速实现子载波叠加的过程,因此将压缩后的多载波信号经过快速傅里叶逆变换(IFFT)得到压缩后的时域OFDM信号。 (4) D/A转换并根据实际情况选择是否上变频后在天线中发射。 (5) 接收天线接收到来自目标的回波信号。 (6) A/D转换并根据实际情况选择是否下变频。 (7) 采样后的信号通过快速傅里叶变换(FFT)算法得到接收端的OFDM信号的频率响应。 (8) CS重建,即通过分析发送和接收端的OFDM信号,计算目标的增益和相位频率响应,得到压缩的响应数据矩阵并进行CS重建以恢复频谱的时域响应。 (9) 最后根据恢复出的频谱时域响应恢复出雷达图像。 为了设计OFDM系统,应考虑几个基本参数:OFDM信号B的带宽、子载波数N和循环前缀Ng的长度。参数的选择很大程度上取决于OFDM系统正在运行的信道条件。通常使用两个参数来表征通道:延迟扩展τ和最大多普勒扩展fd。延迟扩展描述了来自信道视距及信道多径分量之间的时间差。当循环前缀持续时间短于延迟扩展时,多径分量引起符号间干扰(ISI)。最大多普勒扩展与通道被认为与遭受时间不变衰落的信道相干时间成反比。 在OFDM体制的GPR系统中,距离分辨率Δt取决于发射信号的带宽。关系可表示为 (6) 公式6表示信号带宽由所需分辨率决定。信号带宽由于硬件和传播许可限制而不能任意增加,因此对范围分辨率有一定的约束。 有用的符号时间Tu=NT应该比通道相干时间短得多。如果我们将多普勒扩展fd的倒数作为相干时间的度量,则有用符号时间Tu应满足 (7) 而对于GPR,因为探地雷达设备通常移动很慢,多普勒扩展几乎可以忽略,因此,一般情况下都能满足公式(7)的约束条件。 N的选择主要影响目标轮廓估计精度,因此N必须足够大以使得每个子载波经历平坦的衰落信道。 在OFDM-CS探地雷达系统中,利用OFDM正交特性同时处理多个单独的频率,将指定的带宽分成子带而不是每个频率顺序地步进,是一次传送整个频带。CS利用发射信号和测试环境的稀疏性在N组正交载波中选择了M组载波,减少了雷达系统传输的频率数量,这有利于减少频谱扫描时间,进而减少整体操作时间和功耗而不会丢失任何重要信息。使用CS传输较少数量的频率可降低测试信号功耗和测试信号复杂度,同时保持测试覆盖率和性能水平。 对于SFCW探地雷达系统,雷达的工作频率以固定的频率逐渐上升,而不同频率的雷达信号必须在锁相环中顺序生成,在带宽较大的雷达系统中,采用SFCW系统进行感测耗时较长。为降低设计成本并提高雷达系统感测速度,在本文提出的将OFDM和CS算法相结合的方式中,OFDM可以同时生成整个频带的数据,CS算法减少了需要采样的频点数量,提高了雷达系统的发射和采样速度。为了展现OFDM-CS系统和SFCW系统的性能等效性,在MATLAB中分别用两种方式进行了探地雷达仿真实验。 仿真实验环境如图3所示,在高斯白噪声环境下进行,信噪比为20 dB。两个目标点的位置分别为(10,40)和(30,40)(单位:cm)。雷达收发天线以1 cm步长在方位向移动,共有30个测量位置。在该仿真环境下,分别采用SFCW和OFDM-CS的方法测量目标位置信息。 图3 探地雷达系统仿真实验探测模型 对于SFCW雷达系统,发射电磁波信号的起始频率为f0=1 GHz,截至频率FH=3 GHz,频率步进点数N=128。同样的,OFDM-CS雷达系统频点数和SFCW雷达系统相同,采用128个QPSK调制的正交载波,起始频率和截止频率也与SFCW-GPR系统相同。 成像区域沿方位向从1 cm到40 cm,沿距离向从30 cm到50 cm,被均匀划分为个大小为1的网格。对该实验场景,分别用SFCW方法和OFDM-CS方法生成B-scan图像如图4、5所示。其中图5是用30个频点数据恢复生成的B-scan图像。 图4 SFCW B-scan图像 图5 OFDM-CS B-scan图像 对比图4、图5,可以发现采用SFCW方法和OFDM-CS方法成像都恢复出了目标信息。为了测量图像相似度,计算两张图片的二维互相关系数为0.891,以SFCW图像作为参考计算OFDM-CS图像SER为14.61 dB。 在其他压缩比下重复OFDM-CS的B-scan实验,对互相关系数和SER进行定量分析,分析结果记录在表1中,压缩率与互相关系数和SER的相关关系如图6、7所示。从图6可以看出,随着压缩率的提高互相关系数逐渐提升。从图7可以看出,随着压缩率的提高SER逐渐提升。两种方法的压缩率与互相关系数呈正相关,压缩率与SER呈正相关。分析表1数据,可发现两种方法的成像结果的互相关峰值在0.953,这表明使用OFDM-CS和SFCW方法的测试效果高度相似,都可以有效产生相同的测试结果。对比两种方法的SER,可以发现压缩率在大于46.9%之后SER大于20 dB,这说明两种方法的重建误差很小。 表1 不同压缩率下的SER和互相关系数 图6 不同压缩率的互相关系数 图7 不同压缩率的SER 在该仿真环境下,OFMD-CS雷达系统的整个频段的一次完整发射时间即为OFDM符号周期,T_symbol=NTs=64ns。对于SFCW雷达系统,发射信号频率以频率间隔逐渐上升,而频率切换需要利用锁相环。锁相环从一个频点快速跳变到另一个频点的锁定时间通常为50us, SFCW雷达系统整个频段所需的频率切换时间为6.4ms。对比可直观发现,OFDM-CS雷达系统发射时间远小于SFCW雷达系统,并利用CS算法从较少频点数据可以重构出回波信号,采集时间大大降低,从而提高了系统的成像速度。 本文提出了一种OFDM-CS探地雷达系统成像方法,和SFCW探地雷达系统进行了对比实验,实验结果表明该方法能在有效缩短频点扫描和采集速度的同时达到与SFCW方法相近的成像效果。2 OFDM-CS的探地雷达系统

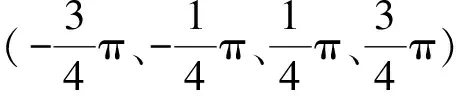
3 仿真实验





4 结论

