超大型冷却塔施工全过程风振响应及风振系数演化规律研究
朱 鹏, 柯世堂
(1.南京航空航天大学 土木工程系,南京 210016;2.中通服咨询设计研究院有限公司,南京 210019)
目前我国在建和拟建的火/核电厂超大型冷却塔高度远超规范[1-2]高度限值(190 m)、突破世界纪录(200 m)[3],此类超大型冷却塔与中小型常规冷却塔相比有两个鲜明特点:表面三维动态风荷载效应更加显著[4-6]、主体结构施工周期更长且难度更大[7-8],整体结构施工进度通常需要12~16个月时间。因此,现有设计中采用成塔单一风振系数与强度控制目标来指导结构抗风并不能真实反应超大型冷却塔施工过程中动态风荷载特性与结构实际受力性能的演化,完全忽略了施工过程中混凝土材料和结构性能的实时演化。因此,探究施工全过程风振机理问题正是目前此类超大型冷却塔抗风研究的关键和瓶颈。
针对大型冷却塔的风振响应与风振系数研究,许林汕等[9]采用虚拟激励法与振型迭加法进行了冷却塔结构的随机风振响应分析,定量地比较了风振响应中背景分量与共振分量的贡献;柯世堂等[10]系统分析了冷却塔结构本身和外界干扰对强风作用下结构风致振动的影响,总结了特征尺寸、阻尼比和周边干扰对冷却塔风振响应的影响规律;柯世堂等[11]通过同步测压和测振冷却塔气弹模型风洞试验,探讨了自激力效应对于大型冷却塔表面风压和风振响应的影响;邹云峰等[12]将我国规范与德国VGB规范[13]等效静力风荷载计算公式进行了对比,探讨了风振系数与平均风压分布系数取值差异对于冷却塔内力及变形分布的影响。然而,已有研究成果鲜有涉及大型冷却塔施工全过程风振响应机理分析,更缺乏超大型冷却塔施工全过程风振系数的精细化取值研究,给此类超大型冷却塔施工期的风荷载取值和抗风安全带来隐患。
鉴于此,以西北地区某在建超大型冷却塔(210 m)为背景,建立不同施工高度冷却塔高精度三维实体模型,采用LES技术进行了冷却塔施工全过程脉动风荷载数值模拟。结合有限元完全瞬态法对比分析超大型冷却塔施工全过程塔顶位移、子午向轴力及环向弯矩等典型响应风振实时变化特性,并基于三种典型目标和五种取值方法系统探讨了超大型冷却塔施工全过程风振系数沿高度和环向角度的演化规律,最终提出了以施工高度为函数的超大型冷却塔施工全过程风振系数计算公式。
1 算例说明
1.1 工程介绍
本工程在建超大型冷却塔塔高210 m,喉部标高157.5 m,进风口标高32.5 m。塔筒采用52对X型支柱支撑并与环板基础连接,X型柱采用矩形截面,截面尺寸为1.2 m×1.8 m,环板基础宽12.0 m,高2.5 m。表1给出了超大型冷却塔结构典型的特征尺寸。

表1 超大型冷却塔结构特征尺寸列表
1.2 施工全过程模型定义
为系统分析施工全过程超大型冷却塔风振响应特性及风振系数演化规律,综合考虑工程施工进度与数值计算精度,按塔筒施工模板层数划分了八个典型施工工况,各工况参数如表2所示。
1.3 计算参数说明
本工程超大型冷却塔所处地貌类别为B类,百年一遇最大风速为23.7 m/s,对应风压为0.35 kN/m2,粗糙度指数取为0.15,成塔结构表面平均风压采用冷却塔规范中实测风压分布曲线作为标准。
2 风荷载数值模拟
2.1 方法介绍
结构抗风研究中流体视为黏性不可压缩,对瞬态的N-S方程进行空间平均,可得大涡模拟方法[14]的控制方程为
(1)

表2 超大型冷却塔施工全过程典型工况参数列表
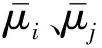
(3)
根据Smagorinsky提出的基于涡旋黏度假设的亚格子模型,引入Boussinesq假设,亚格子应力可表达为
(4)
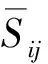
(5)
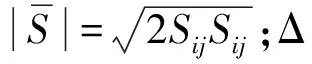
该模型适合工程应用、无需采用试验滤波且计算量少,适用于此类高雷诺数冷却塔的模拟[15]。
2.2 网格划分与参数设置
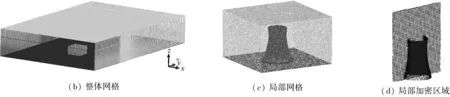
为保证数值计算中超大型冷却塔雷诺数与实际工程中相似,数值计算中按足尺建模。计算模型塔高H=210 m,塔底直径D=180 m,流体计算域长(Y=30D)×宽(X=20D)×高(Z=5D)=6 000 m×4 000 m×1 000 m(Y为顺风向,X为横风向,Z为高度方向),模型阻塞率小于1%,满足规范要求。计算模型中心距离计算域入口10D,为使尾流得到充分发展,出口位置距离模型20D。
为了更好地兼顾计算效率与精度,计算域划分为局部加密区域与外围区域。在冷却塔结构附近的内部区域选用具有良好适应性的非结构化网格单元,同时采用网格控制措施对模型表面网格、模型附近流动变化剧烈区域网格进行加密处理,严格控制近壁面的网格尺度,进而完成整个内部区域的混合网格离散。在远离冷却塔模型的外围空间,选用具有规则拓扑的结构化网格进行离散,从而显著减小计算模型的网格总数提高了计算效率。核心区最小网格尺寸为0.2 m,全塔结构总网格数量控制在1 280万左右。
通过UDF文件定义边界条件,入口边界条件为速度入口(Velocity Inlet),按B类地貌风剖面设置相应参数;出口采用压力出口边界条件(Pressure-Outlet),相对压力选为零;计算域顶部和侧面采用等效于自由滑移壁面的对称边界条件(Symmetry);地面以及建筑物表面采用无滑移壁面边界条件(Wall)。空气风场选用不可压缩流场,亚格子模型采用Dynamic Smagorinsky-Lilly模型,并采用SIMPLEC方法进行离散方程组的求解。LES计算的时间步长取为0.05 s。流体计算域及网格划分如图1所示。
2.3 风场模拟
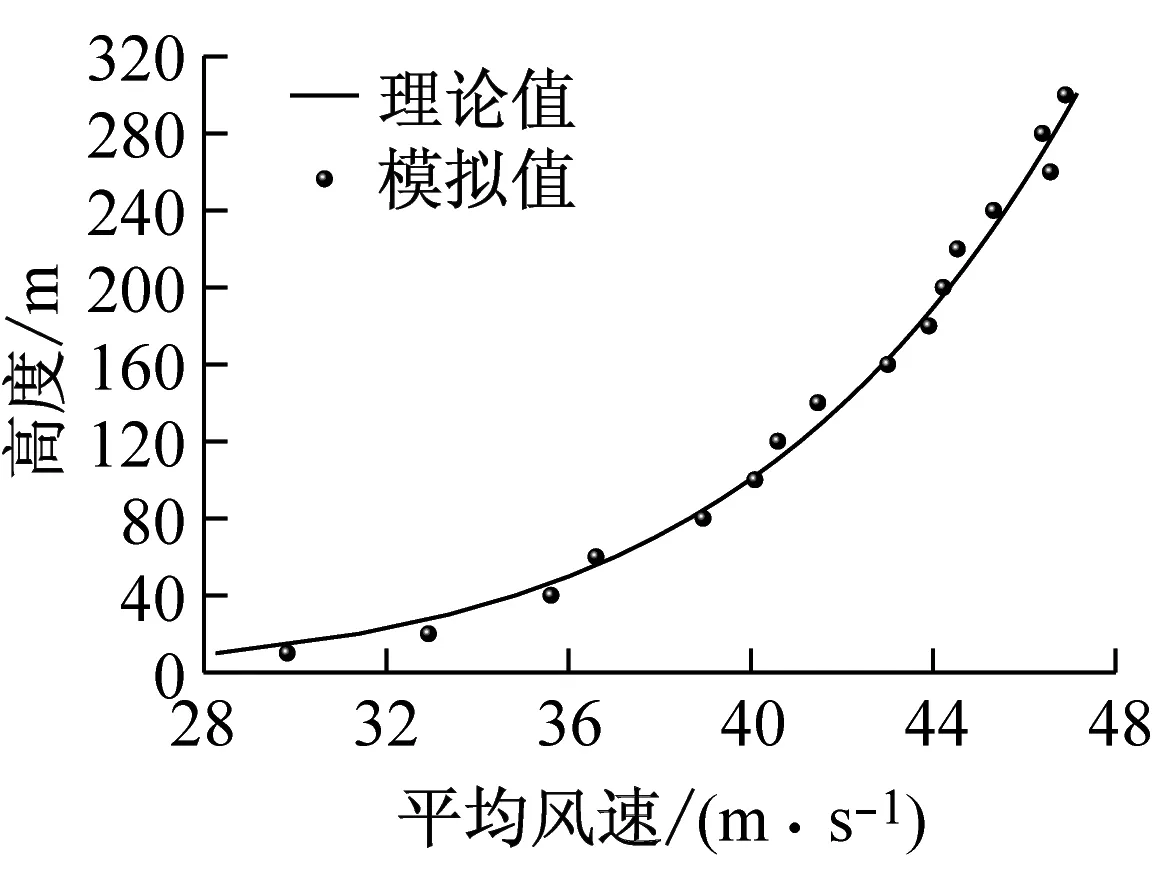
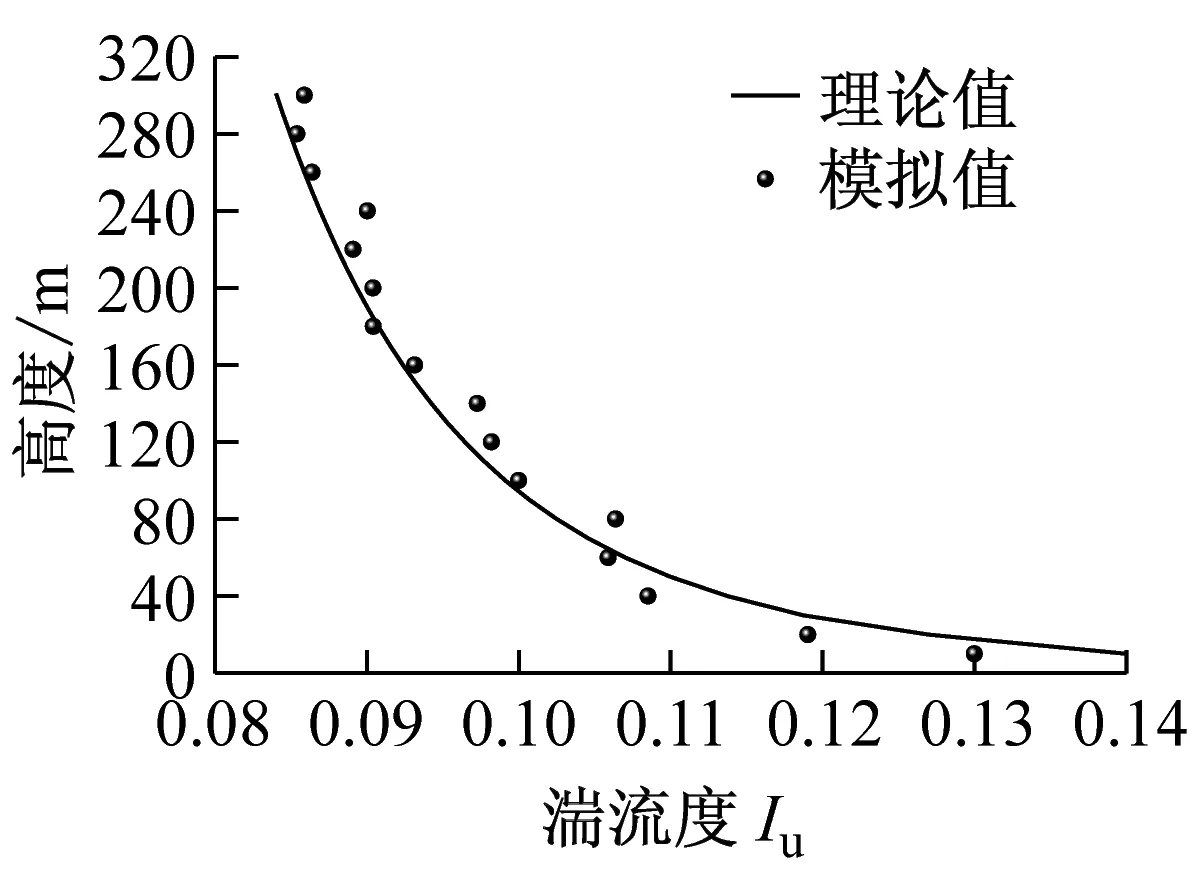
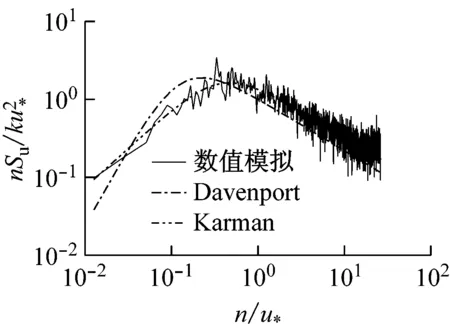
试验风场按《建筑结构荷载规范》中的B类地貌模拟[16],风场模拟的主要指标为平均风速剖面、湍流度剖面和顺风向脉动风谱等,数值模拟结果见图2。可见脉动风场模拟较好,满足规范要求。
2.4 模拟结果及分析
2.4.1 典型测点风压
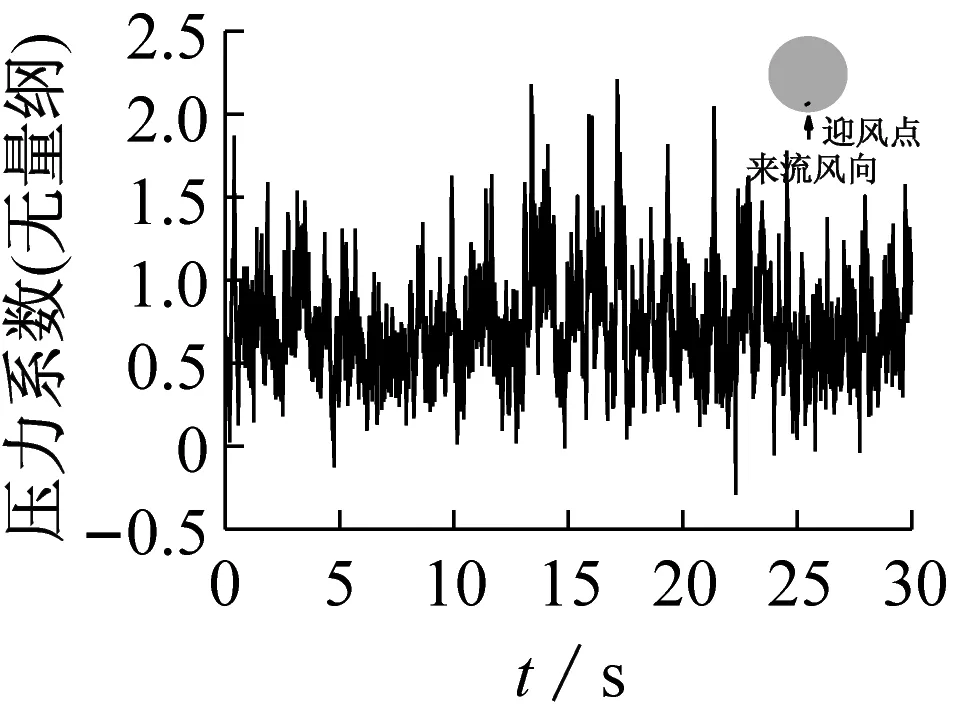
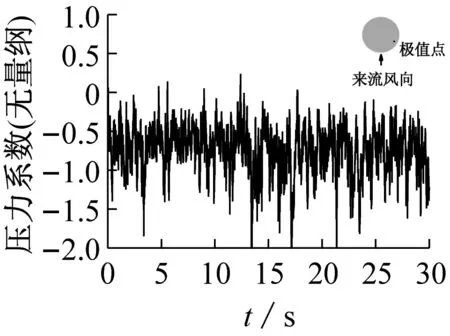
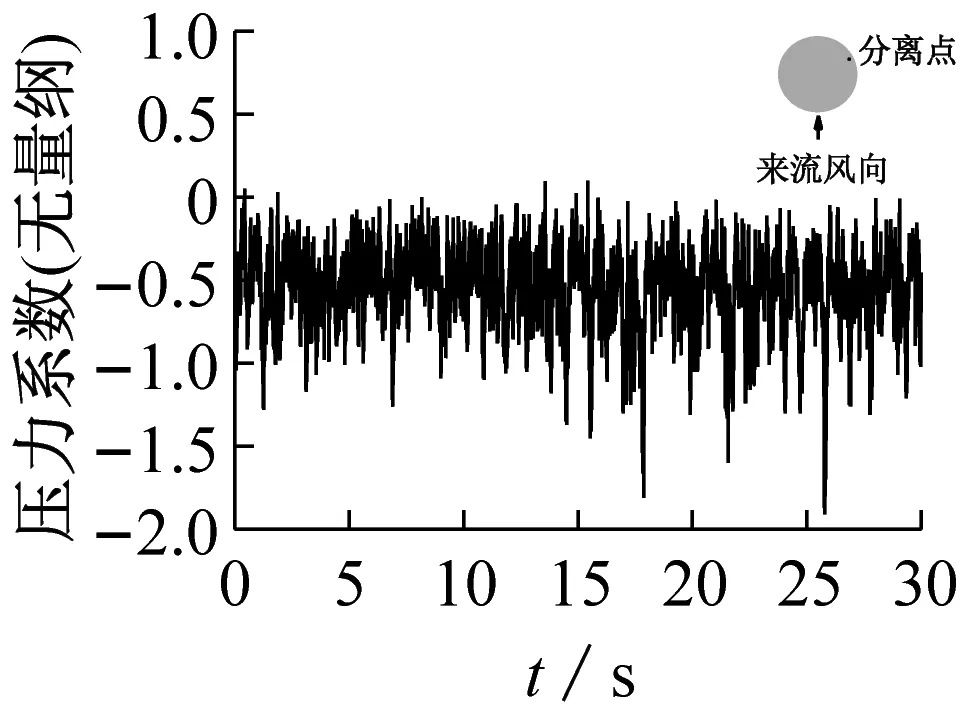
通过LES获得施工全过程冷却塔表面脉动风压时程,受限于篇幅,图3仅给出了成塔工况迎风面、侧风面、分离点及背风面测点的风压系数时程曲线。
图4给出了各测点对应的功率谱密度函数曲线,对比发现不同脉动风荷载功率谱均在低频段出现峰值,脉动风压能量主要集中在低频区域,而位于结构迎风面的测点功率谱数值较分离点与背风面测点谱值稍大。

(a) 计算域参数设置示意图
(a) 平均风速剖面
(b) 湍流度剖面
(c) 脉动风谱
(a) 迎风面测点
(b) 侧风面测点
(c) 分离点测点

(d) 背风面测点
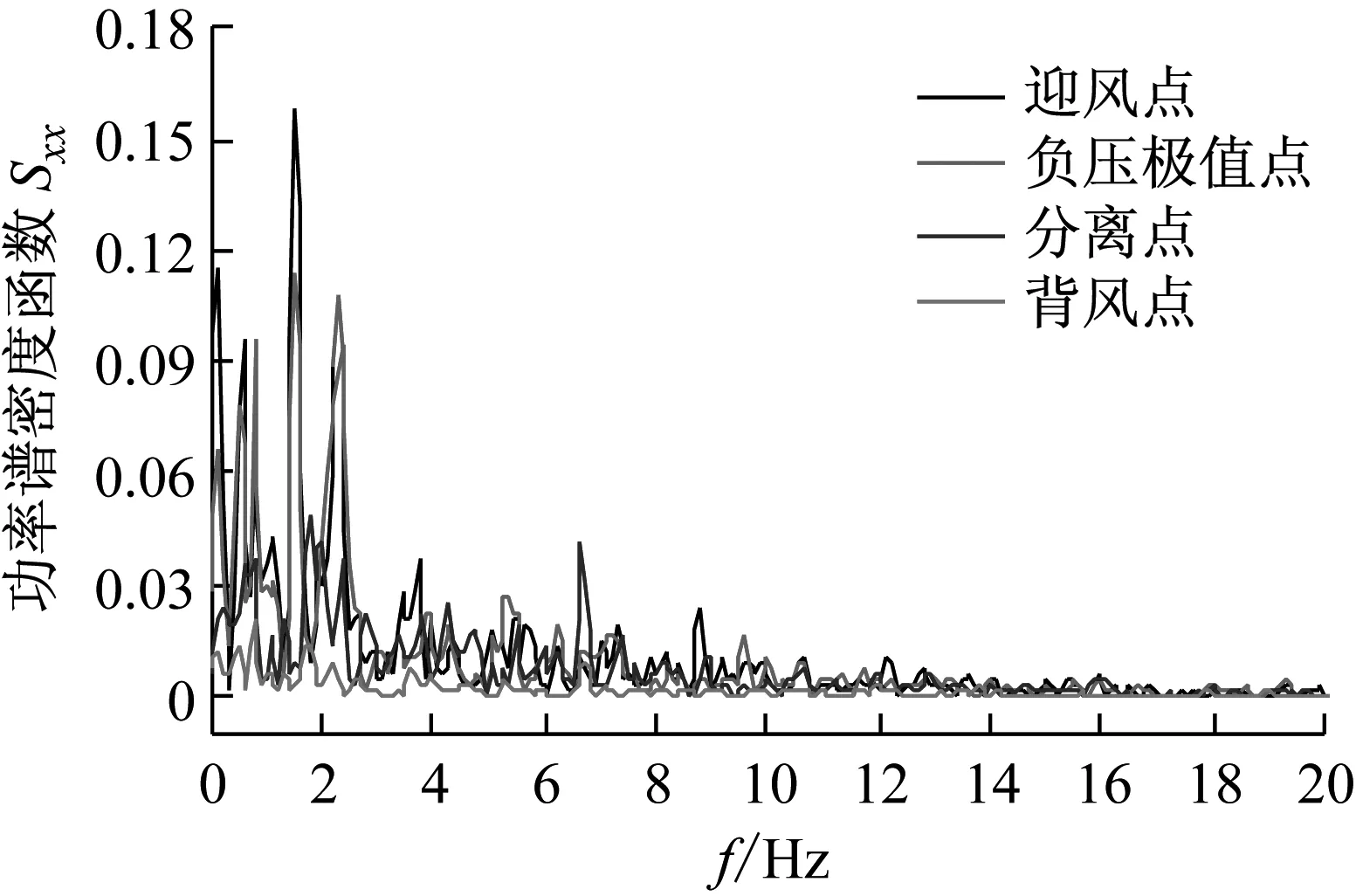
图4 成塔典型测点功率谱密度函数曲线图
2.4.2 平均与脉动风压有效性验证
考虑到冷却塔规范仅给出了冷却塔成塔状态表面平均风压的分布规律,图5(a)给出了成塔典型断面平均和脉动风压与国内外实测及风洞试验分布曲线对比示意图。对比发现数值模拟与风洞试验的平均风压分布曲线吻合很好,在迎风面、负压极值区以及背风面分离点处压力系数数值均与规范曲线接近,验证了基于大涡模拟获得的平均风压的有效性。图5(b)中脉动风压分布曲线与国内实测和风洞试验曲线较为接近,数值上要小于国外实测结果,大于国内现场测试数值,考虑到脉动风压分布与实测塔所处的地形、来流湍流和周边干扰密切相关,且本文大涡模拟获得的脉动风压分布趋势和数值均接近并在已有的实测结果分布范围内。因此本文基于大涡模拟得到的脉动风压具有一定的有效性,可用于后续风振响应时程分析。
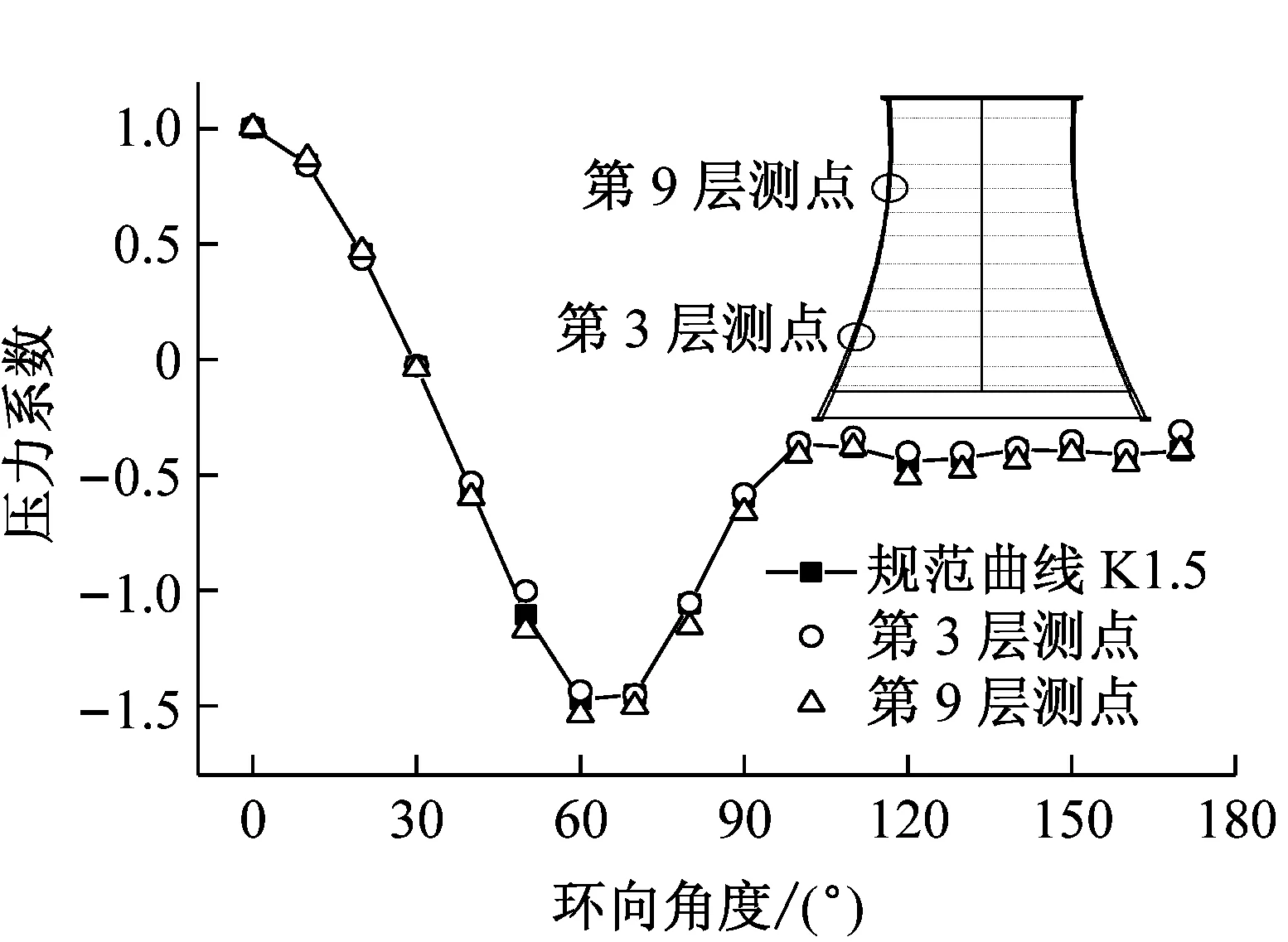
(a) 平均风压
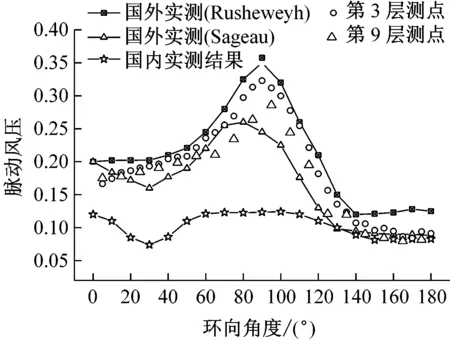
(b) 脉动风压
2.4.3 施工全过程平均风荷载
图6和图7分别给出了超大型冷却塔施工全过程各工况外表面压力系数分布云图及典型断面数值曲线,对比发现:①施工全过程八个典型工况塔筒的压力系数虽数值上差异较大但是分布趋势较为接近,这主要是由于施工高度的增长并未改变圆柱形结构的风场绕流特性,气流在塔筒前沿受撞击分离形成分离泡并在塔筒侧风面逐渐脱落,最终导致塔筒环向仅迎风面为正压带;②施工高度增长显著降低了冷却塔侧风面与背风面的负压值,以成塔工况最为显著。
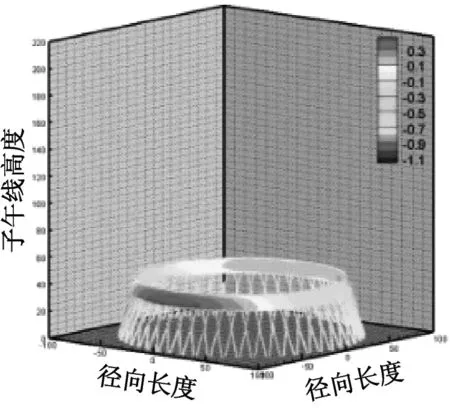
(a) 工况一
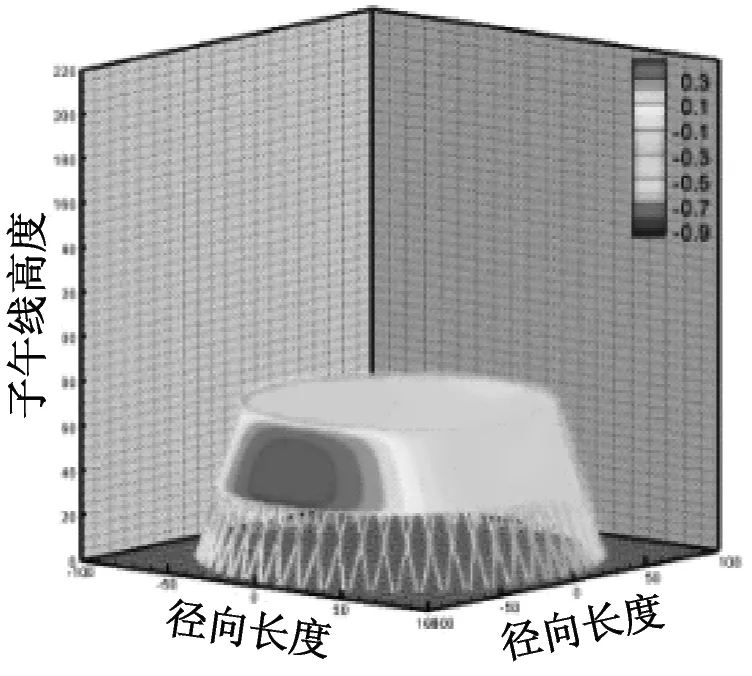
(b) 工况二
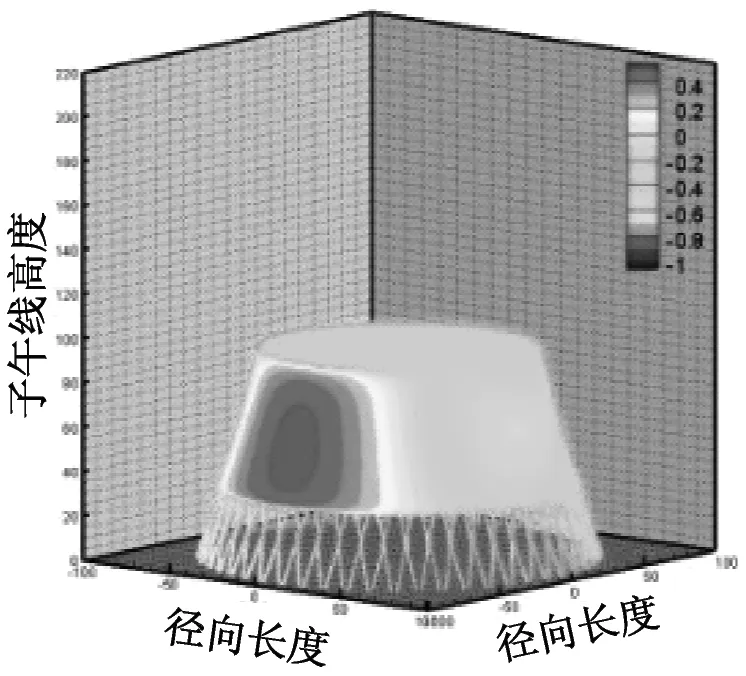
(c) 工况三
(d) 工况四
(e) 工况五

(f) 工况六
(g) 工况七
(h) 工况八
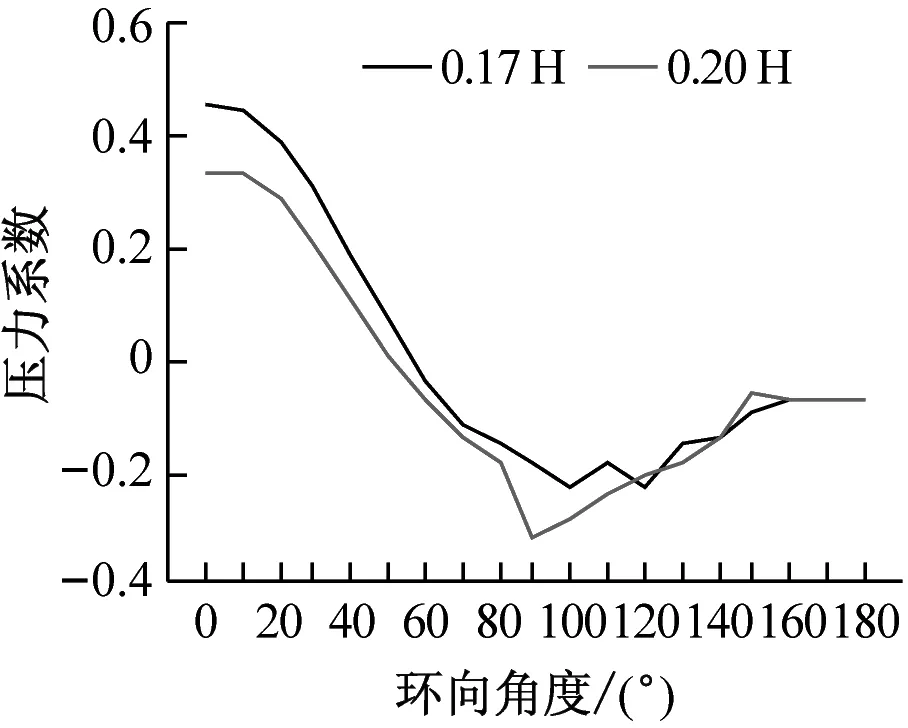
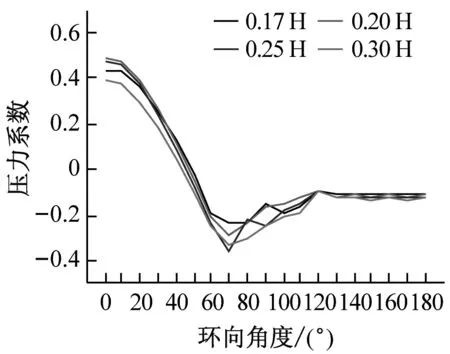
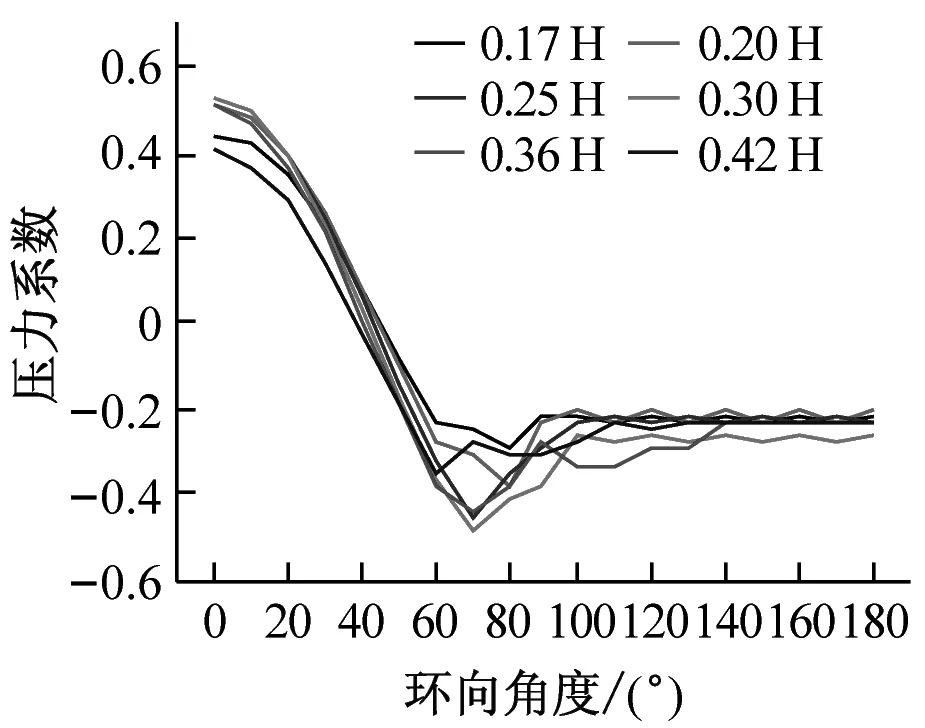
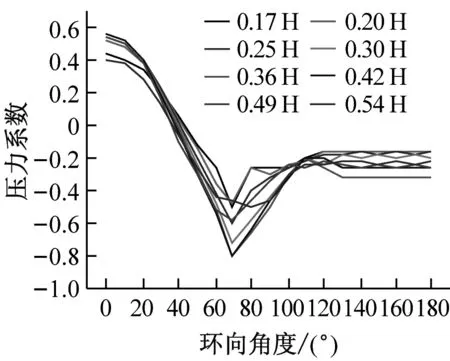
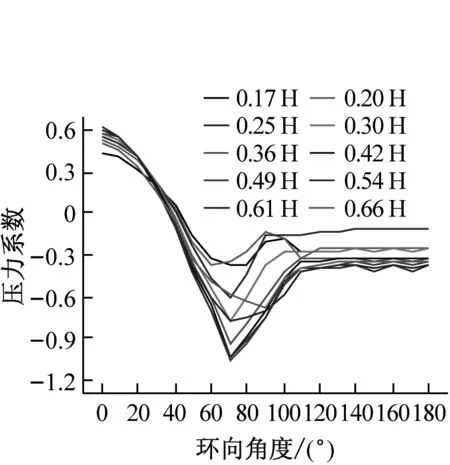
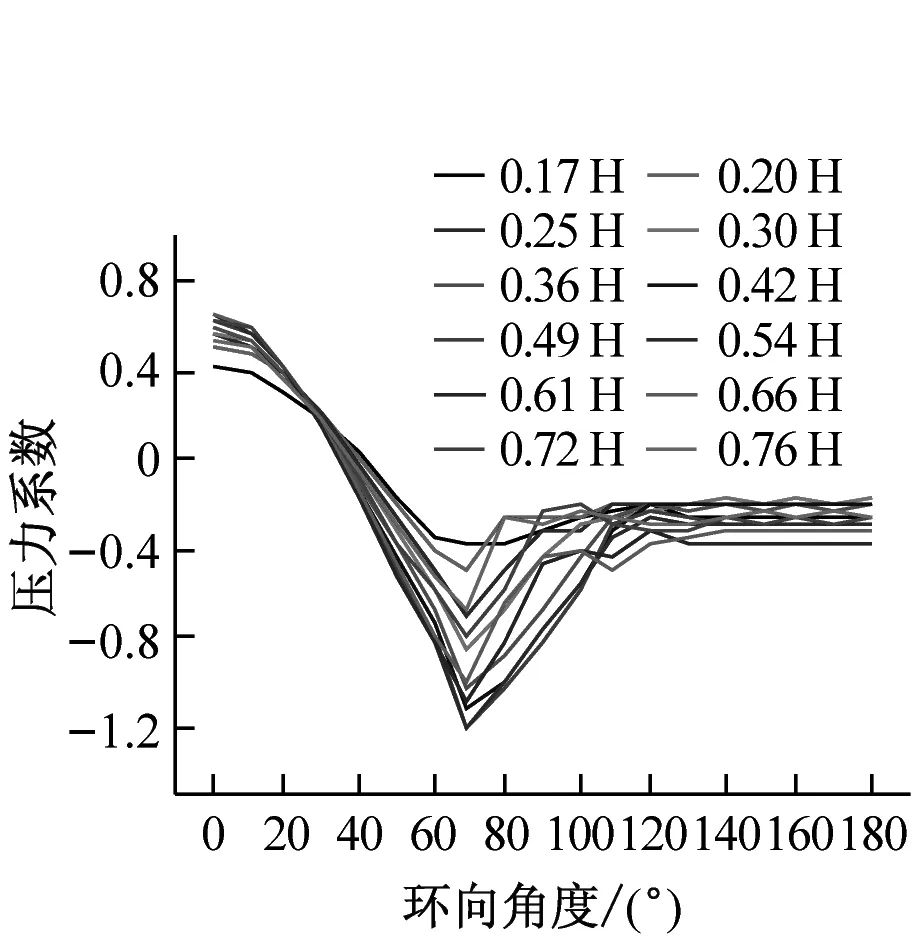
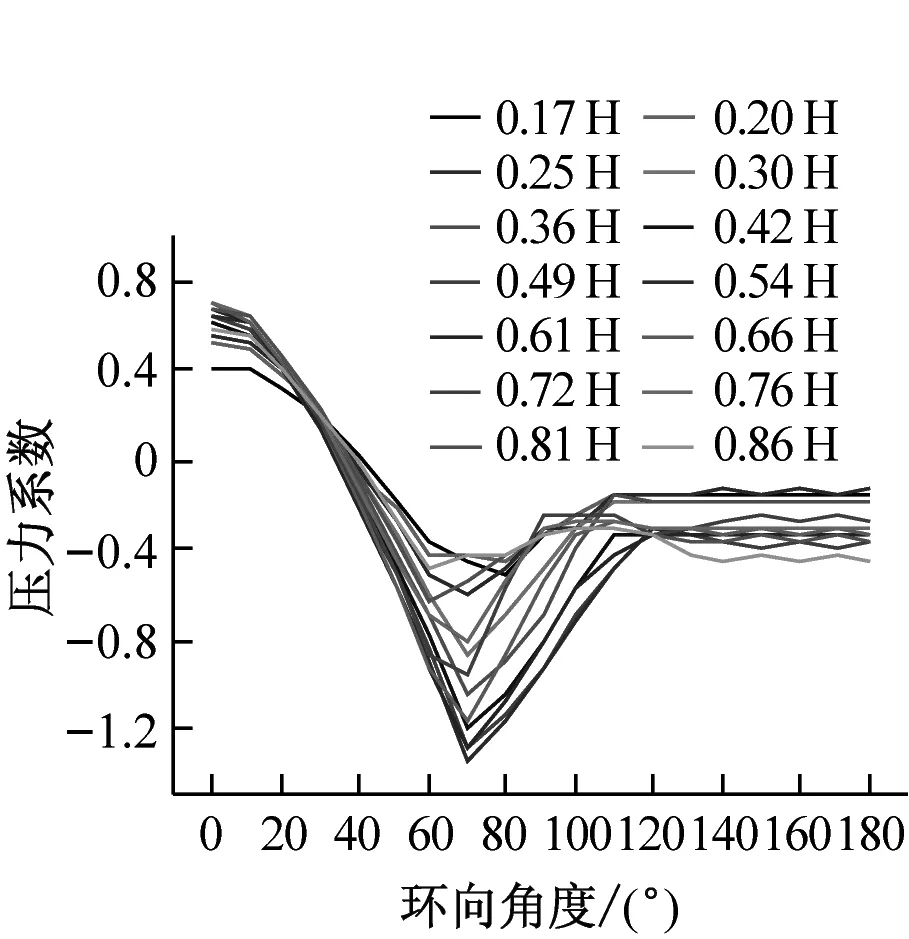
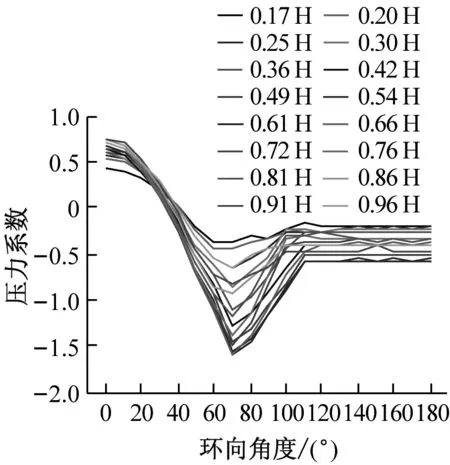
分别选取0°、70°、120°及180°四个典型子午向角度分析冷却塔施工全过程表面压力系数分布,如图8所示。分析得到施工高度的增长对于各典型子午向角度压力系数分布趋势影响较小,迎风面与侧风面子午向风压呈现出显著的凹凸变化,背风面子午向风压均呈现出折叠变化的趋势。此外,施工高度的增长显著增大了压力系数数值分布范围,以成塔工况最为显著。
3 施工全过程风振响应分析
3.1 动力特性演化特性
基于ANSYS有限元分析软件二次开发,采用Shell63壳单元和Beam188梁单元建立超大型冷却塔不同施工阶段有限元模型,采用分块Lanczos方法对八个工况冷却塔模型进行动力特性分析。图9给出了各工况模型前50阶结构自振频率分布曲线,成塔结构基频仅为0.574 Hz,不同施工阶段冷却塔自振频率变化显著,随着施工高度的增长冷却塔基频逐渐降低,且增长趋势变缓。
图10给出了施工全过程不同工况前10阶模态的固有频率随环向谐波数的变化示意图,对比发现各工况冷却塔的最小固有频率均出现在4个环向谐波处,且随着自振频率的增大环向谐波数呈现变多的趋势。
(a) 工况一
(b) 工况二
(c) 工况三
(d) 工况四
(e) 工况五
(f) 工况六
(g) 工况七
(h) 工况八
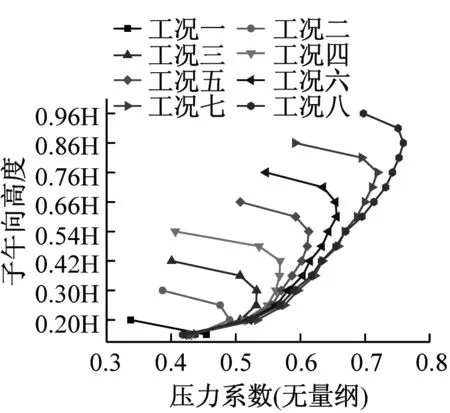
(a) 0°子午向
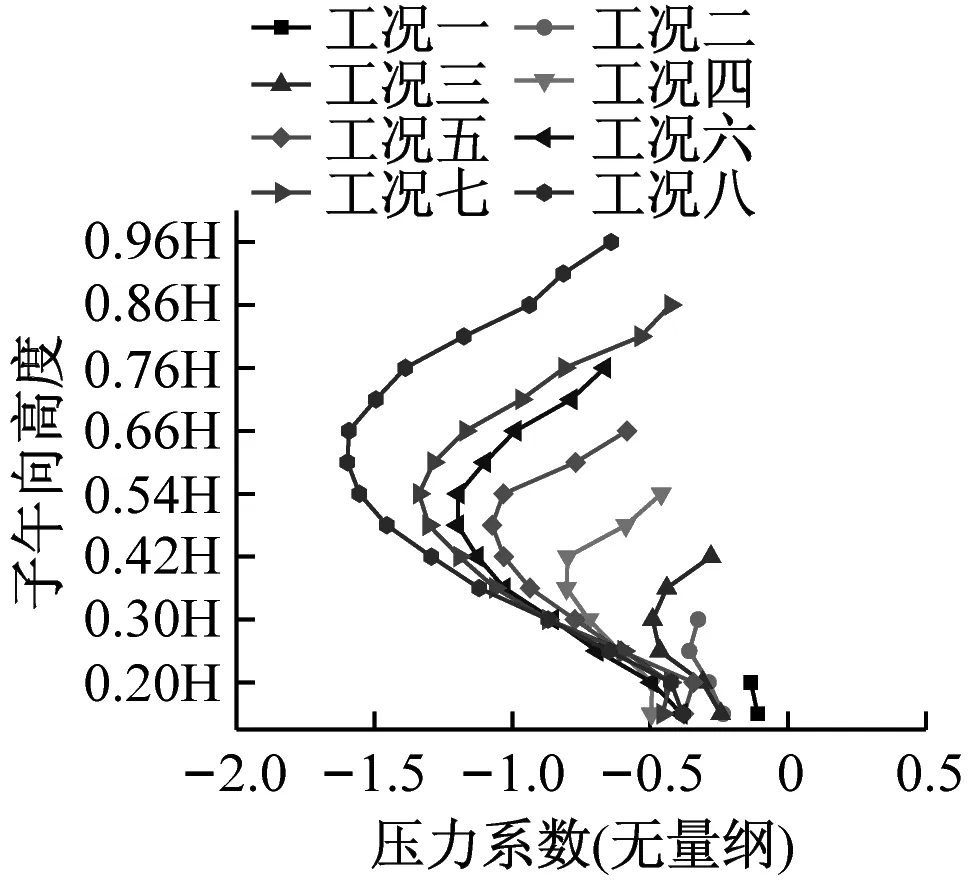
(b) 70°子午向
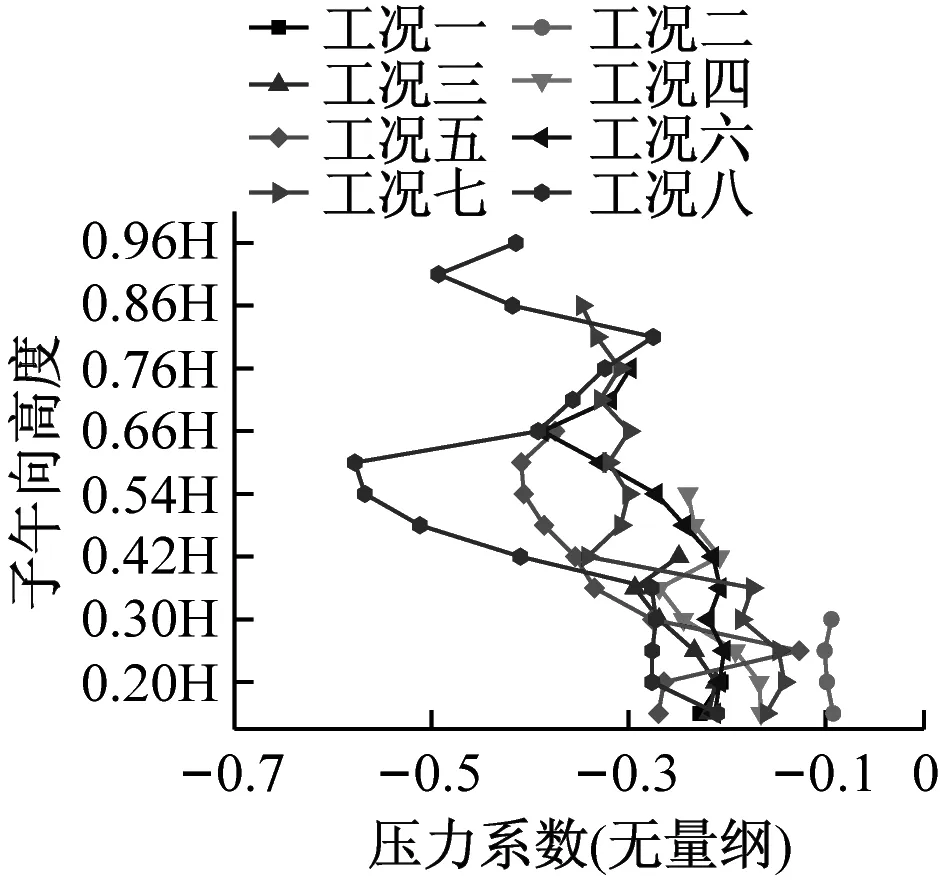
(c) 120°子午向
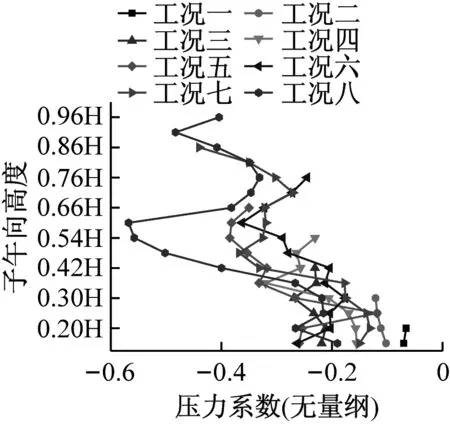
(d) 180°子午向
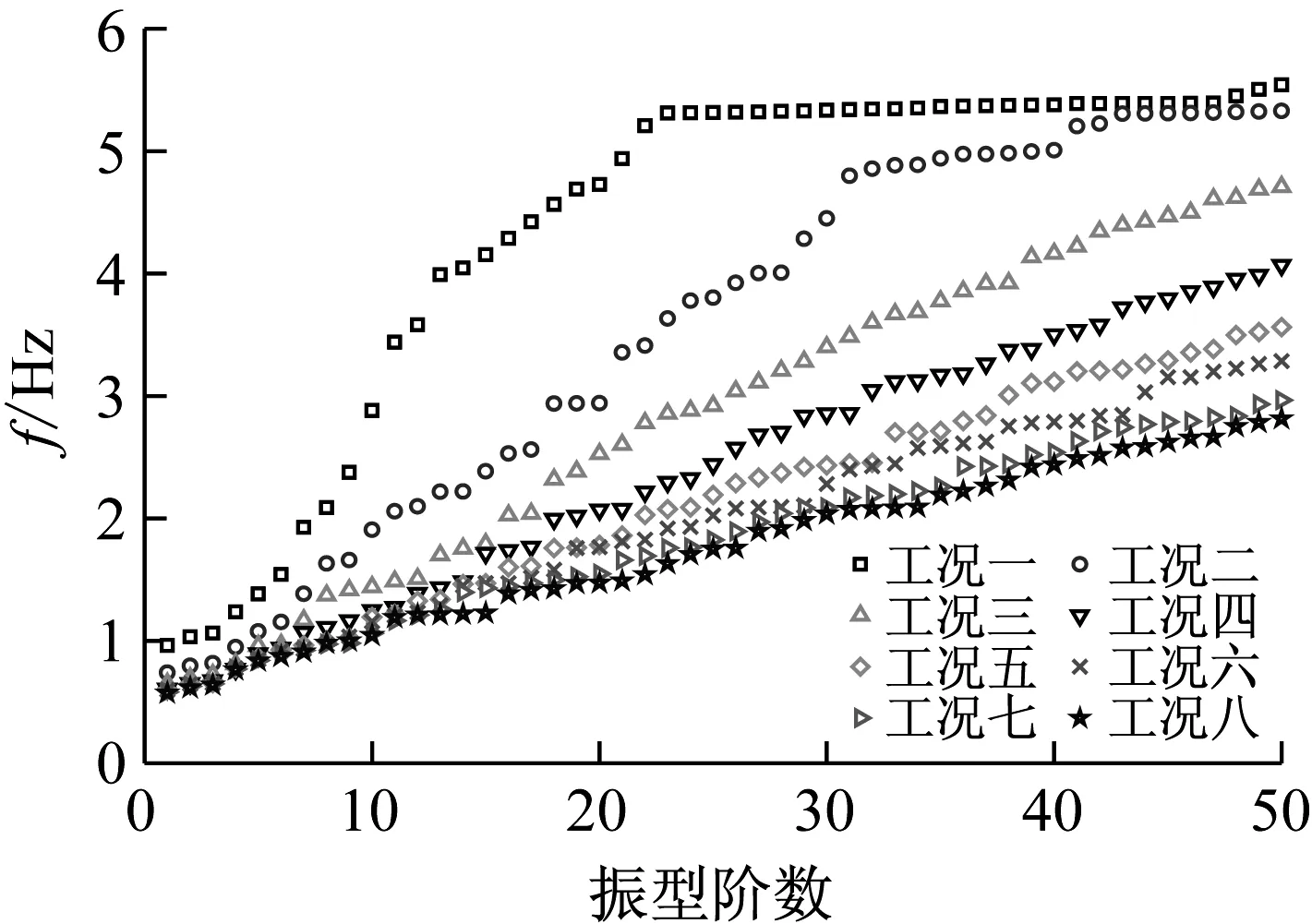
图9 各工况前50阶频率分布曲线示意图
表3给出了超大型冷却塔施工全过程各工况冷却塔倾覆模态列表,对比发现随着施工高度的增长结构倾覆振型所在模态不断向后推移,同时倾覆振型被激发的频率逐渐降低。动力特性分析表明不同施工状态对冷却塔频率分布影响较大,但是对模态振型影响较小。
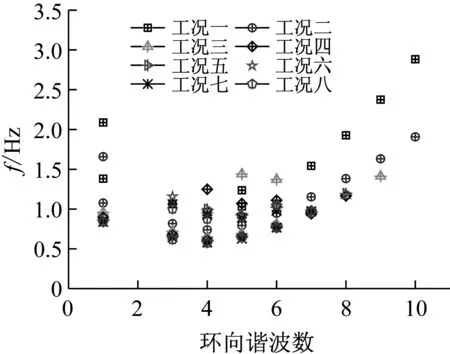
图10 各工况频率随环向谐波数变化示意图

表3 超大型冷却塔施工全过程八个典型工况倾覆模态列表
3.2 施工全过程风振响应分析
冷却塔结构在脉动风作用下的动力平衡方程为
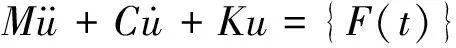
(6)
采用ANSYS中完全瞬态动力方程求解实现对冷却塔风振响应的时程分析,接合APDL语言将脉动风压时程曲线导入ANSYS并施加于不同施工高度工况,采用Newmark-β法求解式(6)。进而通过后处理获得脉动风作用下冷却塔施工全过程冷却塔所有部位内力与位移响应时程。
3.2.1 塔顶位移风振响应
图11给出了超大型冷却塔施工全过程各工况塔顶迎风面节点位移响应功率谱。对比分析得到各工况冷却塔结构的背景响应与共振响应在频谱上分离显著,并且由于冷却塔表面气动力荷载输入的能量主要集中在0~0.5 Hz,不同施工阶段背景响应与共振响应所占比例是不同的;随着施工高度的增长塔顶位移功率谱峰值呈现出先增大后减小的趋势,施工高度较低时响应谱毛刺较多。
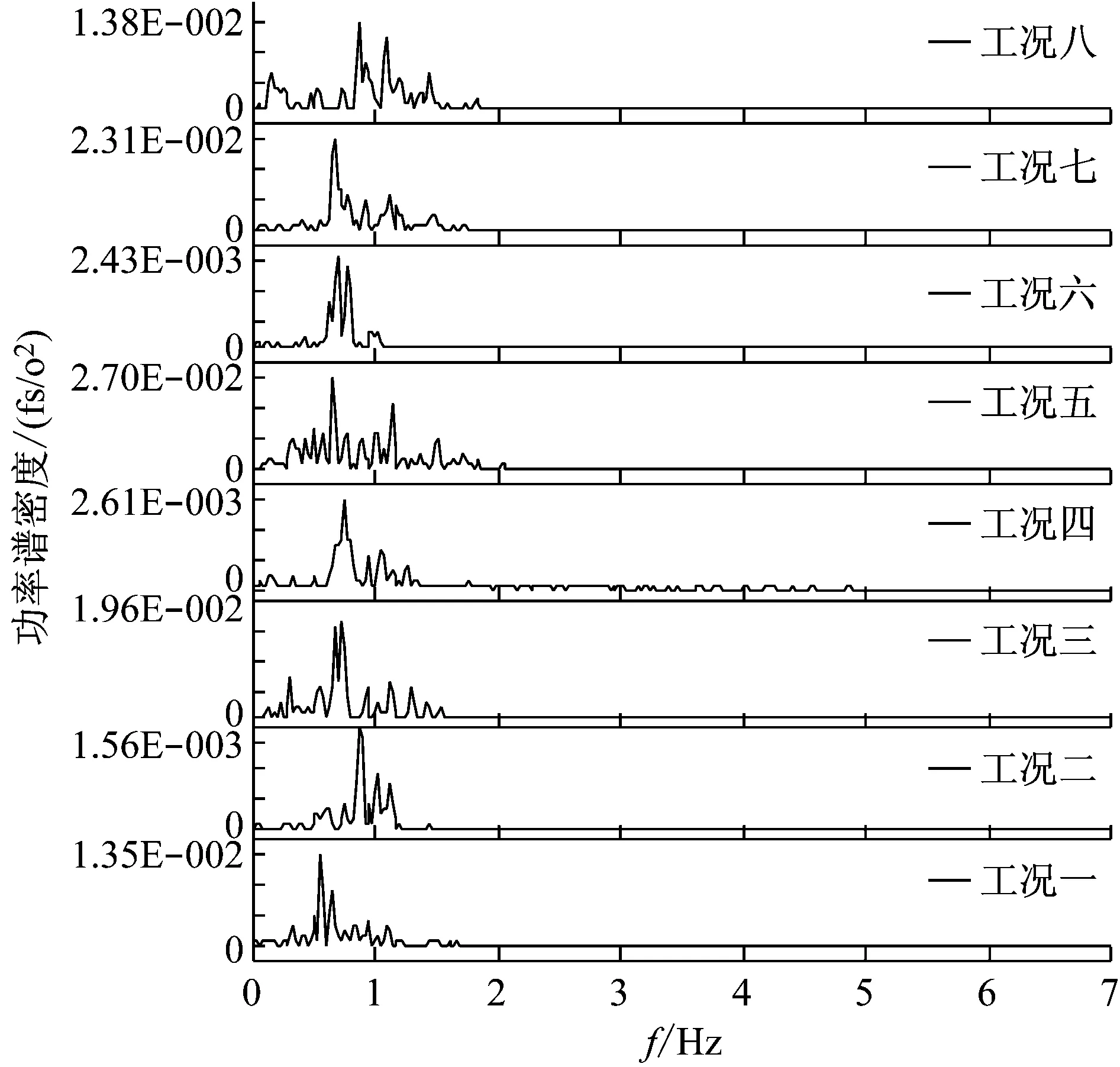
图11 超大型冷却塔施工全过程塔顶迎风面节点位移响应谱对比图
3.2.2 迎风面典型内力风振响应
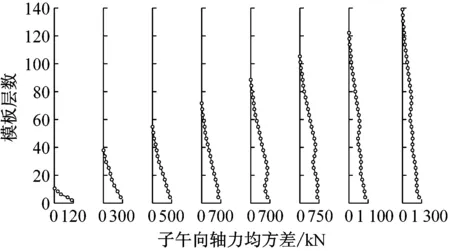
图12与图13分别给出了冷却塔子午向轴力与环向弯矩响应均值和均方差随施工高度变化示意图,对比发现随着施工高度的增长,各工况冷却塔子午向轴力和环向弯矩的均值与均方差分布范围均不断增长,但子午向轴力与环向弯矩均值和均方差数值均随着高度不断减小。当冷却塔施工高度较低时,环向弯矩变化呈现出折叠减小的趋势;冷却塔施工高度较高时,各工况冷却塔环向弯矩均方差在塔筒中上部出现突起。
(a) 子午向轴力均值
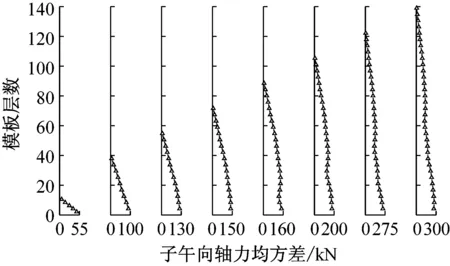
(b) 子午向轴力均方差
4 施工全过程风振系数分析
4.1 结构整体风振系数分布特征
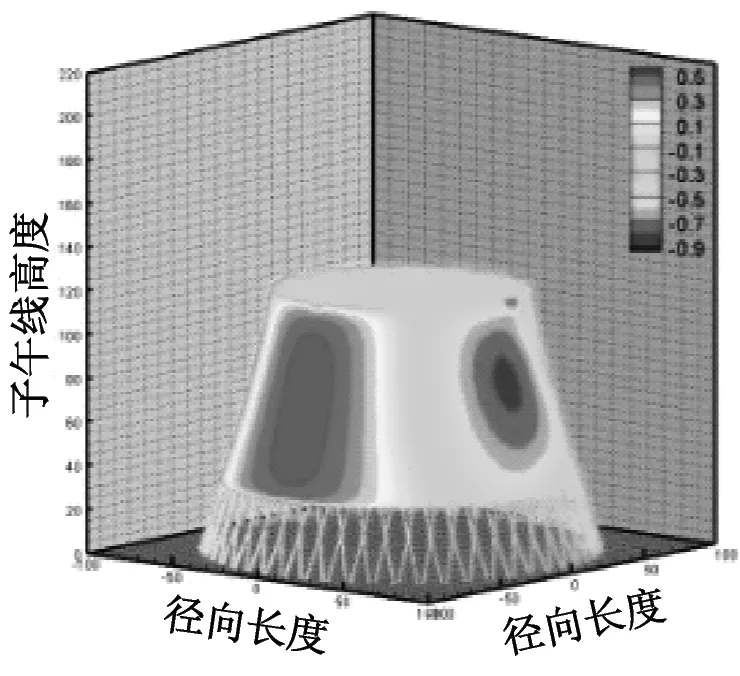
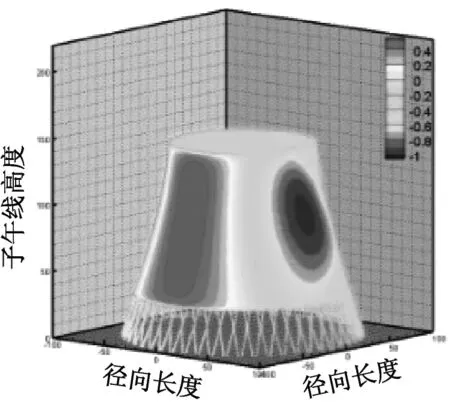
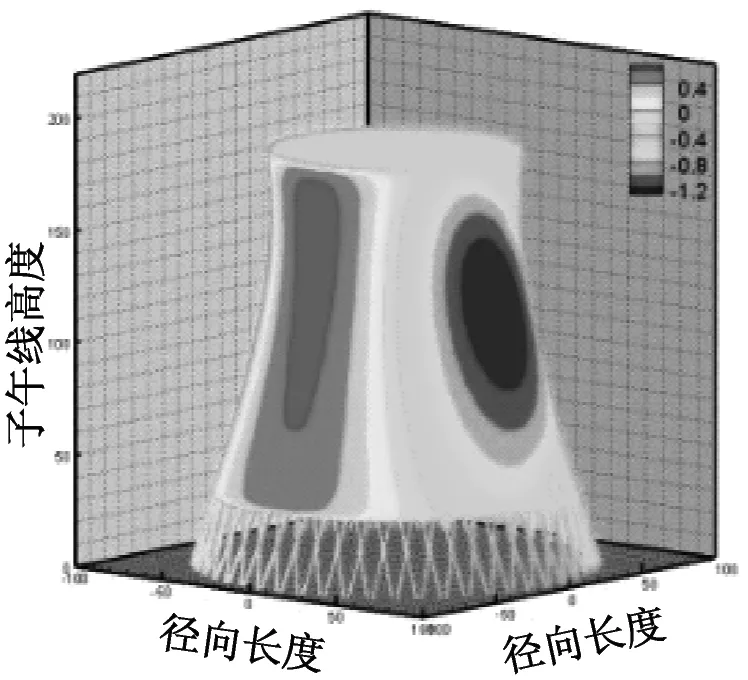
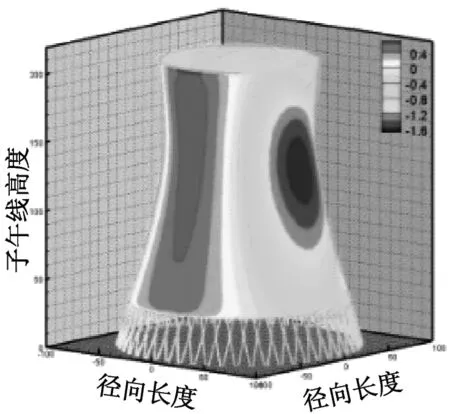
考虑冷却塔结构设计的控制内力,分别以径向位移、子午向轴力和环向弯矩三种响应为等效目标计算获得施工全过程各工况风振系数,图14~图16给出了这三种等效目标的不同工况风振系数三维分布图。对比分析发现单个冷却塔不同位置的风振系数并不统一,数值沿环向起伏较大,在平均风压较小的区域,如环向40°与120°附近,风振系数数值往往偏大,但是由于风压绝对值较小的原因,导致该区域的风振响应对整体结构响应影响较小。三种响应目标下各工况风振系数均在环向40°与120°附近出现极大值,但在子午向高度上风振系数极大值的位置有所提前或延迟。此外,未达到成塔工况时,由于没有上部刚性环的约束,导致结构上端出风口风振系数数值偏大,以子午向轴力和环向弯矩进行风振系数取值分析时该特征表现最为显著。
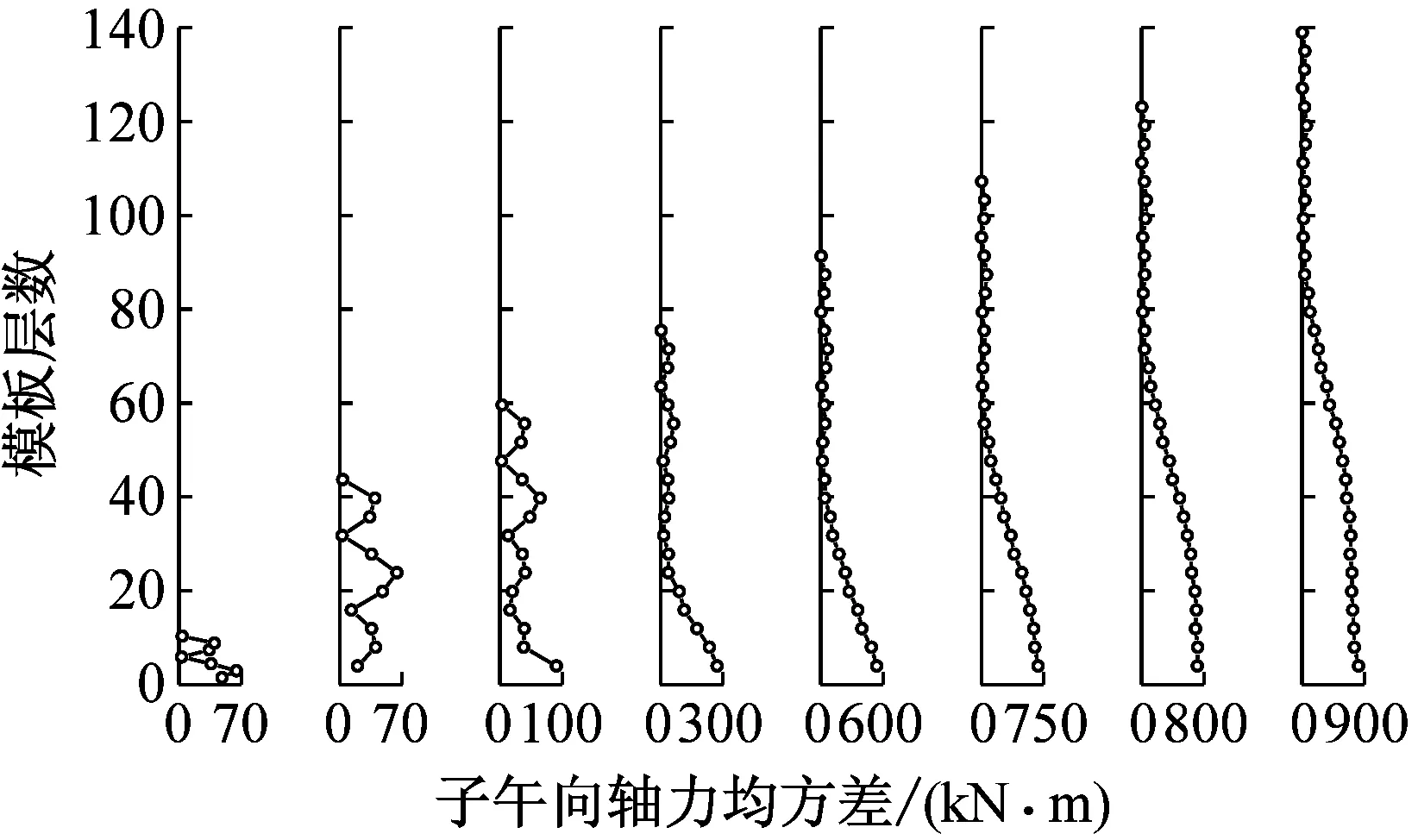
(a) 环向弯矩均值

(b) 环向弯矩均方差
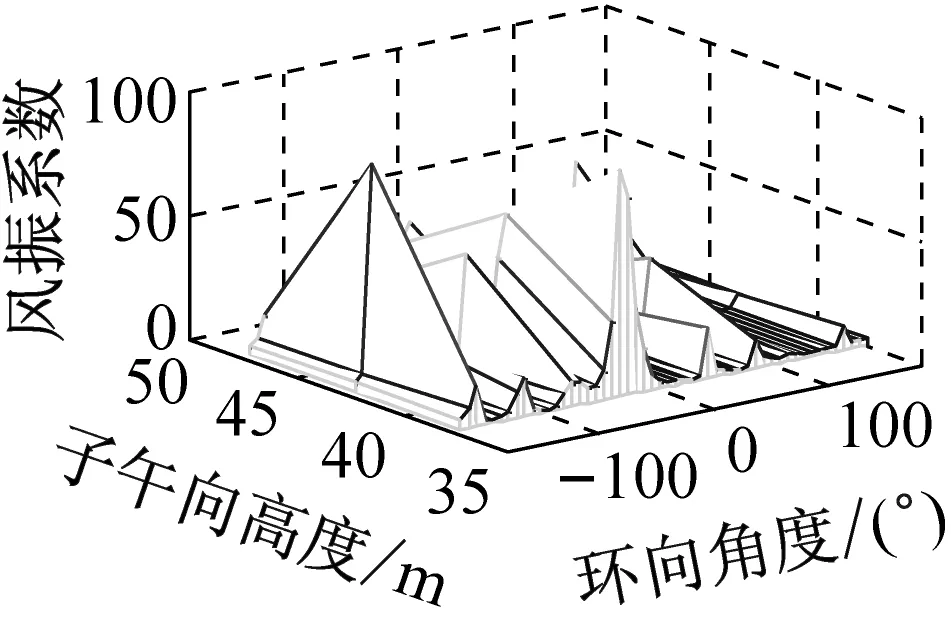
(a) 工况一
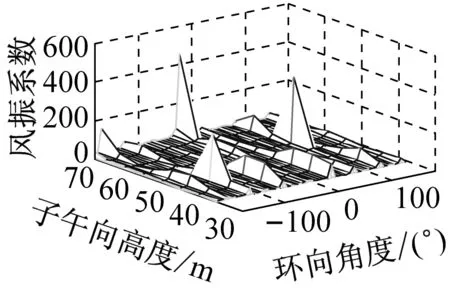
(b) 工况二
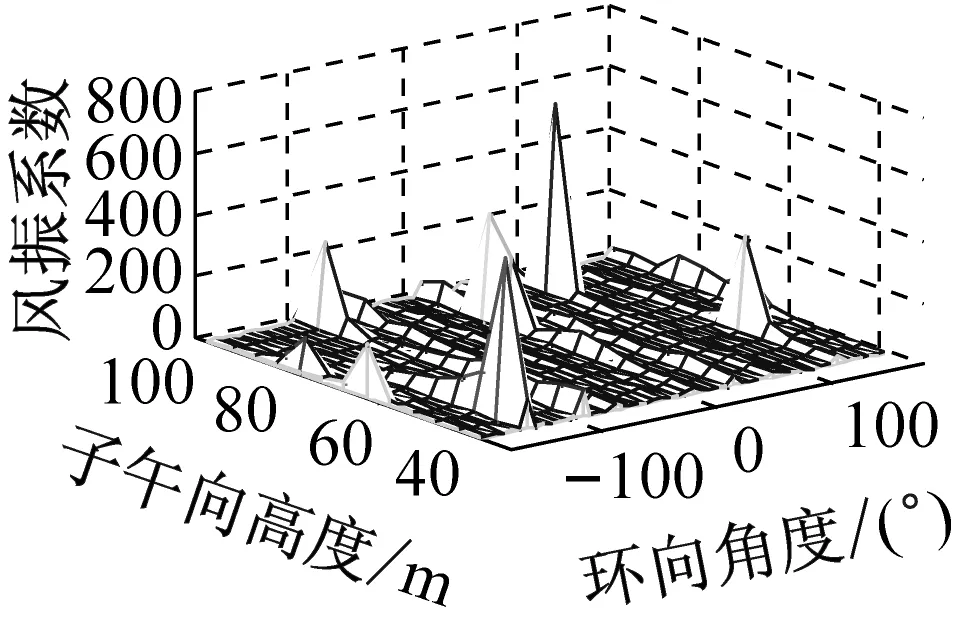
(c) 工况三
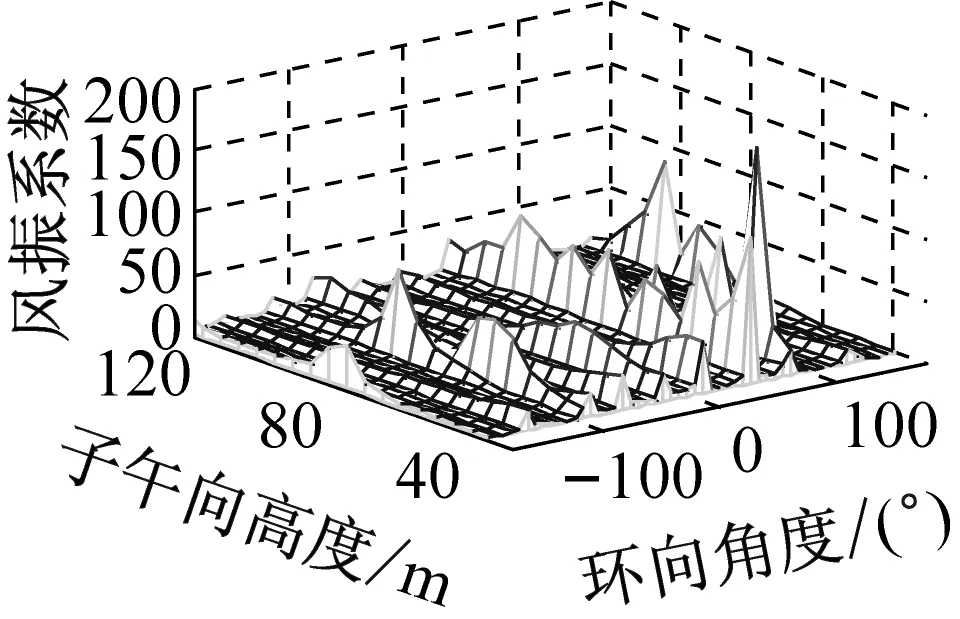
(d) 工况四
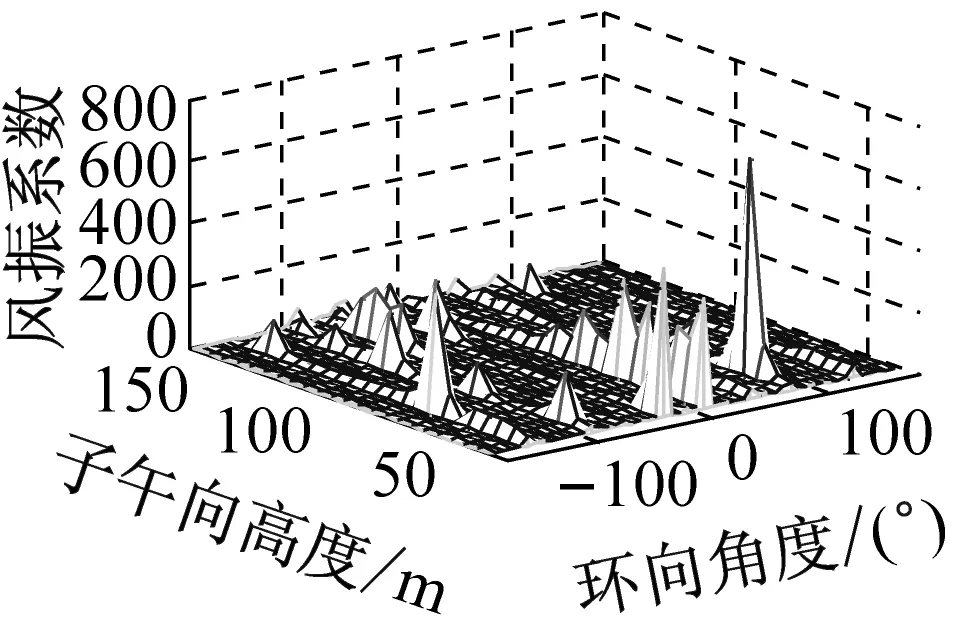
(e) 工况五
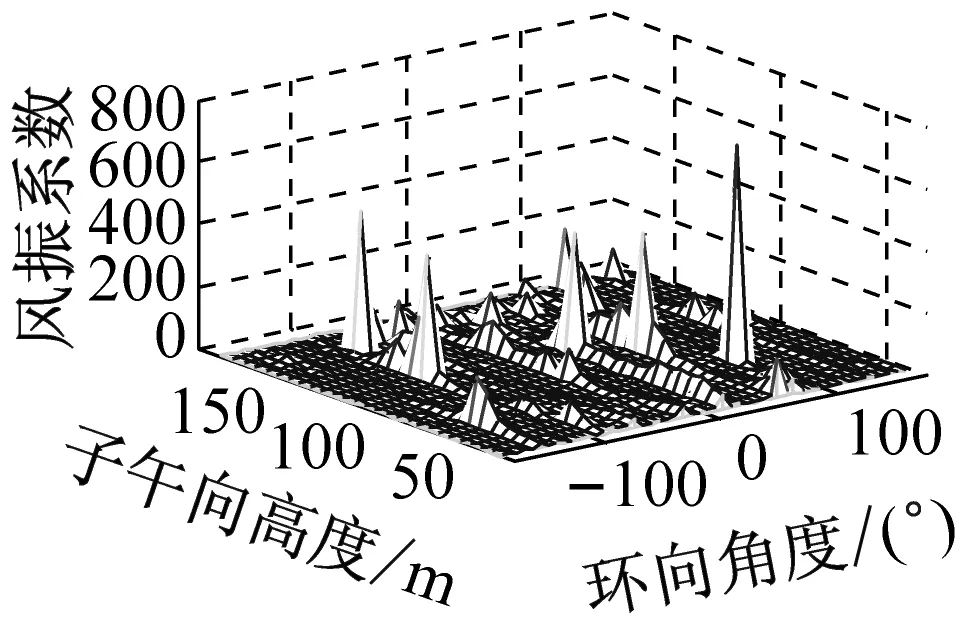
(f) 工况六
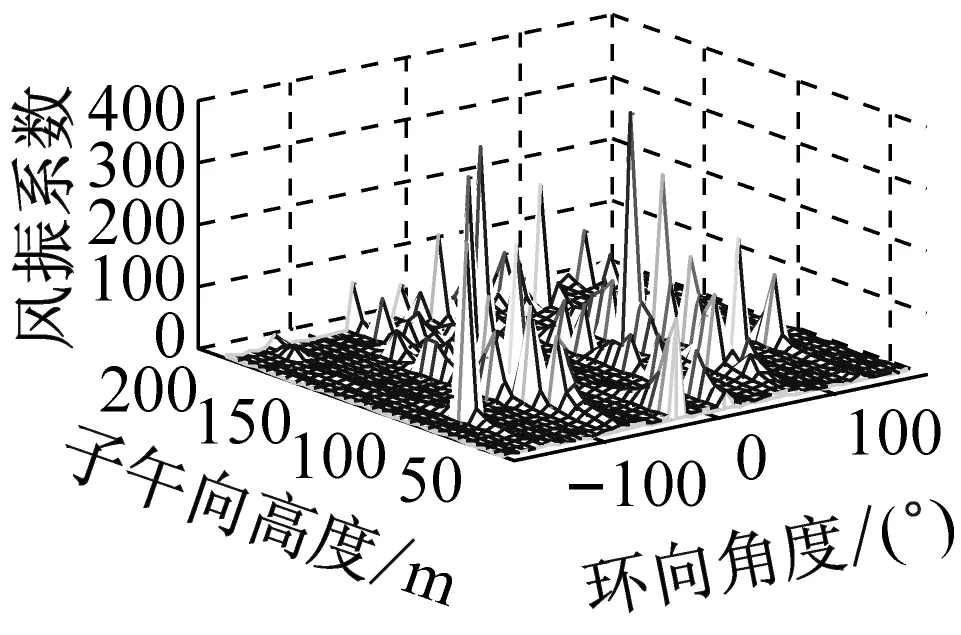
(g) 工况七
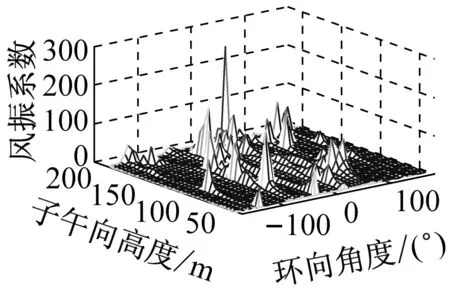
(h) 工况八
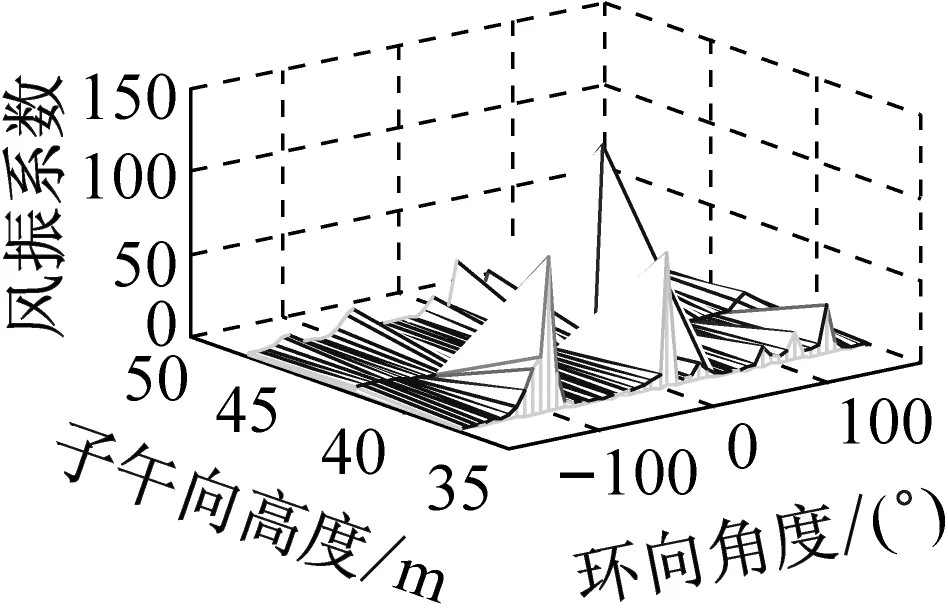
(a) 工况一
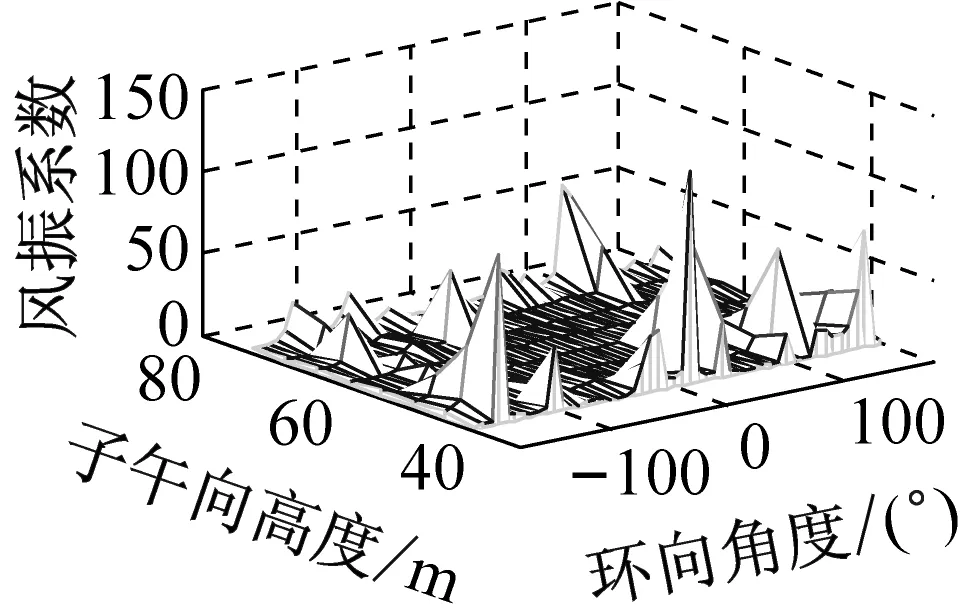
(b) 工况二
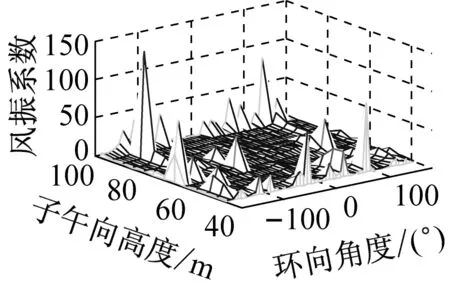
(c) 工况三
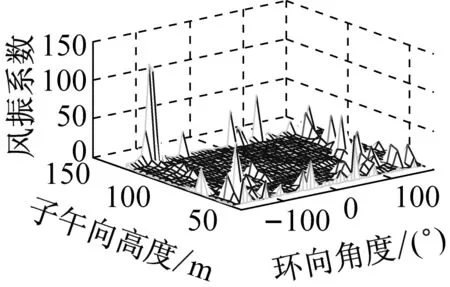
(d) 工况四
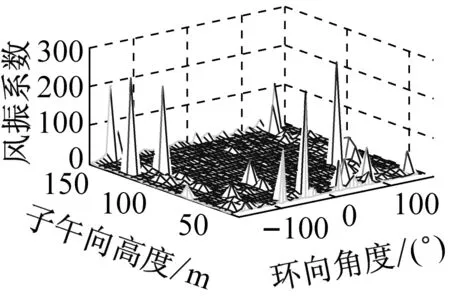
(e) 工况五
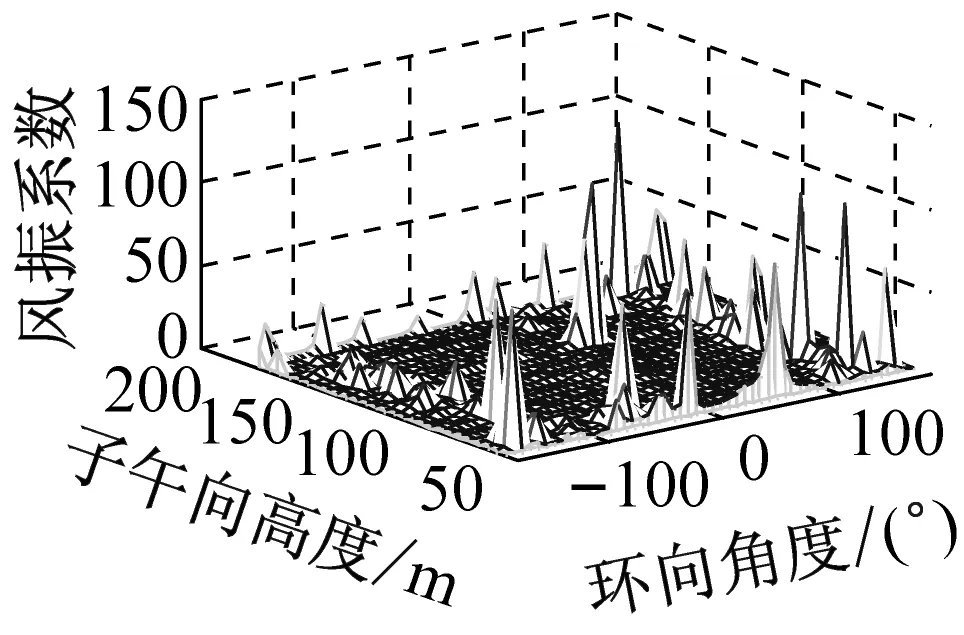
(f) 工况六
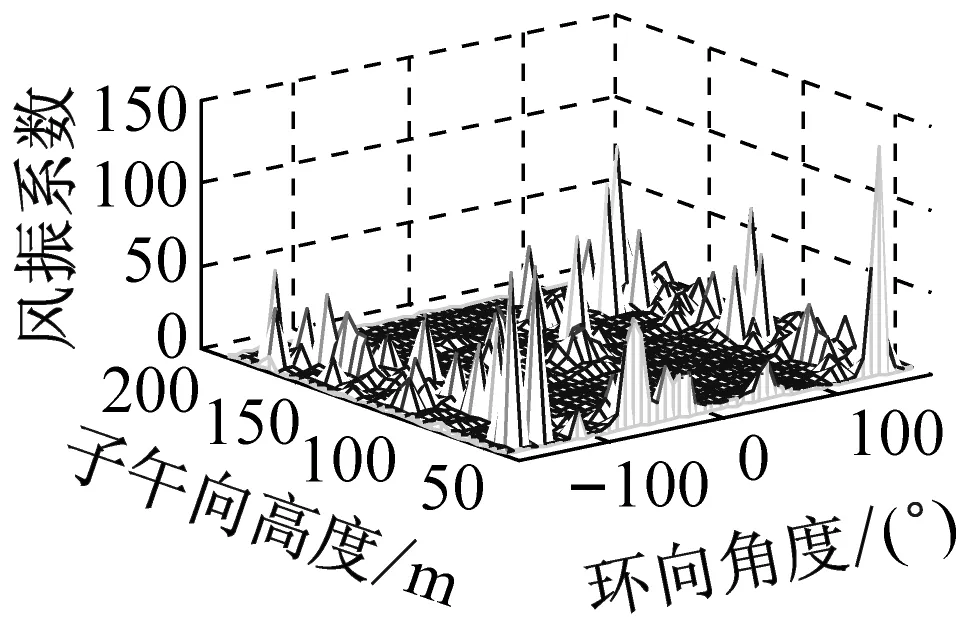
(g) 工况七
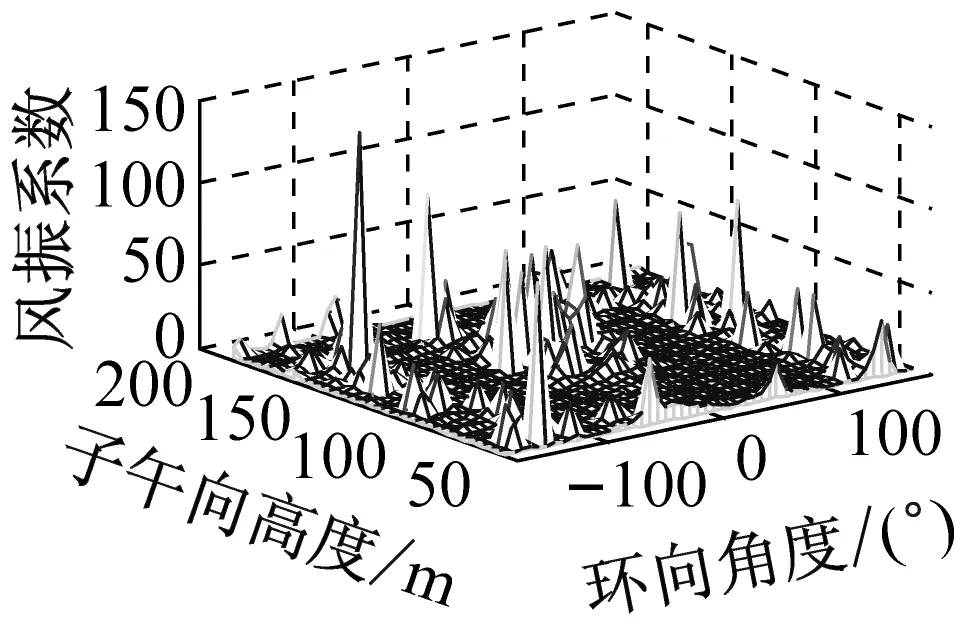
(h) 工况八
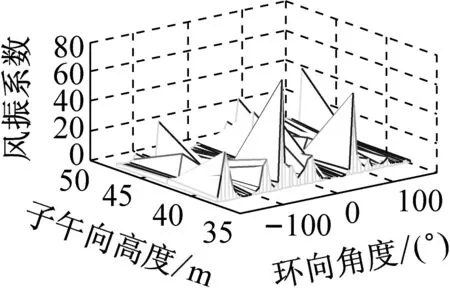
(a) 工况一
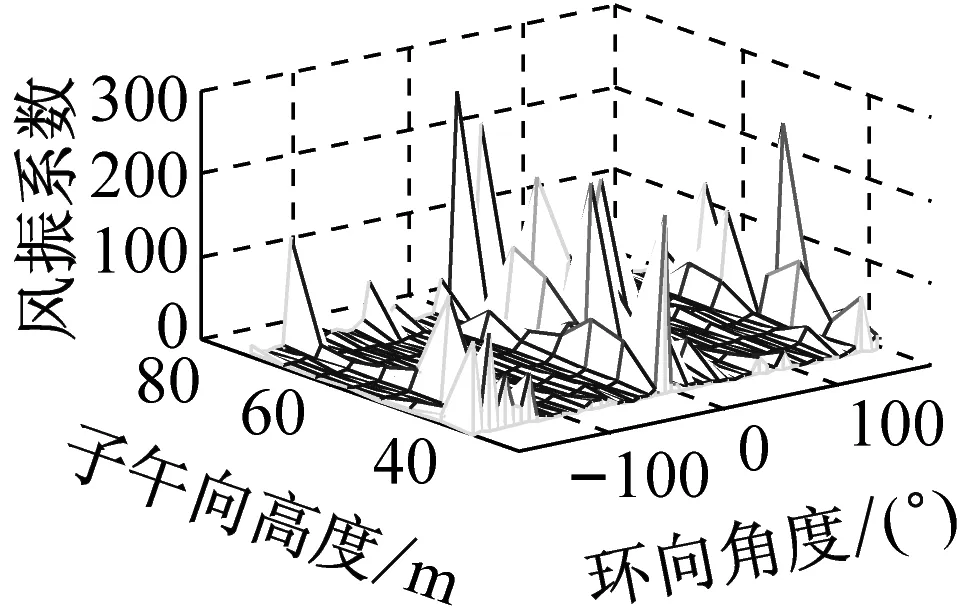
(b) 工况二
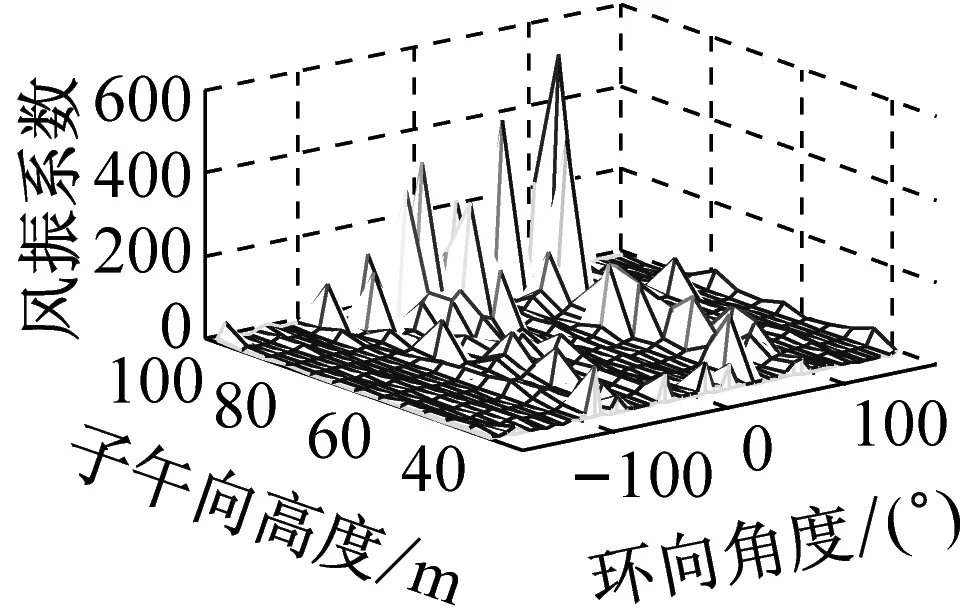
(c) 工况三
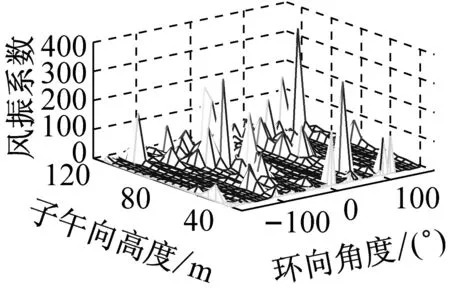
(d) 工况四

(e) 工况五
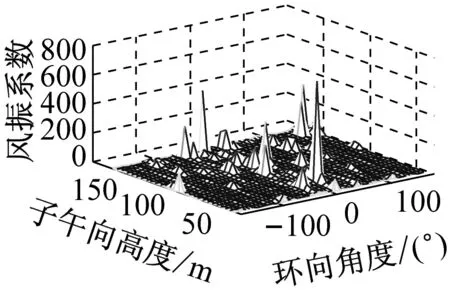
(f) 工况六
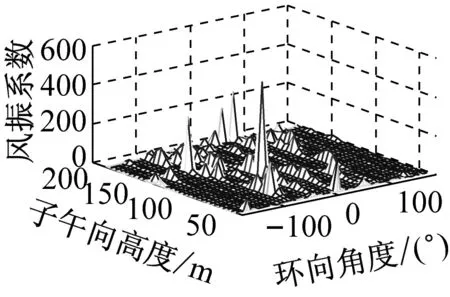
(g) 工况七
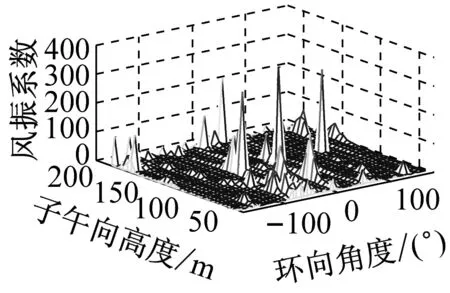
(h) 工况八
4.2 施工全过程风振系数取值
下面以五种常规主流的风振系数取值目标讨论施工全过程八个典型施工阶段风振系数的取值与变化趋势。
等效目标一:以迎风面子午向轴力为目标。冷却塔塔筒结构设计主要由子午向轴力控制,冷却塔规范的风振系数条款也是采用这一等效目标。
等效目标二:以迎风面Von Mises应力为目标。
等效目标三:以响应均值绝对值的平均值为目标,即提取冷却塔子午向轴力、环向弯矩及径向位移响应时程,统计各响应的平均值,再以该平均数为阈值,扣除目标响应均值小于阈值所对应的失真风振系数。
等效目标四:以响应均值绝对值的最大值为目标。
等效目标五:以最大风压系数*为目标,定义最大风压系数*=风振系数×∣风压系数∣,找出各层最大值所对应的位置坐标,然后计算每层最大风压系数*位置处的风振系数。
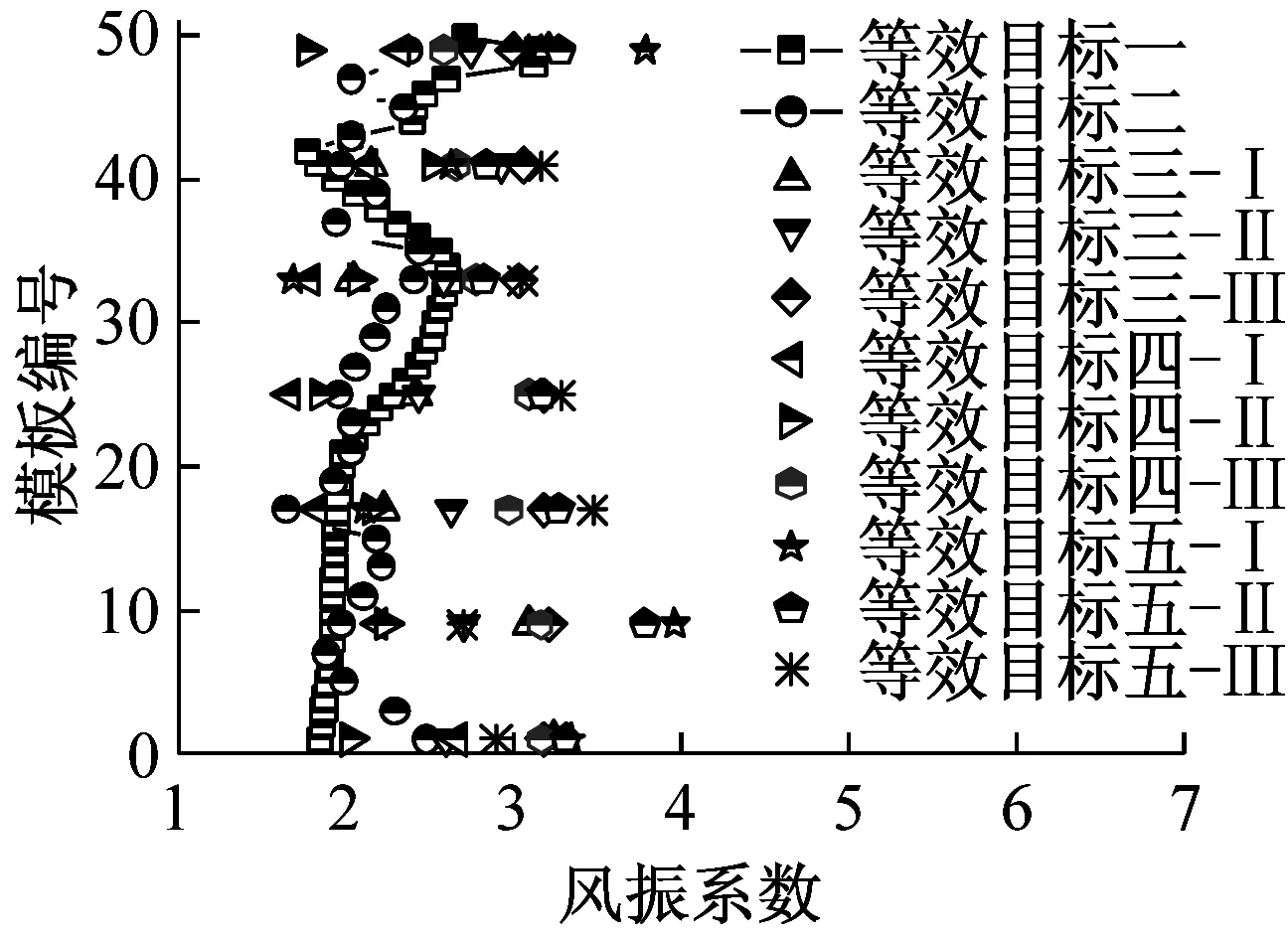
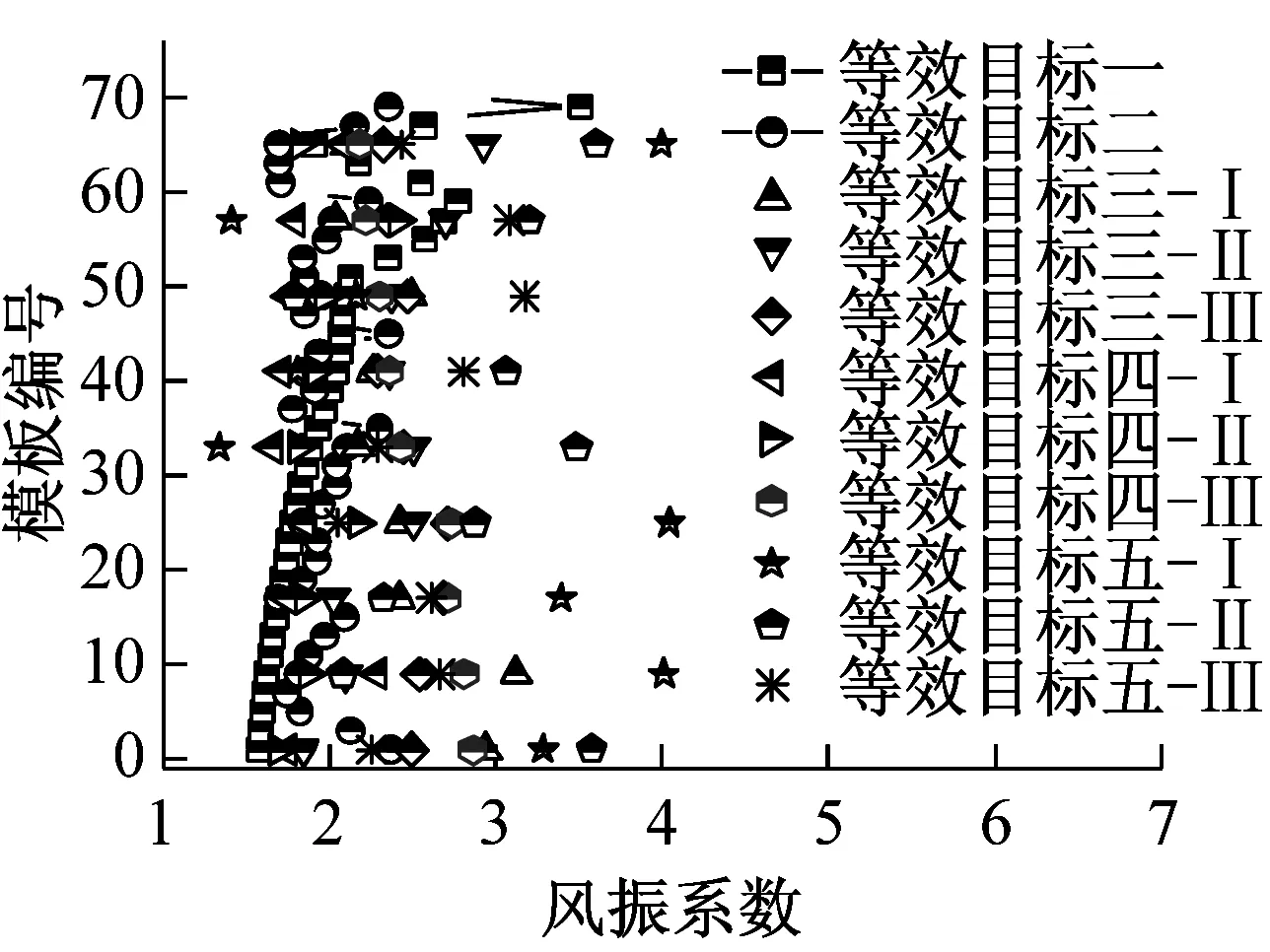
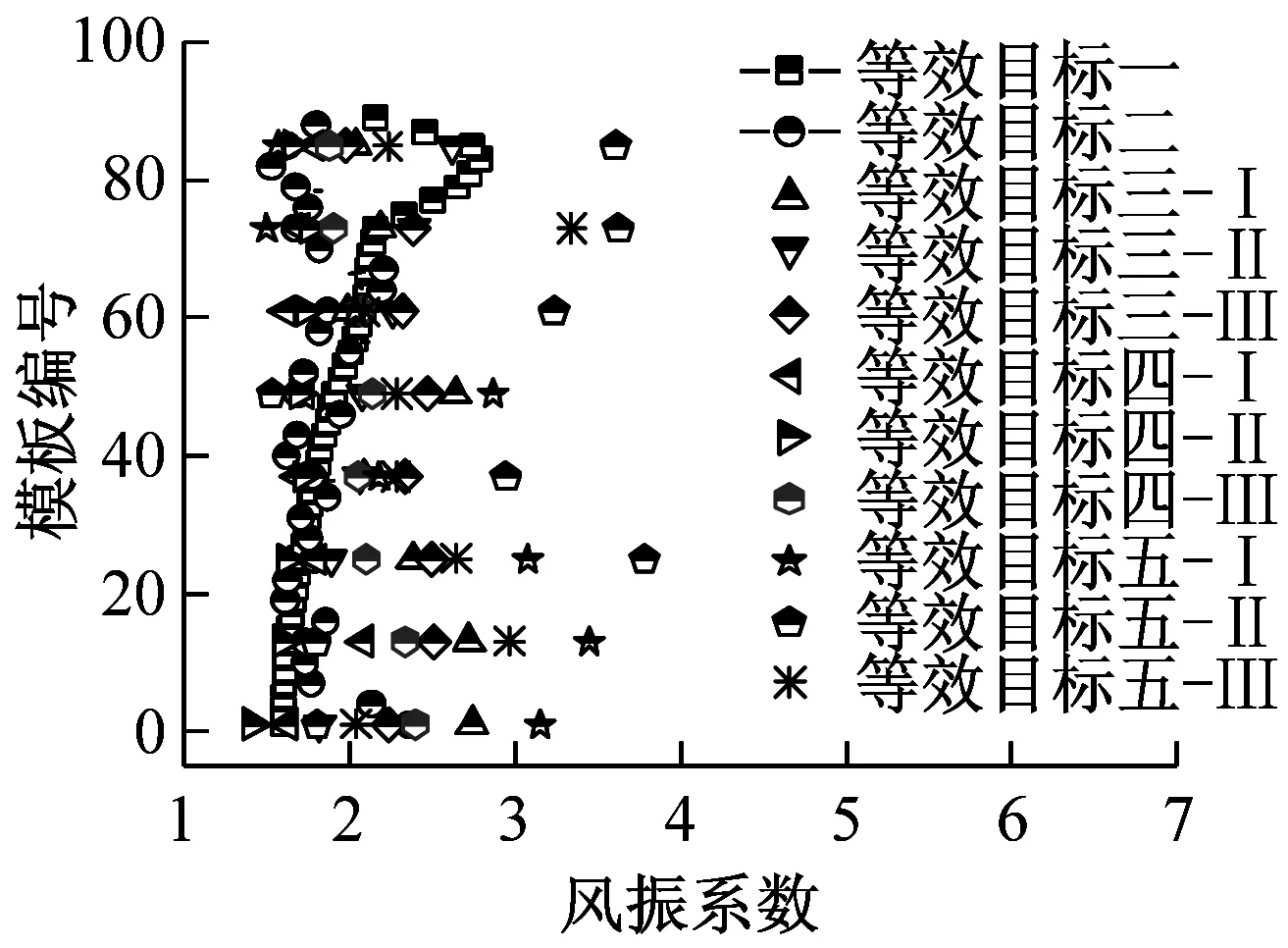
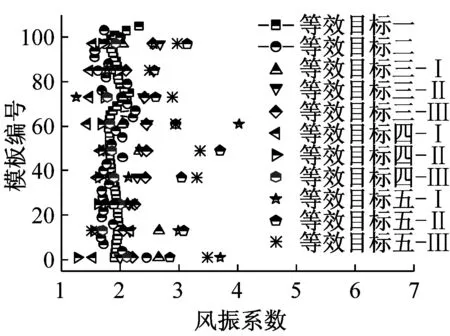
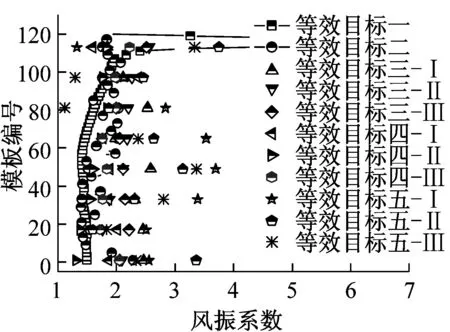
图17给出了五种风振系数取值目标下施工全过程风振系数沿高度分布示意图,对比发现八个施工工况下冷却塔风振系数沿塔高均呈现逐渐减小的趋势。针对同一个施工期模型,等效目标五获得的风振系数最大,等效目标一的风振系数最小。不同等效目标之间风振系数离散性较大,综合考虑结构控制内力和安全及经济性能,建议选取迎风面子午向轴力为等效目标进行施工全过程风振系数取值。
为方便工程实际应用给出施工全过程风振系数取值建议,图18汇总给出了五种等效目标下八个典型施工阶段冷却塔风振系数取值。
4.3 施工全过程风振系数拟合公式
综上分析可知,超大型冷却塔施工全过程风振系数受结构性能和风压分布等多种因素的影响,风振系数随塔高并未呈现出显著的线性增长关系。为方便科研、设计人员合理准确采用此类超大型冷却塔施工期风振系数,提出超大型冷却塔施工全过程以子午向轴力为目标(等效目标一,即规范等效目标)时风振系数的计算公式
(7)
式中:β0为成塔风振系数数值,β0=1.74;m、n与k为计算参数;x为施工模板层数;y为模板层数对应的风振系数取值。经过多次迭代计算得到超大型冷却塔施工全过程风振系数拟合公式中计算参数分别为:m=2.526,n=116.511,k=1.320。图19给出了风振系数拟合曲线与五种等效目标下的风振系数数值对比图,拟合曲线的数值及趋势分布能够很好地体现以子午向轴力为目标时施工全过程风振系数差异化取值。
5 结 论
本文系统研究了超大型冷却塔施工全过程风振响应和风振系数的演化规律,主要内容涉及大涡模拟、动力特性、风振响应、风振系数和参数分析等。得到主要结论如下:
(1) 采用LES方法获得了冷却塔施工全过程三维气动力时程,探讨了成塔迎风面、负压极值点、分离点及背风面测点脉动风压系数特性,并将平均和脉动风压与规范及国内外现有实测曲线对比验证了数值模拟的有效性。
(2) 不同施工高度对冷却塔结构频率影响较大,随着高度增加结构自振频率逐渐减小,同时不同模型的倾覆振型被激发的频率逐渐降低。不同施工高度对冷却塔模态振型影响较小,施工全过程冷却塔的最小固有频率均出现在4个环向谐波处。

(a) 工况一
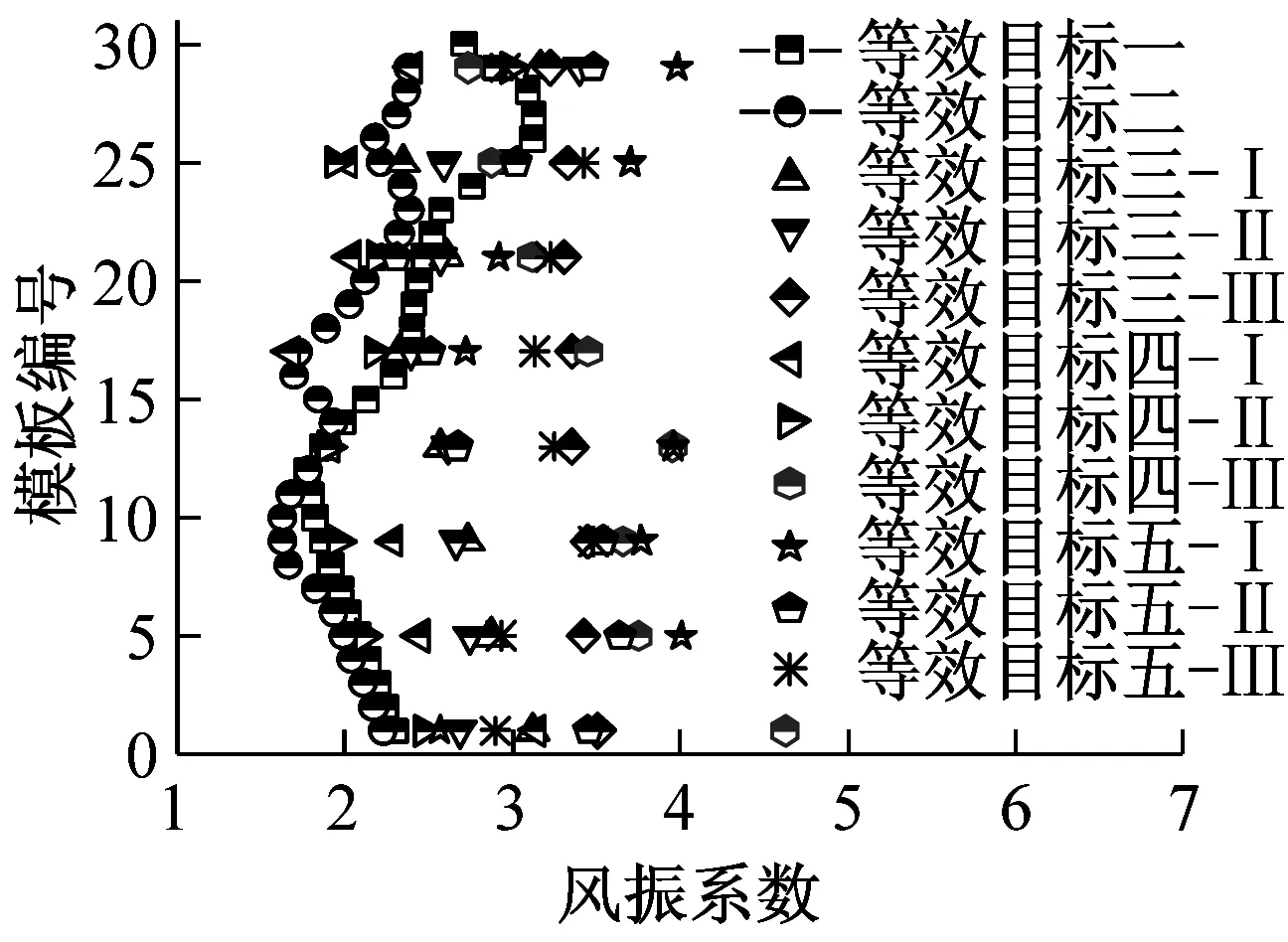
(b) 工况二
(c) 工况三
(d) 工况四
(e) 工况五
(f) 工况六
(g) 工况七
(h) 工况八
图18 五种等效目标下八个典型施工阶段冷却塔风振系数取值对比示意图
(3) 随着施工高度的增长,各工况冷却塔子午向轴力和环向弯矩的均值与均方差分布范围均不断增长,但子午向轴力与环向弯矩均值和均方差数值均随着高度不断减小。当冷却塔施工高度较低时,环向弯矩变化呈现出折叠减小的趋势;冷却塔施工高度较高时,各工况冷却塔环向弯矩均方差在塔筒中上部出现突起。
图19 超大型冷却塔施工全过程风振系数拟合曲线对比示意图
(4) 不同施工工况风振系数沿子午向和环向变化较大,但均在环向40°与120°附近出现极大值,但在子午向高度上风振系数极大值的位置有所提前或延迟。施工全过程冷却塔风振系数沿塔高均呈现逐渐减小的趋势,针对同一个施工期模型,等效目标五获得的风振系数最大,等效目标一的风振系数最小。
(5) 提出了超大型冷却塔施工全过程以子午向轴力为目标的风振系数计算公式(如下式,其中x为施工模板层数,y为对应施工模板层数的风振系数取值),简化公式能很好体现以子午向轴力为目标时施工全过程风振系数差异化取值。

