地表爆炸荷载作用下大型输水箱涵的毁伤评估及防护效应分析
杨广栋, 王高辉, 卢文波, 赵小华, 严 鹏, 陈 明
(1. 武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072; 2. 武汉大学 水工岩石力学教育部重点实验室,武汉 430072)
由于我国水资源在时空上分布不均,为了合理、充分地利用水资源,解决部分区域水资源短缺的问题,许多跨区域调水工程已建或正在建设,如南水北调、引滦入津、滇中引水、引江济淮等工程。其中南水北调工程是迄今为止世界上规模最大的调水工程,横穿长江、淮河、黄河、海河四大流域,涉及十余个省(自治区、直辖市),输水线路长,输水结构多(渡槽、箱涵、泵站等),工程涉及面广,投资巨大,政治经济等效益显著。然而近年来世界范围内恐怖袭击和意外爆炸事件频繁发生,使人们意识到突发爆炸荷载将对输水结构的安全构成巨大的威胁。一旦输水结构某处遭受破坏,可能导致整条输水线路瘫痪,且短时间内难以修复,同时会给国家造成巨大的经济损失和非常恶劣的政治影响。因此,研究南水北调工程中输水结构在爆炸荷载作用下的毁伤特性,对结构的抗爆防护设计及应急方案的采取都具有重要的指导意义。
跨区域调水工程中,为了跨越沟壑或减少开挖,以保护环境、降低造价,或出于线形要求,亦或是城市规划的需要,经常要采用钢筋混凝土箱涵作为输水结构。如果箱涵穿过城市、公路或交通便利的场所,则极有可能遭受汽车爆炸的袭击。而爆炸荷载作用下箱涵结构的破坏又是一个十分复杂的过程,当前对于输水箱涵的研究主要还集中在常规荷载作用下箱涵的应力、变形分析[1-3]。对于爆炸荷载作用下箱涵结构的动力响应研究也仅仅只是针对地下爆破荷载对箱涵安全性能的影响。如崔溦等[4-5]采用二维SPH-FEM耦合的方法研究了土中爆炸冲击荷载对大型输水箱涵安全性的影响。而目前关于地表爆炸荷载作用下结构的动力响应研究主要是集中在地下隧道结构。如善生彪等[6]通过运用有限元Midas/GTS软件分析了不同接头的隧道管片在爆炸荷载作用下的变形、振速及内力分布特征;Mussa等[7]研究了不同埋深、不同厚度的箱形隧洞在不同TNT当量作用下的毁伤破坏特征;Mobaraki等[8]利用LS-DYNA有限元软件研究了1 000 kg TNT当量炸药作用下不同埋深、不同形状断面地铁隧道的动力响应,结果显示半椭圆形隧道具有较好的抗爆性能;De等[9-10]通过模型试验和数值模拟的方法研究了地表爆炸荷载作用下地下隧道的变形特征,同时探讨了聚氨酯土工泡沫对其抗爆性能的影响。但关于地表爆炸荷载作用下大型输水箱涵的毁伤评估及防护措施仍缺乏系统的研究。
本文首先通过与已有的经验公式和现场试验进行对比,分别验证了地表爆炸模型和钢筋混凝土模型的可靠性。随后基于该方法建立了地表爆炸荷载作用下钢筋混凝土箱涵全耦合模型,探讨了地表爆炸荷载对地下输水箱涵结构安全性能的影响,对比分析了箱涵正常输水和内部无水两种条件下爆炸冲击波的传播过程、箱涵结构的非线性动态响应行为以及毁伤空间分布特征。同时,提出了在箱涵顶部铺设一定厚度的聚苯乙烯泡沫,研究其对提高混凝土箱涵抗爆性能的作用。
1 材料模型及状态方程
1.1 材料动态本构模型
在爆炸等极端荷载作用下,混凝土材料通常会出现应变率效应。本文采用RHT[11]模型模拟混凝土箱涵在地表爆炸荷载作用下的损伤发展过程。该模型除了具有压力依赖性、应变速率敏感性和压缩损伤软化等特点外,同时引入了偏应力张量第三不变量对破坏面形状的影响,考虑了拉静水区和压静水区应变率敏感性的差异性。RHT模型中引入了弹性极限面、失效面及残余强度面作为3个控制破坏面以描述混凝土材料的初始屈服强度、失效强度和残余强度,如图1所示。RHT模型主要参数如表1所示。
RHT模型失效面方程为
(1)
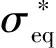
(2)
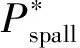
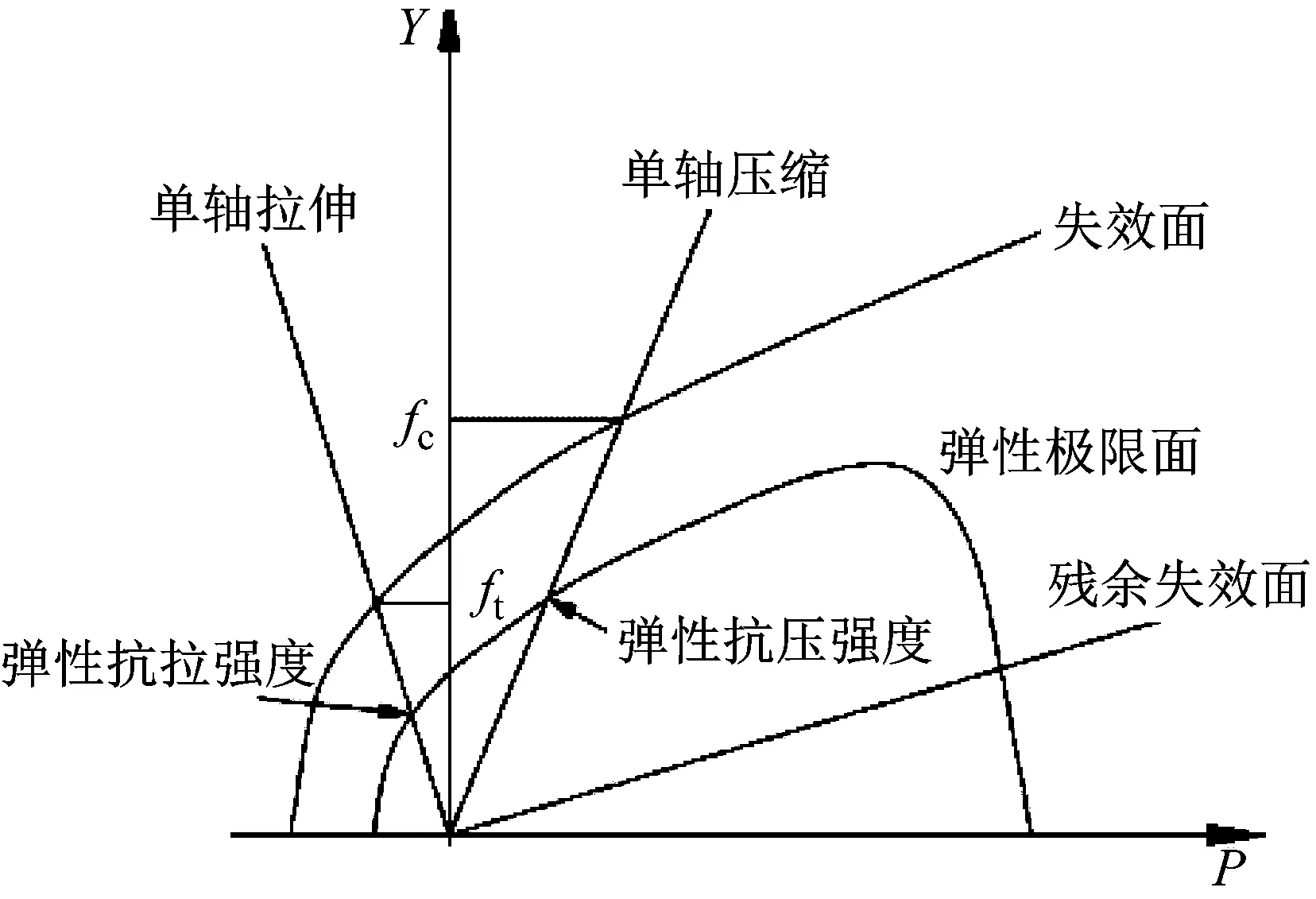
图1 RHT本构模型的三个失效面
RHT本构模型的损伤定义为
(3)
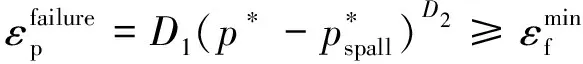
(4)
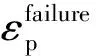
采用Johnson-Cook本构模型描述钢筋在高温、大变形、高应变率下的应力、应变关系[12]
(5)
TH=(T-Troom)/(Tmelt-Troom)
(6)
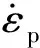
采用AUTODYN中SAND材料描述爆炸荷载作用下土体的应力与变形特性[13]。土体密度1 920 kg/m3,表3为土体的体积应变随压力的变化规律。
采用线性黏弹性模型描述冲击荷载作用下EPS材料的动力响应。该模型采用不同的剪切模量描述EPS材料在不同状态下的力学行为

表1 混凝土RHT模型主要参数

表2 钢筋材料参数表

表3 土体体积应变与压力关系表

(7)
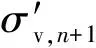
1.2 状态方程
采用JWL状态方程模拟炸药爆炸过程中压力和内能及相对体积之间的关系
p=A1(1-ω/R1V)e-R1V+B1(1-
ω/R2V)e-R2V+ωE0/V
(8)
式中:p为爆轰压力,V为爆轰产物的相对体积(爆轰产物体积和炸药初始体积之比),E0=6.0 GJ/m3,ρ=1 630 kg/m3,D=6 930 m/s,Pcj=21 GPa,V0=1.0,A1=373.77 GPa、B1=3.75 GPa、R1=4.15、R2=0.90、ω=0.35为材料常数。
对于水体采用Polynomial状态方程
当水压缩时(μ﹥0),状态方程为
P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e
(9)
当水膨胀时(μ﹤0),状态方程为
P=T1μ+T2μ2+B0ρ0e
(10)
式中:P为水中压力;μ为压缩比,μ=ρ/ρ0-1;e为水的内能;ρ0为水密度,取为1 g/cm3;A1=T1=2.2×106kPa,A2=9.54×106kPa,A3=1.46×106kPa,B0=B1=0.28,T2=0。
空气采用Ideal Gas状态方程
P=(γ-1)ρe
(11)
式中:ρ为空气密度,取1.225 kg/m3;e为空气初始内能;γ为材料常数,取1.4。
聚苯乙烯塑料板采用Shock状态方程
Us=C1+S1up
(12)
式中:Us为冲击波传播速度,up为质点振动速度,C1、S1为材料常数,C1=2 400 m/s,S1=1.319。详细的本构模型及参数描述可以参考文献[14-15]。
2 地表爆炸全耦合模型验证
2.1 地表爆炸模型验证
为了验证土体表面炸药爆炸模型的合理性及准确性,采用Eulerian方法建立了半无限土体地表爆炸模型,对地表爆炸荷载作用下冲击波在土体中的传播过程进行模拟,并将模拟结果与经验公式(TM5-855-1)[16]对比。选取模型尺寸为20 m×20 m×20 m,空气计算域取4 m,土体计算深度取16 m,TNT炸药量为1 250 kg。因模型具有对称性,为节约计算时间,采用1/4模型进行计算,如图2。网格尺寸0.2 m,网格数量总
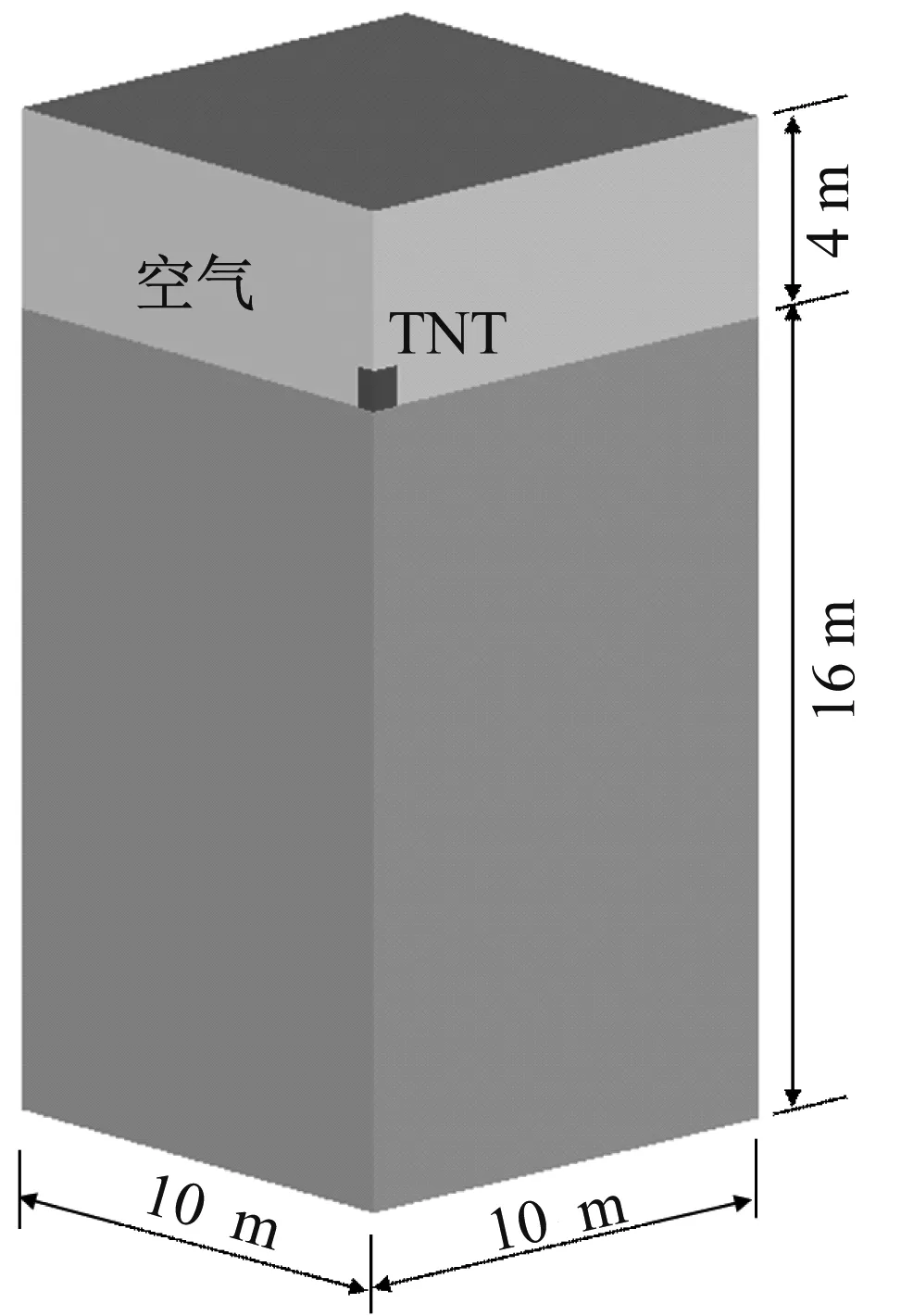
图2 土体表面爆炸计算模型
计250 000,在对称面上施加对称边界,其余四个面均施加无反射边界。
由美国陆军工程师手册(TM-5-855-1)提出的预测不同土体、不同埋深条件下,土中压力峰值变化的经验公式
(13)
式中:Pp为土中的峰值压力;f为耦合系数,对于地表爆炸可取0.14;R为土中测点距爆源的距离;W为炸药的质量;ρc为土体的声阻抗;n为衰减系数。
表4给出了不同类型土体的峰值压力预测参数,本文选取第四类型的土体参数(回填土),利用式(13)来预测地表爆炸荷载作用下不同深度处土体内部的峰值压力。
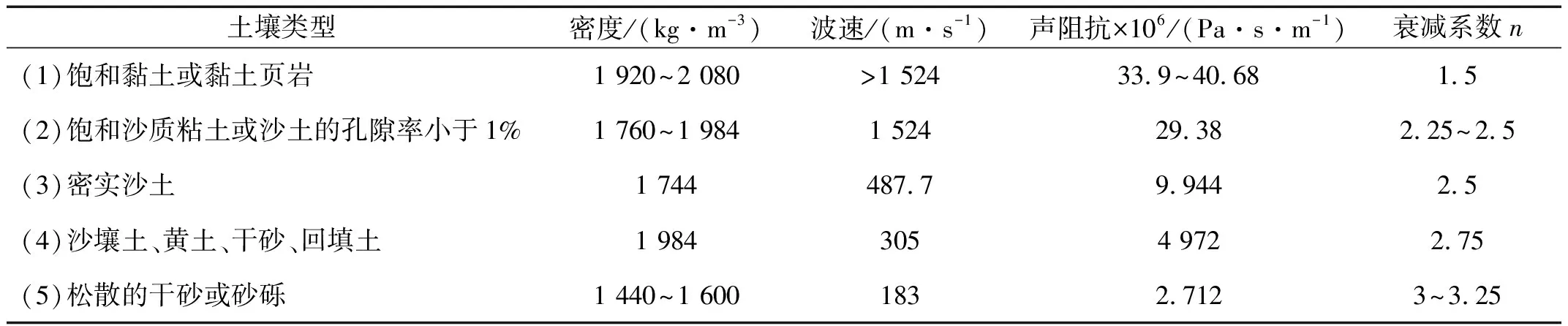
表4 不同类型土体的参数(TM-5-855-1)
图3给出了1 250 kg TNT炸药在地表爆炸时土体中峰值压力随比例距离的变化规律。在爆源近区,冲击波压力峰值很高,达到了几百兆帕;随着距离的增大,峰值压力迅速衰减。将数值计算的结果与经验公式(TM-5-855-1)进行对比,可以发现二者吻合的很好,说明采用当前的土体模型和材料参数可以较好地模拟爆炸冲击荷载在土体中的传播特性。
2.2 钢筋混凝土模型验证
为了验证爆炸荷载作用下钢筋混凝土模型的可靠性,对参考文献[17]中的现场爆炸试验进行模拟再现。该试验中采用的钢筋混凝土板边长为1 000 mm,厚度为40 mm。炸药TNT当量为310 g,置于钢筋混凝土板的正上方,距离板上表面中心400 mm,如图4(a)。在混凝土板底部布置单层受力钢筋,钢筋直径6 mm,间距75 mm,保护层厚度10 mm,如图4(b)。混凝土的抗压强度39.5 MPa,抗拉强度4.2 MPa,弹性模量28.3 GPa。钢筋的屈服强度为600 MPa,弹性模量200 GPa,剪切模量82 GPa。

(a) 试验装置图
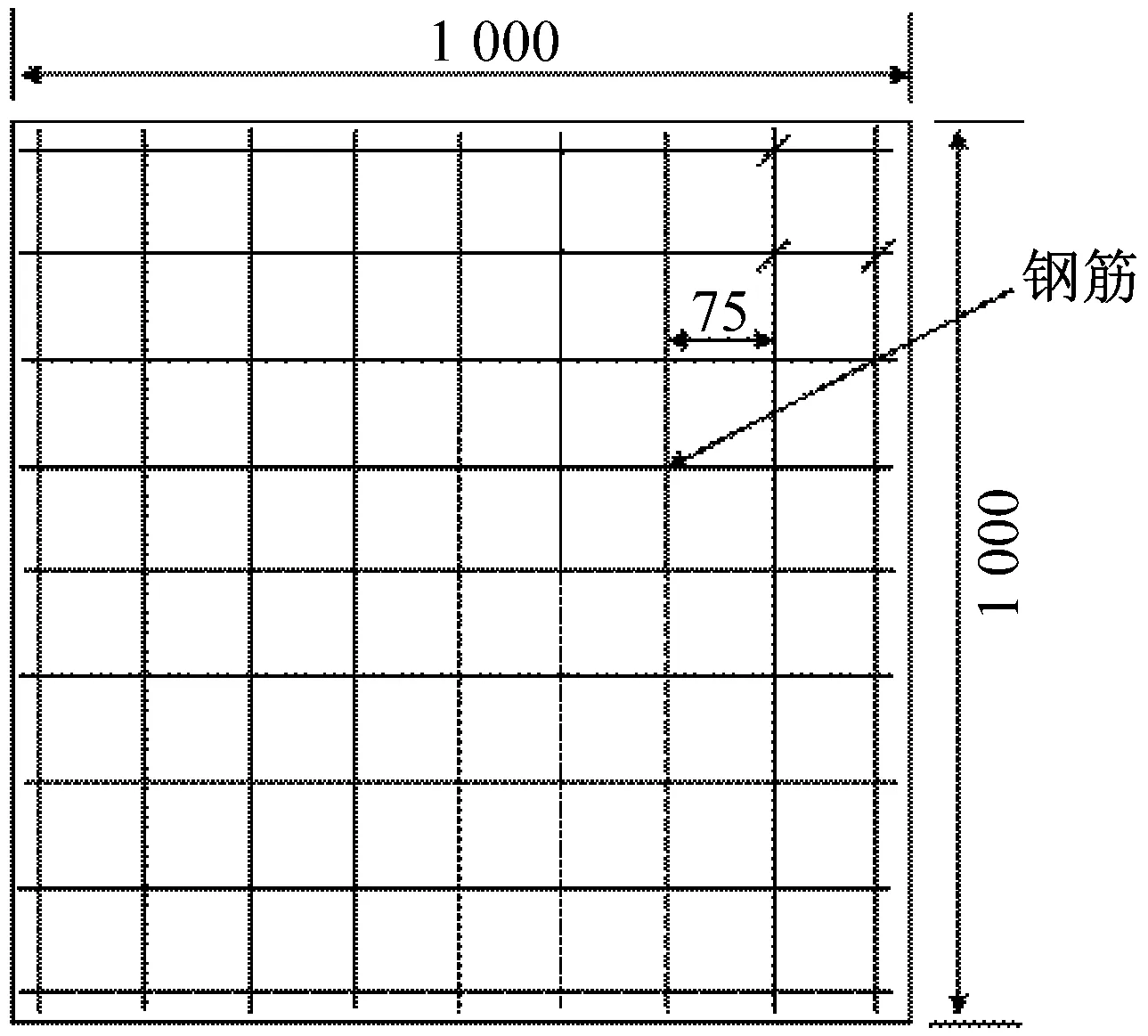
(b) 钢筋布置图
因模型具有对称性,为节约计算成本,采用1/4模型进行计算分析。该模型包括炸药、空气、混凝土、钢筋四种材料的耦合,如图5。炸药和空气均采用Eulerian单元,混凝土材料使用Lagrangian单元,钢筋采用Beam单元。采用流固耦合的方法描述空气与混凝土材料之间的相互作用,钢筋与混凝土材料之间的相互作用通过节点耦合的形式实现。空气、炸药和钢筋的网格尺寸均为10 mm,混凝土板的尺寸为5 mm。在空气区域外表面施加无反射边界条件,混凝土板的两端施加固定约束。
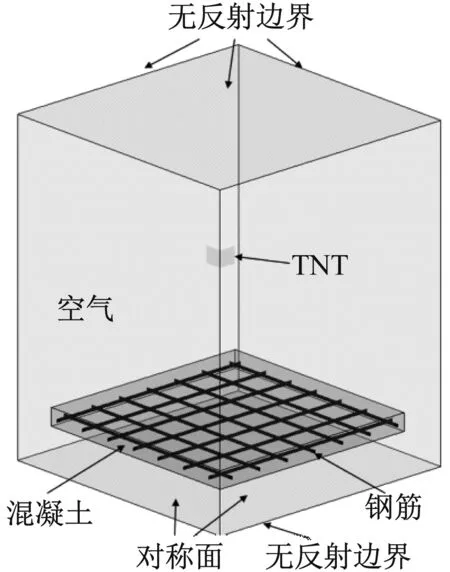
图5 爆炸试验有限元模型
图6为钢筋混凝土损伤分布的数值计算结果与现场试验结果的对比图。由图可以看出,数值计算的混凝土板正面和背面的损伤分布与现场试验结果均吻合较好,说明本文采用的RHT本构模型及参数可以较好地描述爆炸冲击荷载作用下钢筋混凝土结构的动力响应特性。


(a) 迎爆面损伤分布图


(b) 底面损伤分布图
3 爆炸荷载作用下箱涵的毁伤特性分析
3.1 箱涵全耦合数值模型的建立
以南水北调中线工程中典型的钢筋混凝土箱涵为研究对象,该模型包括钢筋、混凝土、TNT炸药、土体、水、空气六种材料的耦合,如图7(a)。箱涵采用两孔一联,孔径尺寸为4.4 m×4.4 m,单段箱涵长度15 m,箱涵底板厚0.6 m,顶板、边墙、中墙厚度均为0.5 m,考虑到模型对称性,为减少计算时间,选取1/2模型为研究对象,如图7(b)。箱涵的配筋采用双向双层布置方式,钢筋直径18 mm,间距20 cm,保护层厚度10 cm,如图7(c)。箱涵埋深为2.0 m,炸药放置于箱涵正上方,考虑到箱涵的受袭方式可能是小型货车的爆炸袭击,故TNT当量取为1 250 kg。
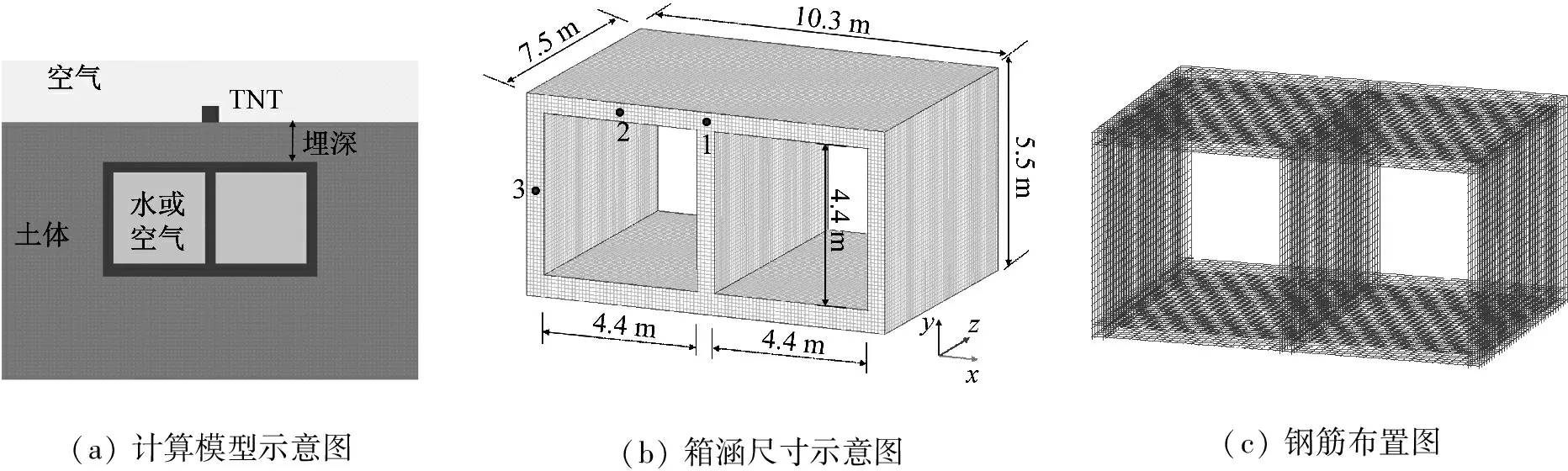
箱涵输水工况非常复杂,以满孔输水作为箱涵运行的正常工况。由于水压力相对于爆炸冲击荷载很小,故不考虑水压力对箱涵的作用。同时,为了研究地表爆炸荷载作用下,箱涵内部水荷载对其受力特性的影响,本文还对比研究了爆炸荷载作用下,内部无水条件下箱涵的动力响应及其损伤发展过程。
爆炸荷载作用下的箱涵结构动态响应及其破坏是一个复杂的过程,涉及炸药的起爆、冲击波的传播、冲击波与自由面及结构面的动态耦合作用以及随后结构的动态响应等过程。目前用于描述爆炸荷载作用下结构动力响应的方法主要有Lagrangian方法、Eulerian方法。为了描述爆轰产物的扩散过程以及土体的大变形等问题,采用Eulerian方法描述空气、炸药、土体和水在爆炸荷载作用下的行为特征。该方法以空间坐标为基础,网格在整个分析过程中始终保持空间位置不动,物质在网格中流动,非常适用于描述流体或部分结构的大变形问题。采用Lagrangian方法描述混凝土箱涵在爆炸冲击荷载作用下的动力响应,该方法的结构变形与网格变形一致,能够精确地描述结构的边界运动,与Eulerian算法相比计算速度较快。Eulerian网格与Lagrangian网格之间采用CEL(Coupled Eulerian-Lagrangian Method)算法连接,该算法的一般策略是把Eulerian网格看作是Lagrangian网格的压力边界条件,把Lagragian网格看作是Eulerian网格的速度边界条件[18]。
采用Lagrangian-Eulerian耦合方法研究地表爆炸荷载作用下钢筋混凝土箱涵的动力响应及毁伤特征。Eulerian网格单元尺寸为200 mm,网格总数333 000;混凝土材料单元尺寸取100 mm,网格总数130 000;钢筋采用Beam单元,钢筋单元尺寸为100 mm,单元总数53 000。钢筋与混凝土材料之间通过节点耦合的方式实现,不考虑二者之间的相互滑动。在对称面上施加对称边界,其余的Eulerian网格边界上均施加无反射边界条件,使得人工边界上无应力波反射,以模拟半无限区域。
3.2 箱涵毁伤特性分析
图8给出了箱涵正常运行工况下,爆炸冲击波在土体、箱涵及水体中的传播过程。炸药起爆后,近似半球形的爆炸冲击波开始从炸药处向外围的土体传播;炸药起爆约3 ms后,冲击波传至箱涵顶板底面,一部分以透射波的形式传入箱涵内部水体,一部分以反射拉伸波的形式在箱涵顶板底面形成局部的拉应力区,如图8(b);随着时间的推移,透射波在水体中继续传播,同时,由于反射波与入射波的相互叠加,在箱涵顶部产生较大的压应力区,如图8(c)。
图9给出了箱涵内部无水条件下,爆炸冲击波的传播过程。由图8和图9对比可知,在埋深、炸药量、起爆位置等条件相同的情况下,两种工况下箱涵内的压力变化规律基本一致。但由于空气的荷载传递能力小于水的传递能力,所以通过箱涵顶板透射到内部空气中的冲击波强度非常小。
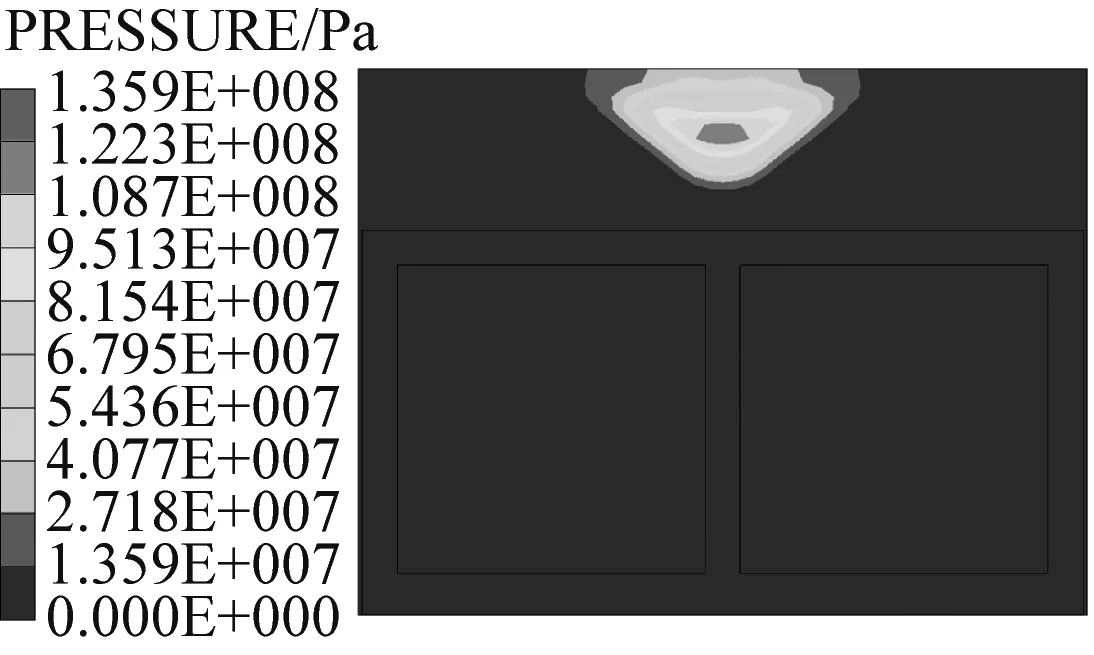
(a) t=1 ms
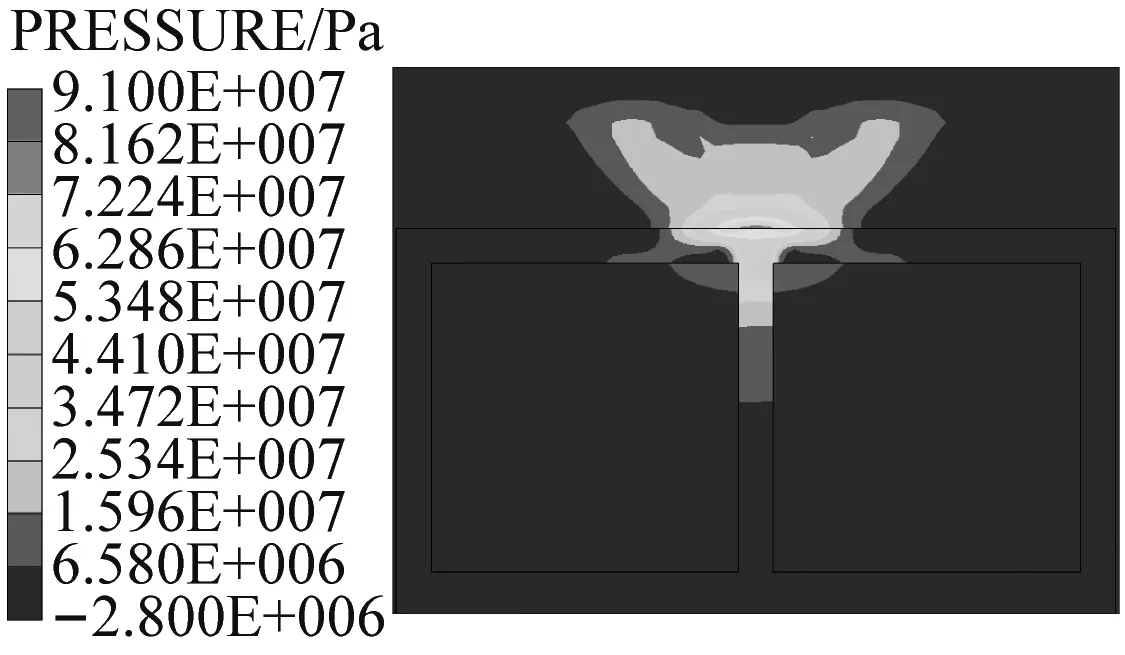
(b) t=3 ms
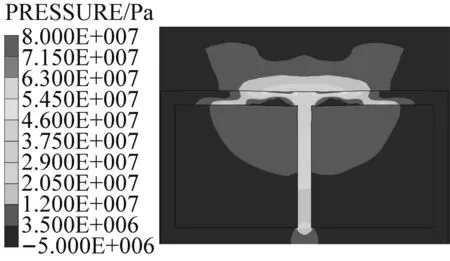
(c) t=5 ms
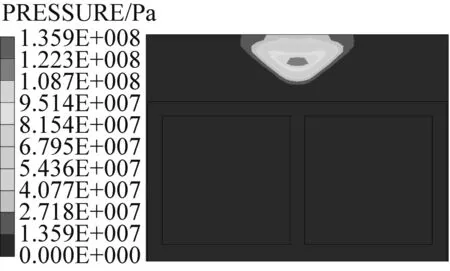
(a) t=1 ms
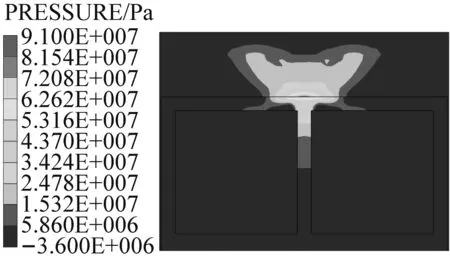
(b) t=3 ms
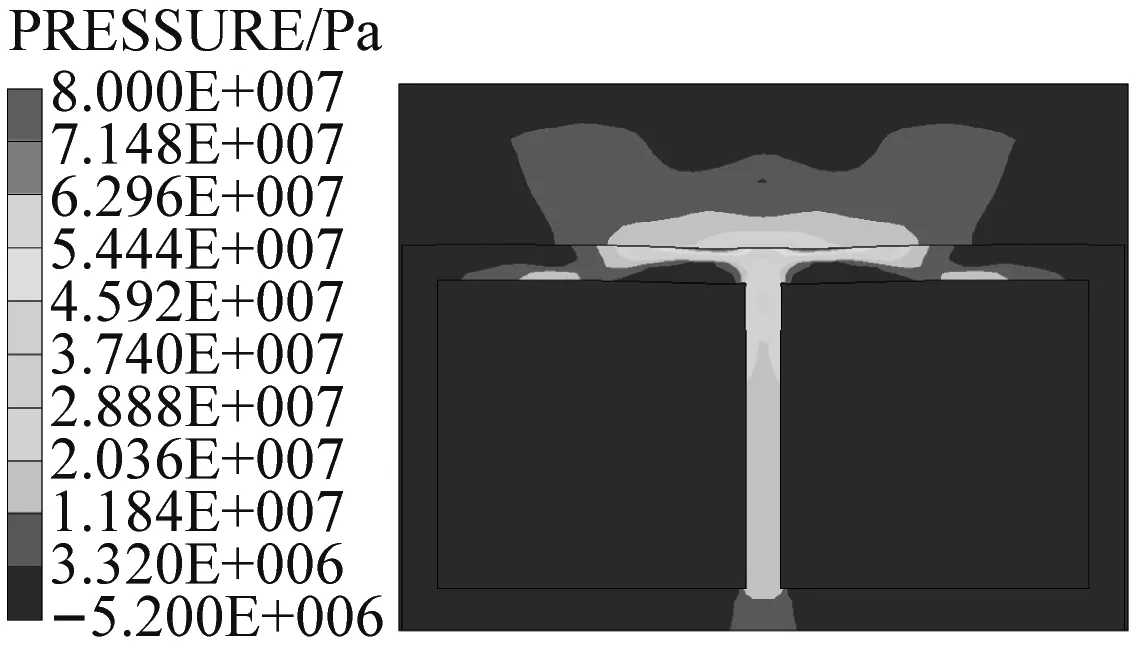
(c) t=5 ms
图10和图11分别给出了地表爆炸荷载作用下箱涵正常输水和内部无水两种工况下的损伤发展过程(损伤值0~1代表混凝土箱涵从未损伤到完全破坏)。在箱涵正常输水工况下,炸药起爆约3 ms后,冲击波传至箱涵顶板下表面,由于水的波阻抗小于混凝土材料的波阻抗,压缩波反射形成拉伸波,而混凝土材料具有低抗拉强度的特性,故在箱涵顶板的底面首先出现受拉损伤区,如图10(a)。随着时间的推移,顶板的损伤区逐渐扩大,同时箱涵的中墙上部出现一定面积的压碎区(图(10(b)~10(d))。在箱涵内部无水的工况下,箱涵的损伤发展过程与有水工况下的损伤发展过程相似。由于无水工况下箱涵顶板所受的弯矩更大,入射波在顶板底面反射产生的拉伸波也较正常输水工况下大,所以无水条件下顶板下表面及中墙的破坏更严重(图11(d))。冲击波透射到水中后还将继续传播,所以在正常输水工况下,箱涵底板与边墙的交界处出现了局部的受拉损伤区,如图10(c)、(d)。
为了进一步研究爆炸荷载作用下箱涵的动力响应特性,图12给出了箱涵对称面上顶板及边墙的三个测点的位移随时间变化过程,测点布置见图4(b)。从图12可以看出,正常输水和无水两种工况下,相同测点的位移变化规律基本相同;正常输水工况下箱涵顶板的Y方向变形小于无水工况下的变形;由于水的传递荷载能力较好,正常输水工况下爆炸荷载引起边墙X方向的变形要大于无水工况下引起的边墙的变形。输水工况下,爆炸荷载引起测点1的Y方向最大位移值约为45 mm,无水工况下,引起测点1的最大位移值约为66 mm,由于中墙的约束,测点1的位移达到最大值后有明显的回弹(图12(a));输水工况下地表爆炸引起箱涵顶板跨中(测点2)Y方向的最大位移值约为24 mm,无水工况下测点2在的最大位移值约为38 mm(图12(b));正常运行条件下地表爆炸引起箱涵边墙(测点3)X方向的最大位移值约为9 mm,无水条件下测点3在X方向的最大位移值约为2 mm(图12(c))。由图12可以看出,水体能缓冲爆炸冲击荷载对混凝土箱涵顶板的作用,改善箱涵的顶板受力,同时,水体荷载传递作用使得箱涵边墙的动力响应增大。结合箱涵损伤分布可以看出,水体的存在使箱涵整体的动力响应和损伤分布趋于均匀,有利于箱涵的整体安全。
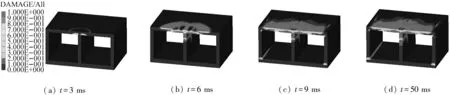
图10 过水条件下钢筋混凝土箱涵的损伤发展过程

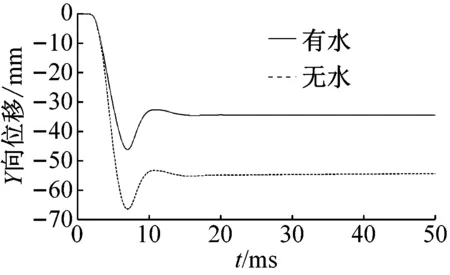
(a) 测点1
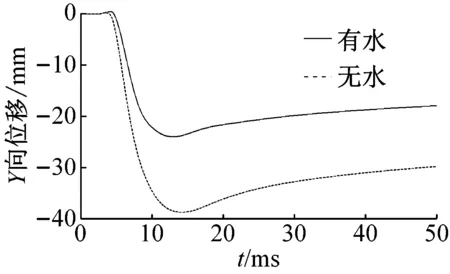
(b) 测点2
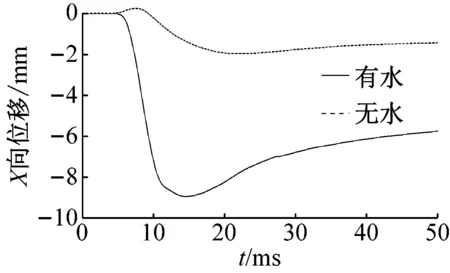
(c) 测点3
图13给出了时间为50 ms时,有水和无水两种工况下钢筋的塑性应变分布图。两种工况下钢筋的塑性应变分布规律非常相似,主要集中在中墙上部以及靠近中墙的顶板下层钢筋。无水条件下钢筋塑性区的分布范围(图13(b))要大于过水条件下的分布范围(图13(a))。但两种工况下钢筋均为发生断裂,说明箱涵结构不会发生整体性的垮塌。

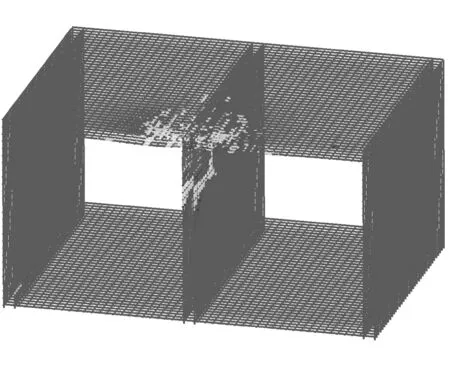
(a) 过水条件下钢筋应变分布图
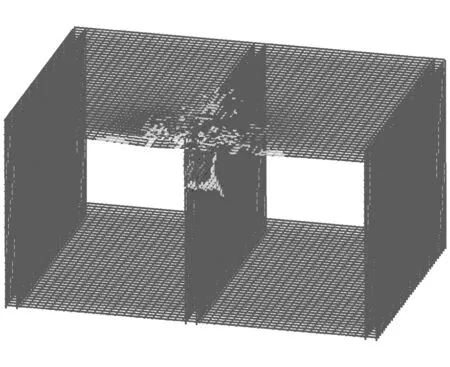
(b) 无水条件下钢筋应变分布图
4 防护措施
从上文的分析可以看出,尽管正常输水条件下箱涵结构的动态响应及毁伤程度较无水工况下小,但地表爆炸荷载作用下箱涵结构的安全仍面临着巨大的威胁,因此有必要采取一定的防护措施提高其抗爆性能。EPS(聚苯乙烯泡沫)由于其经济、便于施工等优点,工程中常被用来调整高填土下涵洞纵横向土压力分布,降低涵洞周围土压力,改善涵洞的受力状态[19]。因此,本文选取工程中最常用的EPS(聚苯乙烯泡沫)作为钢筋混凝土箱涵的防护材料,在箱涵顶部铺设0.5 m厚的EPS板,研究正常输水工况下,钢筋混凝土箱涵的动力响应及毁伤特征,如图14。空气、炸药、土体、水和EPS采用Eulerian网格,混凝土采用Lagrangian算法,钢筋采用Beam单元。网格的尺寸、模型的边界条件、箱涵埋深、炸药量以及起爆位置等均与3.1节描述相同。
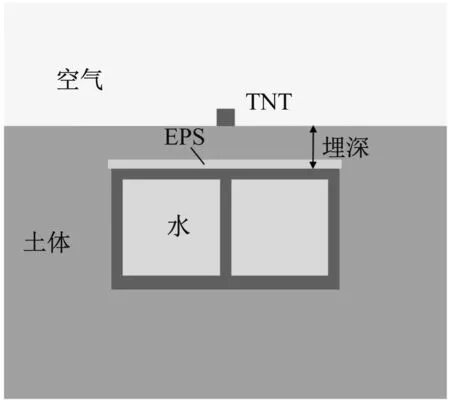
图14 考虑防护措施有限元计算模型
图15给出了有无防护措施条件下,测点1处混凝土材料的压力随时间变化过程。采用EPS防护后,作用在箱涵顶面的峰值压力明显减小。无防护措施条件下,作用在箱涵顶面的最大峰值压力约为52 MPa;采用EPS防护后,作用在顶面的峰值压力下降至43 MPa,峰值荷载减小约20%。
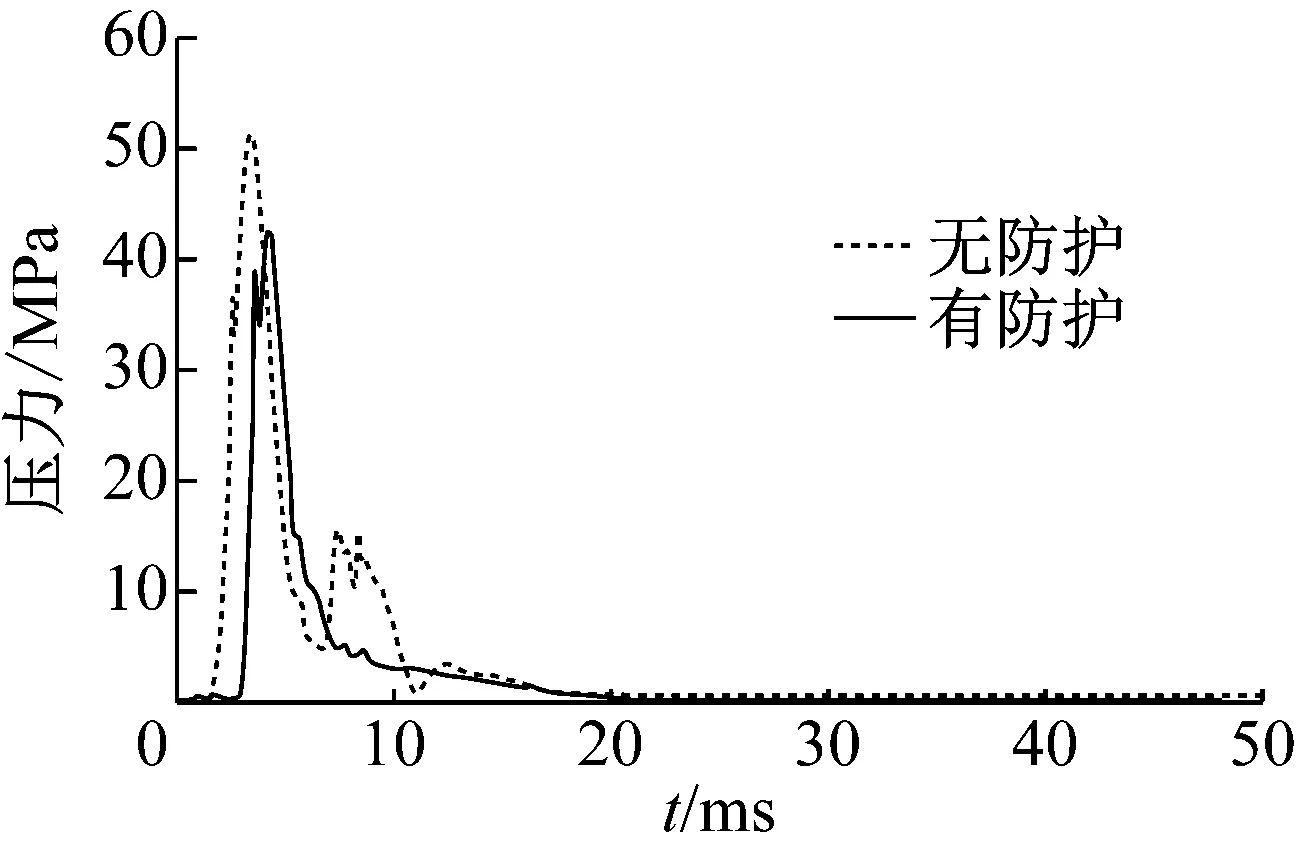
图15 1号测点压力随时间变化图
图16为测点1处顶板上层钢筋的应变随时间变化过程。采用EPS防护后,钢筋的最大应变和残余应变均有明显的减小。无防护措施条件下,钢筋的最大应变约为0.008,残余应变约为0.005;而采用EPS防护后,钢筋的最大应变和残余应变分别下降了50%和65%。说明采用EPS板能够减小作用在箱涵顶面的冲击荷载,吸收爆炸冲击波的能量,对钢筋混凝土输水箱涵具有一定的保护作用。
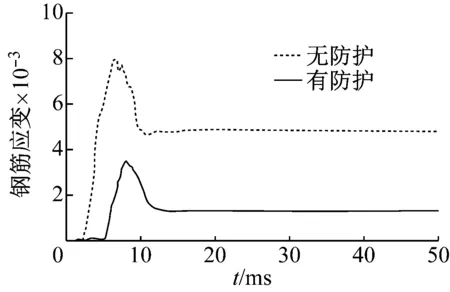
图16 钢筋应变随时间变化图
图17为正常输水条件下,不采取防护措施和采用EPS防护后钢筋混凝土箱涵的损伤分布对比图。从图中可以看出,采取EPS防护后,箱涵顶板和中墙的损伤区面积大大减小,损伤程度明显降低。当不采取防护措施时,箱涵顶板沿横向的最大破碎区长度约为5.0 m,而采取防护措施后,破碎区的长度约为3.8 m,减小了约25%;无防护措施情况下,中墙压碎区的长度约为0.9 m,采取防护措施后,中墙压碎区的长度缩小至0.4 m,减小约55%。同时,由于EPS能够吸收爆炸冲击波的能量,缓冲冲击荷载对顶板的作用,使得传至箱涵内部水体的冲击波强度减小,从而避免了边墙与底板交界处混凝土受拉损伤区的出现。
为了进一步研究EPS对提高箱涵抗爆性能的效果,图18给出了箱涵正常运行工况下,无防护措施和采用EPS防护后顶板质点Y方向最大位移沿箱涵轴向和横向的变化规律(如图18(a))。由图12可以看出,采用EPS防护后,箱涵顶板的变形较无防护措施条件下明显减小。由图18(b)可以看出,箱涵跨中Y方向位移的最大值出现在箱涵的对称面上,且随着距对称面距离的增加而减小;无防护措施下箱涵跨中顶板Y方向的最大位移值约为24 mm,采用EPS作为防护材料之后,跨中顶板最大位移值降至9 mm左右,比无防护措施下减少约60%。由图18(c)可以看出,两种情况下,质点Y方向最大位移值基本上随着距箱涵中墙距离的增大而减小,但由于中墙的约束作用,在中墙附近顶板Y方向最大位移值有所减小;箱涵顶板Y方向最大位移出现在距中墙轴线约1 m的位置,无防护措施下箱涵顶板Y向最大位移值约为70 mm,而采用EPS防护之后,箱涵顶板最大位移值降为45 mm左右,比无防护措施下减小了近35%。由图17、18可以看出,在箱涵顶部铺设一定厚度的EPS可以有效地降低爆炸荷载作用下箱涵的动力响应,提高箱涵的整体抗爆性能。

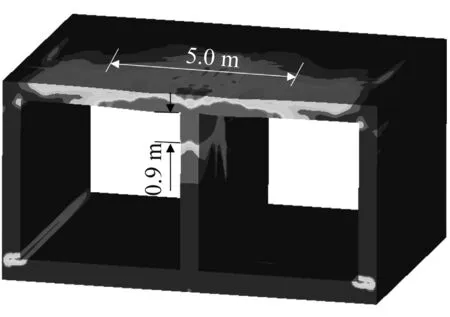
(a) 箱涵损伤分布(无防护措施)
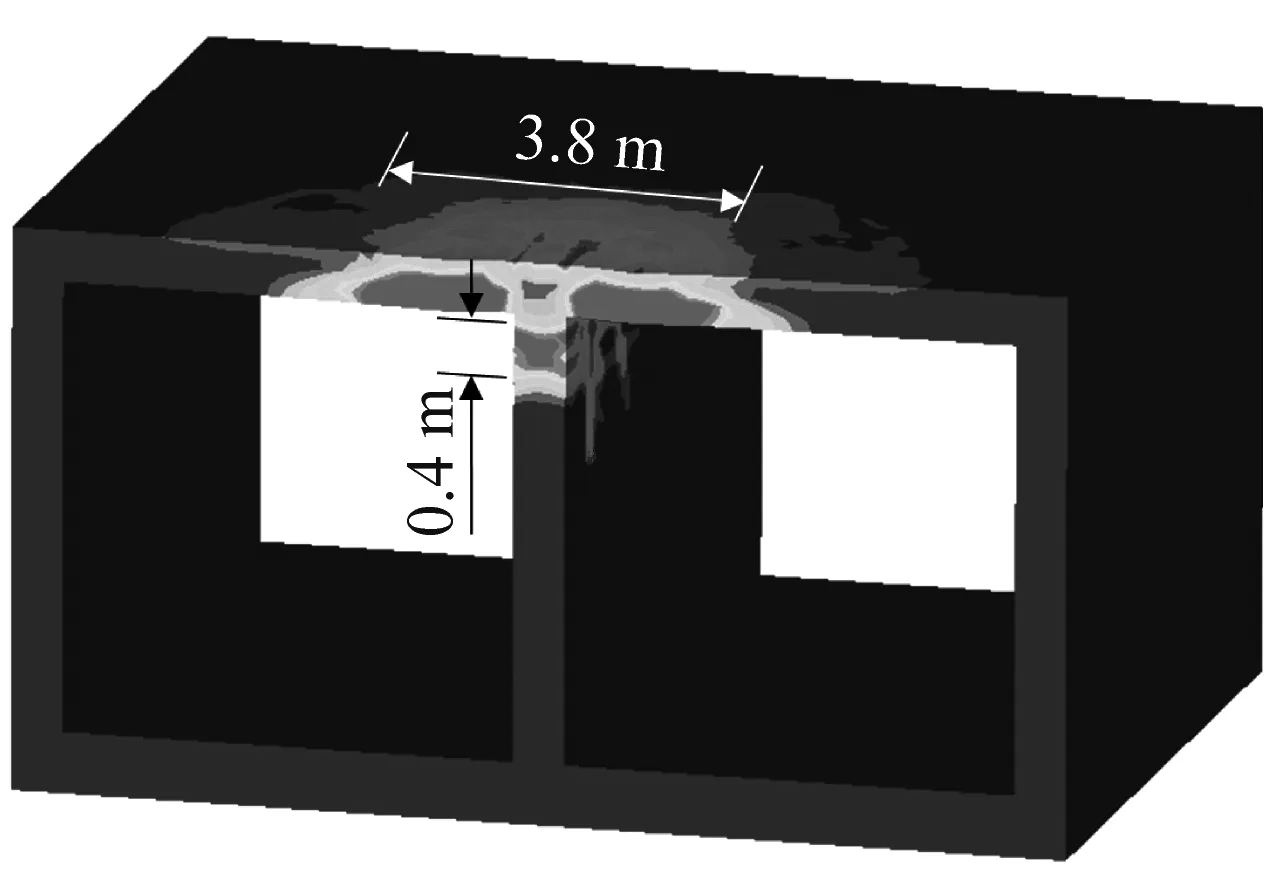
(b) 箱涵损伤分布(有防护措施)
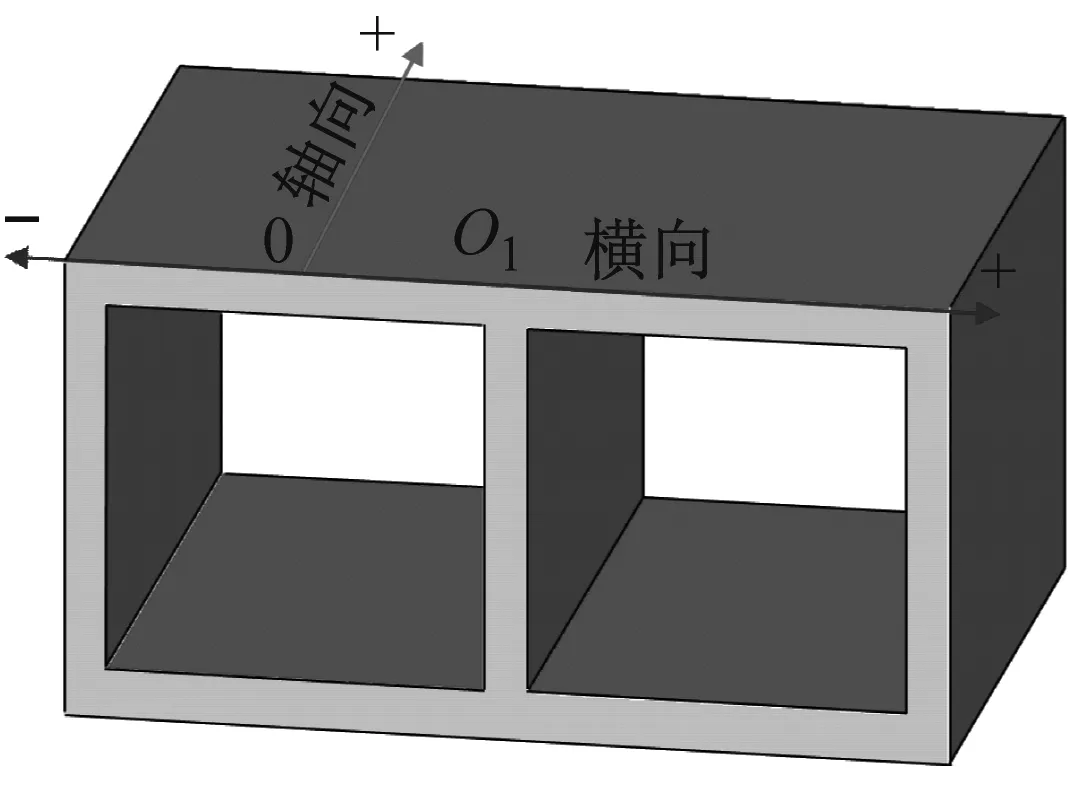
(a) 质点方向布置图
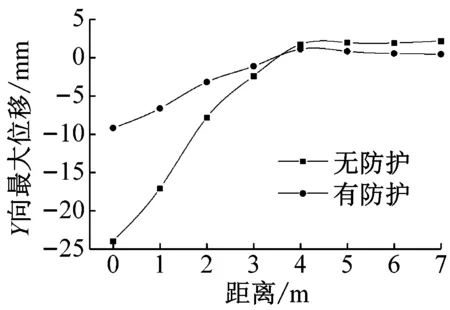
(b) 质点Y向最大位移沿轴向变化规律
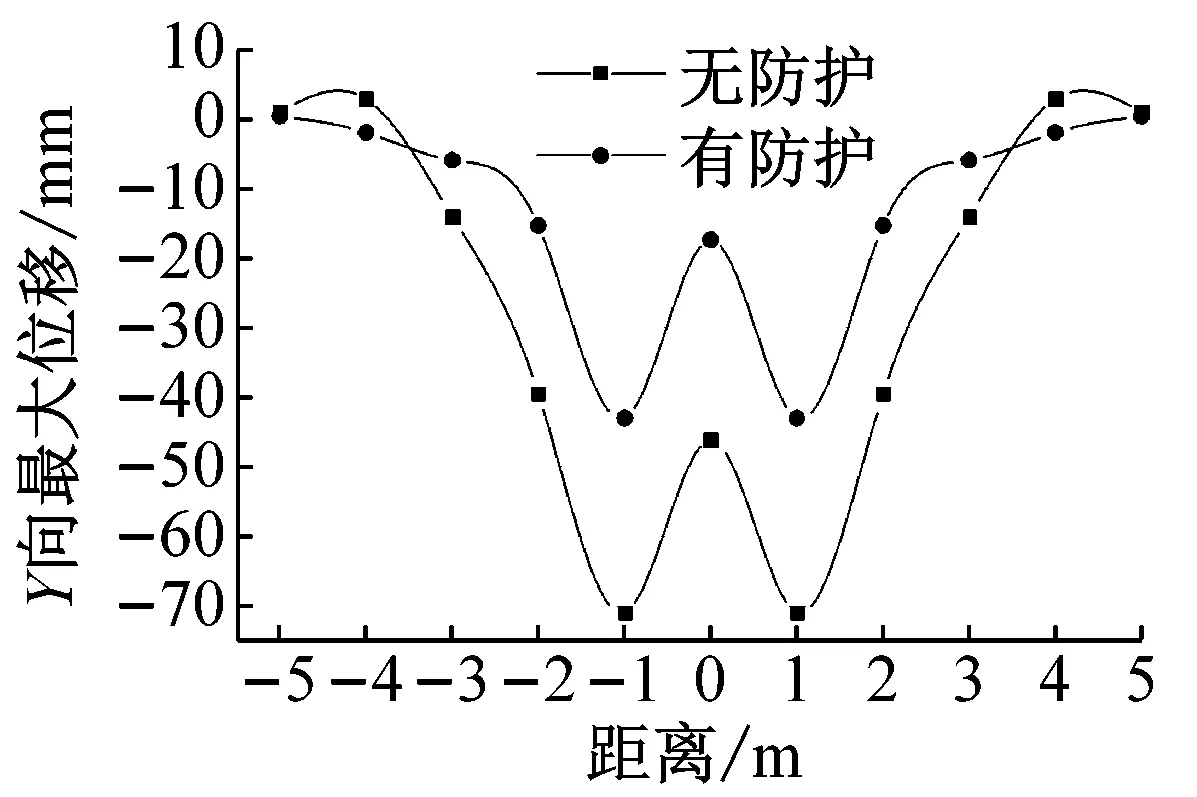
(c) 质点Y向最大位移沿横向变化规律
5 结 论
本文通过建立炸药、空气、土体、水和钢筋混凝土箱涵的全耦合模型,对比分析了箱涵内部有水和无水两种工况下箱涵的动力响应及损伤发展特征,同时提出了在箱涵顶部铺设一定厚度的EPS(聚苯乙烯泡沫)作为箱涵的防护措施,研究了其对提高混凝土箱涵抗爆性能的效果。主要得出以下结论:
(1)采用本文的土体模型及材料参数计算的土中压力峰值随深度的变化规律与经验公式(TM-5-855-1)计算的结果较为接近,说明采用本文的土体计算模型可以较好地模拟地表爆炸荷载作用下冲击波在土中的传播特性;
(2)数值模拟钢筋混凝土板的损伤分布与现场爆炸试验结果吻合地很好,说明本文的混凝土本构模型及参数能够有效地模拟爆炸冲击荷载作用下钢筋混凝土结构的损伤发展过程;
(3)地表爆炸荷载作用将使箱涵的顶板及边墙产生严重的损伤,对箱涵的正常运行构成极大的威胁;
(4)对于炸药量、起爆位置、箱涵埋深等条件相同的情况下,箱涵内部无水工况下,爆炸冲击荷载对箱涵造成的毁伤程度较正常运行工况下更为严重。箱涵正常输水条件下,水体弱化了冲击荷载对箱涵顶板的作用,改善了箱涵顶板的受力条件,使箱涵的整体变形和损伤分布趋向均匀,有利于箱涵的整体安全;
(5)在箱涵顶部铺设一定厚度的柔性防护材料(聚苯乙烯泡沫)可以有效地吸收爆炸冲击波的能量,弱化传至箱涵顶板的冲击荷载,从而提高钢筋混凝土箱涵的抗爆性能。

