基于结构动力学修改技术的传递路径分析方法
徐 铁, 王增伟, 廖 毅, 陈丹华 , 覃智威, 朱 平
(1.上汽通用五菱汽车股份有限公司,广西 柳州 545007;2.上海交通大学 机械与动力工程学院 上海市复杂薄板结构数字化制造重点实验室,上海 200240;3.上海交通大学 机械与动力工程学院 机械系统与振动国家重点实验室,上海 200240)
传递路径分析方法(TPA)广泛用于分析和处理复杂机械系统的振动与噪声问题,已被大量实验证明是一种行之有效的方法[1]。通过TPA能够识别和量化激励源,分析能量从激励源传递至目标点的路径,准确评估和排序不同传递路径对目标点的贡献量,通过控制和改进这些路径可以使噪声和振动控制在预定的目标值内。
自“源-路径-接受体”模型提出来以后,传递路径分析方法得到了很大的发展。目前,TPA家族主要包括传统TPA[2]、工况TPA(OPA)[3-5]、OPAX[6]、基于部件的TPA(Component-based TPA)[7-9]和全局直接传递率方法(Global Transfer Direct Transfer Method,也称为Advanced TPA)[10-12]等。传统TPA作为最早提出的TPA,具有精度高、方法成熟和信息丰富的优点,已成为处理汽车NVH问题的标准TPA[13],但由于需要对主动部件解耦,其测试过程复杂,分析效率较低。
为了提高TPA的分析效率,基于传递率矩阵的工况TPA得到了快速的发展。传递率矩阵表征“响应-响应”关系,其本质上是对传统TPA中“力-响应”关系的近似[14],因此,尽管工况TPA分析效率较高,其存在路径串扰、传递率矩阵病态以及路径遗漏导致的计算错误问题。OPAX在传统TPA理论的基础上,采用参数化模型对耦合界面载荷进行识别,降低了对测试数据量的要求,在一定程度上提高了传统TPA的分析效率,但由于仍然需要拆分系统,其测试过程比较复杂,效率较低。近年来,国内外学者提出了更多的新型TPA,如基于部件的TPA和全局直接传递率矩阵方法。在理论上,基于部件的TPA可以通过系统级的频响函数与工况响应就可以得到与传统TPA一样的分析结果,但其在计算阻抗力或自由速度的过程中,需要测试与耦合界面所有自由度相关的系统级频响函数(包括与转动自由度相关的频响函数),测试过程复杂,计算精度难以保证[15]。全局直接传递率矩阵方法是一种相对路径分析方法,其方法原理与其他TPA方法不同,其计算结果被称为相对路径贡献度,该方法可以视为以传统TPA为代表的绝对路径贡献度计算方法的重要补充[16]。后续发展的TPA虽然可以缩短实验时间,但是常以牺牲精度为代价[17]。
结构动力学修改是用于结构振动特性问题的高效重分析和重设计技术[18]。通过结构动力学修改技术,可以正向预估局部修改效果[19],也可以逆向确定降低振动响应的结构局部修改方案[20]。其正向预估结构修改效果也被称为虚拟修改预测,通过虚拟修改模拟系统的虚拟工况,建立系统的被动件频响函数与虚拟系统响应之间的关系,进而识别被动件的频响函数,能够在保留了传统TPA优点的同时,有效地提高传统TPA的分析效率。
目前,国内外对结构动力学修改技术的研究主集于新系统模态参数和频响函数的预测,很少涉及新系统工况响应的预测。本文首先简要介绍结构动力学修改工况响应预测理论,在此基础上,提出一种基于原位测量频响函数的传递路径分析方法。该方法通过耦合系统频响函数预测子结构频响函数,同时识别耦合点连接动刚度,计算响应传递路径贡献度。在数值案例验证该方法有效性的基础上,进行车身振动传递路径分析应用研究,验证该方法的工程可行性。
1 基于结构动力学修改技术传递路径分析方法
1.1 结构动力学修改工况响应预测理论
结构动力学修改工况响应预测方法采用原系统的响应和频响函数预测结构局部修改后的系统工况响应。一般复杂机械系统可以划分为几个独立的部件,每个部件都用频响函数表征其动态特性,部件之间通过各种弹性和阻尼元件联结来传递信息。图1为主动部件和被动部件组成的复杂系统的示意图,两个部件通过弹性元件相连接,主动部件受到激励作用。为了方便推导公式,将图1中的系统离散化成m自由度的系统,如图2所示。
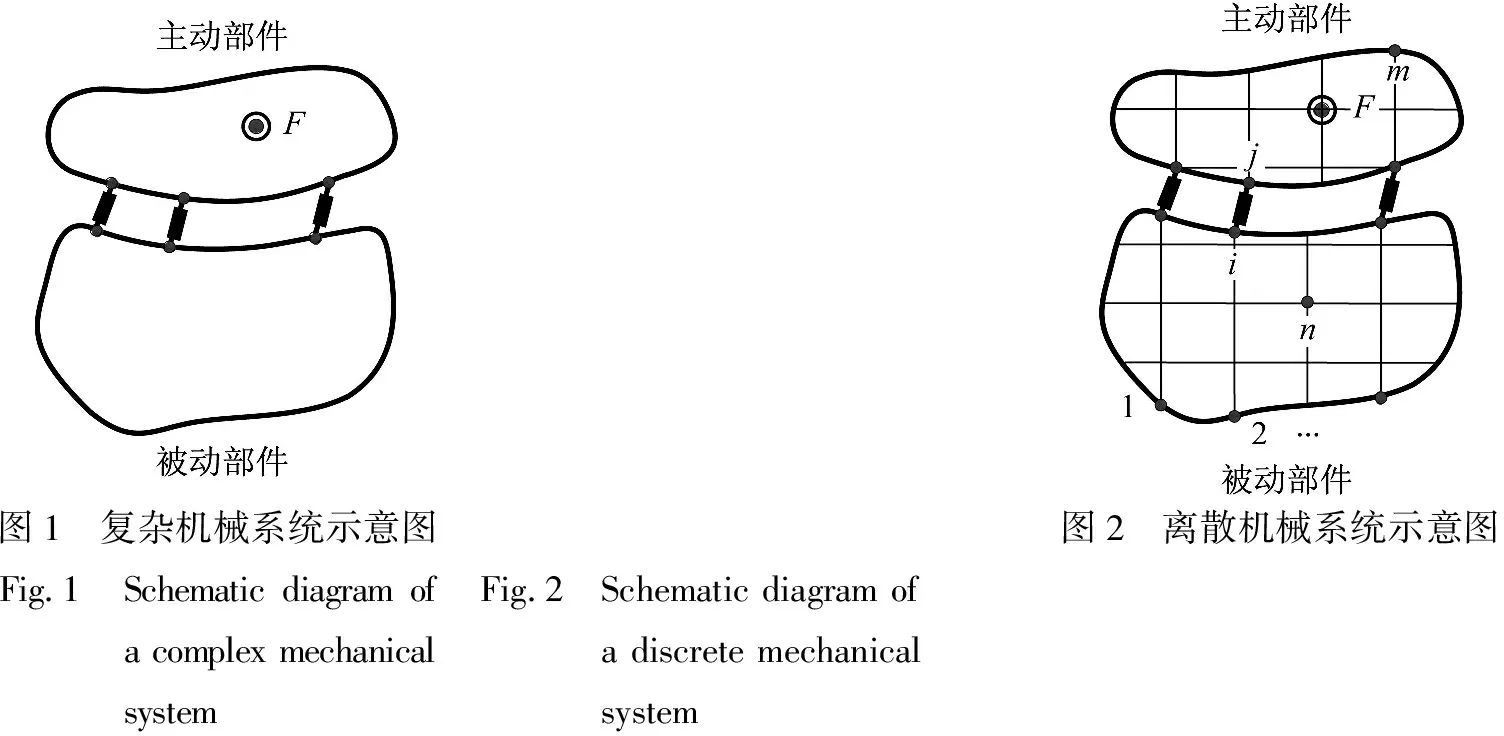
图1 复杂机械系统示意图Fig.1 Schematic diagram of a complex mechanical system图2 离散机械系统示意图Fig.2 Schematic diagram of a discrete mechanical system
该系统的动力学方程则可以表示为
X(ω)=H(ω)F(ω)
(1)
式中,X(ω)是系统响应向量,F(ω)是系统所受载荷向量,H(ω)是系统频响函数矩阵。为了简便,在下文公式推导中省略角频率ω。若前n个自由度是需要关注的(重要自由度),记为1,2,3…i,j…n,这些自由度代表需要局部修改的结构点。系统中的其他自由度则可记为n+1,…,m。根据集总参数模型和有限元理论,系统频响函数矩阵可以表示为
(2)
式中,Hit是重要自由度的频响函数矩阵,Hun是剩下自由度的频响函数矩阵,Hit,un/Hun,it是两组自由度之间的频响函数矩阵。它们可以表示为
(3)
(4)
(5)
(6)
系统的动刚度矩阵是频响函数矩阵的逆矩阵,即
(7)
假设系统所受到的载荷保持不变(高导纳特性振源假设),则结构修改后重要自由度动刚度矩阵变为
(8)
新系统的动力学方程为
(9)
经推导,重要自由度的响应表达式为
(10)
式(10)是结构动力学修改工况响应预测方法的核心公式,详细的推导过程可见参考文献[20]。对于用动刚度表征的结构修改,根据式(10),可以通过原系统重要自由度的频响函数和响应计算得到新系统重要自由度的响应。
为了建立被动件频响函数与新系统响应之间的关系,进而识别出被动件的频响函数,将图2中的自由度i变为与地弹性连接,即如图3所示,连接动刚度为Kig,则重要自由度动刚度矩阵改变部分为
(11)
将自由度i连接地本质上是对自由度i施加一个额外力,该力的大小为连接刚度Kig和自由度i响应的乘积,即
(12)
对于一个假设的连接刚度值Kig,可以通过公式(10)计算得到自由度i的响应,进而通过公式(12)计算得到该连接对系统的作用力。因此,在结构动力学修改工况响应预测理论框架内,将自由度连接地实质上是对系统施加虚拟作用力来改变系统响应。
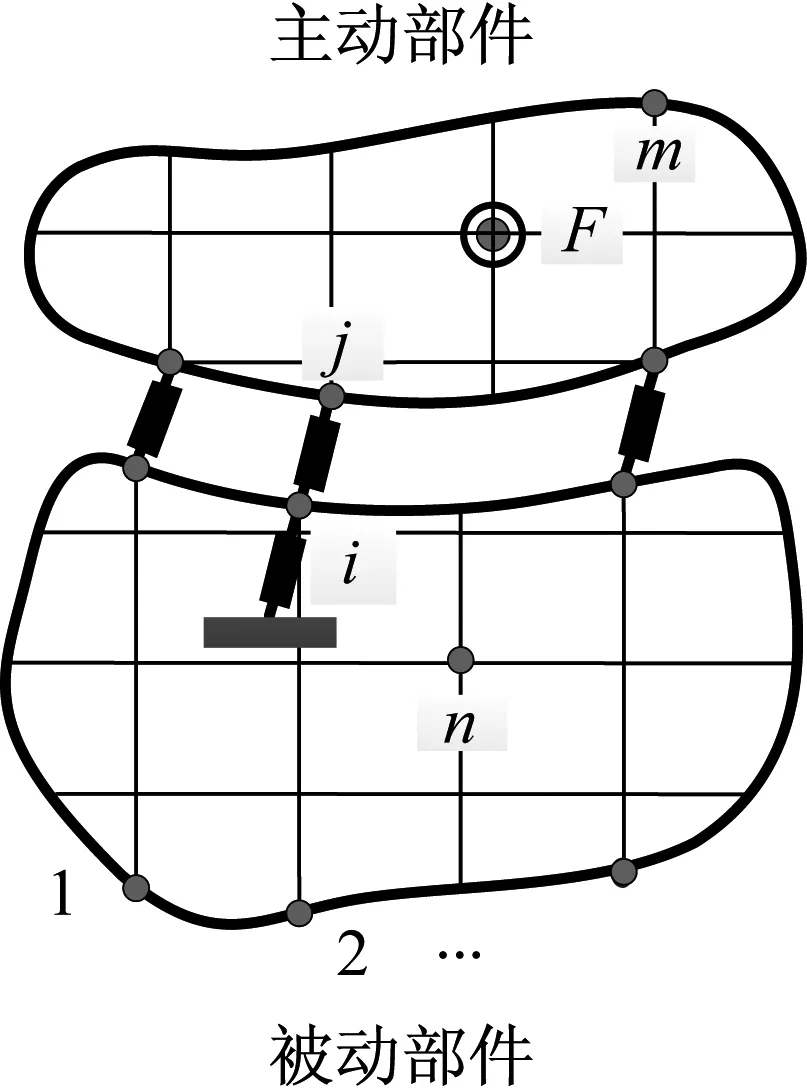
图3 与地连接的机械系统
1.2 基于结构动力学修改技术的传递路径分析流程
在传统TPA中,目标位置的响应被认为是不同传递路径贡献度的线性和,每个传递路径贡献度是该路径的耦合力与频响函数的乘积。因此,目标响应可以表示为
Xt=HdFc
(13)
式中,Xt是目标位置的响应向量,Hd为被动件上耦合点到目标位置的频响函数矩阵,Fc为耦合力向量。可知,传递路径分析方法需要测量频响函数和耦合力,在测量频响函数时,需要拆掉主动部件,这使得TPA实施过程繁杂,周期较长。为了提高TPA的分析效率,降低TPA的实施难度,采用结构动力学响应预测方法进行耦合系统的虚拟解耦,在不拆分系统的情况下预测被动部件频响函数和耦合力。
当耦合点被动件一侧的i点变为与地弹性连接,目标位置的响应和耦合力都会发生改变,且目标响应为耦合力和虚拟力共同作用的结果,即
(14)
Hd,ti为被动件上耦合点i到目标响应的频响函数向量。此外,耦合力也可以表示为耦合点响应差值与连接动刚度的乘积
(15)
式中,Ki为连接动刚度。式(14)可重写为
(16)
式中,Kc为对角矩阵,对角元素为耦合点连接动刚度。
假设有s个耦合连接且目标点为自由度n,可知式(14)中共有s+1个未知量,即s个Hd,niKi和一个Hd,ni。当耦合点主动件一侧的j点变为与地弹性连接,目标位置的响应和耦合力也发生改变,但目标响应是耦合力作用的结果,即
(17)
可知式(17)中有s个未知量,即s个Hd,niKi。
联立式(14)和式(17),可得
(18)
为了消去式(18)中的矩阵奇异性,至少还需要s-1组不相关数据,可以通过将余下s-1个耦合点主动侧自由度依次与地虚拟连接得到。本质上,这相当于在主动部件上施加s个不相关的虚拟作用力。通过耦合点主动侧的s组数据和被动侧的1组数据,采用H1估计方法求解Hd,ti
(19)
“+”表示虚逆操作。
以此类推,将其他被动侧耦合点与地连接,则可以得到被动件上耦合点到目标点的频响函数矩阵Hd,同时也可以得到连接动刚度矩阵Kc。将计算得到的被动件频响函数和连接动刚度代入式(13)则可以进行贡献量分析。
采用结构动力学修改响应预测方法进行传递路径分析,只需要系统的频响函数和1组实际工况数据作为输入,其预测虚拟工况响应,对系统进行虚拟解耦,避免实际拆分系统。
2 数值案例研究
选取9自由度质量-弹簧-阻尼系统校验所提方法的有效性。模型如图4所示,M、K和C分别代表系统的质量、刚度和阻尼,具体参数见表1。系统由一个主动件和一个被动件组成,两个部件通过3个弹簧-阻尼元件连接,质量块1的位移为目标响应,因此,有7个需要关注的自由度。
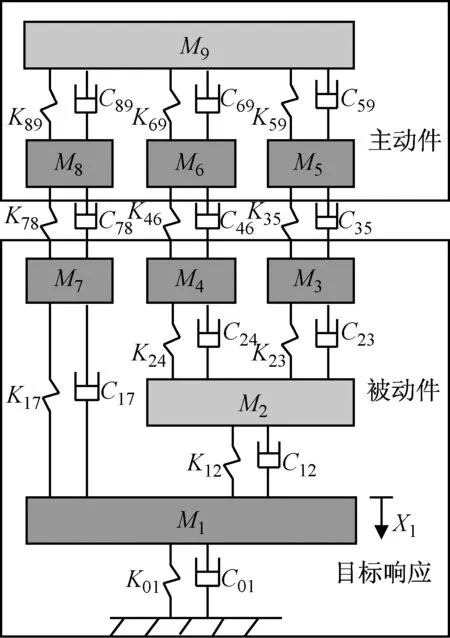
图4 9自由度离散机械系统

在质量块5、6、8和9上施加一组力模拟工况,采用结构动力学修改响应预测方法进行传递路径分析的流程如下:
(1) 系统未受工况力作用时,测量7个自由度之间的频响函数矩阵;
(2) 系统受到工况力作用时,测量7个自由度的工况响应;
(3) 采用式(10)计算耦合点被动侧与地连接、主动侧与地连接时的虚拟工况响应,通过式(19)计算被动件频响函数和耦合连接动刚度;
(4) 结合真实工况数据,采用式(13)计算路径贡献度。
部分计算结果如图5~图7所示。图5为质量块3到目标自由度的解耦频响函数,实线代表真实值,星号代表所提方法得到的结果,由图5可知,预测得到的解耦频响函数与真实值相同。此外,质量块4和7到目标点的解耦频响函数与真实值也分别相同。图6为主动件与被动件之间的工况耦合力,图7展示了3条传递路径的贡献度,将3条路径贡献度合成目标响应,并与真实值作比较,结果如图8所示,可知目标点的合成响应与真实响应完全一致。
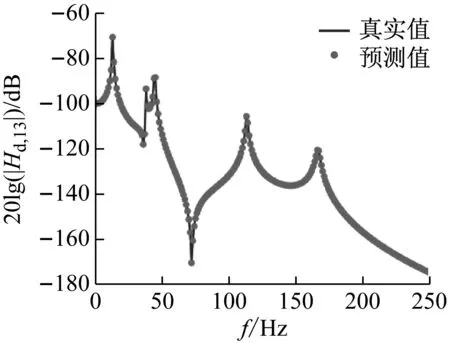
图5 质量块3到1的解耦频响函数
3 轿车车身振动传递路径分析应用研究
以某款MPV整车振动传递分析为例,验证所提方法的工程有效性和应用简便性。由于所提方法是基于传统TPA的理论框架,因此只需要验证该方法对车身解耦频响函数的预测能力。
该车动力总成通过3个橡胶悬置与车身连接,如图9所示。悬置的发动机侧分别记为a1、a2和a3,车身侧记为p1、p2和p3,选取车身底板某处安装硬点垂向加速度为目标响应,记为t(如图10所示)。悬置布置示意图及全局坐标系如图11所示。通常只考虑悬置点的平动自由度,因此有19个重要自由度。
采用锤击法测量耦合车身的频响函数,为了方便使用力锤和粘贴加速度传感器,在悬置两端处安装特制的装置。在悬置点用3D加速度传感器拾取加速度信号,在目标点采用1D加速度传感器拾取加速度信号。力锤的型号为Kistler 9724A2000,3D加速度传感器型号为Kistler 8763B,1D加速度传感器型号为厚德HD-YD-213。通过LMS系统采集力锤和加速度传感器信号,采样频率为4 000 Hz,计算5次测量的平均值。分析频段为20~250 Hz,左悬置车身侧到目标点的车身耦合频响函数测试结果如图12所示。用MATLAB软件建立所提方法的程序,以所测的车身耦合频响函数作为输入,且将一个频响函数测试数据作为工况测试数据,用所提方法计算车身解耦频响函数。同时,对该轿车发动机进行拆掉,用起重机和木棒将其悬吊起来,使之与车身完全脱离,进行车身解耦频响函数测试,如图13所示。车身解耦频响函数的预测值和测量值如图14所示,图14(a)为左悬置下点X方向到目标点的解耦频响函数,图14(b)为左悬置下点Y方向到目标点的解耦频响函数,图14(c)为左悬置下点Z方向到目标点的解耦频响函数。由图可知,在20~50 Hz频率段存在较大的偏差,这是由于较低频段测试数据不精确导致的,所提方法的计算值与测量值在整体上比较吻合,这说明所提方法具有较好的预测效果,验证了该方法在实际工程应用中是可行有效的,利用得到的解耦频响函数,可以开展车身振动传递路径分析。由于所提方法不需要拆分系统,这必然会提高分析效率,降低传递路径分析方法的应用难度。
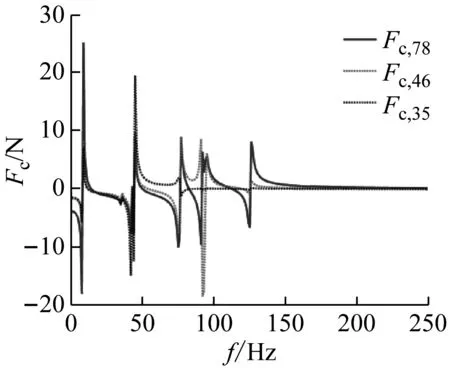
图6 工况耦合力
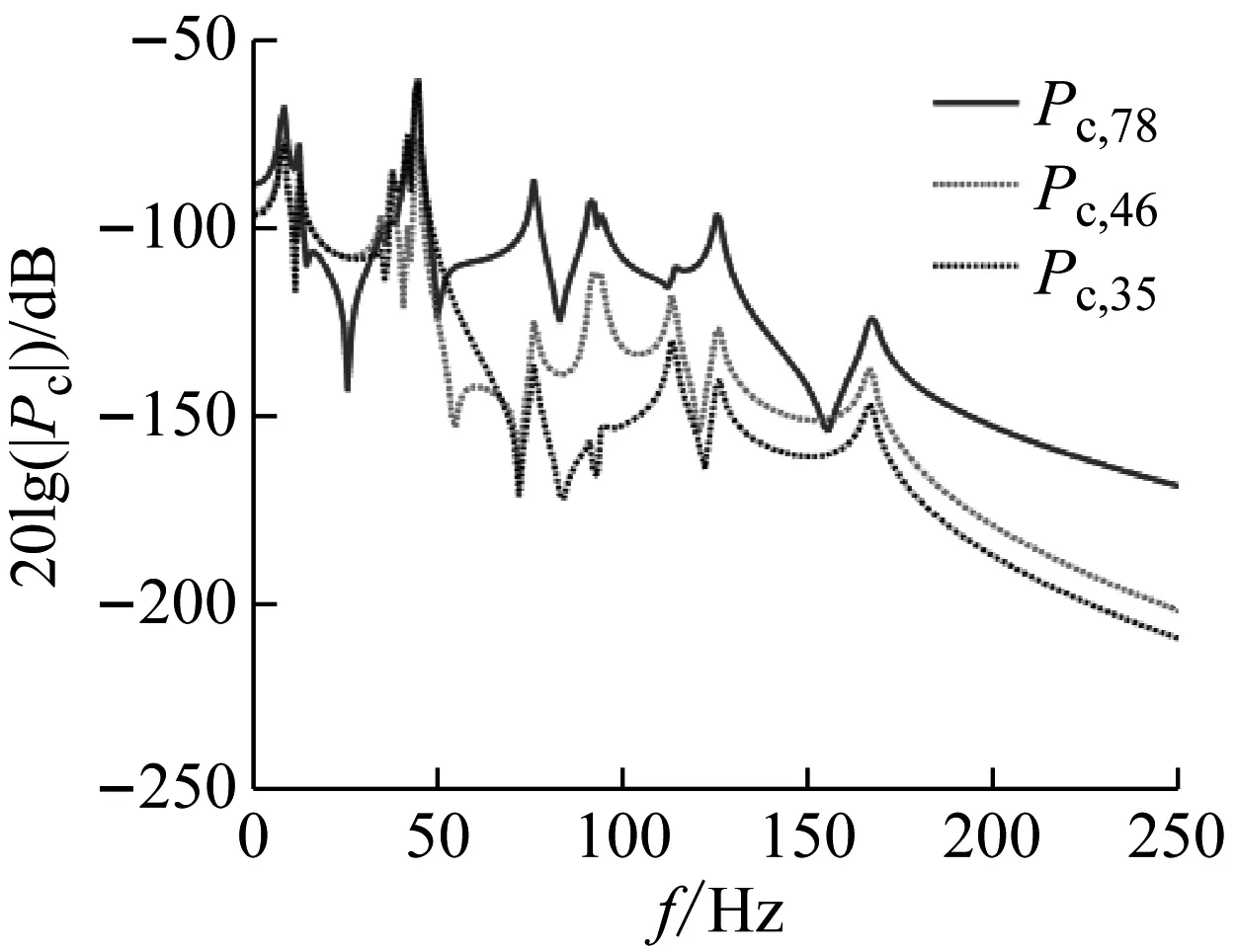
图7 传递路径贡献度
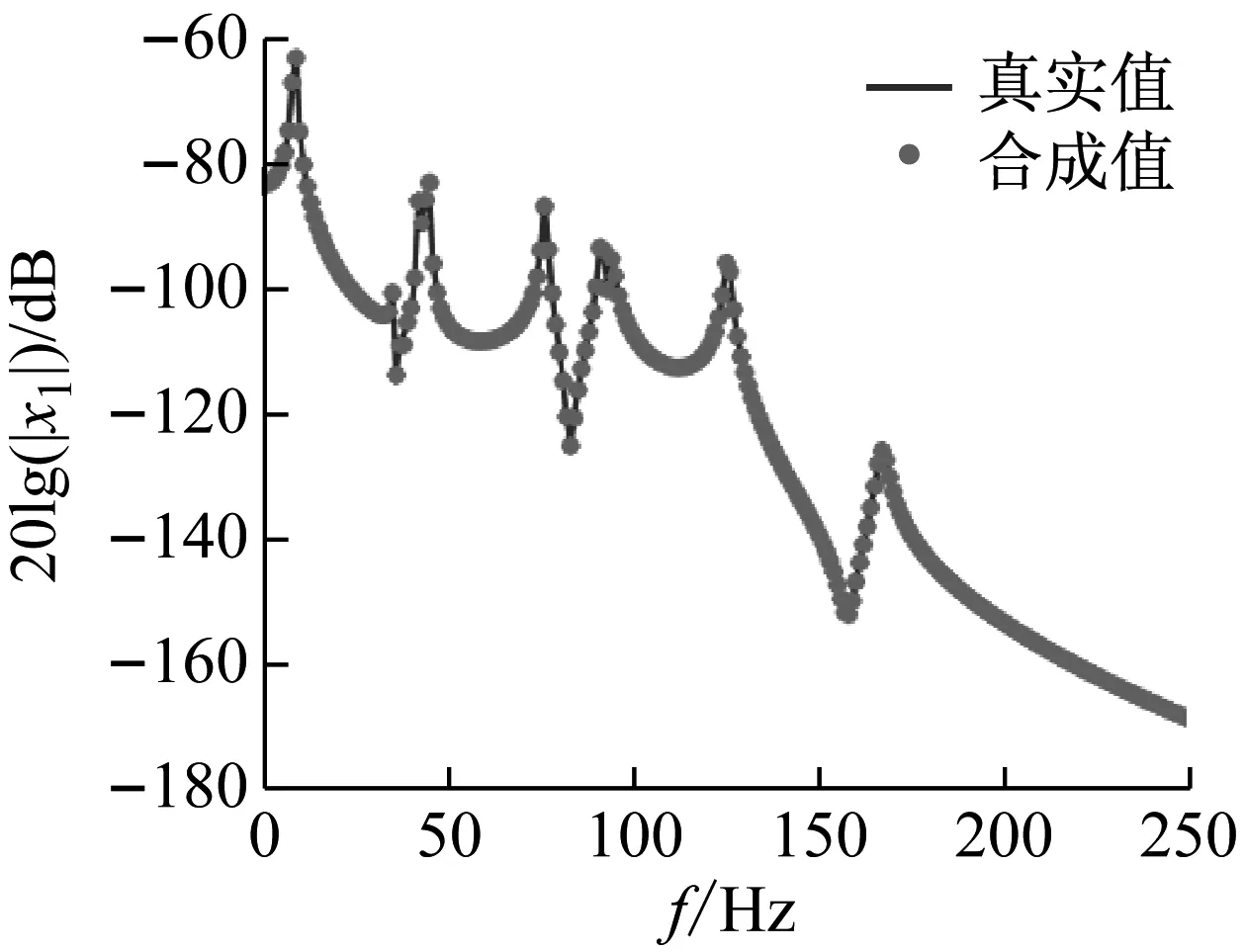
图8 目标响应

图9 车身耦合系统实验测试

图10 目标响应位置
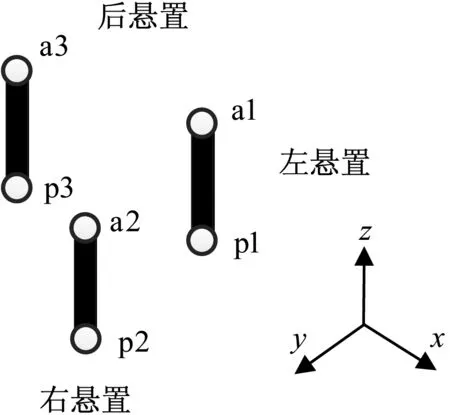
图11 悬置布置及全局坐标系
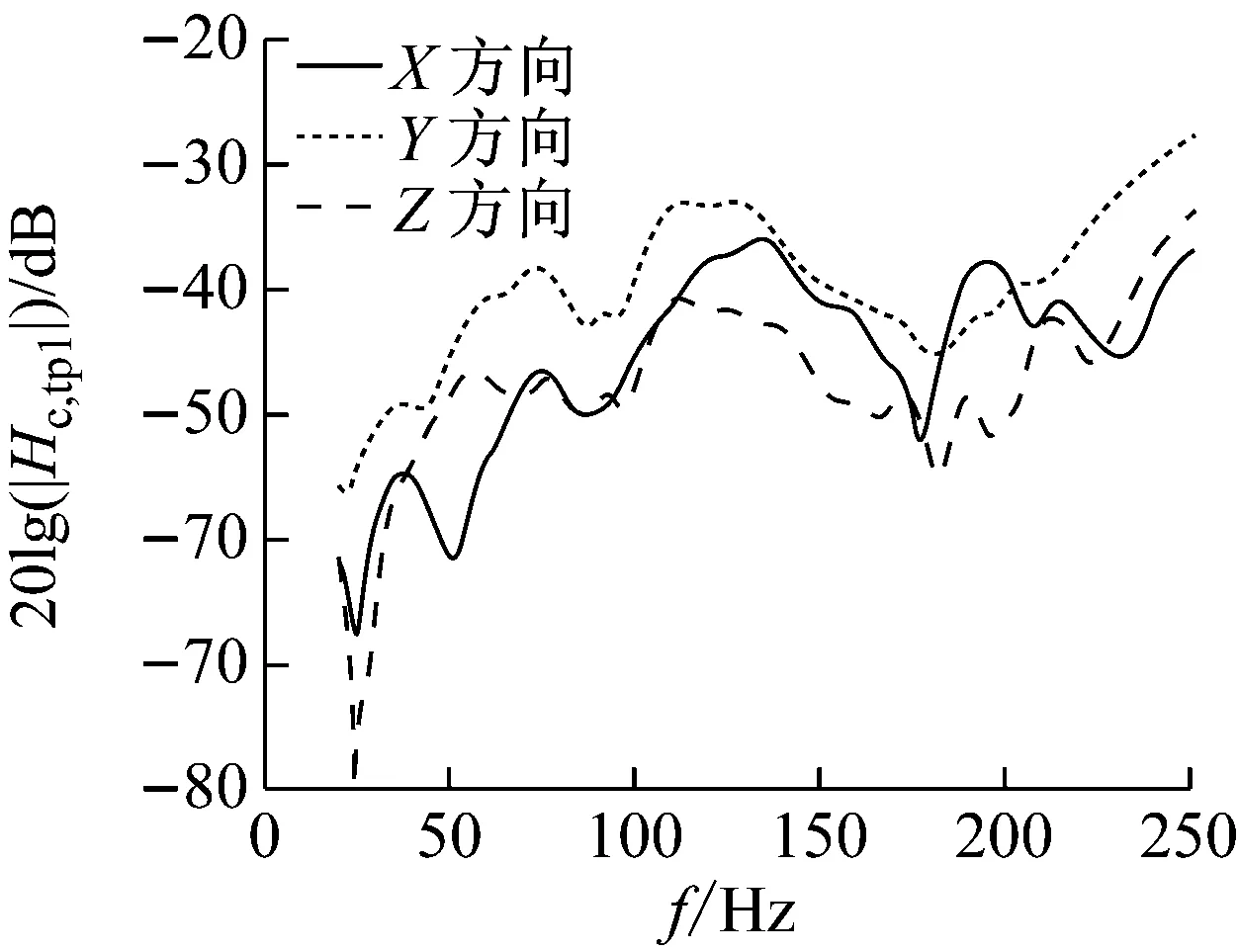
图12 左悬置车身侧到目标点的耦合系统频响函数
4 结 论
提出了一种基于结构动力学修改技术的传递路径分析方法,得到了从耦合系统频响函数和工况响应计算路径贡献度的理论公式。采用数值案例校验了所提方法的有效性,采用实车案例进行了工程可行性验证。

(a) 起重机起吊发动机

(b) 木棒支撑发动机后悬置附近位置
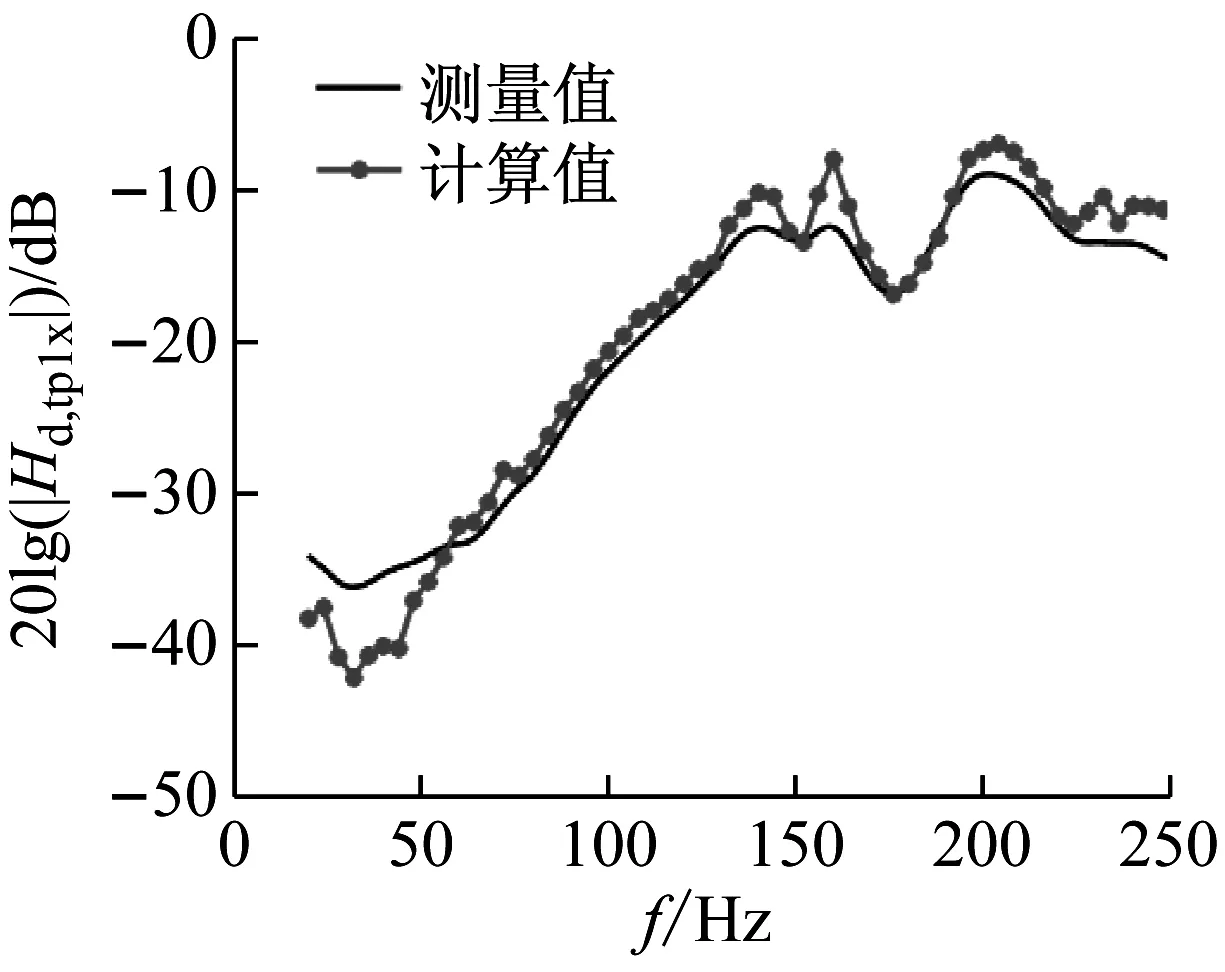
(a) p1点X方向到目标点的解耦频响函数

(b) p1点Y方向到目标点的解耦频响函数

(c) p1点Z方向到目标点的解耦频响函数
(1) 通过数值案例可以发现,所提方法根据系统的频响函数和工况响应可以准确地计算出被动件的频响函数,进而识别出工况耦合力,得到路径贡献度。
(2) 在车身振动实验分析案例中,用所提方法预测车身解耦频响函数与试验测试值相吻合,证明所提方法在工程应用中是可行有效的,为开展轿车车身NVH性能分析提供可借鉴的新方法和途径。

