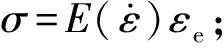一种弹芯用聚碳酸酯的动态力学性能研究及本构关系

王江波， 高光发， 杜忠华， 徐立志， 刘 鹍, 朴春华

(1. 南京理工大学 机械工程学院，南京 210094； 2. 陆军装甲兵装备技术研究所，北京 100072； 3. 黑龙江北方工具有限公司，黑龙江 牡丹江 157013)

随着现代社会科学的发展，人工合成了各种性能良好的高分子复合材料，被广泛地应用于建筑、国防工业和航空航天等领域。其中聚碳酸酯(Polycarbonate，PC)应用最为广泛。聚碳酸酯作为一种工程塑料具有以下优点：光学透明性好、玻璃化转化温度高、常温韧性好、尺寸稳定性好、吸水率低、阻燃性和电绝缘性好。在弹药毁伤领域，横向效应弹(Penetrator with Enhanced Lateral Effect，PELE)是由Paulus等[1]和Kesberg等[2]提出的一种具有横向效应的新型多功能穿甲弹，而装填物材料对PELE横向效应的影响已有许多研究。陈春晓等[3]、涂胜元等[4]、尹建平等[5]、朱建生等[6]、蒋建伟等[7]等对改性PA1010、Nylon、Rubber、聚乙烯、聚碳酸酯、聚氨酯等作为弹芯的材料进行了研究，发现填充物材料对PELE穿透主靶后形成的破片数量和毁伤面积影响很明显；惠旭龙等[8]利用电子万能试验机和高速液压伺服试验机对2A16铝合金进行常温下准静态和中应变率力学性能试验，并研究了该材料的应变率效应。

而关于聚碳酸酯力学性能方面的研究，已经有很多的可参考文献。Mulliken等[9]利用伺服液压试验机和SHPB研究了不同应变率下(10-4～104s-1)PC材料的力学性能；Richeton等[10-12]研究了温度和应变率对PC聚合物力学性能的影响，发现温度和应变率对聚碳酸酯的力学性能有很大的影响，并对原有的模型进行了改进；Senden等[13]改进了PC材料基于橡胶弹性模型的应变硬化模型，把一部分弹性应变硬化用粘性代替，并用实验进行了验证；Safari等[14]建立了PC材料在大变形和高应变率情况下的本构模型，并将之嵌入到有限元分析中，对比仿真和实验结果，验证此本构模型具有一定的准确性。Lu等[15]研究了聚合物在高应变率下的压缩动态力学行为，发现聚合物的屈服应力具有明显的应变率效应。胡文军等[16]认为PC材料动态压缩的应力应变关系与准静态实验有所差异，主要表现在应变软化现象变弱，屈服应力增大；接着胡文军等[17]又研究了应变率为3.8×10-5s-1～8.0×103s-1范围内PC材料的单轴压缩力学行为，分别得出了屈服应力与低应变率和高应变率的线性关系，并对聚碳酸酯的应变硬化与应变软化进行了分析。

关于填充物本身力学性能对PELE横向效应的影响，却缺少系统性的研究，本文基于以上的研究状况，采用材料试验机和分离式霍普金森压杆(SHPB)研究了PC材料在常温下得准静态和动态压缩力学性能，结合实验和理论分析建立了PC材料的本构模型，并与试验作对比，结果表明该模型与实验结果吻合的较好。

1 实验与材料

1.1 材料和试件

本实验使用的聚碳酸酯是某PELE的弹芯材料，密度为1.2 kg/m3，比热为1.17 J/(g·℃)。实验所用试样由聚碳酸酯(PC)棒料经过机械加工为指定尺寸。对于准静态压缩实验，根据《GB-T 7314—2005室温压缩试验方法》设计试件尺寸长度为20 mm(L)、直径为10 mm(D)、长径比为2(L/D)，如图1(a)所示，而动态冲击压缩实验的试件尺寸由唐志平[18]的研究确定，试件尺寸长度为5 mm(L)、直径为10 mm(D)、长径比为0.5(L/D)，如图1(b)所示。

1.2 压缩试验及方案

PC材料的准静态压缩试验采用电子万能试验机(10T)进行实验，如图2(a)所示，聚合物的压缩原试样如图2(b)所示，将压缩试样放置于底座与压头的正中间进行压缩试验，如图2(c)所示，在室温条件下，测试PC试件应变率为10-3s-1和10-2s-1两种，试验机的速率分别为1.2 mm/min和12 mm/min，压缩完成后的试样如图2(d)所示，聚合物每个应变率条件下至少重复三次试验，以确保试验数据的准确性，数据采集软件记录了试件原始载荷与位移的曲线，通过计算得到试件的真实应力和应变。

图1 压缩试件示意图

动态压缩试验(SHPB)采用直径为14.5 mm的SHPB装置，如图3所示，子弹、入射杆和透射杆都为钢杆，入射杆和透射杆分别轴向对称贴着两个应变片用来记录入射波、反射波和透射波，在入射杆的撞击端贴有整形片，它不仅可以减小应力脉冲过冲，而且还可以过滤掉高频应力波，减小波形震荡，还能将入射波上升沿拉长，使试验在恒应变率的条件下进行，SHPB试验系统的几何参数和物理参数如表1所示。对于试件的处理，试件的两端面必须保证平行且比较光滑，在实验时，试件的两个端面涂有润滑油(凡士林)以减小端面的摩擦。基于一维平面波理论，利用MATLAB程序，得出试件的真实应力—应变曲线。在试验过程中，试件的工程应变率可通过改变初始气压和子弹长度来控制。至少在相同条件下重复四次，以获得可靠的数据。

图2 准静态压缩试验系统

图3 SHPB试验装置

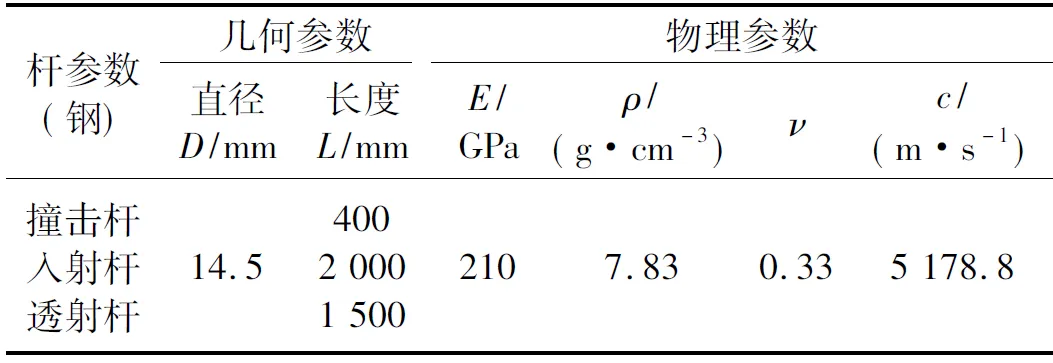
1.3 测试原理和基本方程

为了获得PC材料准静态压缩条件下的真实应力应变曲线，首先将采集到的压力-位移(F-S)曲线结合试件的初始尺寸，转变为工程应力应变曲线；然后根据材料不可压缩的假设，将工程应力应变转化为真实应力应变，两者之间的转化关系为

σT=σE(1-εE)

(1)

εT=ln(1-εE)

(2)

式中，σT为真实应力，σE为工程应力，εT为真实应变，εE为工程应变。

在SHPB实验中，当入射杆的应力波到达试件界面时，一部分被反射形成反射波，另一部分通过试件透射进入透射杆，在实验时，要保证试件中应力的均匀性。由于入射波的作用时间比试件中应力波的传播时间要长得多，在加载过程中，试件中应力波发生多次内反射，使得试样中应力很快趋于均匀化，因此可以忽略试件内部应力波的传播效应。

试件的应变率、应变和应力可分别用下列公式计算

(3)

(4)

(5)

式中：εi(t)，εr(t)，εt(t)分别为杆中入射、反射和透射的应变；A0为杆的横截面积；E0和C0为杆材料的杨氏模量和弹性波波速；AS和LS分别为试件的原始横截面积和长度。当试件中应力达到均匀时，有

εi(t)+εr(t)=εt(t)

(6)

则上面三个公式可简化为

(7)

因此，利用上述公式就可以方便地得到材料的应力-应变数据。而且在试验过程中，要保证获得的曲线在恒应变率的条件下进行，如图4所示。通过整形片来调整使试验在恒应变率下进行。而对于动态应变率的取值，对所得到的应变率曲线有用部分进行积分，然后对积分得到的曲线进行线性拟合，线性拟合得到的直线的斜率就是应变率的取值。

图4 真实应力与应变率

2 实验结果与本构方程

2.1 实验结果分析

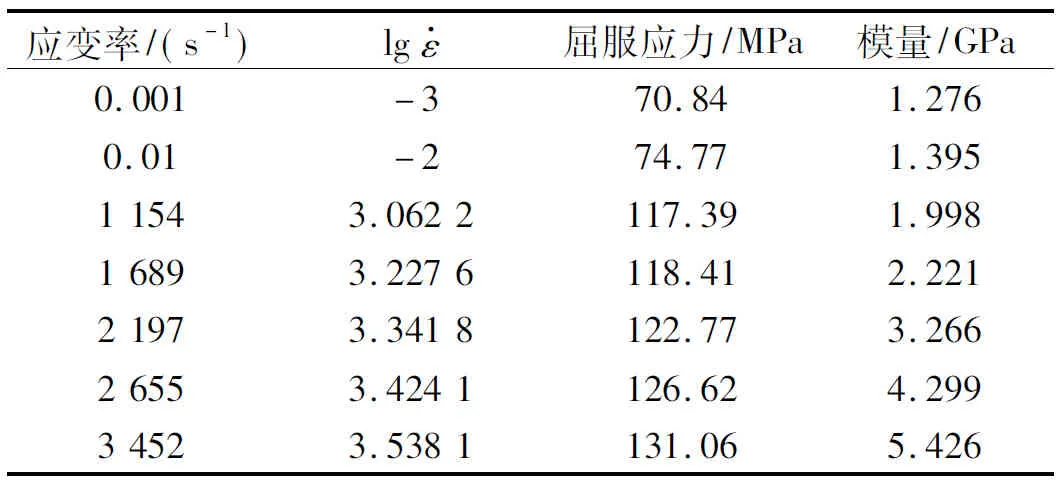
根据准静态和动态压缩所得到的实验数据，然后对实验数据进行处理，得到PC材料不同应变率下弹性段的真实应力应变曲线，如图5所示，根据图中的曲线可知，PC材料在不同应变率下表现为黏弹性行为，且随着应变率的增大，模量也随之增大，而图6为整个阶段的真实应力应变曲线。而对于屈服点的确定，由于PC材料真实应力应变曲线具有明显的弹性和塑性阶段，所以PC材料的屈服点可以定义为其在压缩时初始出现的最大名义应力，即弹性阶段和塑性应变软化阶段的分界点；而对于模量的确定，基于准静态压缩试验，我们发现弹性段弹性应变的前60%呈现为线性的，由于SHPB试验中，聚合物的弹性阶段应变率处于不断上升阶段，可能存在一定的误差，因此我们对动态压缩应力应变曲线也取弹性段弹性应变的60%进行线性拟合，得到拟合直线的斜率就为弹性阶段的模量，表2记录的是不同应变率下PC材料对应的屈服应力以及模量。

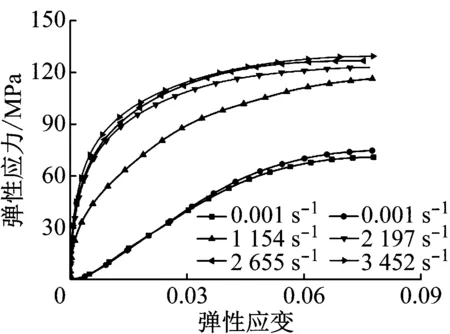
图5 不同应变率下的弹性段应力应变曲线

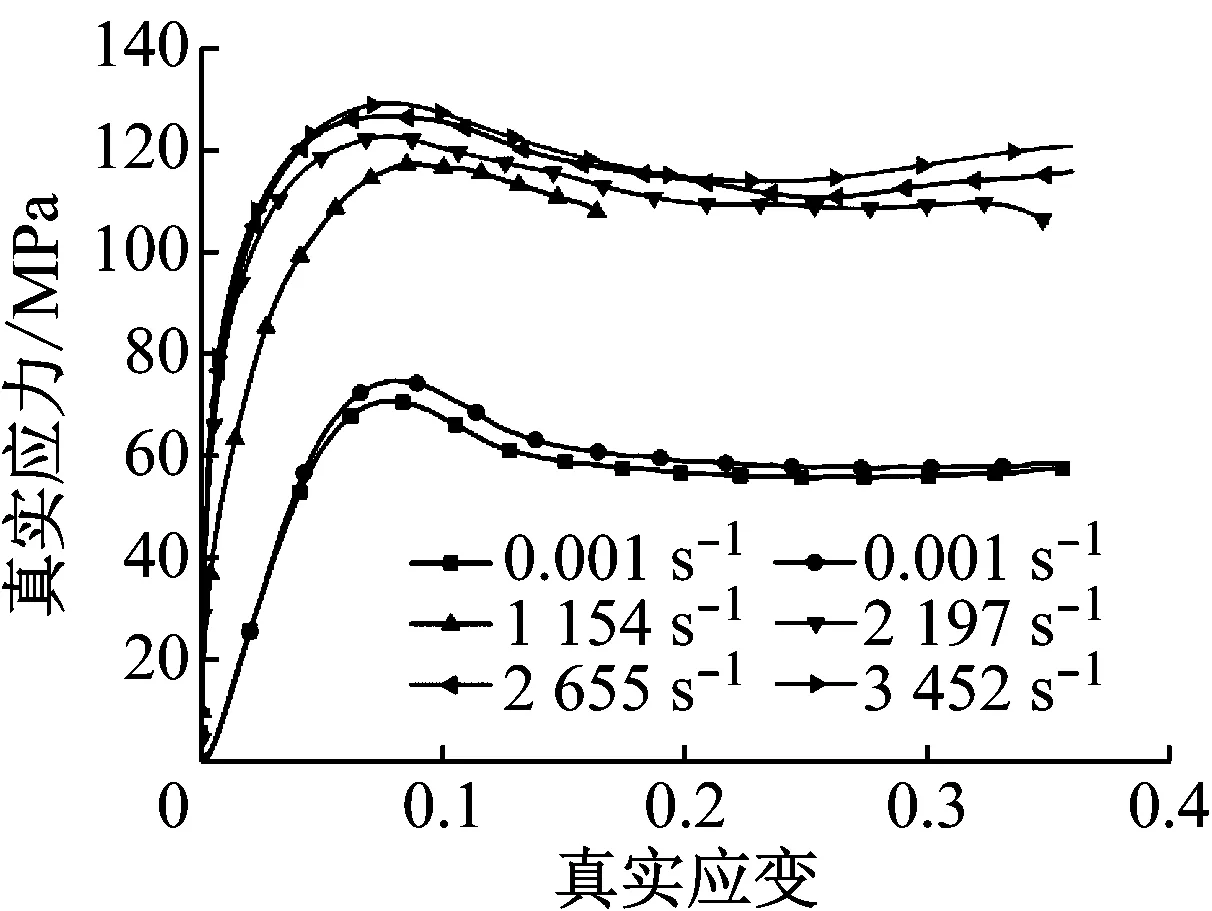
图6 不同应变率下的真实应力应变曲线

通过分析PC材料的应力应变曲线可以发现：①在不同应变率下聚碳酸酯材料对大变形有以下的响应特性：初始应力应变表现为线弹性，紧接着到达材料的屈服极限，其次是塑性阶段，依次为应变软化和应变硬化；②在不同应变率下，PC材料塑性阶段的应力应变曲线变化趋势近似相同；③PC材料在高应变率下的总应力比在低应变率下增加更迅速；④高应变率的初始弹性变形比低应变率更大。

2.2 本构方程

基于上文的分析表明，PC材料的屈服应力具有明显的应变率效应。因此，需要建立一个本构模型可以较好地描述PC材料应变率从低到高力学性能的变化。本文参考Yu等[19]根据一维流变提出的黏弹塑性本构模型，并对此做了改进，将原来模型弹性阶段非线性用线性代替，屈服点采用与应变率相关的双线性关系，塑性阶段仍采用原模型的方程，得到的模型示意图如图7所示。此本构模型可以分为三部分。第一部分描述屈服前弹性阶段，利用一个弹簧来描述弹性阶段，此模型的优点是简单而且基本，便于使用； 第二部分描述屈服点，利用屈服应力与应变率的对数呈双线性关系建立了描述屈服点的方程；第三部分为黏塑性阶段，是由软化和硬化弹簧组成，在软化过程中，软化模型是基于Boyce和Richeton的模型发展而来，而硬化模型是基于运动学变量来描述各向同性硬化黏塑性材料的理论建立的。因此，建立了如下的本构模型。

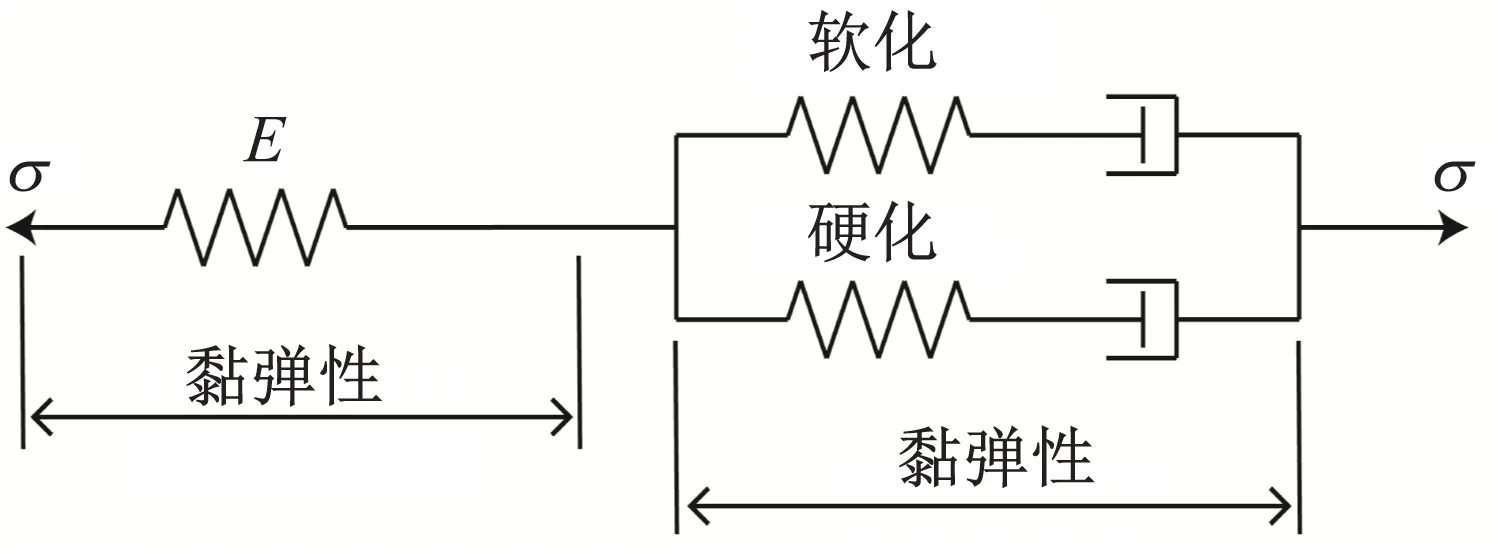
图7 改进型的PC材料本构模型示意图

(1)弹性阶段

虽然PC材料的压缩应力应变曲线弹性阶段表现出一定的非线性，但是采用考虑应变率效应的线弹性模型也可以近似描述材料的弹性阶段。为了得到材料弹性阶段的本构方程，对弹性阶段采用考虑应变率效应的线弹性模型，对于不同应变率下的模量，可以通过双线性曲线使之与应变率对应起来，如图8所示，其弹性阶段的本构方程如下

(8)

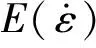
(9)

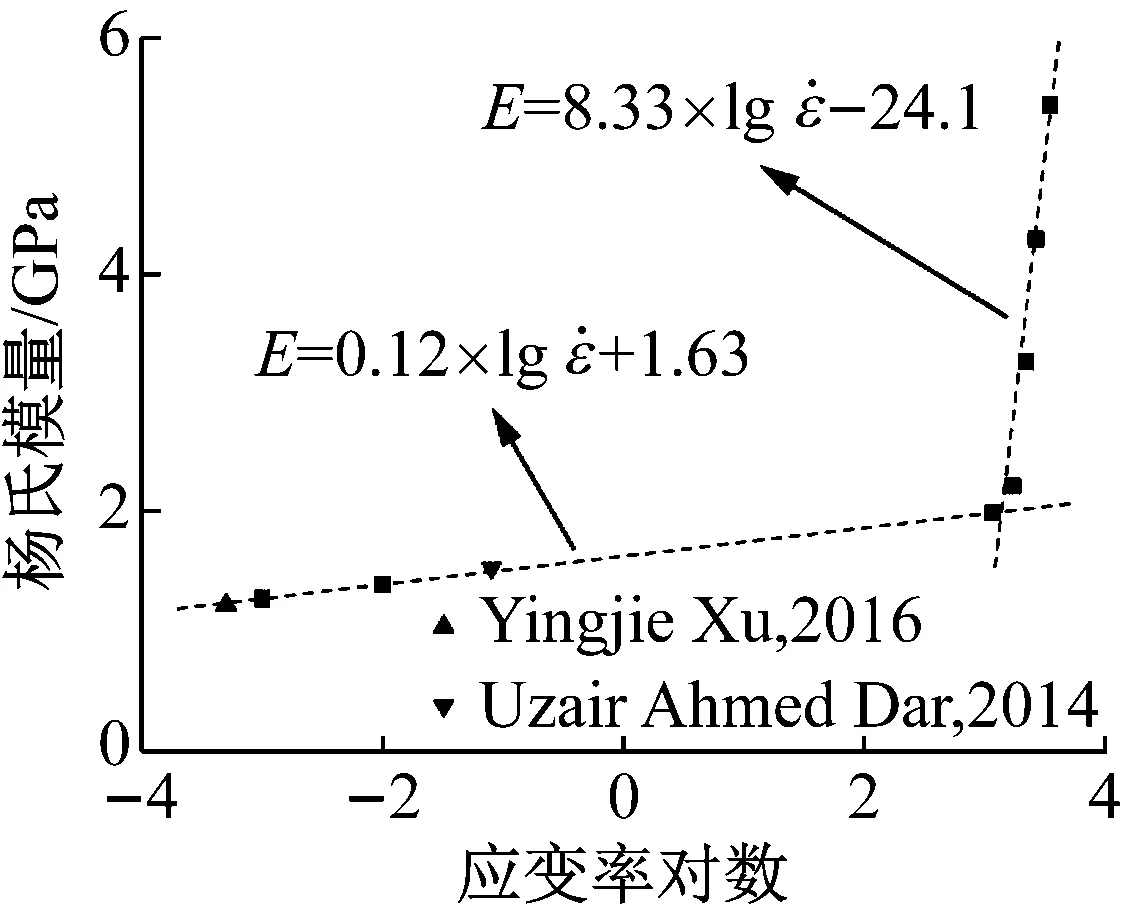
图8 模量与应变率的关系

(2)屈服应力

PC材料的屈服应力与应变率有很大的关系，即屈服应力具有应变率效应，而关于屈服应力的研究中，Wang等[20]根据实验结果得出聚合物的屈服应力与应变率常用对数呈双线性关系，对于PC材料同样采用此方法，拟合得到的曲线如图9所示，得到屈服应力的计算公式为

(10)

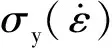
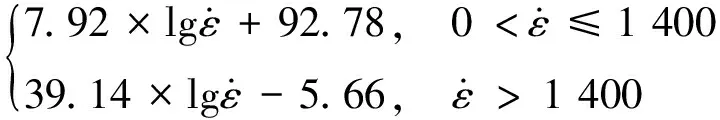
(11)

(3)塑性阶段

(12)

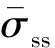
293=2.20

(13)

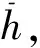
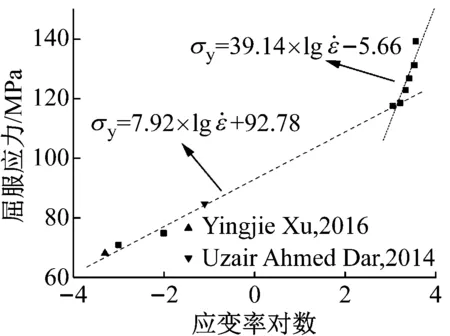
图9 屈服应力与应变率的关系

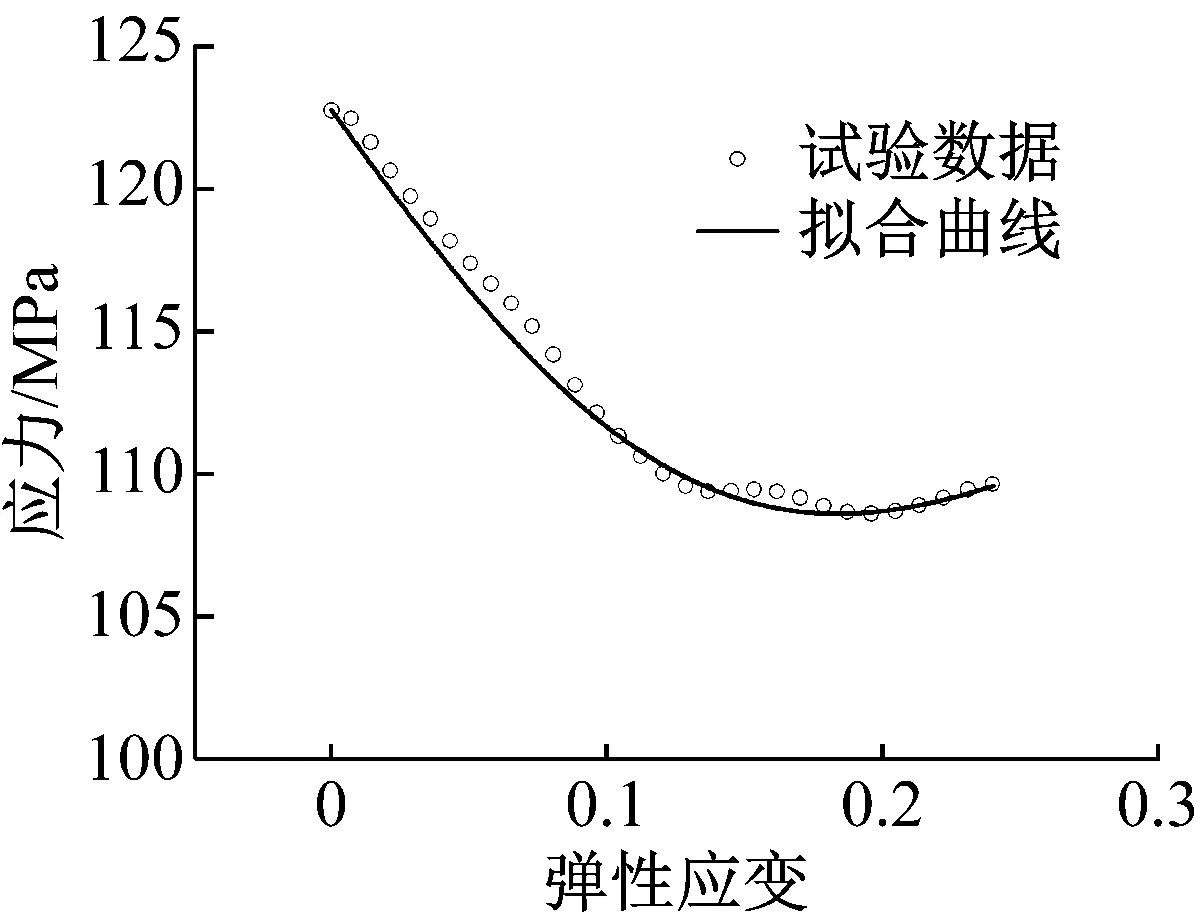
图10 塑性阶段拟合曲线

综上所述，可以得到PC材料的本构方程为

σ=

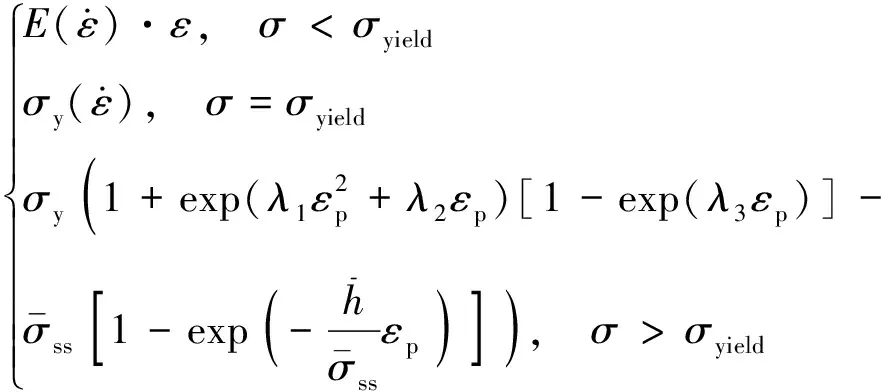
(14)

至此，PC材料本构模型中每个参数的意义已在上文进行了讨论，所有参数的取值都已列入表3中。

表3 本构方程拟合参数

3 材料模型验证与分析

为了验证上文PC材料本构模型的准确性，根据此本构方程画出不同应变率下的应力应变曲线并与试验得到的应力应变曲线进行对比，具体方法如下：首先根据式(9)模量与应变率的关系，计算出不同应变率下所对应的模量；接着根据式(11)计算出不同应变率对应的屈服应力，然后代入式(8)中计算出PC材料的屈服应变；最后根据不同应变率下的屈服应力，得到塑性应力应变曲线，结合弹性阶段就可以得到PC材料整个阶段的应力应变曲线。图11为不同应变率下PC材料的模型预测和试验得到的应力应变曲线。

图11 模型与试验对比结果

通过比较理论模型和试验结果曲线发现：准静态压缩下，本文构建的线弹性和黏弹性模型与实验得到的数据具有较好的一致性，但在屈服点附近，吻合度不高，这是由于PC材料弹性阶段具有一定的非线性，而本文采用线弹性模型，需要进一步改进该模型；对于动态压缩，理论与实验曲线弹性阶段吻合度不高，这是由于SHPB实验中，弹性阶段对应的应变率处于上升阶段，难以保持恒定，这导致得到的弹性阶段实验数据具有一定的误差，到达塑性区后，本模型采用的是应变软化与应变硬化相互作用的模型，实验数据与理论模型曲线吻合度较高。因此，本文所构建的线弹性—黏塑性本构模型可以比较准确地描述PC材料的力学行为。

4 结 论

实验研究了PC材料准静态和动态压缩的力学行为，得到了不同应变率下的应力应变曲线，通过分析其应力应变曲线，建立了PC材料的本构模型，并对实验和理论模型曲线进行了比较，得到以下结论：

(1)在压缩过程中，应变率对PC材料的力学行为有很大的影响，屈服应力随着应变率的增加而显著增加，不同应变率下塑性阶段的变化趋势大致相同，即塑性段的切向模量相同；此外，模量也随着应变率的增加而变大。