周期时变转子系统参数识别技术研究

王 志， 王建军， 刘 玉

(1.北京航空航天大学 能源与动力工程学院，北京 100191； 2.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室，沈阳 110136)

随着科技的进步，在航空航天、交通运输、能源电力等领域中的工程结构都在向复杂化、高速化和智能化的方向发展，这就导致许多结构的参数是随时间变化的，如火箭发射过程中的质量、齿轮啮合刚度等，这种时变特性常常使系统的动态特性发生重大变化，甚至会威胁到系统的稳定性，因此时变系统的参数识别研究具有广泛而重要的意义[1]。

目前，对于线性时不变结构动力学正问题和反问题的研究已趋于成熟，但时变结构的研究，因为其难度较大，还是结构动力学学科的前沿问题[2]，特别是反问题(时变参数识别问题)的研究，被认为是近期力学领域的重点研究方向。因此国内外一些学者对其进行了深入探索，并取得了丰硕的成果。史治宇、许鑫等利用系统的激励和受迫响应数据，提出了基于状态空间和小波变换的时变系统参数识别方法，并以二自由度弹簧-质量-阻尼模型为仿真算例，对系统时变参数进行了识别，算例结果验证了其方法的正确性和有效性[3-6]。庞世伟等[7-10]提出了利用自由响应数据的递推子空间方法，并通过移动质量块-简支梁模型的仿真试验，验证了该方法可以有效地辨识时变系统参数变化，且跟踪精度高，计算量小，对噪声不敏感。Shan等[11]利用连续小波变换(CWT)对时变系统进行了参数识别，并讨论了小波尺度对识别结果的影响。Bao等[12]基于新改进的希尔伯特-黄变换理论(HHT)算法对参数时变的复合梁进行了有效识别，且鲁棒性好。

以上都是以一般时变系统为研究对象，给出了仿真算例。在实际工程中存在着大量具有周期时变参数的振动系统(参激振动系统)，如齿轮系统[13-14]、非对称转子(非圆截面轴、带嵌线槽电机转子等)或裂纹转子系统等[15-16]，当前针对这种特定参激振动系统的参数识别研究还很少。

本文利用方波脉冲函数具有脱关性、正交性等优良性质，推导出参数识别递推计算公式；并利用该公式分别对二自由度周期时变仿真系统和典型非对称(方轴)转子实验系统进行了周期时变刚度识别。

1 参数识别理论及算法

结构动力学问题，包括激励、结构本身和响应三要素，即输入、系统和输出。参数识别问题，是指已知系统的输入和输出，求得描述系统特性的各种参数，属于结构动力学第一类逆问题。

一般线性时变n自由度系统由下述状态方程描述

(1)

式中：x(t)∈Rn×1为状态向量，A(t)∈Rn×n为时变系统矩阵，B(t)∈Rn×r为时变控制矩阵，u(t)∈Rr×1为输入向量。参数识别即在已知x(t)、u(t)的情况下，识别出矩阵A(t)、B(t)中的各项参数。

本文基于系统在初始状态下的自由响应数据来识别A(t)，因此设u(t)=0。

1.1 函数的方波脉冲级数展开

一个在区间[0,T)内绝对可积的函数f(t)可以在该时域内展开成一组方波脉冲级数[17]，即

f(t)≈f1g1(t)+f2g2(t)+…+

(2)

式中：fi为第i项方波脉冲系数，gi(t)为第i项方波脉冲函数。其中gi(t)定义为

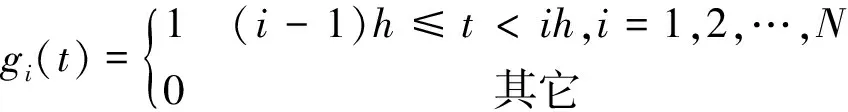
(3)

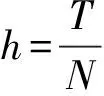
根据式(3)，经推导可知，gi(t)具有脱关性与正交性，即

(4)

(5)

式(2)两端同时乘以gi(t)，并在[0,T)上积分，由gi(t)的正交性质可得

(6)

取其三次代数精度近似，则有

f(ih)]

(7)

其截断误差为

(8)

将式(1)中的x(t)、x0、A(t)分别展开为方波脉冲级数，且设N>n，则有

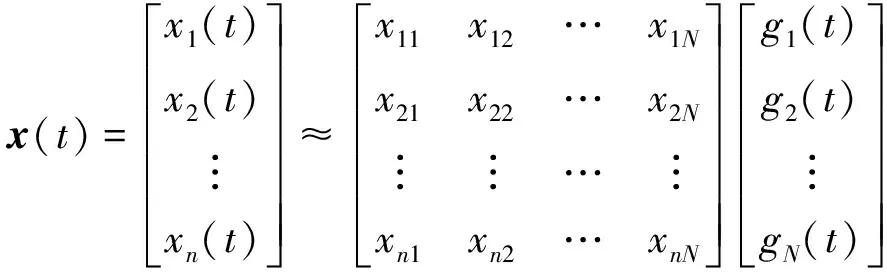
(9)

简写成

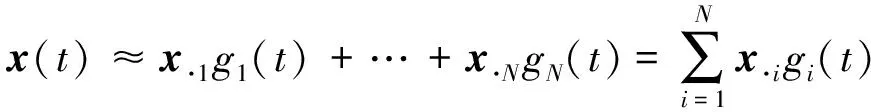
(10)

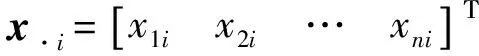
同理，可将x0、A(t)写成

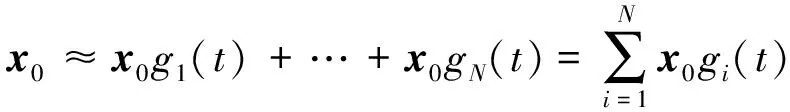
(11)

(12)

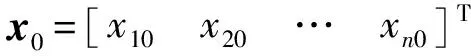
1.2 时变系统矩阵A(t)识别

当u(t)=0时，将式(1)中的状态方程等号两边进行积分得到

(13)

将各变量用方波脉冲级数展开并代入式(13)，根据方波脉冲函数的脱关性，可得

(14)

由于

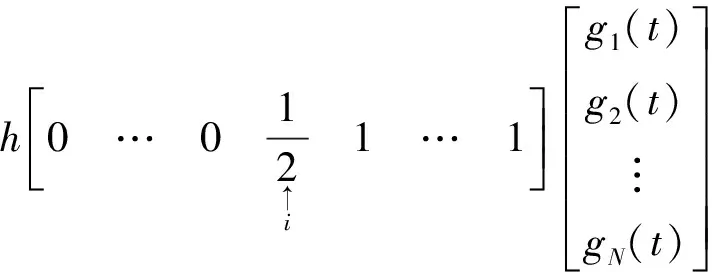
(15)

因而有

(16)

由于上述方程对t∈[0,T)内的任何t值均成立，所以令等号两边对应系数相等，可得

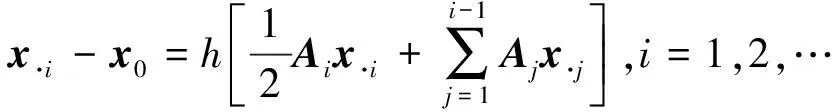
(17)

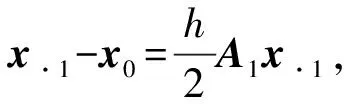
(18)

故有

(19)

式中

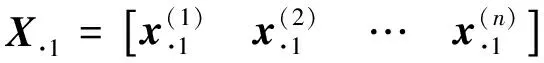
对每个不同的初始状态向量可以求出N个子区间内不同的状态响应，由于X0为n×n满秩矩阵，可得X·i也是n×n满秩矩阵，由式(19)可以解出A1为

(20)

由于

(21)

因而可得系统矩阵Ai的递推公式

(22)

1.3 周期时变振动系统刚度与阻尼矩阵识别

p自由度阻尼、刚度周期时变的振动系统动力微分方程为

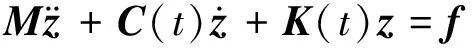
(23)

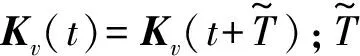
系统在做自由振动时，将式(23)用状态方程来描述为

(24)

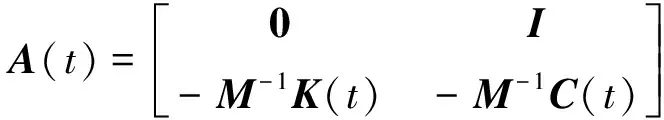
(25)

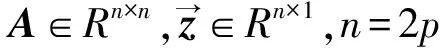
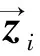
(26)

由式(25)可见，A中后p行为待求参数，为减少计算量，提高求解速度，将矩阵进行分块

从而根据式(22)可推导出刚度、阻尼参数识别递推公式(27)～(30)

(27)

(28)

(29)

(30)

对于具有周期时变参数的振动系统，根据Sylvester与Fourier理论，其自由响应的频谱为

(31)

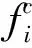
2 二自由度周期时变仿真系统参数识别

图1所示一个二自由度质量-弹簧-阻尼时变系统，质量m1=1 kg，m2=2 kg，刚度k1=1×104N/m，kc=2×104N/m，kv=5×103N/m，刚度时变频率Ω=20 rad/s、初相位φ=π/2。时变刚度k2=kc+kvcos(Ωt+φ)。为了突出研究刚度变化，现假设阻尼c1=c2=0，外界激振力f1=f2=0。

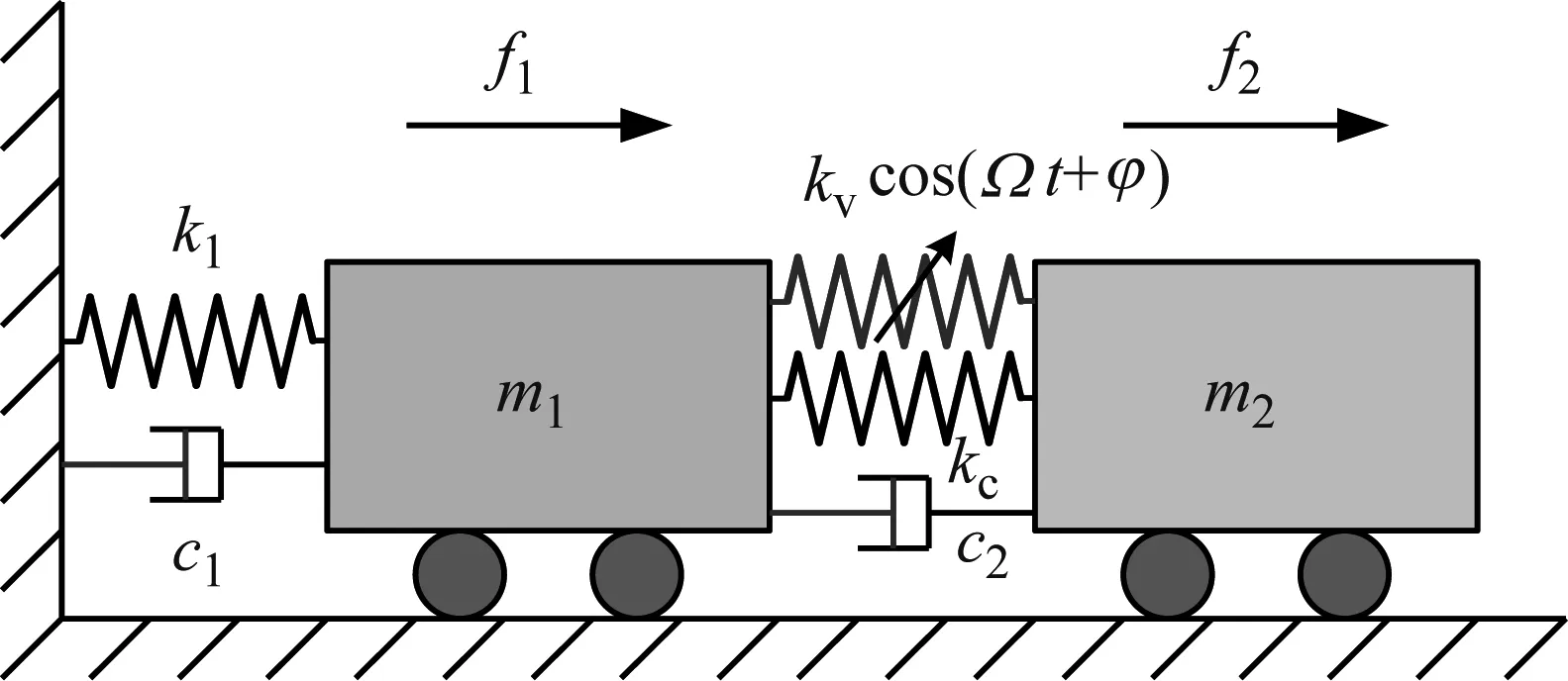
图1 二自由度刚度周期时变振动系统

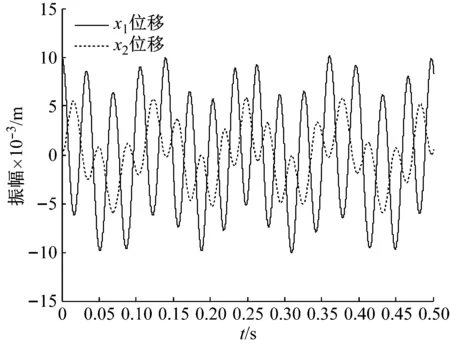
图2 二自由度刚度周期时变系统振动位移响应

对x2位移信号进行频谱分析，如图3所示。

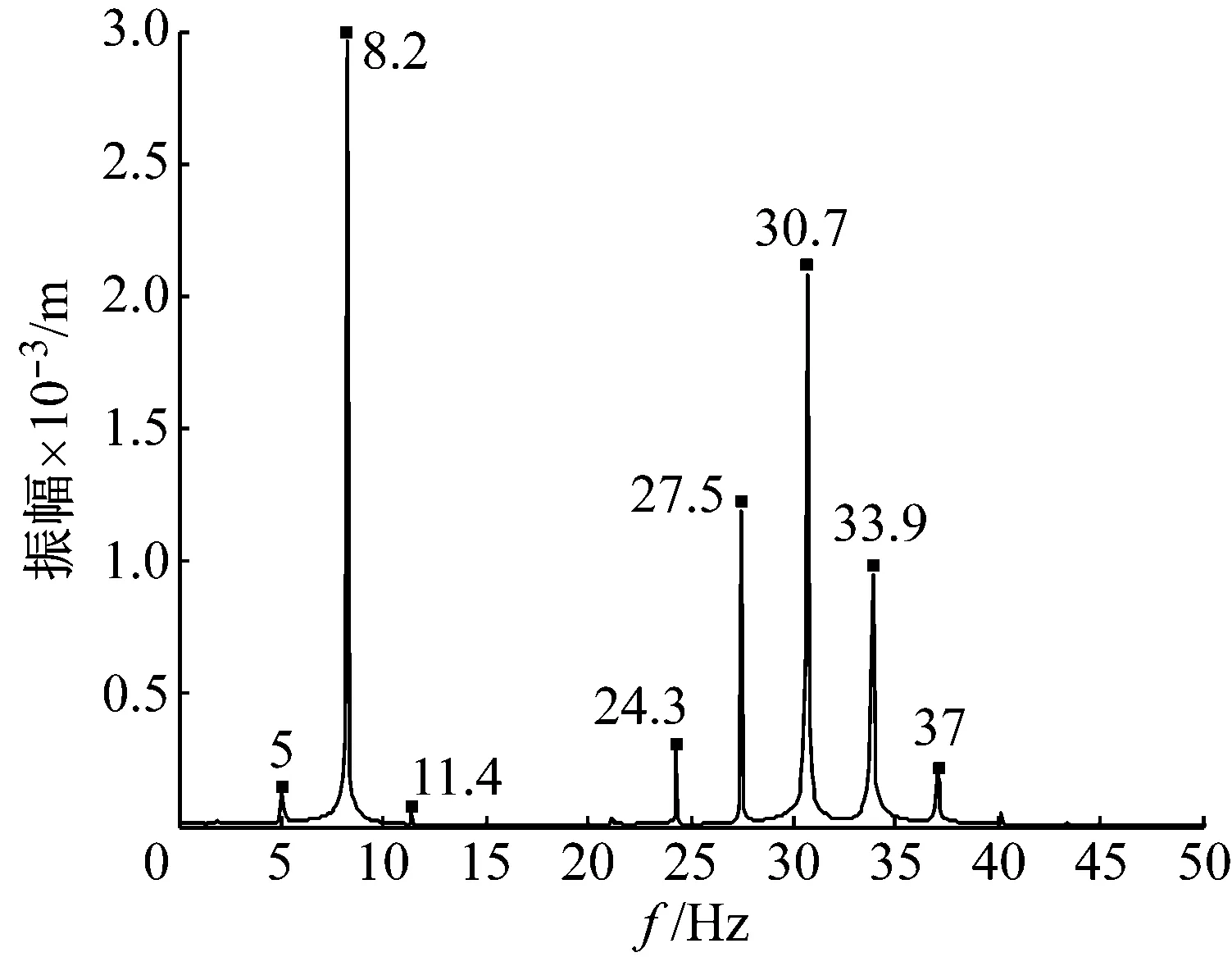
图3 x2位移频谱图

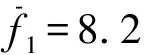
本文共进行四组不同初始状态(且线性无关)下的响应计算，根据递推公式(27)～(30)，利用MATLAB语言编制参数识别程序，时变刚度识别结果及相对误差如图4～图6所示。

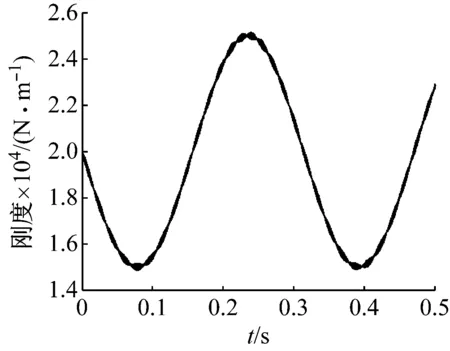
图4 时变刚度k2识别结果(时域图)

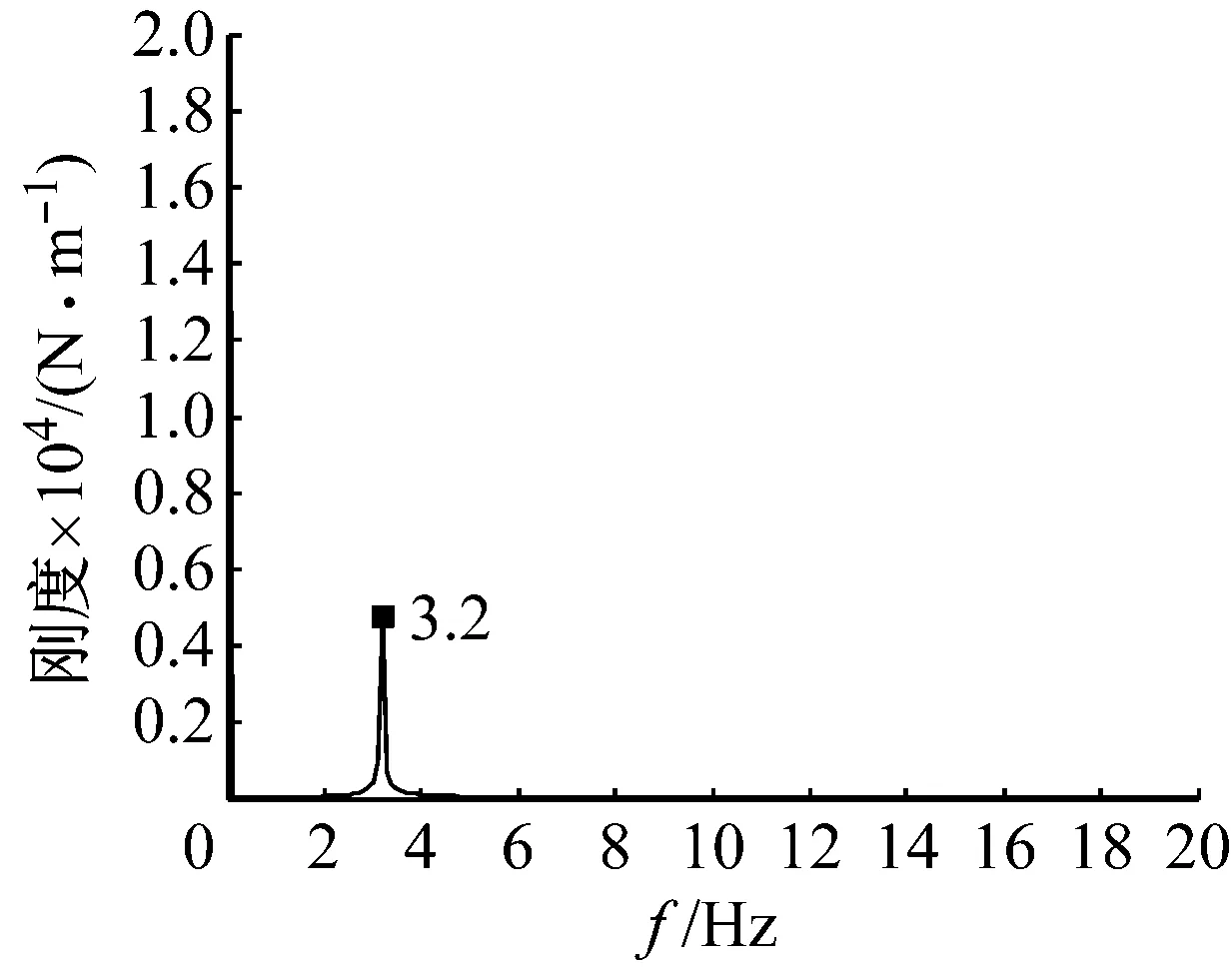
图5 时变刚度k2识别结果(频域图)

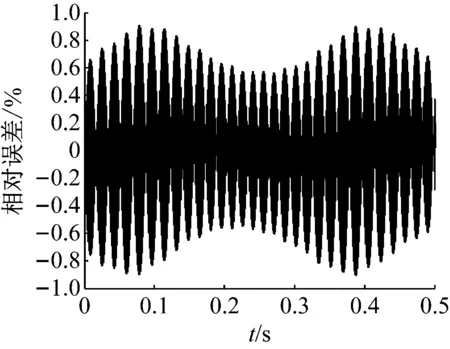
图6 刚度识别相对误差

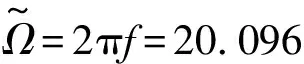
为研究不同信噪比、计算步长对识别结果的精度影响，定义识别结果的平均绝对百分误差(MAPE)为

(32)

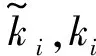
信噪比与计算步长对识别精度的影响分别如表1、表2所示。

通过表1、表2可知，信号噪声对识别结果有一定的影响，故在信号采集过程中应尽量提高信噪比；计算步长越小，识别效果越好，但相应的计算量也增大，故应根据实际要求选择合适的步长。

3 非对称转子刚度识别

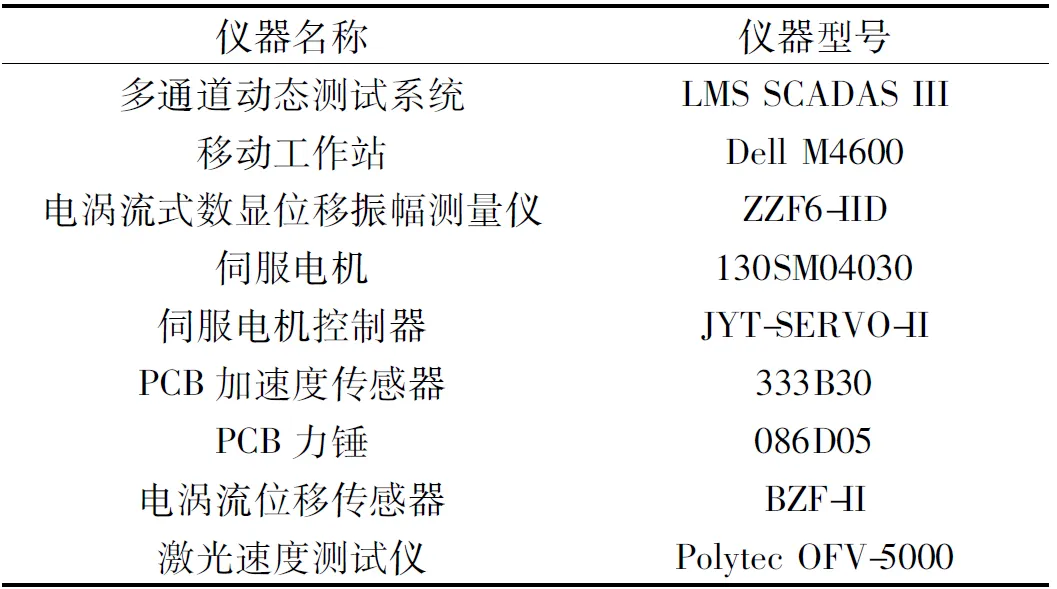
为了对本文提出的参数识别方法进行实验验证，搭建具有刚度周期时变特性的非对称(方轴)转子实验系统，如图7所示；实验所用仪器设备如表3所示。对非对称转子系统进行锤击实验(用力锤与水平成45°敲击轴中心，即盘旁)，利用LMS Test.lab软件进行数据采集与处理。

图7 非对称转子实验系统

非对称转子结构如图8、图9所示，转轴材料为30CrMnSi，轮盘材料为45#钢，相关参数为：l=475 mm，d轴=14 mm，h=8 mm，ρ轴=7 750 kg/m3，E轴=2.01×1011Pa，μ轴=0.227，D盘=212 mm，ρ盘=7 850 kg/m3。为了实现轴的非对称性，在轴上进行部分切割处理，使其在相互垂直的两个方向上抗弯刚度不同(方轴)。实验中，调节转速控制器，使转子在n=720 r/min下稳定运转，这样轴在水平、垂直方向上的抗弯刚度则随转速时变；用力锤对转子系统进行冲击响应实验，通过降低转子不平衡度与滤波的方法来消除转子在离心力下的不平衡响应影响，突出转子在脉冲激励后的自由响应。

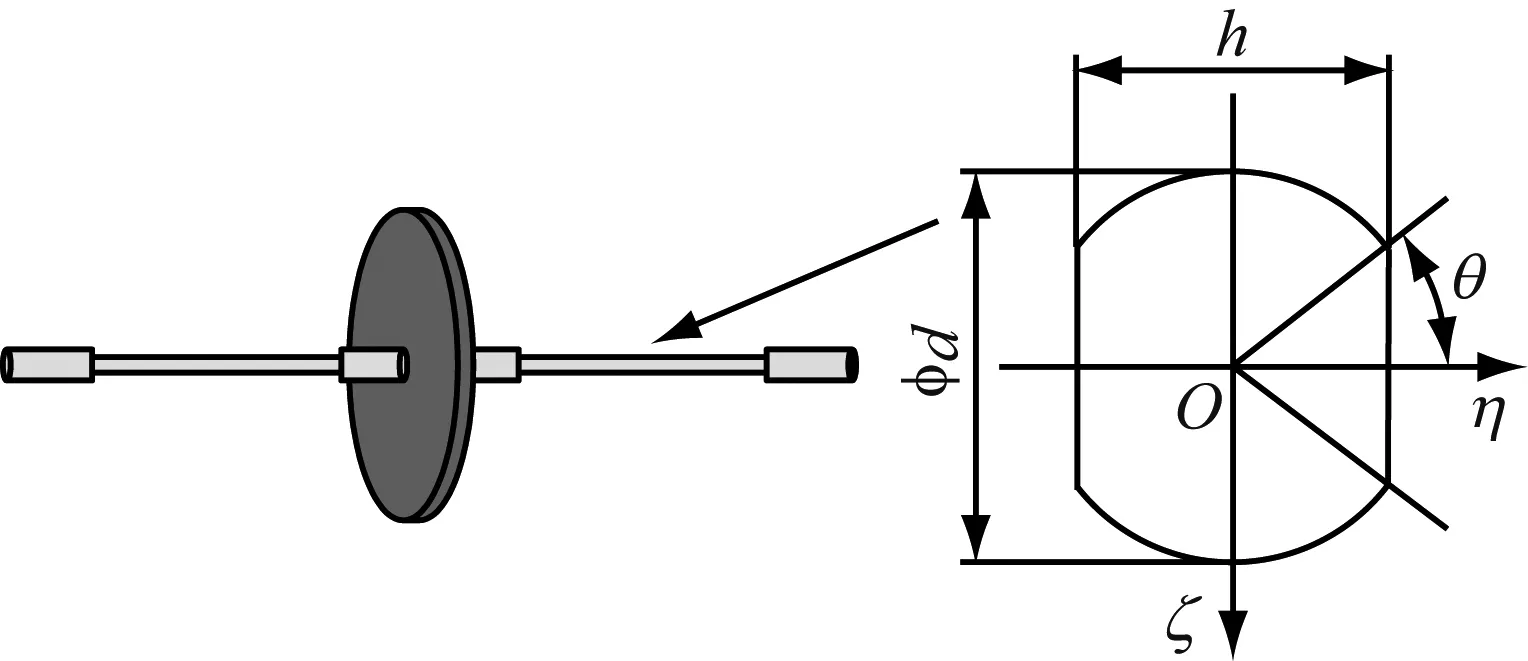
图8 非对称转子结构示意图

图9 非对称转子实物与测点分布图

对非对称转子系统进行多次锤击测试，利用电涡流位移传感器采集轴中心的振动位移(水平、竖直方向)，用激光速度测试仪采集轴中心水平方向振动速度，用加速度传感器采集转子支承处的振动加速度(水平、竖直、轴向)。某次测试水平方向位移与速度响应分别如图10、图11所示。

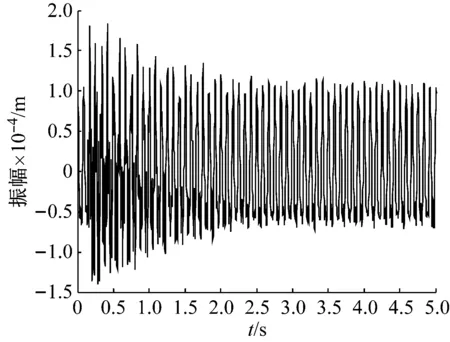
图10 测点8水平方向位移时域响应

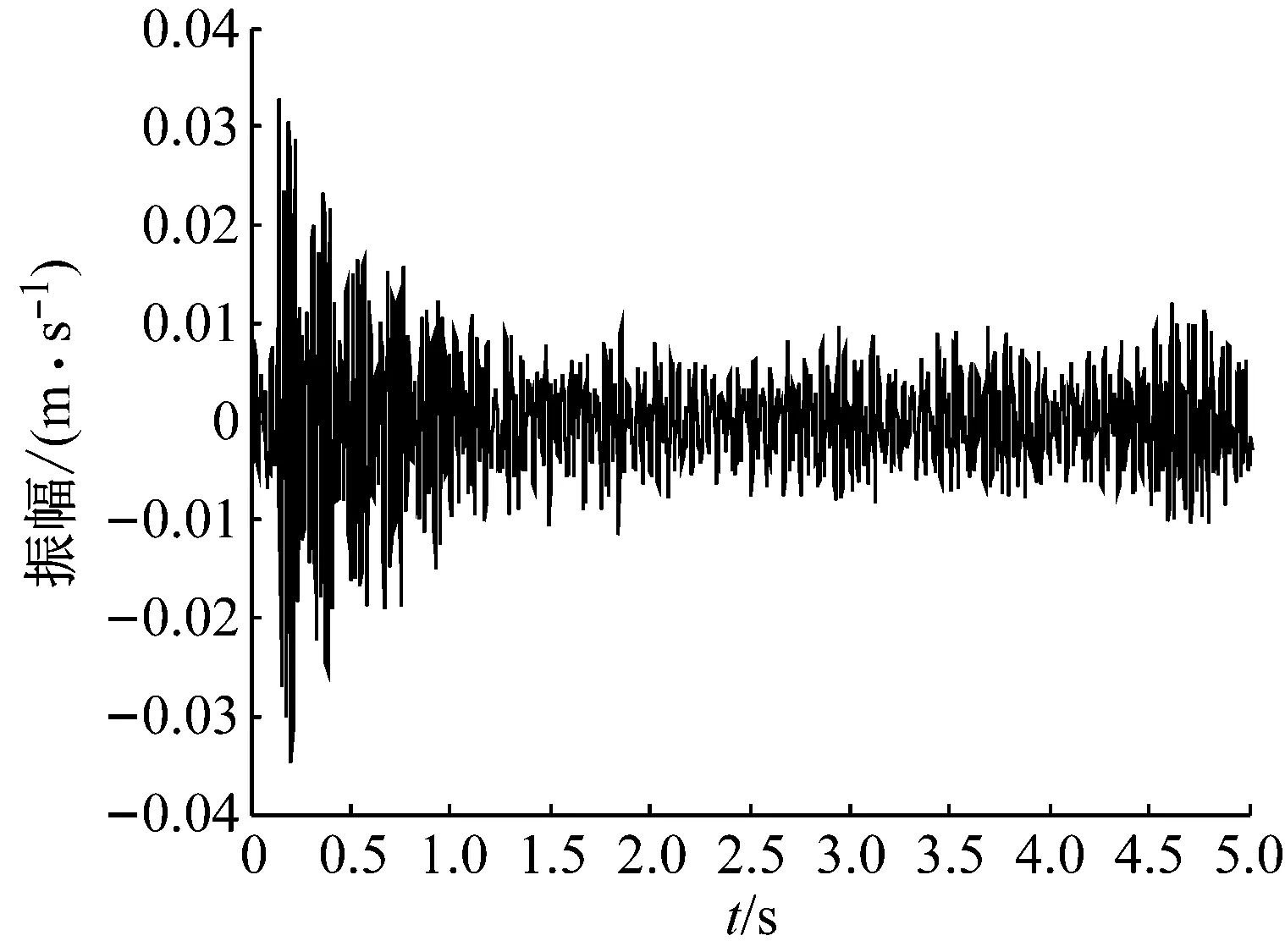
图11 测点9水平方向速度时域响应

利用本文的方法对实验中采集到的信号进行分析，从而得到非对称转子的时变刚度，如图12所示。

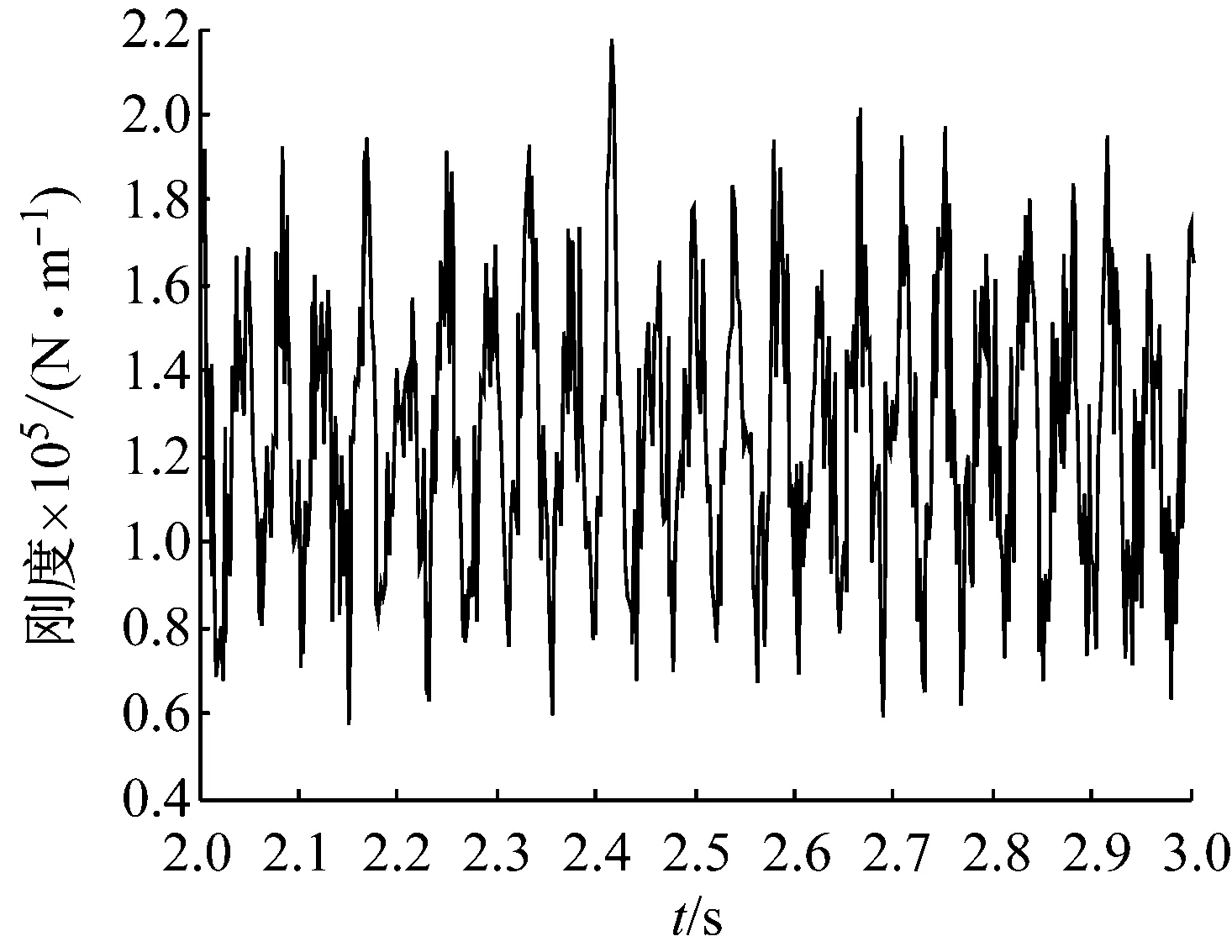
图12 非对称转子水平方向刚度变化曲线

可见运用本文方法识别出的非对称转子水平刚度由常值和周期时变两部分组成，由于数据采集中噪声的存在，识别出的刚度曲线存在一些毛刺。对该曲线进行频域分析，如图13所示。

由图13可见，本文所识别出的刚度为与kc=1.25×105N/m，kv=3.76×104N/m，与利用ANSYS有限元软件计算出的kc=1.27×105N/m，kv=3.82×104N/m相近。非对称转子水平刚度变化具有明显的周期性，频率成分为f=24 Hz，恰为转子转频fn=720/60=12的二倍，与转子转一周刚度时变二次相符。不同计算步长(即不同采样频率)对刚度识别MAPE的影响如表4所示。可见，当选择合适的步长(本实验选取10-4s)时，平均绝对百分误差小于1%。

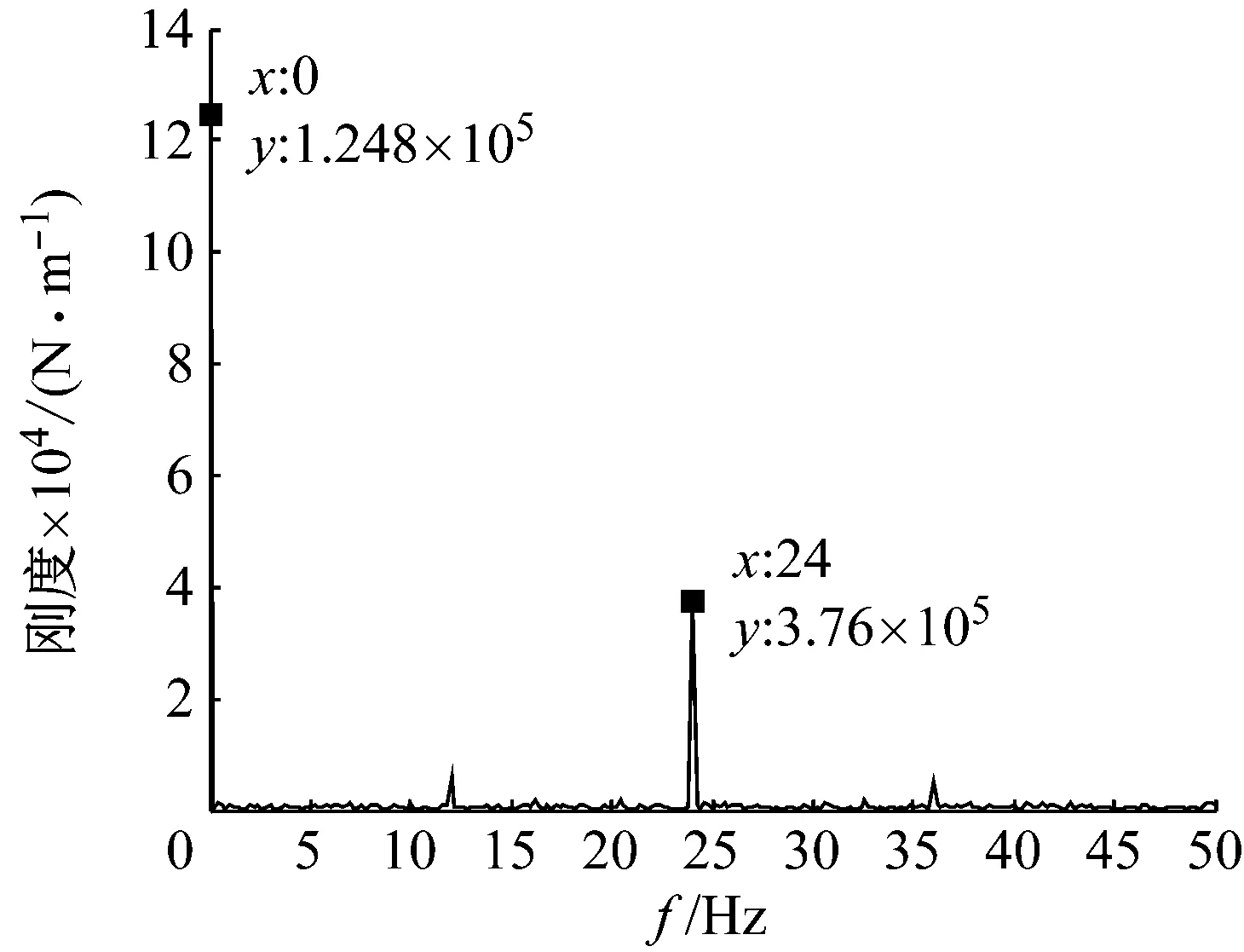
图13 非对称转子水平方向刚度频谱图

4 结 论

(1)本文所推导出的周期时变转子系统参数识别递推公式具有结构简明、计算省时等优点。

(2)信号噪声对识别结果有一定的影响，故在信号采集过程中应尽量提高信噪比；计算步长越小，识别效果越好，但相应的计算量也增大，故应根据实际要求选择合适的步长。

(3)通过对二自由度数值仿真模型和实际周期时变转子系统分别进行参数识别，均较准确的识别出了时变刚度参数，其平均绝对百分误差分别小于0.5%与1%，从而验证了本方法的正确性和有效性。

(4)本文为齿轮、裂纹转子等具有周期时变参数的工程机械结构的参数识别及故障诊断提供一种新方法，有较大的工程应用价值。