旋转叶片-柔性机匣碰摩振动响应分析
郭旭民, 孙 祺, 马 辉,2,3, 孙 帆
(1. 东北大学 机械工程与自动化学院, 沈阳 110819;2. 东北大学 航空动力装备振动及控制教育部重点实验室, 沈阳 110819;3. 上海交通大学 机械系统与振动国家重点实验室, 上海 200240)
航空发动机常运行在高温、高压和高转速环境下,同时为了提高航空发动机性能,需尽量减小叶片和机匣间隙,因此在这种极端工况下极易导致叶片-机匣碰摩。
由于这种问题的存在,所以国内外学者对叶片-机匣碰摩模型进行了大量的研究。Sinha[1]研究了带叶片的柔性转子与刚性机匣的碰摩动力学特性以及碰摩导致的系统复杂振动响应。Lesaffre等[2]基于Sinha提出的转子叶片模型,采用劳斯-赫尔维茨判据分析了旋转梁和柔性环碰摩稳定性。太兴宇等[3]将叶片等效为气动载荷和离心载荷作用下的悬臂梁,将机匣简化为单质量弹簧-阻尼模型,推导了叶片-机匣碰摩表征模型。Ma等[4]由能量守恒定律推导了新的旋转叶片和弹性机匣碰摩模型,并讨论了侵入量,机匣刚度,摩擦因数,叶片几何尺寸对法向碰摩力的影响。
在圆柱壳振动特性方面,学者们也做了较多研究。Hemmatnezha等[5]通过实验与数值模拟相结合的手段研究了加筋复合材料圆柱壳的自由振动特性,并对比了不同表面厚度和边界条件对壳固有频率的影响。Rodrigues等[6]研究了模态耦合对直接激励下的圆柱壳的动力学影响,结果发现圆柱壳在最低阶固有频率附近的几个相近频率处会产生多个共振。Song等[7]基于Donnell壳理论采用瑞利-李兹法对任意边界条件下旋转层压圆柱壳的行波振动进行了分析,通过在自由边界条件下引入弹簧,并改变弹簧刚度来进行任意边界条件下圆柱壳的行波振动分析。王宇等[8]针对固支-自由约束条件下的薄壁圆柱壳,基于Love壳体理论,利用振型叠加法研究了受径向谐波激励和冲击载荷激励时圆柱壳的振动响应特性。李晖等[9]搭建了4种不同激励形式的测试系统,对圆柱壳固有频率进行了试验研究,并提出了约束态下薄壁圆柱壳固有频率的测试流程。曹志远[10]系统介绍了壳体动力学基本理论和研究方法,为国内板壳动力分析方面的研究提供了必要的基础知识。
根据一些学者的实验测试发现,叶片-机匣单点或局部碰摩的接触力类似于周期性脉冲力[11-12],根据这种特定的碰摩情况,一些学者给出了基于脉冲力模型的叶片-机匣碰摩模拟方法。Turner等[13-14]将碰摩力假定为脉冲力,采用有限元法研究了叶片-机匣碰摩时外力作用时间和最大叶片变形的关系,分析了叶片在不同碰摩情况下的振动形式。太兴宇等[15]采用Timoshenko梁建立了旋转叶片在脉冲力加载下的动力学方程,并对不同转速下的叶片动力学特性进行数仿真。Legrand等[16]根据机匣叶盘系统的二维模型,分析了叶盘在机匣k节径模态振型下的接触问题,并分析了转速对叶片-机匣碰摩的影响。
通过上述分析发现,现阶段国内外学者对叶片-机匣碰摩的研究多关注在旋转叶片的动力学建模方面,但在机匣建模方面,则将机匣简化为单质量弹簧-阻尼或柔性环。而Rodrigues等对圆柱壳振动特性的研究也取得了丰富的成果。本文则将两者结合,将机匣简化为圆柱壳模型,基于ANSYS有限元软件,建立新的旋转叶片-柔性机匣碰摩模型,着力探究碰摩对机匣节径振动的激发规律,同时通过对比本文模型和集中质量点模型来比较两种模型下碰摩对叶片和机匣振动响应的影响。
1 旋转叶片-机匣振动的有限元动力学模型
旋转叶片-机匣振动的动力学方程可表示为
(1)
式中:Cb和Cc分别为叶片和机匣的阻尼矩阵,这里均采用瑞利阻尼进行计算,其表达式如下
Cc=Cb=αMb+βKb
(2)
式中
其中:ω1和ω2分别为叶片的第1,2阶固有频率;ξ1和ξ2分别为对应的第1,2阶模态阻尼比。其他符号的描述见参考文献[17]。

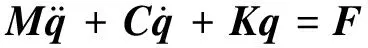
(3)
机匣采用Shell281单元来模拟。机匣的约束方式为简支约束,即机匣一端的所有节点约束3个平动方向自由度,另一端的所有节点约束除轴向外的其他2个平动方向自由度。接下来,本文基于机匣固有特性对网格进行了收敛性检查(见表1)。值得说明的是,对圆柱壳划分网格时,周向网格数用p表示,轴向网格数用q表示。从表1中可以看出网格数量为256×8时,圆柱壳的固有频率已经收敛。因此,在分析叶片-机匣碰摩响应时,圆柱壳采用的网格数为256×8。在本文研究中,机匣参数设置如下:长度Lc=0.1 m,内径Rc=0.307 12 m,厚度hc=0.002 m,弹性模量Ec=125 GPa,泊松比υc=0.3,密度ρc=4 370 kg/m3。
图1为旋转叶片-柔性机匣有限元模型示意图,其中OcXYZ为整体坐标系,Ω为叶片转速。这里的机匣中曲线是指机匣中曲面上Lc/2处的圆。叶片采用Beam188单元来模拟,沿径向等分为20份,共21个节点,忽略叶根-圆盘榫连结构的影响,叶根节点(节点1)约束形式为全约束。本文假设叶片-机匣在碰摩过程中,叶片表面受到均布的气动力作用,并且考虑叶片因旋转导致的科氏力效应、旋转软化效应和离心刚化效应。
图2为本文所研究机匣模型的前3阶模态振型(m,n),其中,m表示轴向半波数,n表示周向波数。

(a) 整体振型
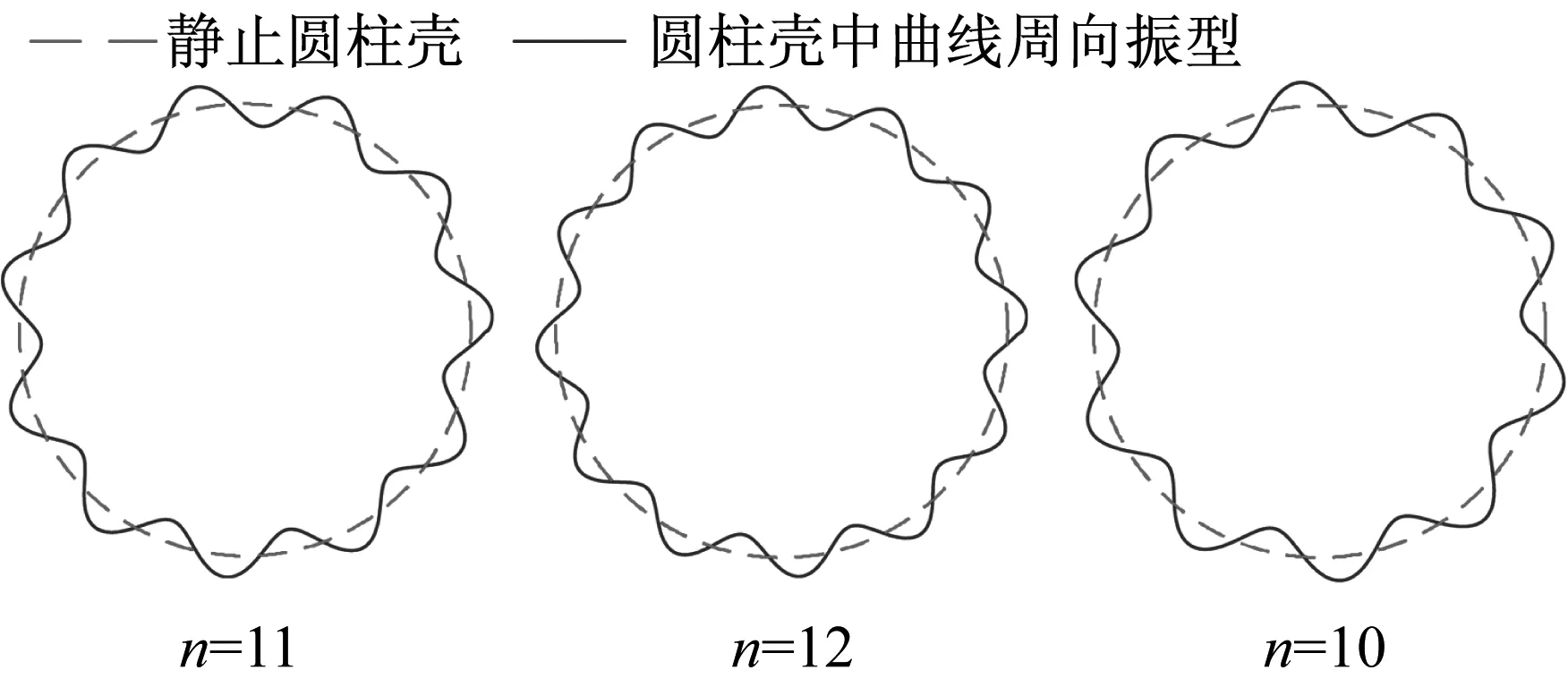
(b) 周向振型
2 碰摩力模型建立

由几何关系推导叶尖与机匣内壁间的初始间隙函数
PQ2+OQ2=OP2
(4)

图3 旋转叶片-柔性机匣碰摩示意图
((rg+ggap)sin(Ωt+φ))2+
(5)
对上式求解可得到初始间隙函数ggap表达式为
(g0-cmin)cos(Ωt+φ)-rg
(6)

(7)
每个载荷步下都要判定叶尖与机匣之间是否发生碰摩。叶尖节点的侵入量δi的表达式如下
(8)
当侵入量大于0时发生碰摩,在叶尖节点上施加法向和切向碰摩力,同时在对应的机匣节点i上施加大小相等方向相反的法向和切向碰摩力。当侵入量等于0时不发生碰摩,即:
(9)
Ft=μFn
(10)
式中,Fn为法向碰摩力;Ft为切向碰摩力;μ为摩擦因数。fn的表达式如下
(11)

叶片旋转过程中叶片表面始终受到均布的气动力的作用,叶片所受气动载荷表达式如下[18]
Fe=Fe1sin(neΩt)
(12)
式中,Fe1=225.73为气动力载荷的幅值(N/m);ne=20为障碍数目。
根据以上分析,得出模拟碰摩过程的流程图,如图4所示。

图4 叶片-柔性机匣碰摩过程流程图
3 圆柱壳与集中质量点模型响应对比
现有模型在判断叶片-机匣碰摩时大多是将机匣简化为集中质量点来考虑,该模型在叶尖与机匣的最小间隙处用一个质量弹簧-阻尼系统来模拟机匣,详见参考文献[3],这样做虽然处理起来简单但却忽略了机匣柔性对碰摩的影响。现在相同条件下,分别将机匣简化成集中质量点模型和圆柱壳模型,对两种模型的碰摩响应进行对比,结果如图5、图6和图7所示,叶片几何参数及碰摩仿真参数见表2。
图5中的集中质量点模型(集中质量点质量1.67 kg,弹簧刚度2.3×106N/m,机匣径向阻尼1 000 N·s/m)的简化原则是使集中质量点模型下的弹簧刚度与圆柱壳模型下的机匣等效刚度相同。从图5(a)可以看出机匣简化为圆柱壳模型时的最大法向碰摩力Fn比机匣简化为集中质量点模型时的最大法向碰摩力小,说明将机匣简化为圆柱壳模型后能更多的考虑机匣柔性对碰摩的影响。从图5(c)频谱图可以看出两种模型对叶尖弯曲位移的影响主要体现在幅值上,而在弯曲位移的频率成分上几乎一致。两种模型下叶尖弯曲位移都会在5fr(fr为叶片的转频)与20fr出现幅值放大现象,这是因为5fr(1 083 Hz)与叶片的1阶动频(1 090 Hz,对应叶片的一阶弯曲)接近,而20fr(4 333 Hz)与气动力频率相同,会产生共振。
图6中的A′为第1种机匣简化为集中质量点模型的机匣节点(集中质量点质量1.67 kg,弹簧刚度2.3×106N/m,机匣径向阻尼1 000 N·s/m);A″为第2种机匣简化为集中质量点模型的机匣节点(集中质量点质量1.67 kg,弹簧刚度2×108N/m,机匣径向阻尼1 000 N·s/m),这种简化原则是使集中质量点模型的1阶固有频率和圆柱壳的1阶固有频率相同;A、B、C、D分别对应机匣上的4个节点(见图1)。从图6可以看出,不同模型下机匣的径向位移响应有较大的区别。第1种集中质量点模型下的机匣径向位移在转频fr(216.5 Hz)处出现幅值放大现象,这是因为转频fr和机匣的固有频率(186 Hz)接近;第2种集中质量点模型的机匣径向位移在8fr(1 732 Hz)处出现幅值放大现象。机匣上的A节点为碰摩发生处,所以这一节点处的径向位移最大,且在8fr处出现幅值放大现象,机匣上其他3个节点为非碰摩处,它们的响应曲线形状相似,也会在8fr(1 733 Hz)处出现幅值放大现象。图6(c)和(d)为圆柱壳机匣上不同节点的径向振动频谱图(每隔8个节点做一个FFT),从图中可以看出,局部碰摩点及附近节点处的响应从fr到7fr都存在幅值,而远离碰摩位置的节点从8fr开始才有幅值,并且这种频率变化存在一个渐变的过程。

表2 叶片几何参数及碰摩仿真参数

(a) 法向碰摩力

(b) 叶尖弯曲位移时域图

(c) 叶尖弯曲位移频谱图

(a) 机匣上不同节点的时域图

(b) 机匣上不同节点的频谱图
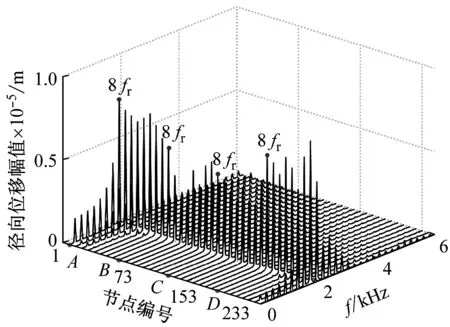
(c) 圆柱壳机匣上不同节点处的频谱图

(d) 圆柱壳机匣上不同节点处的频谱图(俯视)
图7中(a1)~(d1)分别为叶片转到机匣的0 (t=0.075 2 s)、π/2 (t=0.076 4 s)、π (t=0.077 5 s)和3π/2 (t=0.078 7 s)处时机匣变形后的位置图,叶片在A处与机匣发生碰摩,其他3处位置不发生碰摩。这里的变形是机匣中曲线上各节点的径向位移放大1×104倍后和机匣半径叠加后的效果图。从图7(a1)可以看出,机匣上A节点处的局部变形明显比其他节点处的变形大,而集中质量点模型的机匣变形是一个整体变形,在碰摩发生时机匣会整体向右平动一段距离,且变形量比圆柱壳模型的变形量小。采用圆柱壳模型后,在碰摩发生时机匣变形量大,所以叶尖侵入到机匣的侵入量小,碰摩力也就比集中质量点模型的碰摩力小,同时还可以明显观察到碰摩激发出的机匣的节径振动。图7(a2)~(d2) 为对应时刻的机匣整周径向振动响应时域图,图7(a3)~(d3)为对应时刻的机匣整周径向振动响应频谱图,该图通过机匣整周径向位移响应数据延拓10份后进行傅里叶变化得到。由频谱图可知机匣的径向振动在7节径(1 964.7 Hz)、9节径(1 764.9 Hz)、10节径(1 713.1 Hz)和13节径(1 755.0 Hz)都有较大的幅值,说明在碰摩导致的机匣变形中这四个模态都起到了主导作用。这是因为8fr(1 733 Hz)与机匣的第三阶频率(1 713.1 Hz,对应(1,10)模态振型),第四阶频率(1 755.0 Hz,对应(1,13)模态振型)和第五阶频率(1 764.9 Hz,对应(1,9)模态振型)都比较接近,而9fr(1 950 Hz)与机匣的第九阶频率(1 964.7 Hz,对应(1,7)模态振型)接近,所以最终的机匣变形是以7、9、10和13节径为主导的耦合形式。当叶片与机匣发生碰摩时,碰摩节点A处的径向变形非常明显。机匣变形随着时间不断变化,主导模态的峰值响应降低。

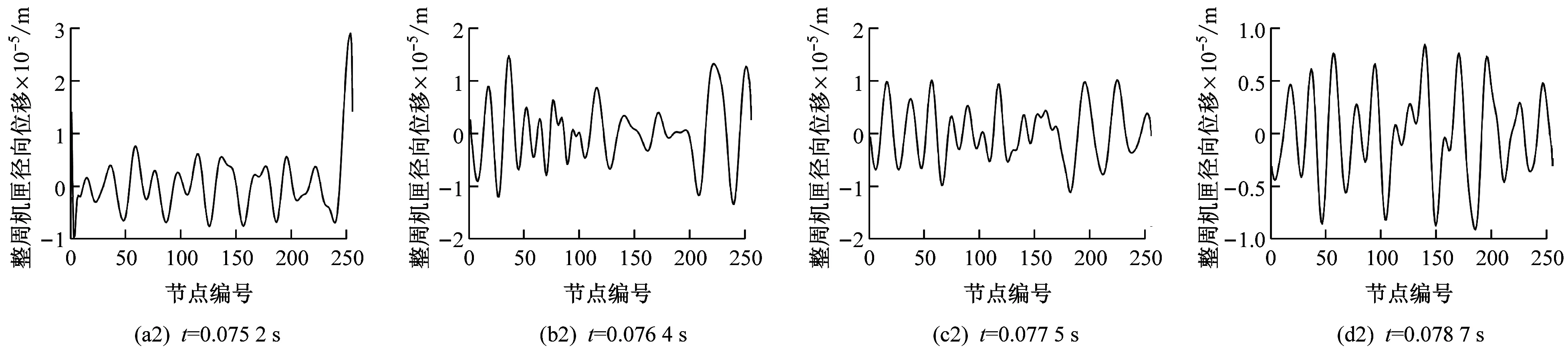

图7 不同时刻的机匣整周径向振动响应
4 结 论
为了探究旋转叶片-柔性机匣碰摩对机匣节径振动的激发规律,本文基于ANSYS有限元软件,采用壳单元建立的圆柱壳模型来模拟机匣,建立了旋转叶片-柔性机匣碰摩模型。通过计算动态间隙函数、机匣节点径向位移和叶尖节点径向位移来确定每个载荷步下叶尖节点和机匣对应节点间的间隙,从而判定碰摩是否发生。通过分析将机匣简化为圆柱壳模型后碰摩对叶片振动响应,机匣振动响应及机匣节径振动的影响,得到如下结论:
(1) 机匣简化为圆柱壳模型后可以考虑碰摩对柔性机匣节径振动的影响,而且相比于集中质量点模型,碰摩力和叶尖弯曲位移响应均呈现出降低趋势。
(2) 柔性机匣碰摩节点处的径向位移要大于非碰摩节点处的径向位移,且碰摩节点和非碰摩节点径向位移的频率成分有较大区别。主要体现在碰摩节点及附近节点处频率成分中会有低倍转频的出现,而远离碰摩处的节点处仅在高倍转频有响应。
(3) 圆柱壳模型可以考虑碰摩过程中机匣的局部变形,并且能明显观察到碰摩激发出的机匣的节径振动。就本文模型而言,碰摩激发的机匣变形是以7、9、10和13节径为主导的耦合形式。

