一种改进的有限频域状态反馈H∞控制方法研究
王兴野, 张进秋, 刘义乐, 毕占东, 李国强
(陆军装甲兵学院 车辆工程系, 北京 100072)
以外界扰动对输出的影响最小为基本控制思想的鲁棒H∞控制是近年来发展起来的一种控制性能十分优异的控制算法,特别是1994年S.P.Boyd等有关线性矩阵不等式(LMI)的专著问世以及美国The MathWorks公司推出MATLAB LMI Toolbox后,H∞控制器的设计可以转化为一组LMI,并利用MATLAB进行求解,使H∞控制成为了一种方便实用的控制器设计方法,并在近年来在车辆悬架的振动控制上也有了较为深入的研究,对于处理控制中的时滞问题[1-3]、模型不确定[4-6]和非线性问题表现出了较好的控制性能。由ISO2631国际标准可知,对于垂直方向上振动而言,人体对4~8 Hz频域内的振动最为敏感。因此,在控制器设计的过程中,有限频域振动控制成为了近年来的国内外研究的热点之一[7-10]。
Sun等[11-12]基于广义KYP引理[13]理论推导了主动悬架有限频域H∞控制定理,认为比全频域H∞控制能更好的提高车辆的乘坐舒适性。在有限频域状态反馈H∞控制器设计时,文献中所采用的设计方法外界扰动输入能量的最大值相当于wmax=ρ/ε,而全频域的H∞控制器外界扰动输入能量的最大值相当于wmax=ρ/γ2。仿真验证中,参数取值ε=10 000,然而求解全频域状态反馈H∞控制器时发现,γ2始终接近于81,可见εγ2,当ρ取相同值时,两种控制器所对应的扰动输入能量的最大值并不相同,且差距很大,没有排除控制频域范围外其他因素的干扰,因此控制效果的对比不够科学。若设置ε=γ2,应用文中方法求解时又会出现没有可行解的问题。王刚等[14]针对该问题提出了引入松弛变量的方法,可通过引入5个松弛变量来减小设计的保守性。这种方法的不足之处在于引入的参数变量较多,且变量的取值更多的需要依赖个人的经验。针对以上问题,本文提出了一种改进的有限频域H∞控制方法,所需的参数更少,并根据悬架可控制的实际频域范围,将全频域控制定义为一种可控频域范围内的有限频域控制,排除了其他因素的干扰,使两种控制效果的对比更加科学。
1 问题描述
考虑如下的线性时间连续系统
(1)
式中:x(t)为系统的状态变量,u(t)为系统的控制输入,w(t)为外界的扰动输入,z1(t)为系统的目标输出,z2(t)为系统的约束输出,A为系统矩阵,B为控制力位置矩阵,D为干扰矩阵,C1、C2为输出矩阵,D1、D2为传递矩阵。
控制器设计的目标就是要设计一个状态反馈控制器u(t)=Kx(t),K为待求的状态反馈增益矩阵。使得系统满足
① 无外界扰动时渐进稳定;
② 在零初始条件下,外界扰动到系统目标输出的传递函数Gwz1(jω)在频域[ω1,ω2]内最小;
③ 外界扰动能量小于wmax∈L2[0,∞)时,控制约束条件始终能够得到保证。
即求解minγ, s.t.
(2)
{z2}i<1,i=1,2,…
(3)
将u(t)=Kx(t)代入式(1)可得
(4)
令A1=A+BK,C11=C1+D1K,C21=C2+D2K,则上式可化为
(5)
2 有限频域状态反馈H∞控制器设计
定理1对于给定的正常数γ、ε和ρ,如果存在对称矩阵P,P1>0,Q>0满足
(6)
<0
(7)
(8)
其中ωc=(ω1+ω2)/2,{·}i表示矩阵{·}的第i行,j代表虚数因子,*表示矩阵对应位置矩阵块的共轭转置。则存在一个状态反馈控制器u(t)=Kx(t)使得系统(5):
① 无外界扰动时渐进稳定;

③ 外界扰动能量小于wmax=ρ/ε时,控制约束条件始终能够得到保证。
证明:首先证明系统(5)在没有外界扰动的情况下是渐进稳定的。
根据Schur补引理[15],式(6)可以等价的写为
(9)
进一步可以推出
(10)
由Lyapunov稳定理论可证,系统(5)无外界扰动时渐进稳定。
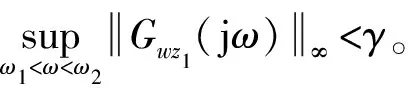
根据Schur补引理,式(7)可以等价的写为
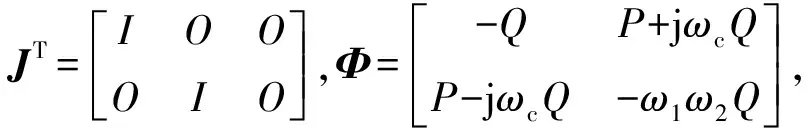
则不等式可等价写为
JΦJT+HΠHT+ΓP1Λ+ΛTP1ΓT<0
根据投影定理[16],上式等价于
(11)
(12)
式中,NΓ和NΛ分别是由核空间Ker(Γ)和Ker(Λ)的任一组基向量作为列向量构成的矩阵。选取
由式(12)又可以进一步可以得到
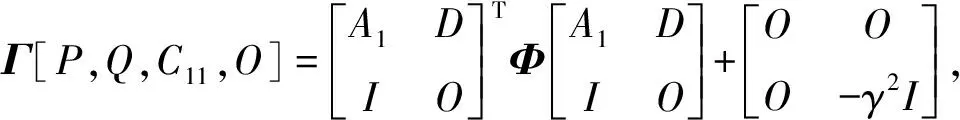
由Schur补引理可得
进一步由GKYP引理推论可以得到
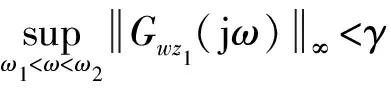
下面对式(8)能够满足控制约束条件进行证明。
由式(10)可知,V(t)=xT(t)P1x(t)是系统的一个Lyapunov函数,对V(t)求导得
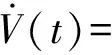
根据基本不等式有
εwT(t)w(t),∀ε>0
进而可得
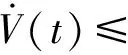
εwT(t)w(t)
不等式两端同时进行0到t的积分可得
V(t)-V(0)≤

式中,系统初始状态为零V(0)=0,wmax为最大的扰动能量。令ρ=εwmax,则进一步可以推出
V(t)=xT(t)P1x(t)≤ρ
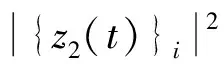
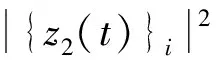
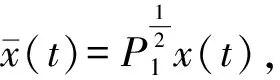
因此
式中,λmax{·}代表矩阵{·}的最大特征值。从而可以看出,如果
成立,则由Schur补引理可知约束条件(8)一定成立,定理1证毕。
考虑到不等式(6)、(7)中含有非线性项,无法利用MATLAB中的LMI工具箱进行计算,此处还需要通过变量代换的方法将其转化为线性矩阵不等式。定义以下对角矩阵
代入A1=A+BK,C11=C1+D1K,C21=C2+D2K,用J1、J2、J3分别左乘和右乘不等式(6)~(8)进行全等变换,并重新定义矩阵变量如下
则矩阵不等式(6)~(8)可化为
(13)
(14)
(15)
注意到矩阵不等式(14)中的矩阵是复矩阵,无法使用MATLAB中的LMI工具箱进行求解,还需要将其转化为实线性矩阵不等式的形式。根据复线性矩阵不等式的处理方法,埃尔米特矩阵M=X+jY<0,当且仅当
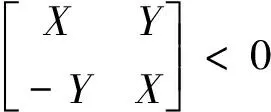
(16)
则可令
综上,可得到能够直接用于求解有限频域状态反馈H∞控制器的定理如下。
定理2对于给定的常数γ、ε和ρ,如果存在对称矩阵满足线性矩阵不等式(13)、(15)、(16),则可以设计一个状态反馈H∞控制器,控制器状态增益矩阵使得系统(5)满足:
① 无外界扰动时渐进稳定;

③ 外界扰动能量小于wmax=ρ/ε时,控制约束条件始终能够得到保证。
应用定理2可将系统有限频域状态反馈H∞控制器的设计,转化为可用MATLAB直接进行求解的如下凸优化问题
minγ, s.t. LMIs(13)、(15)、(16)
此时可计算状态反馈增益
3 车辆主动悬架建模及其控制器设计
以如图1所示的二自由度四分之一车辆主动悬架系统为研究对象,应用定理2提出方法对该系统的有限频域状态反馈H∞控制器进行设计和计算。
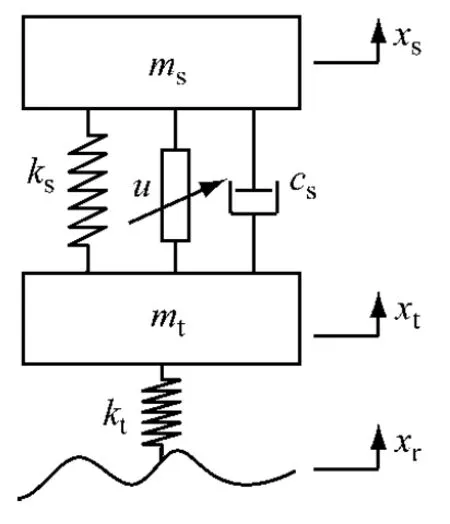
首先建立系统的数学模型,系统在振动过程中的动力学方程为
式中,ms为悬置质量;mt为非悬置质量;ks和kt分别为悬架和车轮刚度;cs为作动器等效阻尼系数;u为主动控制力,对被动悬架而言,u=0;xr为路面不平度位移激励;xs和xt分别为车体和车轮的垂直位移。
对悬架振动的控制目标和约束作如下数学描述:
(1) 控制目标
路面扰动输入为能量有界信号系统控制的目标就是实现有限频域车体加速度对外界扰动的最优抑制,可通过降低路面扰动到车体加速度的传递函数的最大奇异值来实现,这与函数的H∞范数定义相一致,因此控制目标的数学描述就是
(2) 约束条件
控制的约束条件主要包括以下3个方面。
约束条件一:悬架动行程小于其行程最大值;
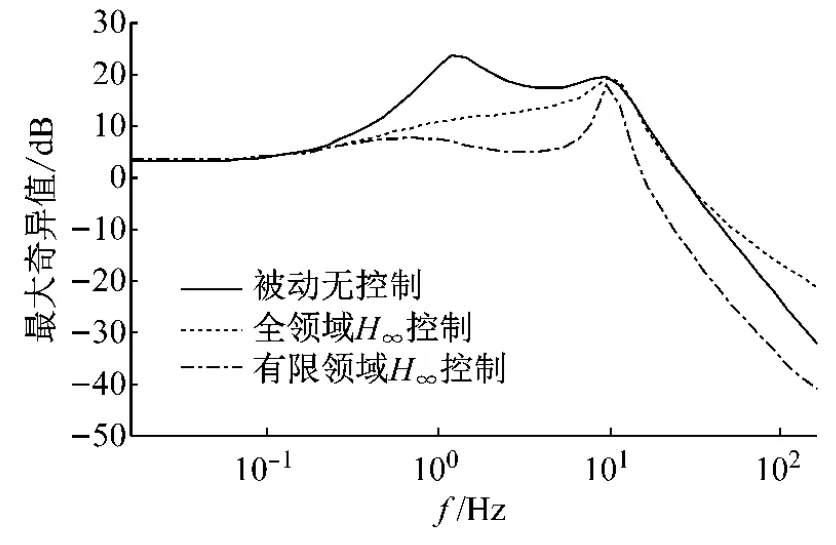
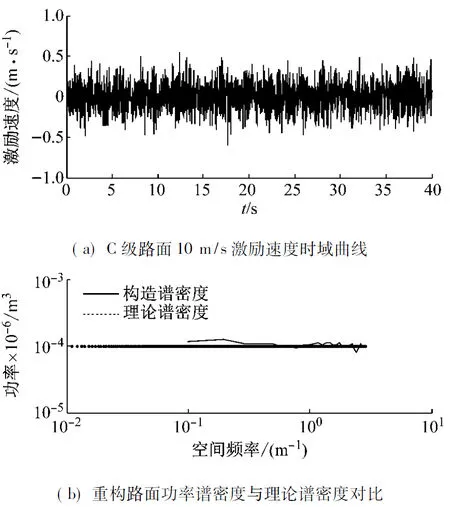
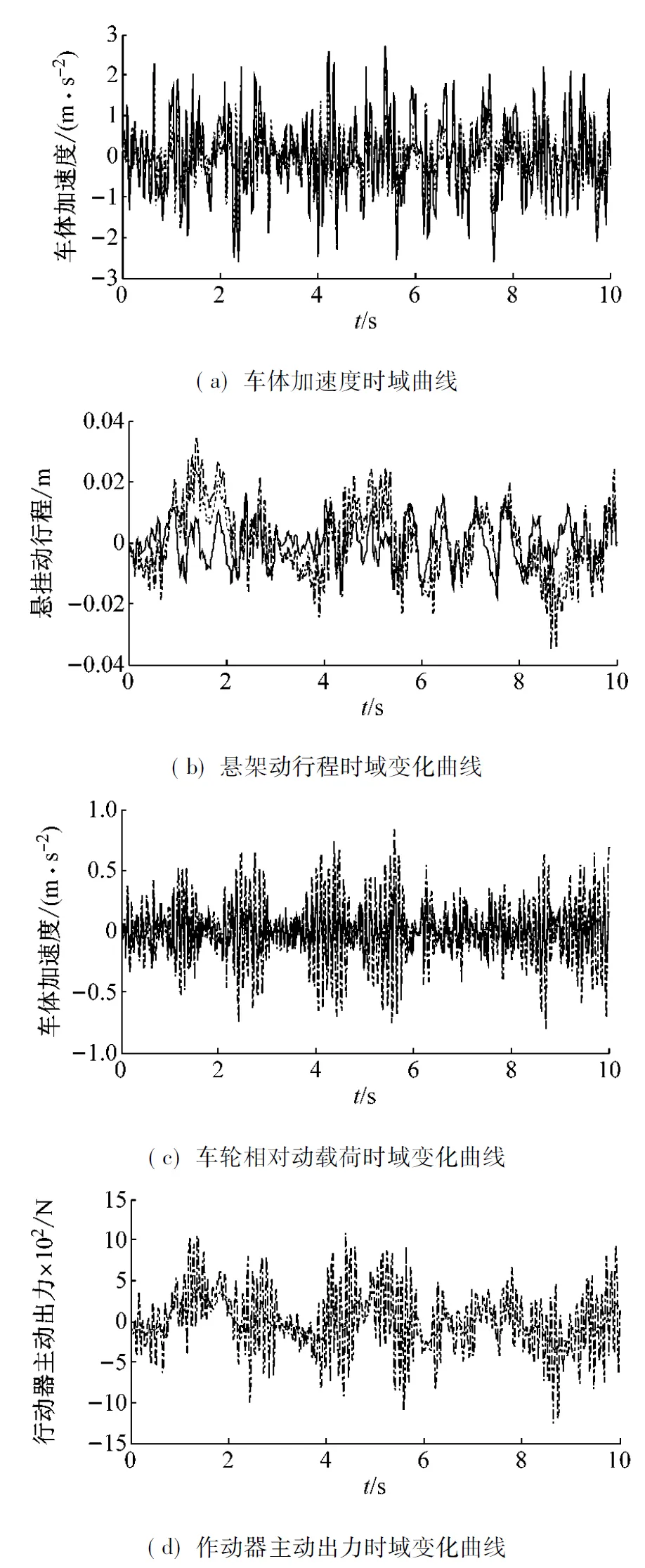
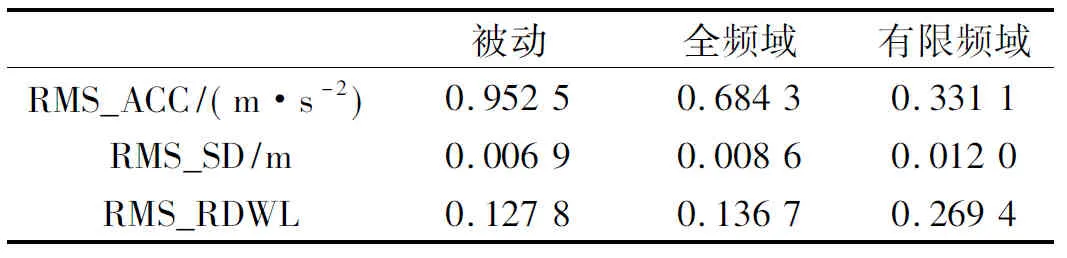
xs(t)-xt(t) 约束条件二:相对动载荷小于1; 约束条件三:控制力小于其最大值。 u(t) 根据以上控制目标和约束条件的描述,可选取系统的状态变量x(t),系统的目标输出z1(t)和约束输出z2(t)分别如下 将悬架系统的运动学方程转化为式(1)所示的状态空间形式,则可得到式中输入、输出变量的系数矩阵 主动悬架参数取值如表1所示,有限频域控制器设计参数取值如表2所示。考虑到车辆悬架的有效控制频域为0.1~30 Hz,为了对比的科学和公平,全频域控制器的设计仍采用定理2的求解方法,但是频域的上下限分别取则可分别求得有限频域状态反馈H∞控制器增益Kf和全频域状态反馈H∞控制器增益Ke如下: Kf=[14 352.14,-1 591.76,-2 091.80,-915.95] Ke=[15 232.85,-1 580.75,26 099.94, 140.97] 利用计算得到的两种控制器增益可分别得到相应的闭环系统最大奇异值曲线,并可与被动无控制条件下的闭环系统进行对比,如图2所示。从图中可以明显的看出,与被动无控制状态相比,两种控制器基本在全频域上都有较好的振动抑制效果;与全频域状态反馈H∞控制相比,改进的有限频域状态反馈H∞控制在人体敏感的4~8 Hz频域范围内有更为优异的振动抑制效果。 为了验证以上理论计算得到的结论,下面采用随机激励作为激励信号源,对控制器的控制性能进行仿真分析。对于随机激励,通常采用位移功率谱密度Gxr(n)来描述路面不平度的统计特性,并把路面划分为A~H的8个等级[17],其拟合表达式为 式中:n表示空间频率,m-1;n0为参考空间频率,取值为0.1 m-1;Gxr(n0)为路面不平度系数,m2/(m-1);w为频率指数,通常取2;nu,nl分别代表上、下限空间频率,通常取值为2.83 m-1、0.011 m-1。 本文中的随机激励采用的是速度输入,当频率指数w=2时,速度功率谱密度与位移功率谱密度之间的关系为 (18) 为了实际仿真的使用,还需要引入车速v,将路面不平的空间功率谱密度转化为时间功率谱密度。设时间频率为f,则 f=nv (19) 根据式(17)~(19)采用谐波叠加法生成一段C级路面10 m/s条件下的一段路面,其时域曲线及功率谱密度曲线分别如图3(a)、(b)所示,从图3(b)中可以看出构造的路面激励速度功率谱密度与理论谱密度能够较好的吻合。 如图4所示为系统在C级路面10 m/s的随机激励条件下输出变量的时域变化曲线。其中图4(a)为车体加速度的时域变化曲线,从图中可以看出,两种控制器的振动抑制能力都要明显优于传统的被动悬架,而有限频域状态反馈H∞控制器比全频域状态反馈H∞控制器的振动抑制能力更强,达到了最优化有限频域控制的目标;图4(b)所示为悬架动行程的时域变化曲线,从图中可以看出,两种控制器的悬架动行程均小于悬架允许的最大行程,满足控制约束条件一的要求;图4(c)所示为车轮相对动载荷的时域变化曲线,从图中可以看出,两种控制器的相对动载荷均小于1,满足控制约束条件二的要求;图4(d)所示为作动器主动出力的时域变化曲线,从图中可以看出,两种控制器的主动出力均小于2 000 N,满足控制约束条件三的要求。 分别对车体加速度均方根值(RMS_ACC)、悬架动行程均方根值(RMS_SD)和车轮相对动载荷均方根值(RMS_RDWL)等悬架系统的输出性能指标进行量化的统计计算,结果如表3所示。从表中数据可以看出,同被动无控制状态相比,全频域和有限频域状态反馈H∞控制下车体加速度均方根值分别降低了28.16%和65.23%,而悬架动行程和车轮相对动载荷虽然都有不同程度的恶化,但是均在许用范围之内。 下面再从频域角度对控制器的控制性能进行分析。如图5所示为车体加速度功率谱密度频域上的变化曲线,从图中可以看出两种控制器在整个频域范围内均有优于传统被动悬架的振动抑制能力,且同全频域状态反馈H∞控制相比,有限频域状态反馈H∞控制在4~8 Hz频域范围内的振动抑制效果要明显优于全频域状态反馈H∞控制的振动抑制效果。对比图2可以发现,这与理论上的分析是一致的。综合以上的时域和频域上的分析我们可以得出结论:新设计的有限频域状态反馈H∞控制器能够实现控制约束条件的情况下,对关注的有限频域范围进行更为有效的振动控制。 以GKYP引理为依据,设计并理论推导了一种改进的有限频域状态反馈H∞控制方法,与其他有限频域控制方法相比,该方法具有所需参数少,基于线性矩阵不等式,便于使用MATLAB的LMI工具箱进行求解的特点。同时,根据悬架可控制的实际频域范围,将全频域控制定义为一种可控频域范围内的有限频域控制,排除了其他因素的干扰,使两种控制效果的对比更加科学。最后利用随机路面激励对设计的控制方法进行了仿真验证,仿真结果表明,相对于传统的被动悬架和全频域状态反馈H∞控制方法,改进的有限频域状态反馈H∞控制能够在保证控制约束条件的情况下更加有效的抑制4~8 Hz频域范围内的振动,改善车辆的乘坐舒适性。4 仿真分析

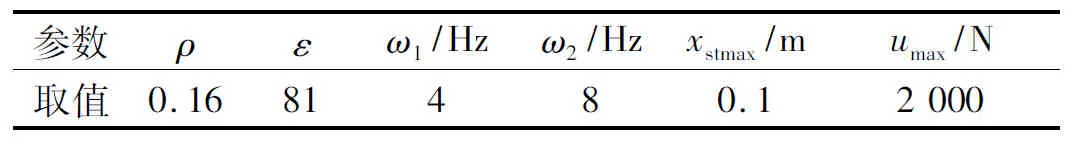

5 结 论

