考虑热效应的滚滑并存线接触粗糙界面的摩擦能量耗散特性研究

肖会芳， 孙韵韵， 陈再刚

(1.北京科技大学 机械工程学院，北京 100083；2.西南交通大学 牵引动力国家重点实验室，成都 610031；3.北京科技大学 钢铁共性技术协同创新中心，北京 100083)

机械设备中，广泛存在着滚滑并存线接触粗糙界面。这类界面的特点是相互接触的表面具有粗糙形貌，在接触区形成线接触，同时存在相对的滑动与滚动，例如轧辊与带钢形成的轧制界面、齿轮的啮合界面、滚动轴承的滚动体-滚道界面等[1-3]。

随着机械设备的高速、重载化，机械结构滚滑并存界面的温度热效应变得显著，引起润滑液性能、界面油膜厚度和摩擦能量耗散量等界面属性发生变化。机械结构界面的摩擦耗散性能直接影响界面的刚度和阻尼等动力学特性参数，可导致机械结构的动力学特性、磨损特性和工作稳定性等发生根本性变化[4-8]。

关于润滑接触界面的弹流润滑模型和润滑性能研究，获得了广泛的关注。例如，邓玫等[9]考虑表面形貌、热效应和轴承表面变形等因素，研究了轴变形导致轴颈在轴承中倾斜时，滑动轴承的热弹性流体动力润滑性能。结果表明，表面热变形对轴承性能的影响程度与转速高低和轴承载荷直接相关。卢宪玖等[10]假设轴承滚道和滚动体表面粗糙形貌为余弦函数，建立角接触球轴承的热弹流润滑模型，研究了表面粗糙度对压力和膜厚的影响。陈园等[11]考虑热效应对润滑流体的黏度、密度和比热容的影响，研究了高转速下润滑流体特性对静压滑动轴承润滑性能的影响。Ghahnavieh等[12]采用背锥近似法将直齿锥齿轮轮齿接触等效为多对直齿轮轮齿接触，研究了载荷、表面粗糙度、硬度和滚动速度等对直齿锥齿轮轮齿界面的油膜厚度和摩擦因数的影响特性。结果显示，当表面粗糙度大于0.5 μm时可引起润滑状态从液压润滑转变为混合润滑状态。Habchi[13]对含有涂层的接触界面进行了热弹力学分析，研究了表面涂层的热力学特性对接触界面摩擦的影响特性。结果显示，低热惯量的涂层能够降低界面摩擦。Linjamaa等[14]考虑轴承表面和聚合物内衬的弹性变形和热变形，提出了参数化数值计算模型，研究含有聚合物内衬的水动力径向滑动轴承的压力、液体厚度等参数的变化特性。

上述研究通过建立纯滑动接触界面、点接触界面或纯滚动接触界面的弹流润滑模型，研究了表面形貌、温度热效应、速度等对界面润滑和摩擦等性能的影响特性。但是，针对机械结构中广泛存在的滚滑并存线接触粗糙界面，目前仅考虑纯滑动或纯滚动的润滑模型和获得的计算结果，尚不能用于准确描述界面的流体动力润滑性能，以及界面的摩擦能量耗散性能。

本文通过建立滚滑并存线接触粗糙界面模型，考虑滚滑并存工况条件和界面相对运动引起的温度热效应，建立了滚滑并存线接触粗糙界面的能量方程、油膜厚度方程和粗糙体接触压力方程，求解了界面温度场，研究了表面粗糙形貌、运动速度和法向载荷对界面的油膜厚度和摩擦能量耗散的影响特性。

1 滚滑并存粗糙界面润滑模型

1.1 模型描述

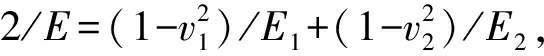
(a) 两圆柱体接触

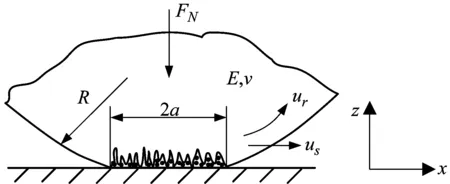
(b) 圆柱体-刚性平面接触等效模型

1.2 载荷分配思想

基于Johnson的载荷比例因子思想，滚滑并存润滑状态下，界面的外部法向载荷FN由油膜压力FH和粗糙峰微凸体接触力FC共同承担[15]

(1)

式中，γ1和γ2分别是润滑油膜和微凸体承受载荷的载荷因子，且有

(2)

假设金属表面的粗糙微凸体对界面油膜的液体动力行为无影响，则界面的摩擦力可以表示为

Ff=Ff,H+Ff,C

(3)

式中，Ff,H是液体动力摩擦力，Ff,C是粗糙微凸体接触摩擦力。

1.3 摩擦能量耗散量

假设界面的不同微凸体均具有相同的库仑摩擦因数[16]，界面的微凸体摩擦力Ff,C可以表示

(4)

式中，fc为界面的平均粗糙体摩擦因数，其值通过实验测试确定。

考虑界面相对运动引起的温度热效应，对牛顿润滑液，假设整个接触区油膜厚度等于接触中心油膜厚度，界面的液体动力摩擦力可表示为[17]

(5)

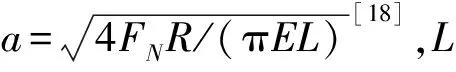
η(FN,T)=η0exp (lnη0+9.67)×

(6)

(7)

式中，α为压力-黏度系数。

单位时间内界面的摩擦能量耗散量可以表示为

(8)

式(8)显示，界面摩擦能量耗散量由两部分组成，一部分是粗糙微凸体接触摩擦耗散Eff，另一部分是液体动力摩擦耗散EfH，是工作温度下的动力黏度η、滑动速度us、法向载荷FN、油膜厚度hcT和粗糙微凸体载荷比例因子γ2的函数。

2 考虑温度热效应的滚滑并存粗糙界面动力方程

2.1 界面温度场

混合润滑状态下，界面的热效应由油膜的剪切流变和粗糙微凸体的摩擦滑动产生。考虑表面粗糙度的影响，假设沿油膜厚度方向的黏性耗散相同且滚动速度的变化符合Couette流动，并忽略压缩、对流、测流的影响，线接触弹流动力润滑的能量方程可以表示为

(9)

式中，Kf为润滑液的热传导系数，pc为微凸体中心接触压力，h为油膜厚度。边界条件为

z=0,T=T1(x);z=h,T=T2(x)

(10)

式中，T1(x)和T2(x)为沿滑动方向接触体表面的温度分布。对式(9)积分并代入式(10)的边界条件，油膜厚度方向的温度可以表示为

(11)

表面温度为

(12)

(13)

式中，ρ1和ρ2,Cp1和Cp2,K1和K2,ur1和ur2分别为接触表面的密度、比热、热传导系数和滚动速度，xin为油膜入口位置。引入热通量q和热量分配因子Ch(x)，传递到上表面的热量为q[1-Ch(x)]，传递到下表面的热量为qCh(x)，且有

(14)

(15)

联合式 (14) 和 (15) ，可以得到热通量和表面温度差的表达式为

(16)

(17)

将式(16)代入式(12)和式(13)，表面温度分布与热通量的关系可以表示为

(18)

(19)

联立式(17), 式(18)和式(19), 求解获得热量分配因子

(20)

其中

温度T1和T2之间的关系还可以表示为

(21)

联合式(17)和式(21)，求解获得表面温度为

T1(x)=T0+

(22)

(23)

则接触区润滑油膜的温度可以表示为

(24)

式(24)显示滚滑并存润滑条件下，润滑油膜的温度是接触体表面平均温度与由界面相对滑动引起的温升之和。对图1(b)所示模型，α1=0，T1(x)=T0，xin=-a,则式(24)可表示为

(25)

润滑油膜的平均温度为

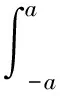
(26)

2.2 考虑温度热效应的流体弹性动力

等温条件下，考虑界面的表面粗糙形貌，基于Johnson的载荷分配思想，粗糙界面线接触区的油膜厚度可表示为[19]

(27)

其中

各无量纲参数分别为

HRI=3M-1,HEI=2.621M-1/5,HRP=1.287Q2/3

式(27)所示的油膜厚度计算基于入口油膜温度。为了考虑由于油膜剪切流变特性和粗糙微凸体相对滑动引起的热效应对油膜厚度的影响，引入热降系数Ct，定义为热油膜厚度和等温油膜厚度的比值[20]

(28)

式中，G是无量纲材料参数，W是无量纲载荷，Sr是滑滚率，γ是润滑液的温度-黏度因子。考虑温度热效应后的油膜厚度为

hcT=Cthc

(29)

2.3 粗糙微凸体接触力

采用Greenwood-Williamson统计模型(GW模型)描述界面粗糙形貌，基于Johnson的载荷分配思想，考虑界面温度热效应，界面粗糙微凸体的接触压力为[21]

(30)

式中，n为微凸体的密度，β为微凸体的平均半径，σs为微凸体高度的标准偏差，dd为粗糙峰平均平面与粗糙面高度平均平面之间的距离，dd=1.15σs，且

同时，混合润滑状态下，微凸体接触的中心压力可以表示为[22]

(31)

式中，a1=1.558,a2=0.033 7,a3=-0.442,a4=-1.70。式(29)与式(30)相等，采用E/γ2代替式(30)中的E，FN/γ2代替式(30)中的FN，nγ2代替n，并无量纲化,则有

(32)

各无量纲参数为

联立式(2)，式(27)，式(28)，式(29)和式(32)，可以求解未知参数hcT，γ1和γ2。对式(30)和式(32)中的积分F3/2，在MATLAB中利用数值积分函数Quadgk获得其数值解。将hcT代入式(26)并联立式(6)，可以求解油膜平均温度T和动力黏度η。将η，hcT和γ2代入式(8)，即可确定摩擦能量耗散量。

3 模型有效性验证

为了验证本文考虑温度热效应的滚滑并存粗糙界面润滑模型的有效性，将模型仿真计算获得的摩擦因数-滚滑率关系曲线与文献[23]中双滚子的实验测试结果进行对比，摩擦因数f=Ff/FN。实验测试时，滚子的速度非常低以尽量减小流体动力效应而获得不同粗糙表面的摩擦因数随滚滑率的变化关系。实验中，微凸体高度标准差分别为σs=0.283 μm和σs=0.465 μm，法向载荷FN=1 988 N。其他实验参数如表1所示。模型计算获得的摩擦因数随滑滚率Sr变化关系与实验测试结果的对比图，如图2所示。图2显示，模型的计算结果与实验测试结果基本一致，表明本文的考虑界面热效应的滚滑并存粗糙界面润滑模型是可靠的。图2同时显示，由于界面的流体动力效应很弱，由流体动力效应引起的流体摩擦很小，界面的摩擦主要来自于粗糙微凸体接触摩擦，因而随着滚滑率增大，摩擦因数的变化很小。

图2 模型计算结果与实验测试结果对比

4 计算结果与分析

采用滑滚率Sr描述界面间的相对运动，对不同粗糙度的界面，包括光滑界面、中等粗糙界面、粗糙界面，改变界面的运行工况参数，包括滑滚率Sr和法向载荷FN，获得不同运行工况时，不同粗糙度界面的油膜厚度参数λ和摩擦能量耗散量Ef的变化关系曲线。不同粗糙度界面的表面形貌参数，如表2所示。其中，光滑表面的表面高度分布标准偏差σ=0.08 μm，对应的粗糙度值Ra=σ/1.1=0.073 μm；中等粗糙表面的表面高度分布标准偏差σ=0.3 μm，对应的粗糙度值Ra=0.27 μm；粗糙表面的表面高度分布标准偏差σ=1 μm，对应的粗糙度值Ra=0.9 μm。计算采用的参数初始值，如表3所示。

法向载荷不同时，油膜平均温度随滑滚率的变化关系曲线，如图3所示。图3显示，随着滑滚率增大，油膜温度升高，且升高的速率随滑滚率的增大急剧增加。随着法向载荷增加，油膜温升更高，界面热效应更显著。

图3 不同法向载荷时，油膜温度沿滑滚率的变化关系曲线

法向载荷不同时，热降系数Ct随滑滚率的变化关系曲线，如图4所示。图4显示，热降系数Ct<1，且随着滑滚率增大而减小，即考虑温度热效应后的油膜厚度hcT小于等温油膜厚度hc。随着法向载荷增加，界面热效应更显著，对应的热降系数减小。

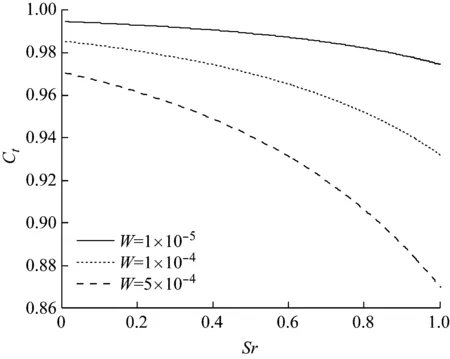
图4 不同法向载荷时，热降系数随滑滚率的变化关系曲线

4.1 油膜厚度参数变化特性

界面等温和考虑界面温度热效应情况下，具有不同粗糙度界面的油膜厚度参数λ随滑滚率的变化关系曲线，如图5所示。无量纲载荷W=2.2×10-4。其中，图5(a)为光滑表面，图5(b)为中等粗糙表面，图5(c)为粗糙表面。油膜厚度参数定义为油膜厚度与表面粗糙度之比，即λ=hcT/σs，用于确定表面的润滑状态。通常，λ<3对应于边界润滑状态，1<λ<3对应于混合润滑状态，λ>3对应于液压润滑状态。图5显示，对不同粗糙度界面，油膜厚度参数随着滑滚率增加逐渐增大，即界面的油膜厚度不断增大；相同滑滚率条件下，随着表面粗糙度增大，油膜厚度参数递减。对光滑表面，随着滑滚率增加，油膜厚度参数从λ<3增大到λ>3，界面的润滑状态从混合润滑过渡为液压润滑。对中等粗糙表面和粗糙表面，油膜厚度参数λ<1，界面的润滑状态为边界润滑。图5同时显示，与不考虑界面热效应(等温)相比，考虑界面热效应时，油膜厚度参数减小，即界面油膜厚度减小，界面达到液压润滑状态所需的滑滚率增大，且温度热效应对油膜厚度参数的影响随着滑滚率的增加更加显著。

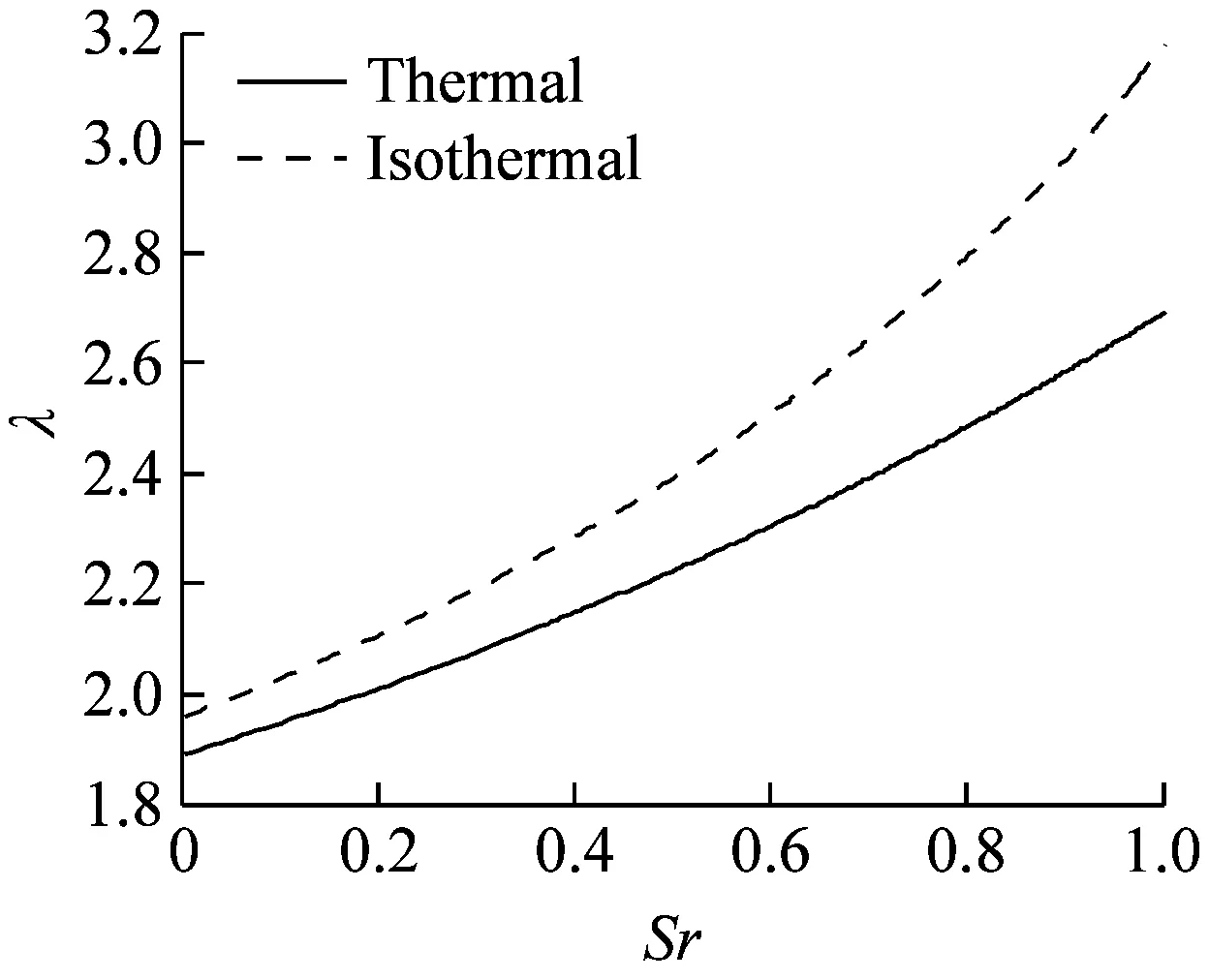
(a) 光滑表面

(b) 中等粗糙表面

(c) 粗糙表面

界面等温和考虑界面温度热效应情况下，具有不同粗糙度界面的油膜厚度参数λ随无量纲法向载荷的变化关系曲线，如图6所示。滑滚率Sr=0.6。其中，图6(a)为光滑表面，图6(b)为中等粗糙表面，图6(c)为粗糙表面。图6显示，对不同粗糙度界面，油膜厚度参数均随着法向载荷增加而递减，即界面的油膜厚度随着法向载荷增加不断减小，且呈现先剧烈后缓慢的变化趋势。当法向载荷较小时，即轻载条件下，随着载荷增加，油膜厚度参数急剧减小，且减小的剧烈程度随表面粗糙度增大而增大；当法向载荷较大时，即重载条件下，随着载荷增大，油膜厚度参数缓慢减小，尤其是对粗糙表面。

图6同时显示，与不考虑界面热效应(等温)相比，考虑界面热效应时，相同载荷时的油膜厚度参数减小，且温度热效应的影响随着载荷的增大更加显著。但是，随着表面粗糙度增大，温度热效应对油膜厚度-载荷关系曲线的影响逐渐减小；对粗糙表面，温度热效应的影响很小，几乎可以忽略不计。

(a) 光滑表面

(b) 中等粗糙表面

(c) 粗糙表面

4.2 摩擦能量耗散量变化特性

界面等温和考虑界面温度热效应情况下，具有不同粗糙度界面的摩擦能量耗散量随滑滚率的变化关系曲线，如图7所示。无量纲载荷W=2.2×10-4。其中，图7(a)为光滑表面，图7(b)为中等粗糙表面，图7(c)为粗糙表面。

图7显示，滑滚率较小时，由于温度热效应并不显著，等温条件的界面摩擦能量耗散量与考虑界面热效应的摩擦能量耗散量差异较小。随着滑滚率增大，温度热效应变得显著，等温情况下的界面摩擦能量耗散量更大，且随滑滚率呈非线性递增。而考虑温度热效应时，摩擦能量耗散量随滑滚率先增大后减小，存在最大值。这是由于与等温条件相比，热效应使得润滑液动力黏度η和油膜厚度hcT均减小。在滑滚率较小时，温度热效应不显著，动力黏度η的减小量较小，而油膜厚度的减小量较大，液体动力摩擦耗散量递增；随着滑滚率增大，温度热效应变得显著，动力黏度η的减小量增大，其对液体动力摩擦耗散量的减小作用增大，引起液体动力摩擦耗散量反而减小。

图7同时显示，随着表面粗糙度增大，界面总的摩擦能量耗散量逐渐减小。对光滑表面，界面工作在液压润滑状态，界面的摩擦能量耗散量Ef几乎完全来自于液体动力摩擦耗散EfH，如图7(a)所示。随着表面粗糙度增大，界面工作在混合润滑或边界润滑状态，液体动力摩擦的耗散量EfH逐渐减小，粗糙微凸体接触摩擦耗散Eff逐渐增大，如图7(b)和7(c)所示。

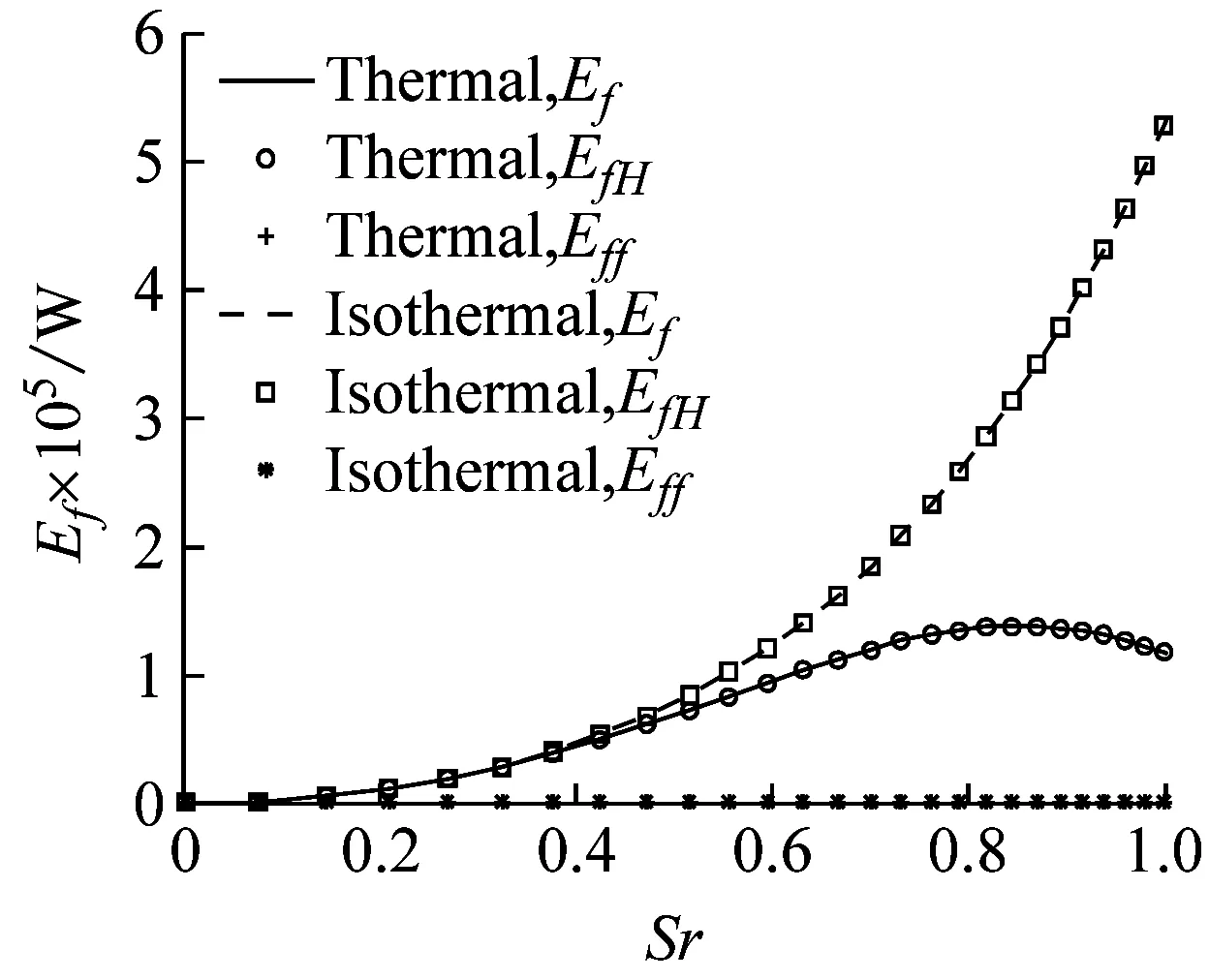
(a) 光滑表面

(b) 中等粗糙表面

(c) 粗糙表面

界面等温和考虑界面温度热效应情况下，具有不同粗糙度界面的摩擦能量耗散量随无量纲法向载荷的变化关系曲线，如图8所示。其中，图8(a)为光滑表面，图8(b)为中等粗糙表面，图8(c)为粗糙表面。摩擦能量耗散量Ef与法向载荷FN之间的关系，如式(8)所示，无量纲法向载荷W与法向载荷FN之间的关系式为W=FN/ERL。图8显示，随着法向载荷增加，摩擦能量耗散量逐渐增大。载荷较小时(轻载)，等温条件下的界面摩擦能量耗散量与考虑界面热效应的摩擦能量耗散量差异较小；随着载荷逐渐增大(重载)，温度热效应变得显著，考虑热效应的界面摩擦能量耗散量更小。这是由于与等温条件相比，温度热效应引起润滑液动力黏度η减小，油膜厚度hcT减小，粗糙微凸体承受的载荷减小，粗糙微凸体接触摩擦能量耗散量和液体动力摩擦能量耗散量均减小，总的摩擦能量耗散量减小。

(a) 光滑表面

(b) 中等粗糙表面

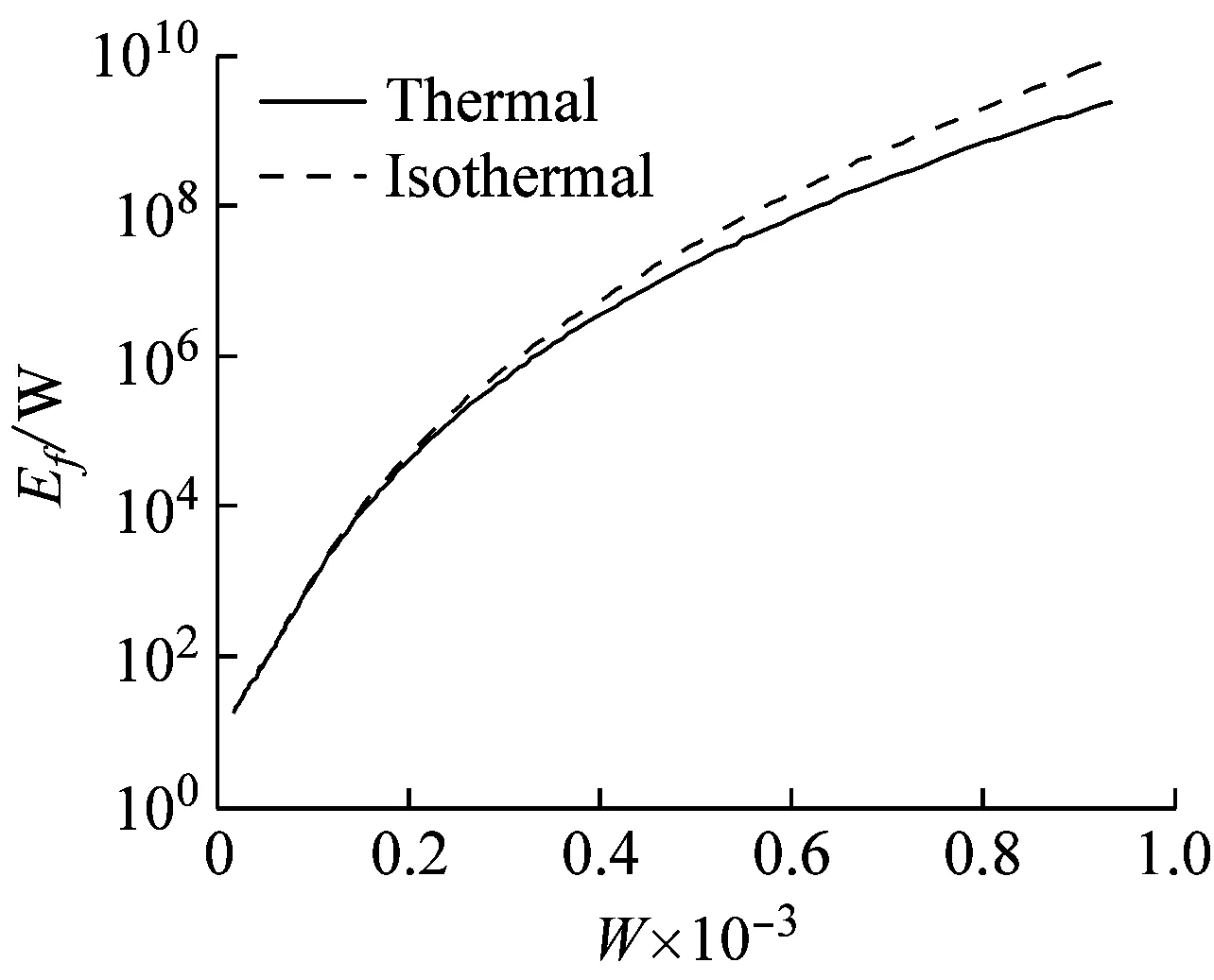
(c) 粗糙表面

考虑温度热效应时，不同粗糙度界面的摩擦能量耗散量，如图9所示。图9显示，当法向载荷较小时，即轻载条件下，表面粗糙度对能量耗散量-载荷关系曲线的影响较大；随着载荷增大，表面粗糙度对能量耗散量-载荷关系曲线的影响几乎可以忽略。这是由于载荷较小时，油膜厚度随载荷变化剧烈，且表面粗糙度对油膜厚度的影响比较显著；载荷较大时，油膜厚度变化缓慢，且粗糙度的影响减弱(图6所示)。

5 结 论

本文考虑温度热效应的影响，建立了滚滑并存粗糙界面润滑模型，基于界面的法向载荷由润滑油膜和粗糙体共同承担的载荷分配思想，研究了表面粗糙形貌、运动速度和法向载荷对界面的油膜厚度和摩擦能量耗散的影响特性，主要结论如下：

图9 考虑温度热效应时，不同粗糙度界面的摩擦能量耗散量

(1) 界面的油膜厚度参数随界面滑滚率增加递增。光滑表面从混合润滑过渡为液压润滑，对中等粗糙表面和粗糙表面，界面的润滑状态为边界润滑；考虑界面热效应时，油膜厚度参数减小，界面达到液压润滑状态所需的滑滚率增大，且温度热效应对油膜厚度参数的影响随着滑滚率的增加更显著。

(2) 界面的油膜厚度参数随法向载荷增加而递减。轻载条件下，油膜厚度参数随载荷增加而急剧减小，且减小的剧烈程度随表面粗糙度增大而增大；重载条件下，油膜厚度参数随载荷增大而缓慢减小。随着表面粗糙度增大，温度热效应对油膜厚度-载荷关系的影响逐渐减小，对粗糙表面，温度热效应的影响几乎可以忽略不计。

(3) 滑滚率较小、轻载条件下，温度热效应对界面摩擦能量耗散量影响较小；随着滑滚率增大、载荷增大，温度热效应变得显著，考虑热效应的界面摩擦能量耗散量更小，且界面摩擦能量耗散量随滑滚率先增大后减小，存在最大值。

(4) 轻载条件下，表面粗糙度对能量耗散量-载荷关系曲线的影响较大；随着载荷增大，表面粗糙度对能量耗散量-载荷关系曲线的影响几乎可以忽略。