基于空间变光滑长度SPH方法研究

施文奎， 沈雁鸣， 陈坚强

(中国空气动力研究与发展中心，四川 绵阳 621000)

SPH方法[1-2]是一种无网格拉格朗日数值方法，在求解模拟多介质、多相、非定常、流固耦合、界面变形和强非线性等问题上具有独特优势。此方法最早用于天体物理领域中，随着方法不断发展和改进，其在流体和固体力学领域应用也越来越广。

在SPH方法中，光滑长度h是非常重要的一个参数，是核函数的重要变量之一，直接影响到求解工程问题时的计算效率和精度。传统SPH方法大多采用恒定一致光滑长度算法[3]，这就限制了整个流场区域的离散粒子为均匀分布模式。伴随着求解问题越来越复杂，其计算域的粒子数需求也越来越大，这导致了计算效率严重下降，计算成本过于巨大。

为提高SPH方法的计算效率及空间分辨能力，需要根据流场区域重要性不同而有针对性地布置粒子分布密度。类似于有限差分法中的网格分布方式，在重点关心区域如冲击位置分布较密粒子，而远离冲击区域分布相对稀疏粒子，并给每个粒子配置独立的光滑长度[4]和质量[5]。

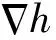
国内这方面的相关研究相对较少，大多集中在应用层面。强洪夫等[12]提出了完全变光滑长度SPH法，并成功应用于高能炸药爆轰过程的模拟。这里提出的方法和文献[8-9]是相似的，区别在于更直接地考虑了变光滑长度的影响以及采用了对称形式的近似核函数。此外苏文周[13]、强洪夫等[14]也基于上述完全变光滑长度方法求解了不同类型的侵彻问题。

以往关于变光滑长度SPH方法的研究大多是为了提高计算精度，因而将粒子光滑长度与密度进行了关联，并随着时间推进而不断改变，且其应用领域也大多集中在天体物理、激波管和爆轰等领域。本文的研究目的是通过设定合适的粒子初始分布，相应地赋予每个粒子独立的光滑长度和质量，并提出适合变光滑长度的链表搜索法，以此提高SPH方法的计算效率和空间分辨力，并将该方法成功应用于模拟气液、液固耦合等典型问题的求解。此方法也可为求解三维入水冲击等复杂工程问题提供技术支撑。

1 空间变光滑长度SPH方法

SPH方法中，对于给定的粒子i，通过应用粒子近似法，粒子i处的函数及其导数的表达式为

Wij=W(xi-xj,h)

(1)

式中，Wij表示相互作用粒子对的光滑核函数，h是定义光滑函数W影响区域的光滑长度，直接影响到计算精度和效率。光滑函数的支持域为x-x′ ≤κh，κ是与点x处光滑函数相关的常数。

1.1 粒子初始参数赋值及作用对称化

当根据计算域的重要程度确定粒子初始分布后，同种类型粒子的密度保持一致，水粒子压力考虑静水平衡后确定，而质量则和粒子所占面积或体积成正比[15]，如图1所示。此外粒子间距Δx是非均匀的，故将每个粒子独立的光滑长度和其自身的Δx比值取为定值，从而保证每个粒子支持域内粒子数量基本不变。此外,为保证支持域内的粒子数量适当，选取光滑长度h=1.23Δx[16]。

图1 质量初始化

当粒子非均匀分布时，粒子i和粒子j光滑长度可能不相等。此时粒子i的影响域可能包含粒子j，但粒子j的影响域则不一定包含粒子i，这不符合牛顿第三定律。因此需要采取特定的处理以保证粒子作用的对称性。

首先在粒子搜索时采用光滑长度的算术平均值来确定相互作用粒子对，即：

(2)

在确定了相互作用粒子对后，将求得的对称光滑长度代入核函数中，即可求得对应的核函数及其导数

Wij=W(rij,hij),

(3)

将求得的核函数及其导数代入SPH方程组中即可得到相应的空间变光滑长度SPH方程组

(4)

SPH方法中很重要的一个性质是将所有流体都考虑为微可压的，即采用如下形式的状态方程[17]

(5)

1.2 链表搜索法

传统链表搜索法是在问题域上铺设一临时均匀网格，网格单元空间大小与支持域大小一致。此时对于给定粒子i而言，其相邻粒子只能在同一网格单元内或者在紧密相邻的单元内，算法的复杂度阶数为O(N)。但当粒子的光滑长度不一致时，如网格单元空间大小与特定粒子i关联的话，则会发生漏掉粒子对的情况。此时链表搜索法必须加入变光滑长度处理。对于密度变化不剧烈如两相流、入水冲击等问题，光滑长度不随时间改变，此时只需将网格单元空间大小与初始最大光滑长度粒子的支持域大小保持一致即可。对于密度变化剧烈如爆炸等问题，光滑长度随时间改变，此时则需要在划分网格前将粒子遍历一遍找到最大光滑长度粒子。

在相同粒子数的情况下，加入变光滑长度处理后的链表搜索法不可避免地会增加搜索时间，但其效率仍比直接搜索法要高很多，且此时其算法的复杂度阶数仍为O(N)。

1.3 粒子扩散分布模型

传统SPH方法大都采用区域一致恒定光滑长度算法，粒子为均匀分布方式。本文采用的是粒子扩散分布模型，在重点关心区域布置较密粒子，而在远离重点区域所布置的粒子逐渐稀疏。气泡上浮算例和楔形体入水冲击算例粒子分布示意图,见图2。

图2 粒子扩散分布模型

气泡上浮算例中，气泡直径为2R，水域大小为10R×6R。此算例中气泡垂直上升，为左右对称算例。气泡上升阶段的形状、位置是我们需要重点关注的信息。故设计粒子初始分布时将计算域分为三部分，中间段(宽为2R)粒子采用传统均匀分布方式，粒子间距Δx/R=0.05。两侧粒子间距从中间开始逐步增大，最大处横向粒子间距为Δx/R=0.144。此时相对全均匀分布模型粒子数减少了约1/4。

非对称楔形体自由入水冲击算例中，冲击载荷峰值、角加速度峰值等是我们重点关心的信息。因此设计粒子初始分布时将水域分为上下两部分(上∶下=1∶2)，上层粒子采用均匀分布，粒子间距为0.005。下层粒子从分界处开始逐步增大，最大处纵向粒子间距为0.015。此时相对全均匀分布模型粒子数减少了约1/4。

2 计算结果及分析

计算中压力P通过采用了人工压缩率的状态方程(式(5)求解，水的声速值取14(gR)0.5。核函数采用Gussian核函数。时间推进采用Leap-Frog格式，边界处理采用Liu等[18]提出的第一类粒子模型。下面通过气泡上浮和楔形体入水冲击算例，主要展示粒子扩散分布模型对计算效率的改进效果，并分析了空间变光滑长度算法对由粒子非均匀分布引起的不稳定性的抑制作用。

2.1 二维气泡上浮

气泡上浮是一种典型的气液两相自由表面流动。圆形气泡在浮力作用下逐渐上浮，伴随着气泡变形甚至破裂。过程中压差阻力、表面张力作用较为复杂。选取的计算模型见图3，初始时刻，气泡半径R为0.3 m的气泡，位于宽为6R，高为10R的水域中。水与空气密度比为：ρX∶ρY=1 000∶1。

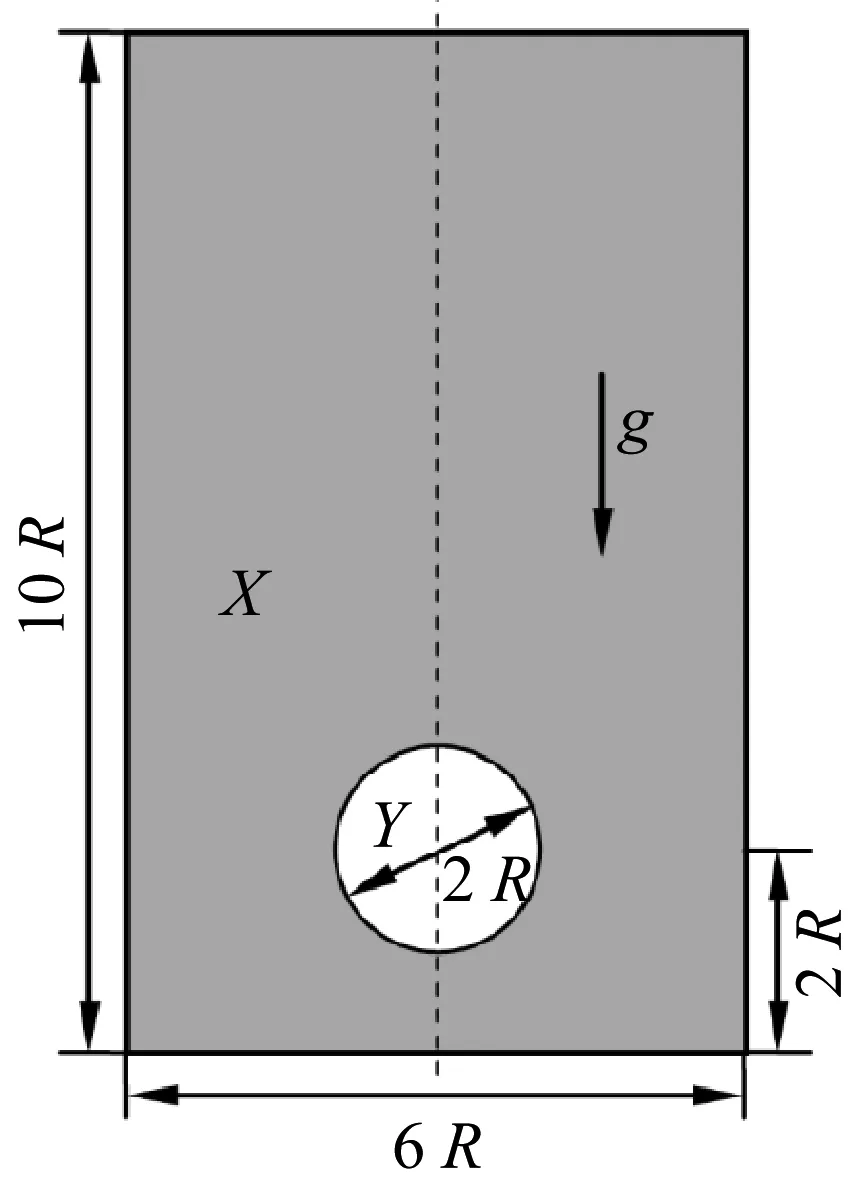
图3 二维气泡上浮模型

首先采用传统SPH方法对均匀粒子分布模型进行模拟，此时粒子间距均为Δx=0.05R，光滑长度为h=1.23Δx，粒子总数为24 940个。时间步长取5×10-6s，采用4核并行计算。同时为保证交界面处的压力匹配，状态方程中γX=7，γY=1.4，且取水的声速值为cX/(gR)1/2=14，空气的声速值为cY/(gR)1/2=198。XSPH方法中的参数ε取为0.1，表面张力项采用文献[19]中给出的形式。图 4给出了计算结果与Level-Set计算结果[20]的比较。可以看出，气泡形状和位置在不同时刻都吻合得较好，验证了程序模拟气液两相流动的有效性。

在此基础上，为提高计算效率，采用粒子扩散分布模型(图 2(a))。此时粒子数为19 120个，粒子数减少了约1/4。其它计算参数选择和上面一致。图5展示了采用粒子扩散分布模型时空间变光滑长度算法对结果的改进效果。三角形的点是图4中传统SPH方法计算得到的结果。圆圈的点是利用粒子扩散分布模型恒定光滑长度算法计算得到的结果，效果很差。正方形的点是扩散分布模型空间变光滑长度算法计算得到的结果，可以看出气泡位置和形态都与粒子均匀分布模型计算得到的结果吻合得很好。

表1给出了粒子均匀分布模型和粒子扩散分布模型计算效率的比较。为避免多核并行带来的干扰，这里采用单核进行测试。此外由于不同粒子搜索方法对于效率的对比会产生很大的偏差，因此这里的计算时间不包括粒子搜索时间。结果表明，计算时间节约1/4左右，大幅提高了计算效率。

2.2 楔形体入水冲击

楔形体入水冲击是一种典型的流固耦合问题。带初始倾斜角的入水冲击问题耦合了大变形、多自由度等现象，其模拟难度更大。选取的计算模型及相关参数见图6，更详细的楔形体实验参数可参考文献[21]。本算例中，水域大小设为长×高=3.6 m×1.8 m。

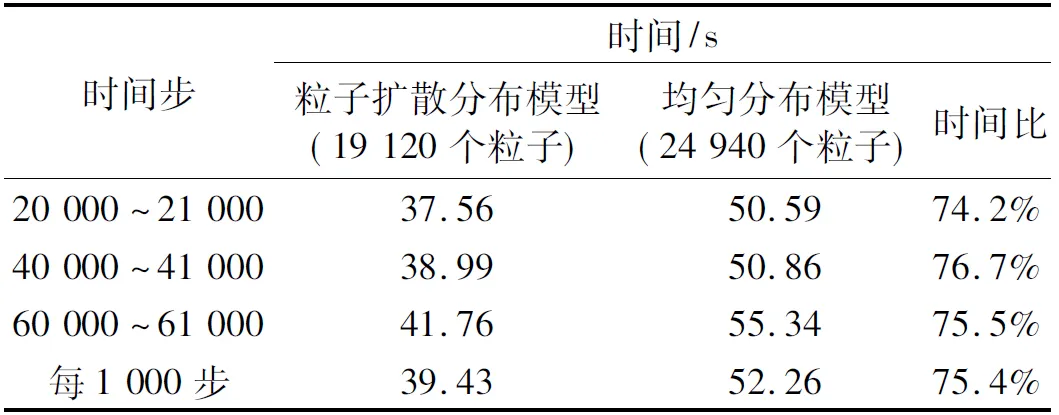
表1 不同粒子分布模型计算时间比较(不包含搜索时间)

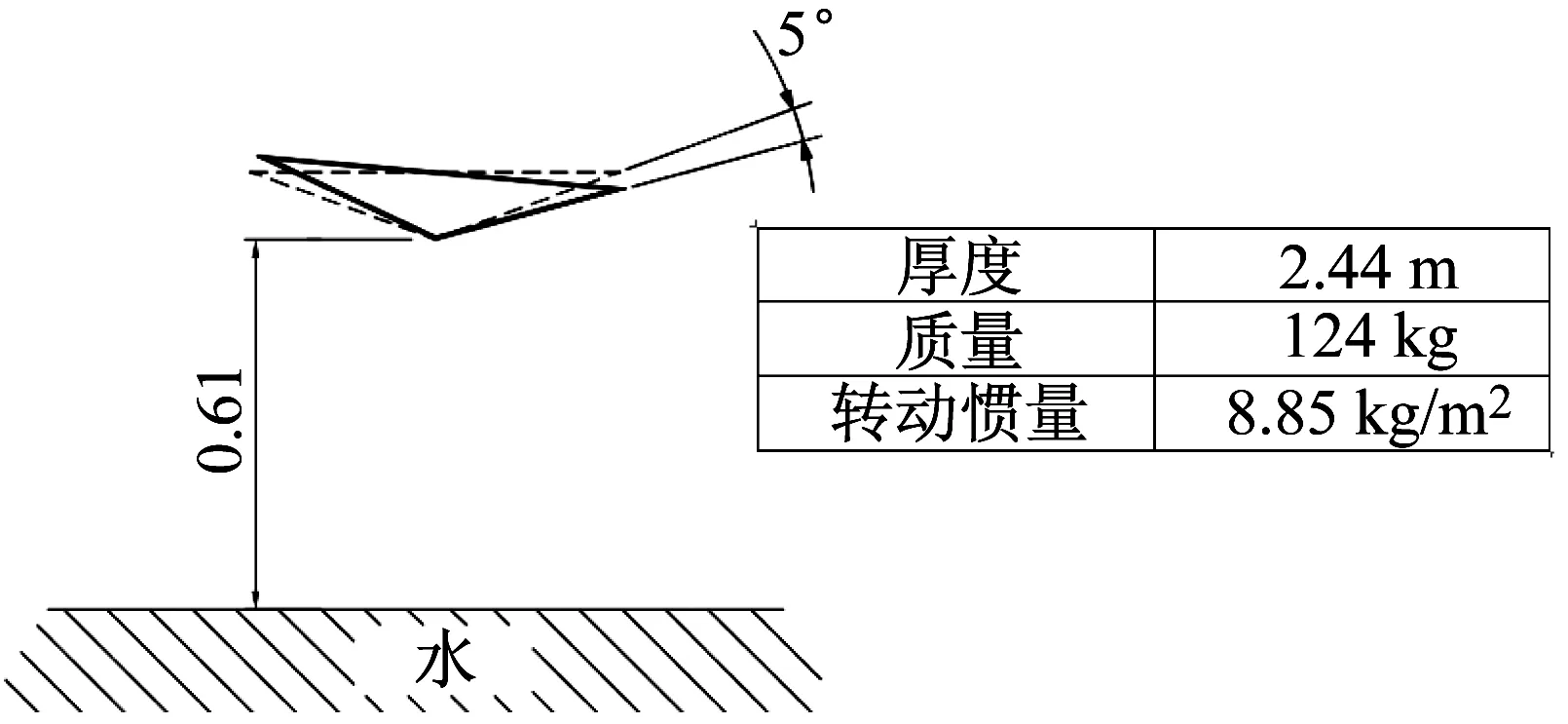
图6 实验参数描述

首先采用传统SPH方法对粒子均匀分布模型进行模拟，此时粒子间距均为0.005，光滑长度均为h=1.23Δx，粒子总数为265 277个。时间步长取10-5s，采用4核并行计算。状态方程中水的声速值取14(gH)0.5,H为水深1.8 m。固壁边界压力采用SPH粒子近似法得到，流固耦合模块计算采用文献[22]中的方法。在上述参数基础上，首先进行了粒子无关性(图7)和时间无关性验证(图8)，结果表明粒子间距和时间步长的选取是有效的。图9给出了垂向加速度、角加速度和楔形体速度计算结果与实验数据对比图。由图可得，程序对流固耦合和液面变形的模拟是有效的。

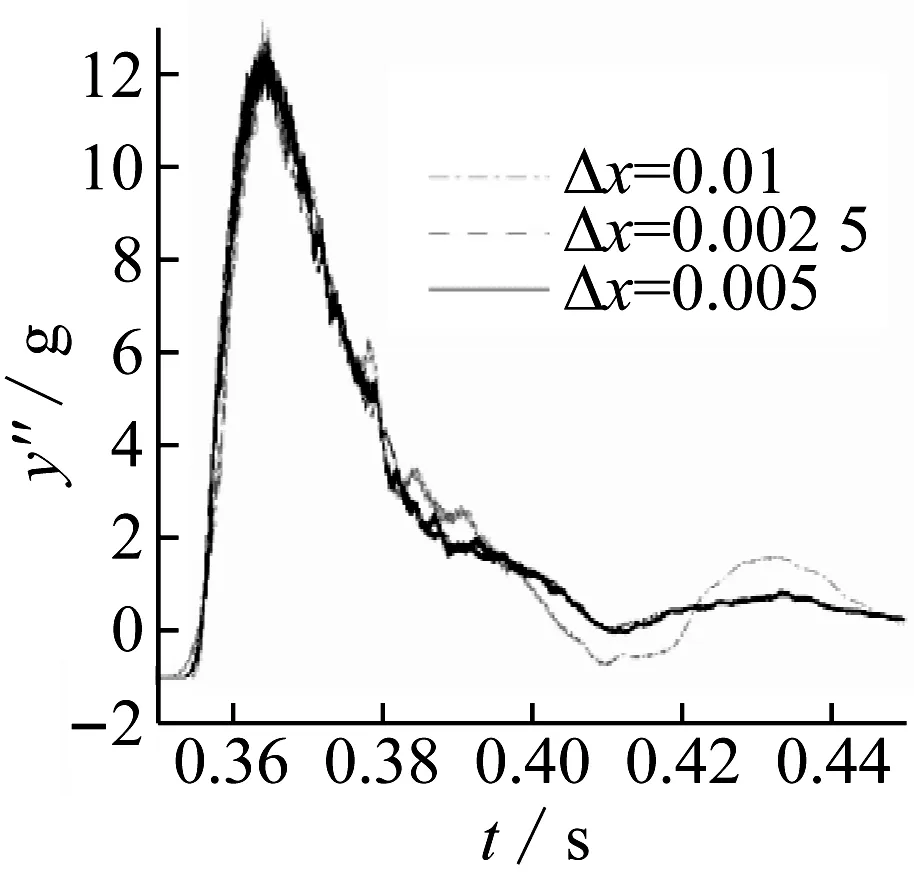
图7 粒子无关性验证Fig.7 Particle independence verification

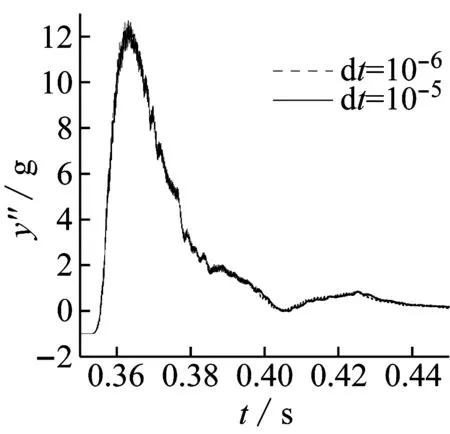
图8 时间无关性验证Fig.8 Time independent verification

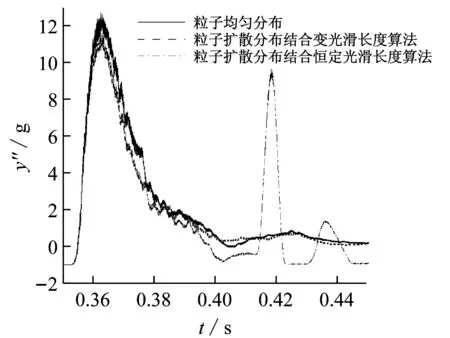
在此基础上，为提高效率，采用粒子扩散分布模型，见图 2(b)。此时粒子数为199 029个，粒子数减少了约1/4，时间步长仍取10-5s。图10给出了采用粒子扩散分布模型时恒定光滑长度算法和空间变光滑长度算法的结果对比。由图可得恒定光滑长度算法得到的计算结果较差，这是由于粒子非均匀分布导致强不稳定性造成的。但当采用了空间变光滑长度技术后，首先其加速度和角加速度与均匀分布粒子模型计算结果吻合得都很好；其次其流场紊乱程度降低降慢(图11)。这一方面是给每个粒子单独配置光滑长度后，其支持域内的粒子数量能够保证基本一致；另一方面则是实现了粒子相互作用对称化，保证了牛顿第三定律。

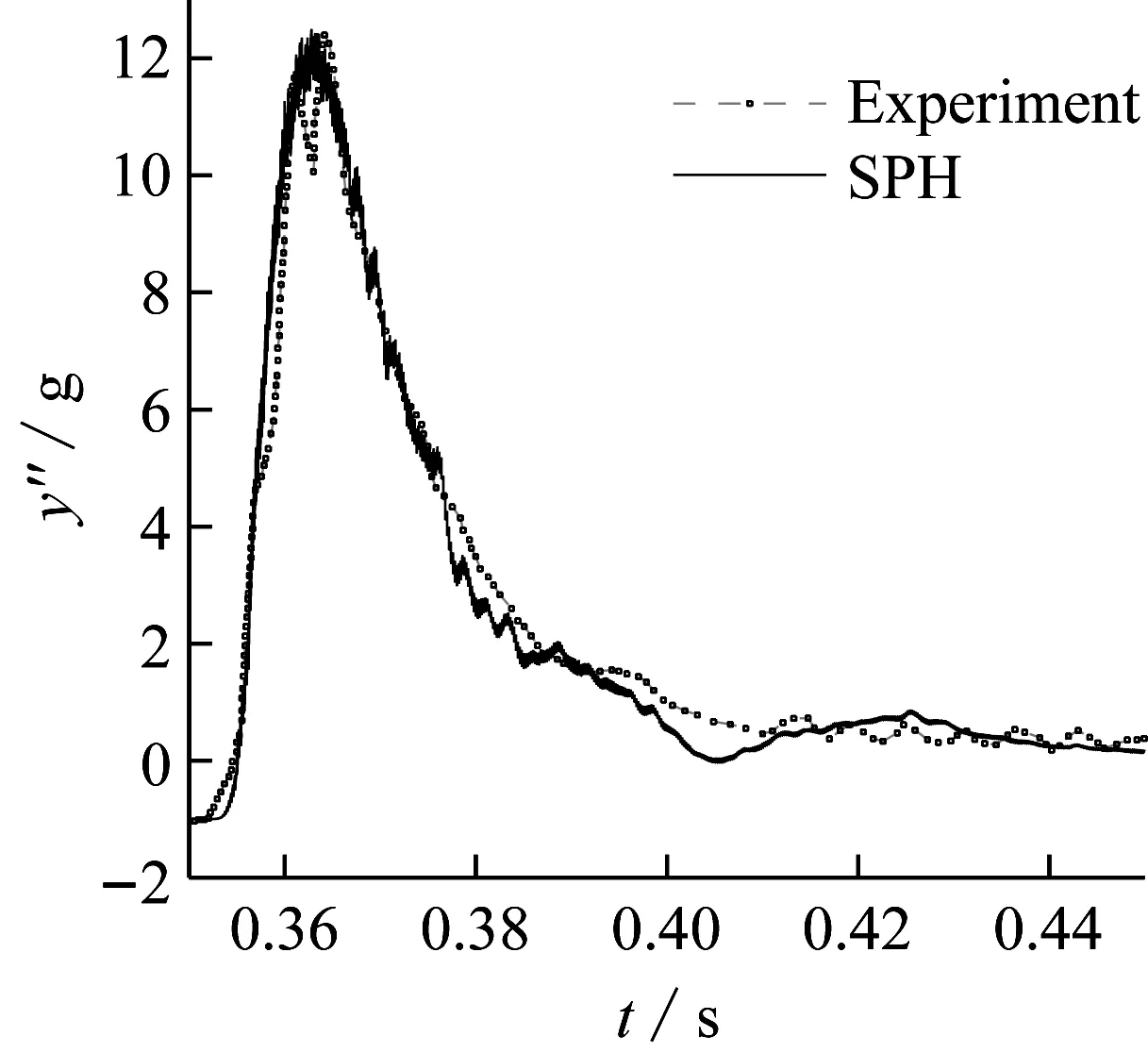
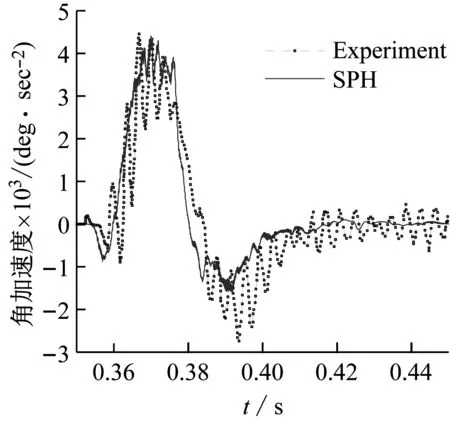
图9 垂向加速度、角加速度、速度验证

(a) 垂向加速度

(b) 角加速度

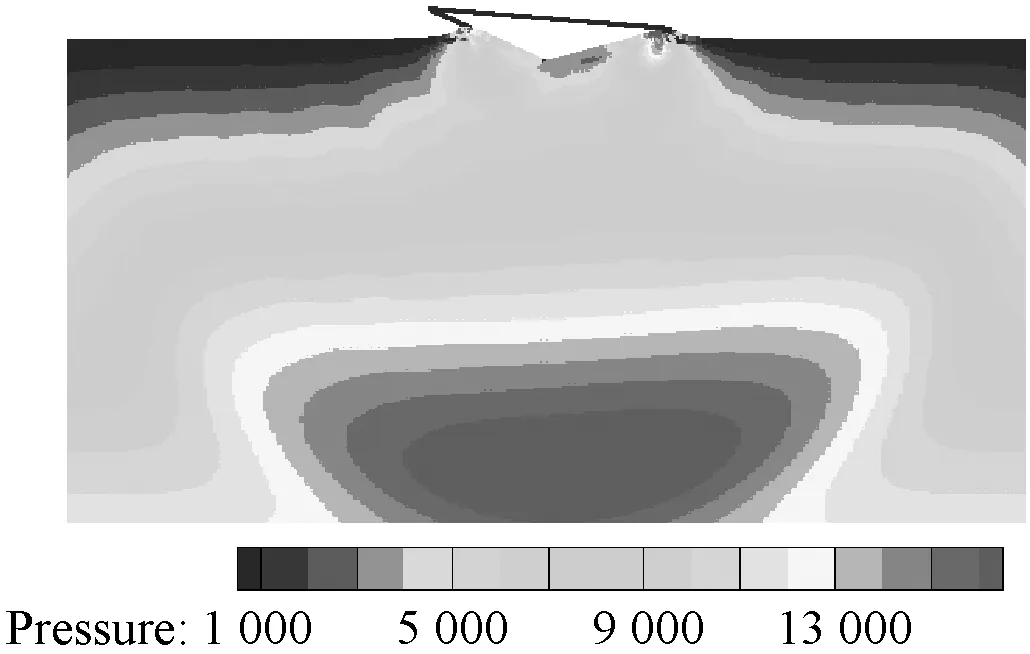
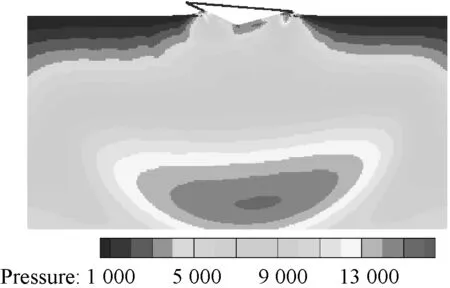
(a) t=0.377 s(左、中和右分别为均匀模型，非均匀变h，非均匀恒定h)

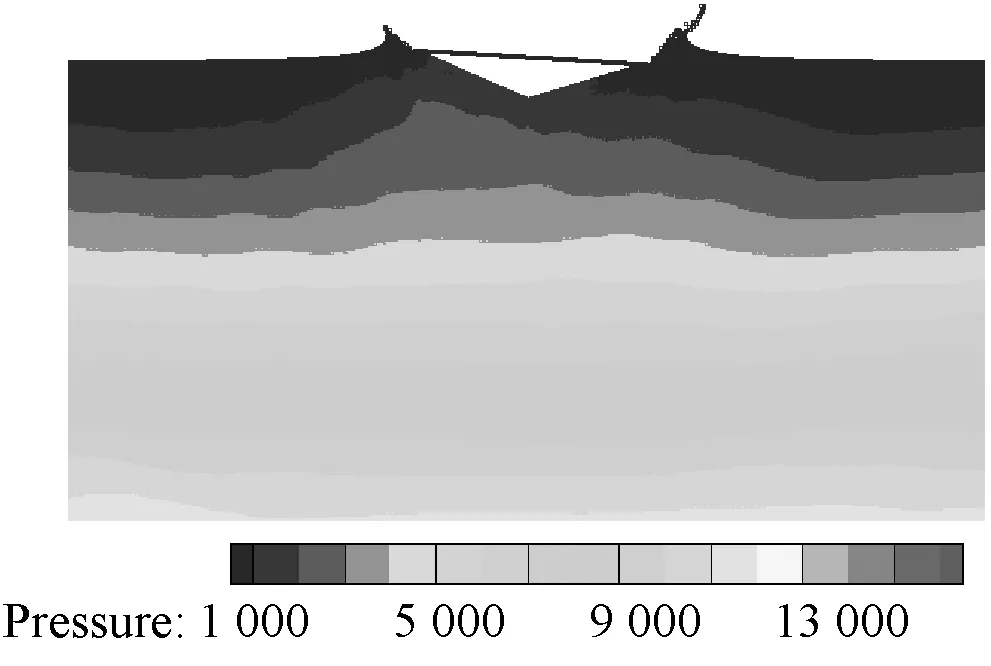
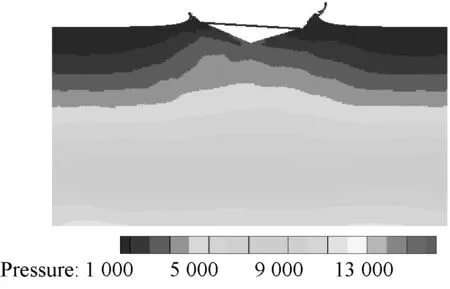
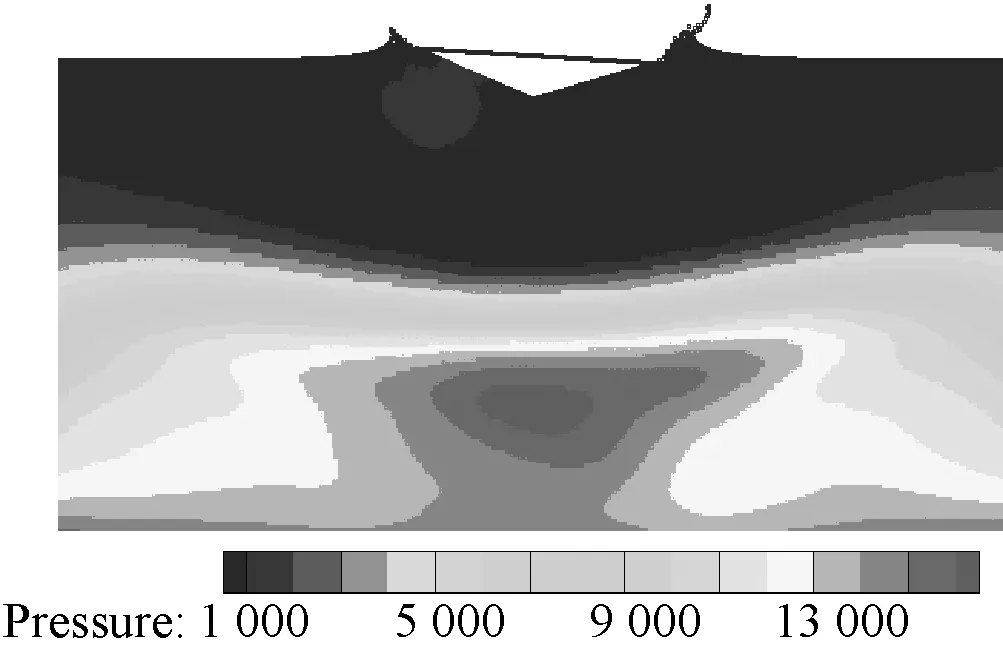
(b) t=0.407 s(左、中和右为均匀模型，非均匀变h，非均匀恒定h)

表2则给出了粒子均匀分布模型和粒子扩散分布模型计算效率的比较。和气泡上浮算例类似，这里采用单核测试，计算时间不包括粒子搜索时间。结果表明计算时间节约1/4左右，大幅提高了计算效率。

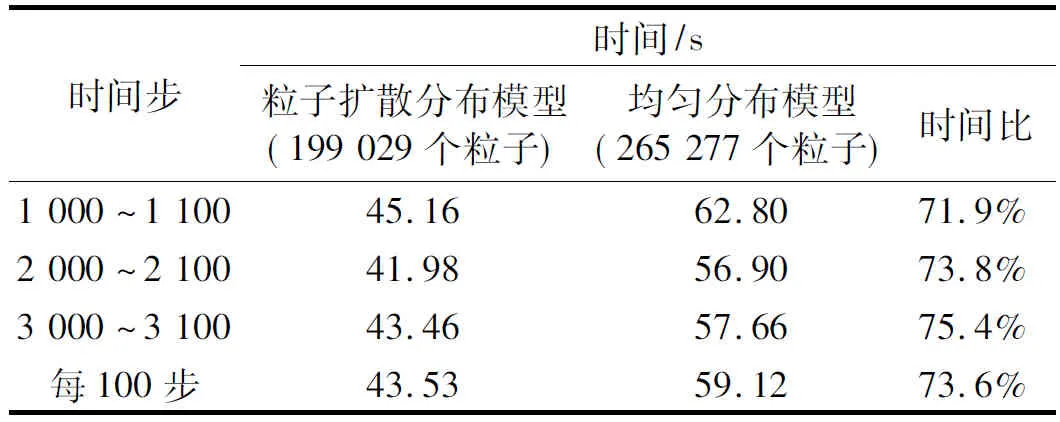
表2 不同粒子分布模型计算时间比较(不包含搜索时间)

3 结 论

为提高计算效率，类似于有限差分法中的网格分布方法，根据计算域中物理量的变化剧烈程度匹配相应疏密的粒子分布，构建了粒子扩散分布模型。然后给每个粒子单独配置相对应的光滑长度，通过对粒子对的光滑长度取算术平均值来实现粒子作用对称化，并对链表搜索法添加了变光滑长度处理。通过气泡上浮和楔形体入水冲击两个典型算例验证了粒子扩散分布模型及空间变光滑长度算法的有效性，结论表明：

(1) 采用粒子扩散分布模型能够有效减少粒子数量，但会引起强不稳定性，导致结果出错。而空间变光滑长度算法可以很好地抑制上述由于粒子分布不均匀导致的强不稳定性，在重点关心的气泡信息和楔形体冲击要素等方面都取得很好的模拟效果。

(2) 合理粒子分布方式下，利用空间变光滑长度算法可以在保证结果准确性的同时大大降低计算成本，为三维复杂工程问题的求解打下基础。但在粒子分布方式的优化、标准化及抑制变光滑长度引起的不稳定性方面需要进一步深入研究。