翻转课堂在高中数学教学中的应用探讨
江苏省苏州市吴江区吴江盛泽中学 孟 俊
对于绝大多数学生而言,教师的教学方法和教学能力是影响学生高中数学学习效果的主要因素。将翻转课堂的教学方法应用到高中数学教学过程中,能够有效提高学生的学习能力,提升学生的学习成绩。
一、集合多种技术手段,突破传统的教学模式
高中数学中的立体几何知识一直是学生的学习重点,也一直是学生学习的难点。在解决立体几何问题时,通常的解题方法就是把图画出来,将有关数据代入,最终解出答案。但是,绘图的过程是困难的,很多学生的绘图技术存在问题,画出来的立体图形不能反映题目中要求的特点,因而就不能够帮助学生有效解决数学问题。在解决这个问题时,利用翻转课堂法是十分有效的。教学人员可以鼓励学生使用一些新的技术手段,让学生了解各类立体图形的几何特点和几何性质。学生对各类立体图形的几何性质和几何特点了解充分以后,在之后的做题过程中将更加得心应手。
例如:设长方体的长、 宽、高分别为 2a、a、a,其顶点都在一个球面上,则该球的表面积为 ( )
A.3πa2B.6πa2C.9πa2D.24πa2
这个题目主要考察的知识点是球内接立方体的几何性质。在解决这个问题之前,教学人员可以通过制作幻灯片的形式来帮助学生归纳球内接立方体的几何性质。利用多媒体手段,学生可以对这种组合图形有更加直观的认识,也能直接找到组合图形的几何性质。根据球的性质,球直径的平方为6倍的a2。学生可以计算出球的表面积为4*π*R2。将得出的半径代入,求出球的表面积为 6*π*a*a,所以选择第二项。
二、结合实践教学内容,提升学生学习积极性
在以往的高中数学教学中,理论教学是主要部分,实践教学仅仅是教学内容中的补充部分。随着高中新课程教学改革的推进,培养学生的实践能力成为高中数学教学重点。数学本身就是来源于社会实践,与社会实践有着十分紧密的联系。传统的高中数学教学内容与生活实践之间的联系较少,对学生实践能力培养的效果是有限的。而翻转课堂的应用内容中就包括理论结合实践,提升学生的学习积极性。当高中数学的教学内容与生活实践的结合更加紧密时,学生的学习兴趣会得到培养,学生的学习积极性也会得到提升。高中数学教学人员增加的实践教学内容要与学生的生活实践相联系,保证学生有一定的能力来完成实践教学中的内容。
例如:某几何体的三视图如图所示,则它的体积是( )
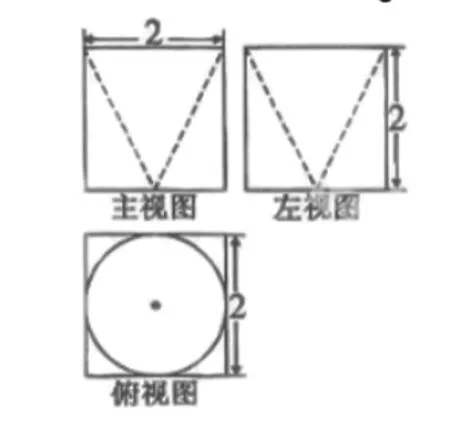
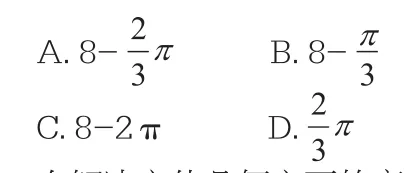
在解决立体几何方面的高中数学题时,很多学生不能直接通过三视图看出立体图形的形状,因此,在解决求体积的问题时经常会遇到困难。但是学生如果利用手中的道具来制作出题目给出的数学模型,就能够快速找到立体图形的性质,找出答案。在这道题中,学生可以明确几何体是由立方体中挖去一个圆锥形成的。计算几何体的体积需要计算立方体的体积和圆锥的体积,由圆可知立方体的体积为8,而圆锥的体积为,那么几何体的体积为8-,选项为第一个。
三、增加小组讨论活动,培养学生的探索能力
增加小组讨论活动,培养学生的探索能力是将翻转课堂应用到高中数学教学中的具体措施。翻转课堂与传统教学方法相比,最突出的特点就是增加了小组讨论的教学活动,小组讨论的教学活动,能够帮助学生在交流的过程中更加深入地理解高中数学知识,明确考点和重点。在传统的教学模式之中,学生的学习方式是完全依靠教师和个人,与同学、教师之间的交流很少。在学生遇到一些复杂的数学问题时,常常会因为教师精力有限而得不到及时的解决。但是在高中数学教学中增加小组讨论的活动之后,学生遇到的数学问题可以在课堂上解决,可以通过小组同学直接解决。增加小组讨论的教学活动,还能够培养学生的探索能力。通过与小组同学的共同学习,高中学生可以探索学习一些较为困难的数学知识。学生探索学习的过程,也是学生能力提升的过程。
例如:在空间中,下列命题正确的是( )。
A.平行直线的平行投影重合
B.平行于同一直线的两个平面平行
C.垂直于同一平面的两个平面平行
D.垂直于同一平面的两条直线平行
在解决这些问题时,教学人员可以鼓励学生进行小组讨论,每个小组成员要合力对所有的选项进行分析,找出每个选项中存在的错误,最终确定题目的答案。这个题目主要考查的知识点为空间直线与平面的位置关系及线面垂直与平行的判定和性质定理。第一个选项中,平行直线的平行投影不一定重合。第二个选项中,平行于同一直线的两个平面可能垂直。第三个选项中,垂直于同一平面的两个平面可能垂直。第四个选项正确。
将翻转课堂教学法应用到高中数学教学中,是改善教师教学效果、提升学生学习能力的重要途径。但是,具体的应用模式仍然需要广大教学人员的不断探索。本文笔者主要阐述了翻转课堂在高中数学教学中的应用措施,即集合多种技术手段,突破传统的教学模式;结合实践教学内容,提升学生学习积极性;增加小组讨论活动,培养学生的探索能力。

