从教材内容的疑点处挖掘核心素养的生长点*—以“椭圆的定义”为例

广东省东莞市教育局教研室(523125) 易文辉

1、问题的提出

新修订的课程标准要求高中数学教学以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质[1].核心素养为纲的理念如何转化为广大教师教育教学的实际行动,是目前教学中研究的重点和热点.教材是师生教与学的主要素材,决定了课堂教学的内容,是从“四基”“四能”通向核心素养的主渠道[2].多年来大家已经形成的共识是要“用教材”而不是“教教材”,理解好教材内容,把握内容本质,决定了学生数学学科核心素养的达成度.

专家们在编写教材时,注重整体知识结构的综合性、全面性,使教材的科学性、思想性、时代性、现实感以及亲和力得到保障[3].但在实际教学中,教材只是学术形态的数学转化为教育形态的数学的一个中介,还需要教师进行“智慧”地处理,才能用好教材.目前,教材中的内容编排或者编写要转化为教育形态的数学,仍然存在许多疑点,而这些疑点往往就是核心素养培养的生长点,是用好教材的一个抓手,以人教版选修2-1 A版中“椭圆及其标准方程”一节为例,教师要根据教材中存在的疑点,使之成为教学的有利于学生核心素养培养生长点.

2、教材“椭圆的定义”的疑点分析

疑点1椭圆的画法是怎么产生的?

根据课程标准的要求,平面解析几何的单元学习中,要帮助学生认识椭圆的几何特征,教材通过探究,也就是一种画椭圆的方法,通过画图揭示椭圆上的点满足的条件,从而得到椭圆的定义.教材的这种引入方式,想法是很好的,但是教师非常难处理,不知道这种画法是怎么产生的,学生就更加不清楚了,不少老师处理方式是类比画圆的方法,从一个定点(圆心),变为两个定点,过渡到教材中的实验.然而,经过调查和多年来教学实践发现,学生对此是非常疑惑的,为什么定点是2个,而不是3个?为什么是距离之和,而不是距离之差呢?显然这些疑惑是不能忽视的,因为这些疑惑正是对椭圆知识发生过程的疑惑.

教材这种处理,突然冒出来个“椭圆”,是会“伤害”学生对数学的兴趣的,为什么要学习椭圆知识?椭圆从哪里来的?没有将椭圆的概念建立在学生已有的生活经验或者已有的知识中,未能感受到学习它的必要性,也没有经历椭圆的形成过程,怎么能不让学生感觉到数学的冷呢.

疑点2画椭圆过程中那两个定点是随便选的吗?为什么只关注长度关系?

在画椭圆的探究过程中,将细绳两个端点抽象成两个定点F1,F2,笔尖是平面内一个动点M,笔尖拉开的两段细绳,是动点M在运动变化时到两个定点F1,F2的距离,然后让学生观察到这两个距离之和等于一个常数,不少的老师还通过几何画板验证,让学生观察发现结论.然而,实际上这种目的性非常强的探究是意义不大的,学生难免会产生疑问,为什么要观察这两条线段之和?不能是差?或者是积或者商?更甚至,几何中常常通过距离和角度来刻画相对位置关系,那么将这个实验抽象为平面内点、线关系之后,动点M在运动变化过程中,不但线段长度发生了变化,还有角度也发生了变化,为什么不研究角度之间的关系呢?要发展学生的核心素养,一定不能只关注结果性知识,更应该关注过程性知识,只有将知识的产生和发展过程嵌入教学之中,而且教学过程也要渗透不确定性知识,例如画椭圆这个实验中,除了距离之和等于一个常数是确定性知识,还有这个距离之差、积、商都是不确定的,角度的关系也存在不确定性关系,从培养学生理性思维,学会用数学的眼光观察世界的素养来看,这些不确定性关系在寻找到确定性关系的过程中同样重要.

疑点3确定一个椭圆之后,两个焦点能找出来吗?

在画椭圆的试验中,先定好了两个定点,然后拉直绳子才能画出椭圆,这两个定点就是椭圆的焦点,意味着只有椭圆的焦点定了才能有椭圆,学生难免会疑惑,是否所有椭圆都能有焦点呢?如果有,是否可以有办法找出两个焦点?这两个定点究竟在平面内是什么位置?要培养学生严谨求实的精神,就不能用“以后你就知道了”去搪塞学生,而是要尽可能理清知识的来龙去脉,帮助学生理解知识的本质.

3、改进教学设计,挖掘数学核心素养的生长点

要解释这么多疑点,显然不是单纯的简答题,根本在于教学观、教材观的问题.数学核心素养生成的本源是知识[4],也就是说数学核心素养就在知识的来龙去脉、知识的发生发展过程中生成,而“椭圆及其标准方程”一节中,教材上的处理突兀、生硬,需要教师进行“再加工”,搞明白椭圆是怎么来的?为什么要研究椭圆?是怎么研究椭圆问题的?等.

历史上,古希腊人先是从圆柱或圆锥被平面截得的截口上发现椭圆;公元前3世纪,阿波罗尼奥斯在《圆锥曲线论》中采用了截线定义,并导出了“椭圆的焦半径之和等于常数”这一性质;公元6世纪,拜占庭数学家安替缪斯利用该性质给出的“两钉一线”画法;17世纪,法国数学家拉伊尔将椭圆定义,为平面上到两定点距离之和等于常数的动点轨迹;直到1822年,比利时数学家旦德林利用圆锥的两个内切球,导出椭圆焦半径性质,从而使截线定义和轨迹定义统一起来[5].纵观数学史,椭圆的发展有以下重要环节椭圆的发现、截线定义的形成、基本性质的推导、焦半径性质的获得、机械作图的产生、轨迹定义的确立、椭圆方程的推导.教材上只呈现了后面三个环节,虽然简练,但是将椭圆最核心的发生发展过程给割裂了,不利于学生学习,更不利于学生核心素养的生成.

由于内容容量大,建议教学中“椭圆及其标准方程”分成两个课时,第一节课主要是椭圆的定义,第二节课推导椭圆的标准方程.根据以上分析,建议改进教学设计,改变教学内容的呈现方式,可以通过生活中的椭圆入手,重构历史,让学生经历从截线定义到轨迹定义的知识发生过程,帮助学生厘清椭圆的来龙去脉,椭圆定义教学过程主要环节的设计:

学生活动:观察生活中与椭圆有关的情境.

图1

图2

图3

图4

问题1对于第四张图中,当平行光照射篮球时,影子轮廓的形状有什么变化?轮廓上的点到篮球与地面切点的距离有什么变化?

设计意图由学生熟悉的情境引发思考,当光线在篮球正上方发时,影子轮廓是一个圆,此时圆心是球与地面的切点,影子轮廓上的点到切点的距离等于一个常数;当光线斜照时,影子轮廓是形成的是椭圆,显然影子轮廓上的点到切点的距离会随点的位置变化而变化.

问题2将平行的光线看成是与球面相切的圆柱面,椭圆与圆柱面有什么关系?

设计意图由光线斜照篮球在地面形成的轮廓,将篮球抽象成球,与球面相切平行光线抽象成为圆柱面,地面抽象成为一个与球相切的平面,这时椭圆就是圆柱面与平面的交线,如图5所示.

图5

问题3如图6,假设球与平面相切于F,椭圆上一点P,过点P的母线与球相切于Q,则P点移动的时候,PF与PQ的变化有什么关系?

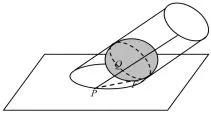
图6

问题4根据对称性,图6中的椭圆还可以怎么得到?你能发现椭圆上点P在运动的过程中,有什么样的不变的长度关系?

设计意图根据对称性,让学生经历由图7到图8的变化,将圆柱在平面下方部分补完整,也可以看成另一边也有一个同样大小的球,与平面相切,设切点为E,过点E的母线与球交于点M,则有PE=PM,PF=PQ,而PM+PQ=MQ(定长),从而得到PE+PF=定长,学生能够体会到“椭圆上的点到两个定点间的距离是一个常数”,是自然的,而不是“变戏法”一样突然冒出两个定点.

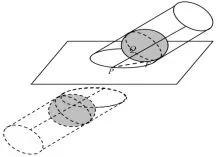
图7

图8

问题5用一个不平行于底面的平面截圆柱得到的图形是什么?在该截面内是否依然存在两个定点,使得所得图形上任意一个点到这两个定点的距离都是一个常数?

设计意图从一般的角度思考椭圆的特征.学生容易直观得到用不平行于底面的平面截圆柱所得的图形就是一个椭圆(截线定义),通过截面上下补回两个大小一样球,使得球与截面都相切,切点就是索要找的两个定点,至此,将球和圆柱去掉,抽象出椭圆上点的本质特征,椭圆的定义形成就水到渠成了,师生共同总结、提炼:我们把平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫椭圆的焦点,两焦点间的距离叫做椭圆的焦距.

关于焦点的名称可以简单向学生介绍,椭圆有非常重要的光学性质应用到实践中,例如放电影的灯泡的反射镜面就是椭圆面,由椭圆的两个定点F1,F2,任意个定点发出的光线,都活聚焦到另一个定点,因此我们把这两个定点F1,F2,称为椭圆的焦点这样既能激发学生兴趣,又能直观感受到数学是“自然”、“讲道理”的.

以上环节通过生活中的椭圆,抽象成数学中的椭圆,从基于对应的抽象,根据球的切线性质,过渡到基于内涵的抽象,培养学生数学抽象、逻辑推理、直观想象的核心素养,体会用数学的眼光观察生活中光照篮球的现象,用数学的思维思考球、截面、圆柱之间的关系,用数学的语言描述椭圆的特征,这本身就是完整的一个抽象、推理、模型的过程,就是核心素养培养的过程.

4、结束语

培养学生核心素养的就是要“教好数学”,前提就是教师要理解好数学,理解数学内容从何而来,本质是什么,以及将来的发展方向,在教材编写过程中,专家们既要考虑教材的科学性、可读性,还要考虑教材的逻辑结构体系,对数学的理解也未必就符合学生的心理规律,教材也不能方方面面兼顾,难免会有交待不清楚或者没法交待清楚的情况,比如椭圆及其标准方程中,除了椭圆的定义之外,后面内容中,比如为什么要设|MF1|+|MF2|=2a?为什么椭圆方程√还要化简?为什么要选择通过移项两边平方的方式化简方程?为什么叫标准方程?标准的含义是什么等,这些都是需要教师去搞清楚的,然后才能让学生明白,从而更加理解数学本质.

作为教师用教材的前提就是要吃透教材,多研究几个“为什么”,真正把数学知识的来龙去脉搞清楚,在教材的“疑点”处多去挖掘,教知识的同时,有机融入数学文化,让学生体会数学的来龙去脉;注重知识的发生、发展过程,体验数学从抽象研究对象,到建构数学模型的全过程;注重数学内容教学的同时,又要能够和学生的生活、实践联系起来,学会用数学的眼光观察世界;既要注重证实也要注重证伪的教学,让学生体会“直觉思维”在形成确定性结论过程中的重要性,才能在教学中真正培养学生的核心素养.