异步热轧高锰无磁钢剪切应变场有限元分析

赵 峻 周 玉 王晓玉 童宣宝

（巢湖学院 机械工程学院，安徽 巢湖 238000）

无磁钢是一种在磁场中磁化作用非常微弱，基本不产生磁感应的低磁性钢铁材料，被广泛应用于家用电器、交通运输、航空航天等重要领域。随着社会的发展，各行业对无磁钢的性能提出了更高的要求，迫切需要制定新工艺、新技术以提高其性能，扩展其使用范围[1-2]。利用异步轧制上、下表面线速度差，使其在变形区形成的剪切变形可细化晶粒，从而达到提高力学性能的目的[3]。因此，研究坯料内部剪切变形行为的规律对制订合理的轧制工艺规程具有一定的指导意义。

娄依志等[4]模拟了大断面收缩率轴类零件的楔横轧二次楔轧制成形过程，分析了轧制过程中断面的应力应变场分布规律；张文东等[5]对H型钢进行多道次轧制有限元模拟，分析了稳定轧制过程中应变的特点。在腹板部位的应变最小，翼缘部位较高，腰腿连接部位的应变最大。袁思波等[6]利用Simufact有限元分析软件分析了合金管材在轧制压延过程中应力和应变场分布情况。关于高锰无磁钢异步热轧过程的剪切应力场已有详细报道[7-8]，但对于剪切应变场的系统研究报道较少。本研究基于MSC.Marc有限元模拟软件，采用热力耦合的刚塑性有限元法建立高锰奥氏体无磁钢板带异步热轧过程的有限元分析模型，对高锰无磁钢的异步热轧过程进行研究，分析轧制过程中初轧温度、压下量、异速比对剪切应变场的影响规律，为制定合理的轧制工艺提供理论依据。

1 有限元模型的建立及参数的选择

1.1 有限元模拟参数的选择

采用二维两辊轧制有限元模型模拟高锰无磁钢的异步热轧过程。本有限元模型上、下工作辊直径相同，上辊转速不变，通过调整下工作辊的转速，模拟不同的轧制异速比方案；利用不同的板坯入口厚度模拟不同的压下量方案。模拟所用轧制参数见表1。

表1 异步轧制模拟参数

1.2 有限元模型的建立

1.2.1 几何模型的建立

因轧件头部、尾部是非稳定轧制区域，为了数据结果的准确性，以轧件中间区域作为分析对象。有限元分析的精度与网格尺寸大小有着密切的关系，网格尺寸越小，模拟结果精度越高。已有文献研究表明，当有限元模型网格尺寸小于0.285 mm时，模拟结果真实可靠[8]。刚塑性有限元求解时，对板带材一类简单断面轧制问题时，采用数百单元足以得到满意的求解精度。本研究采用二维模型，可以增加单元数量，提高结果精度，而不会使计算时间大量延长。有限元模型轧件出口厚度为2 mm，划分10个单元（单元长度0.2 mm<0.285 mm），长度方向划分200个单元，共2000个单元。取轧件中间厚度方向上的11个节点作为研究对象。异步轧制有限元模型如图1所示。在图1所示几何坐标系中，X轴正方向为轧制方向，Y轴方向为工作辊压下方向。

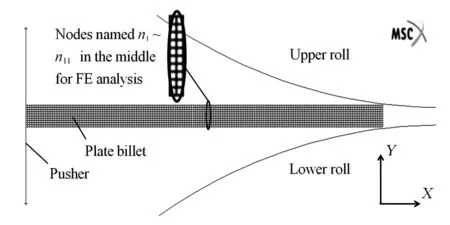
图1 异步轧制过程有限元模型

1.2.2 材料模型的建立

刚塑性有限元法忽略材料的弹性变形，简化分析过程，它融合材料变形过程中的金属流动、加工硬化等各个变形阶段的理论，形成了具有完善理论的模拟和分析方法[9]。有限元模拟的关键环节之一是材料属性的定义，建立准确的材料模型是正确进行有限元模拟分析的基础。在轧制过程中，轧件变形较大，轧辊发生可以忽略的弹性变形。在有限元模型中将轧件定义为变形体，轧辊定义为只产生热交换的刚性体，所以只需建立轧件的材料模型，不需考虑轧辊的属性。为了得到准确的模拟结果，所有的材料属性都考虑了温度的变化。轧件的热传导系数h、线性膨胀系数λ和比热容系数c随温度变化参数见表2。

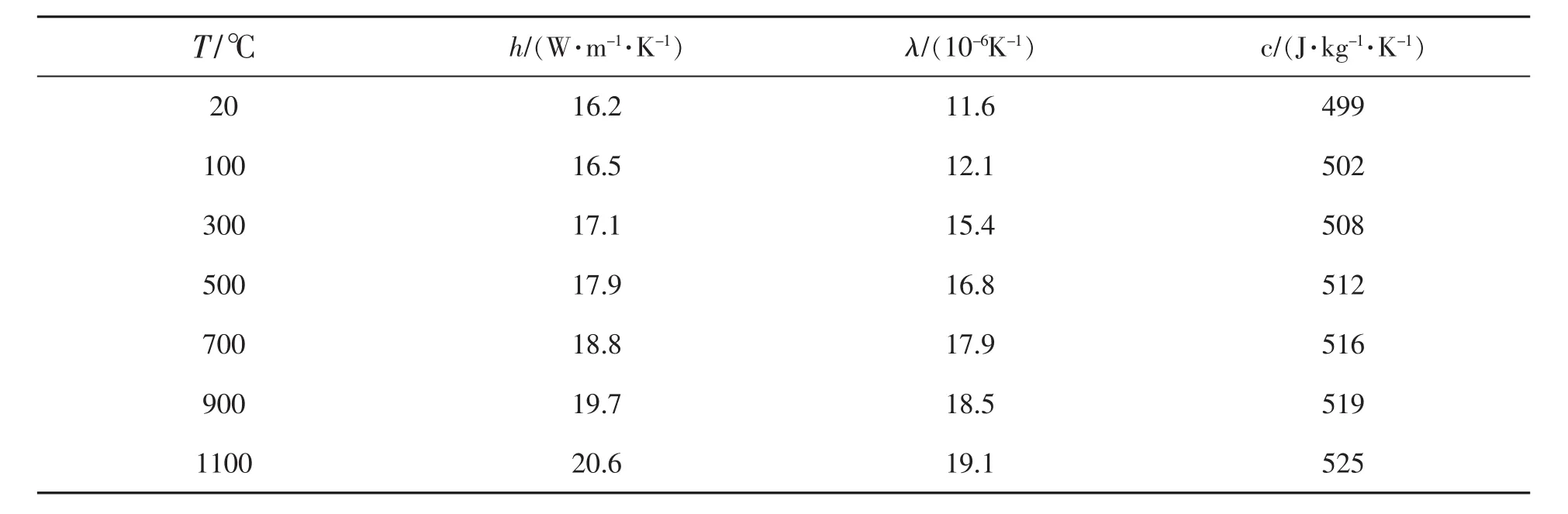
表2 轧件热物理参数

变形抗力模型是轧制过程中基本的数学模型之一，它的精确程度将直接影响到模拟结果的准确性。本模型中采用的变形抗力数学模型如式1所示：

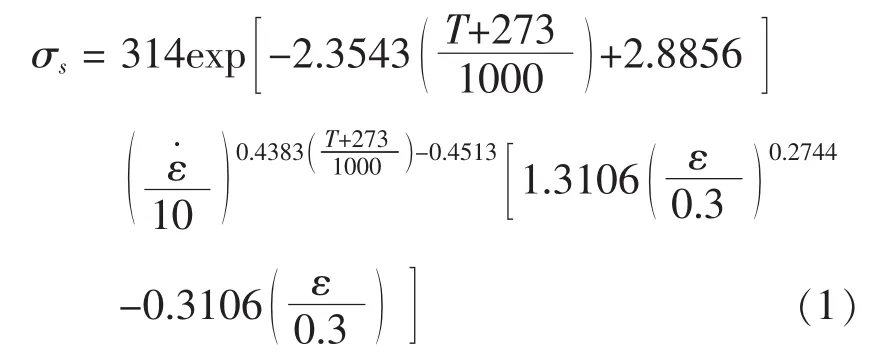
式中，σs为变形抗力，单位为Mpa；T为变形温度，单位为℃；ε 为真实应变；ε˙为应变速率，单位为 s-1。

2 有限元模拟结果分析

2.1 异速比对剪切应变场的影响

有限元模拟高锰奥氏体无磁钢在初轧温度为1050℃，坯料入口厚度为2.50 mm，异速比为1.00和1.15时轧制变形区剪切应变场的有限元模拟结果如图2所示。从图2可以看出：当异速比为1.00时，剪切应变的绝对值沿板坯心部向上下表面逐渐增加，并呈对称分布，上、下表面剪切变形最大，心部剪切应变为零，不发生剪切变形。当异速比大于1.00时，剪切应变绝对值从下表面的入口侧到上表面的出口侧呈逐渐增大的趋势（C→D→E），这样在变形区内沿板坯厚度方向就存在一个剪切变形带。

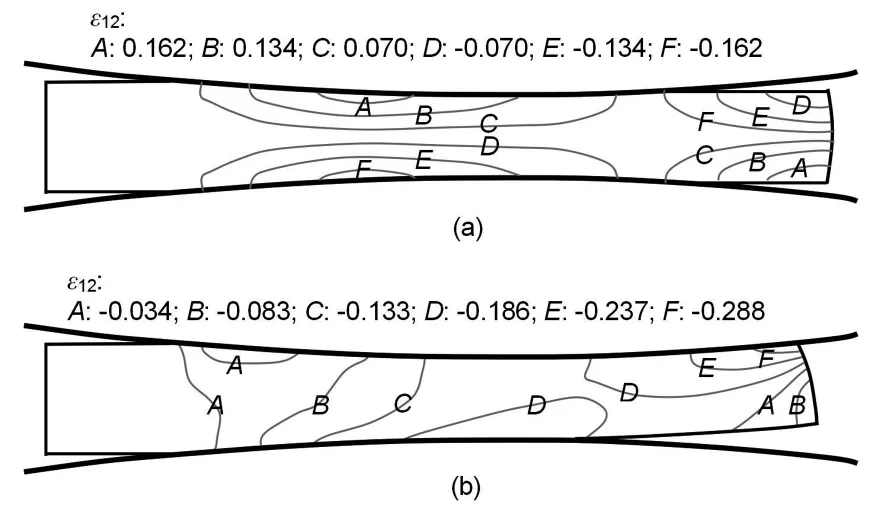
图2 异速比为 1.00（a）和 1.15（b）下的剪切应变场（h0=2.50 mm、Ti=1050℃）

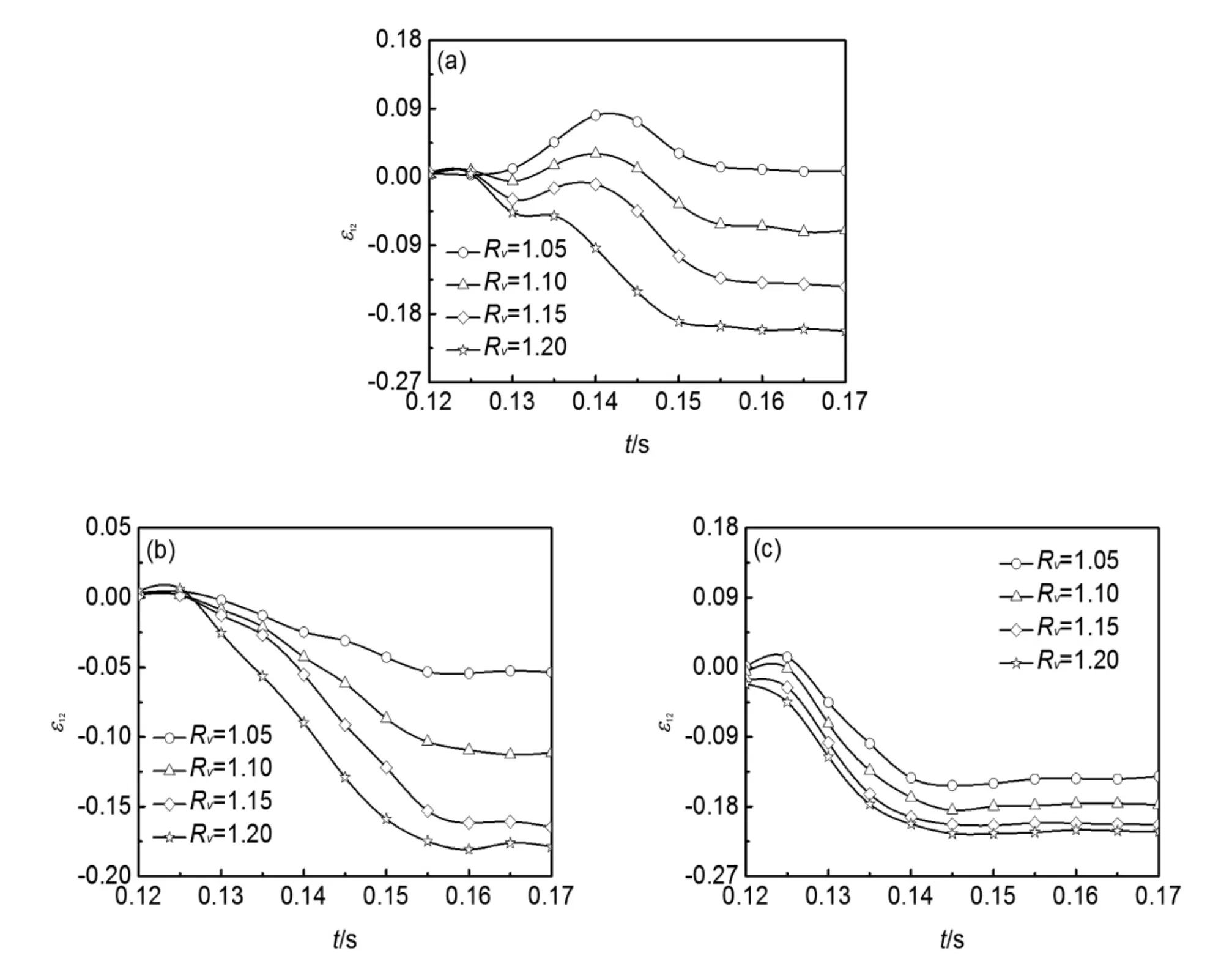
图3 不同异速比时上表面节点（a）、中间层节点（b）和下表面节点（c）的剪切应变变化曲线（Ti=1050℃、η=20%）

压下量η为20%、初轧温度为1050℃时，高锰无磁钢板坯中间垂直断面上表面节点n1、中间层节点n6、下表面节点n11在不同异速比下的剪切应变随时间变化的曲线如图3所示。从图3可以看出：随着异速比的增加，上表面节点从正剪切应变逐渐变为负剪切应变，且逐渐减小，其剪切应变的峰值绝对值逐渐增大；中间层和下表面节点具有相同的变化规律，剪切应变都为负值，其峰值绝对值都随着异速比的增加而增大，增幅随着异速比的增加而减小。由此可见，不同异速比条件下，下表面的剪切应变峰值绝对值最大，上表面剪切应变峰值绝对值最小。异速比的变化对上、下表面节点和中间层节点的剪切应变具有较大的影响。

2.2 初轧温度对剪切应变场的影响

高锰奥氏体无磁钢板坯在异速比为1.10、入口厚度为2.5 mm、初轧温度为950℃和1100℃时，轧制变形区剪切应变场的有限元模拟结果如图4所示。从图4可以看出，在不同的初轧温度下，变形区内的剪切应变分布具有一定的相似性，可见初轧温度的值对剪切应变的分布影响较小，对比图 4（a）和（b）可以看出，剪切应变绝对值随着初轧温度的增加而增大。

压下量为20%、异速比为1.10时，高锰奥氏体无磁钢板坯中间垂直断面上表面节点n1、中间层节点n6、下表面节点n11在不同初轧温度下的剪切应变随时间变化的曲线如图5所示。从图5可以看出：随着初轧温度的增加，上、下表面节点的剪切应变绝对值峰值减小，中间节点的剪切应变绝对值峰值增大；相同时刻，下表面节点的剪切应变绝对值最大，上表面节点的剪切应变最小。对比图5（a～c），可见初轧温度的变化对剪切应变影响较小。

2.3 压下量对剪切应变场的影响

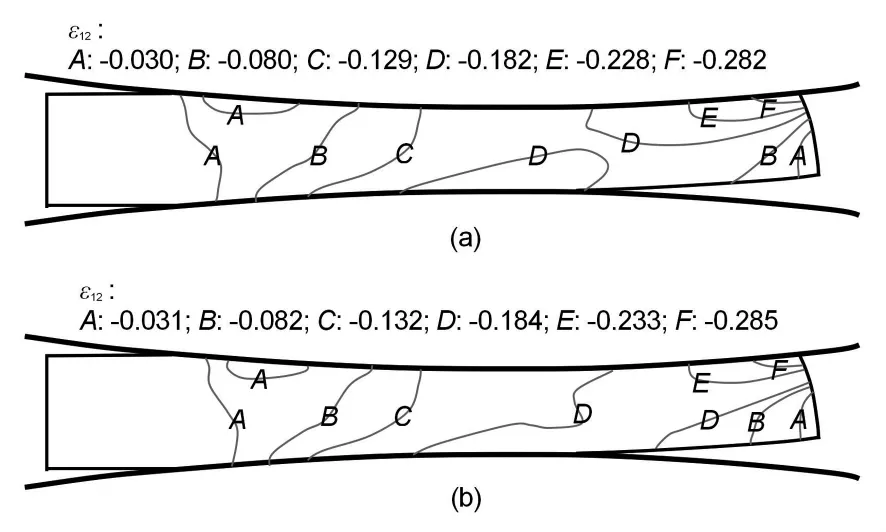
图4 初轧温度 950℃（a）和 1100℃（b）下的剪切应变场（h0=2.50 mm、Rv=1.10）

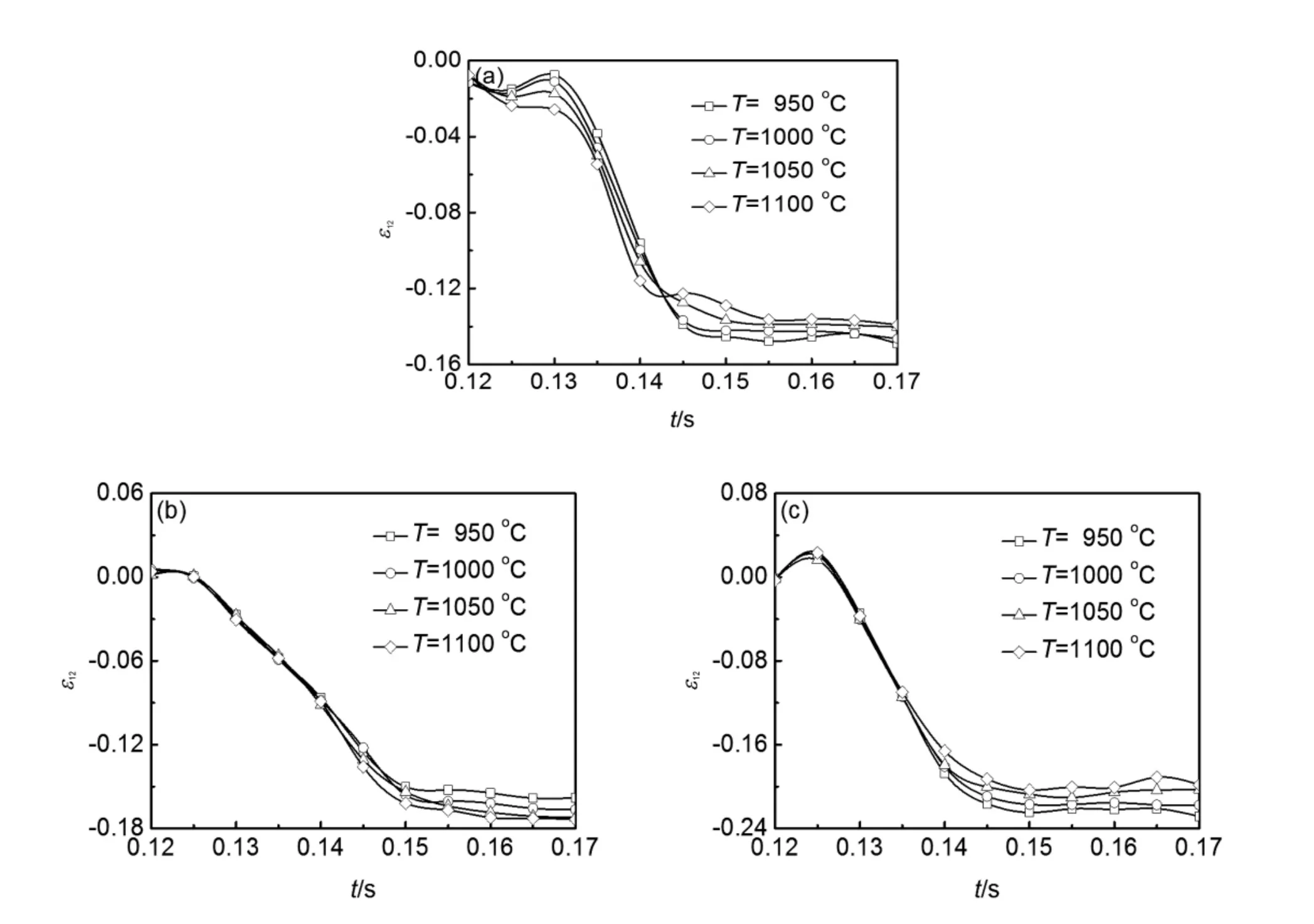
图5 不同初轧温度时上表面节点（a）、中间层节点（b）和下表面节点（c）的剪切应变变化曲线（η=20%、Rv=1.10）

高锰奥氏体无磁钢板坯在初轧温度为1050℃、异速比为1.10、入口厚度为2.22 mm和2.85 mm时，轧制变形区剪切应变场的有限元模拟结果如图6（a～b）所示。从图中可以看出，随着压下率的增加，相同区域的剪切应变绝对值增加，增幅较为明显，并且剪切变形带的区域逐渐增大的趋势。可见，压下率的变化对剪切应变的分布具有较大的影响。

初轧温度为1050℃、异速比为1.10时，高锰奥氏体无磁钢板坯中间垂直断面上表面节点n1、中间层节点n6、下表面节点n11在不同压下量下的剪切应变随时间变化的曲线如图7所示。从图7中可以看出，当压下量大于20%时，上表面节点剪切应变曲线存在一个正值的波峰，且随压下量的增加而增大。上表面的剪切应变绝对值随着压下量的增大先减小后增大。中间层和下表面节点剪切应变都表现为负值，其绝对值随着压下量的增大而增大，下表面节点的剪切应变绝对值最大。

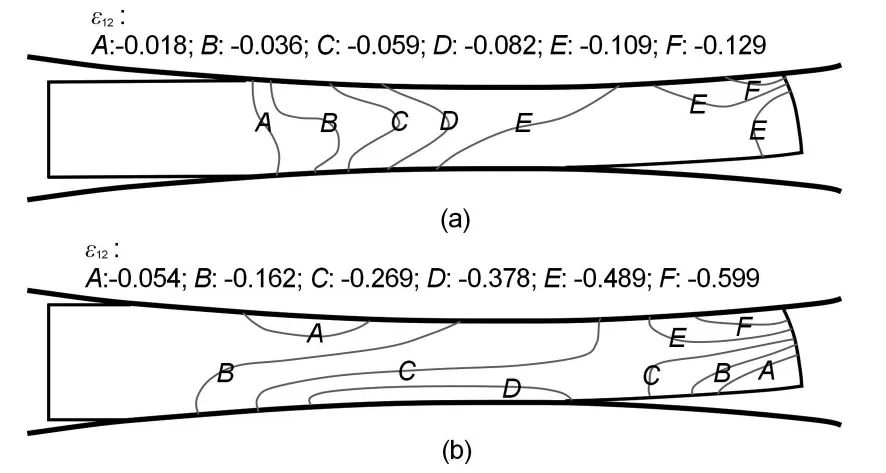
图6 坯料入口厚度为2.22 mm（a）和2.85 mm（b）下的剪切应变场（Ti=1050℃、Rv=1.10）

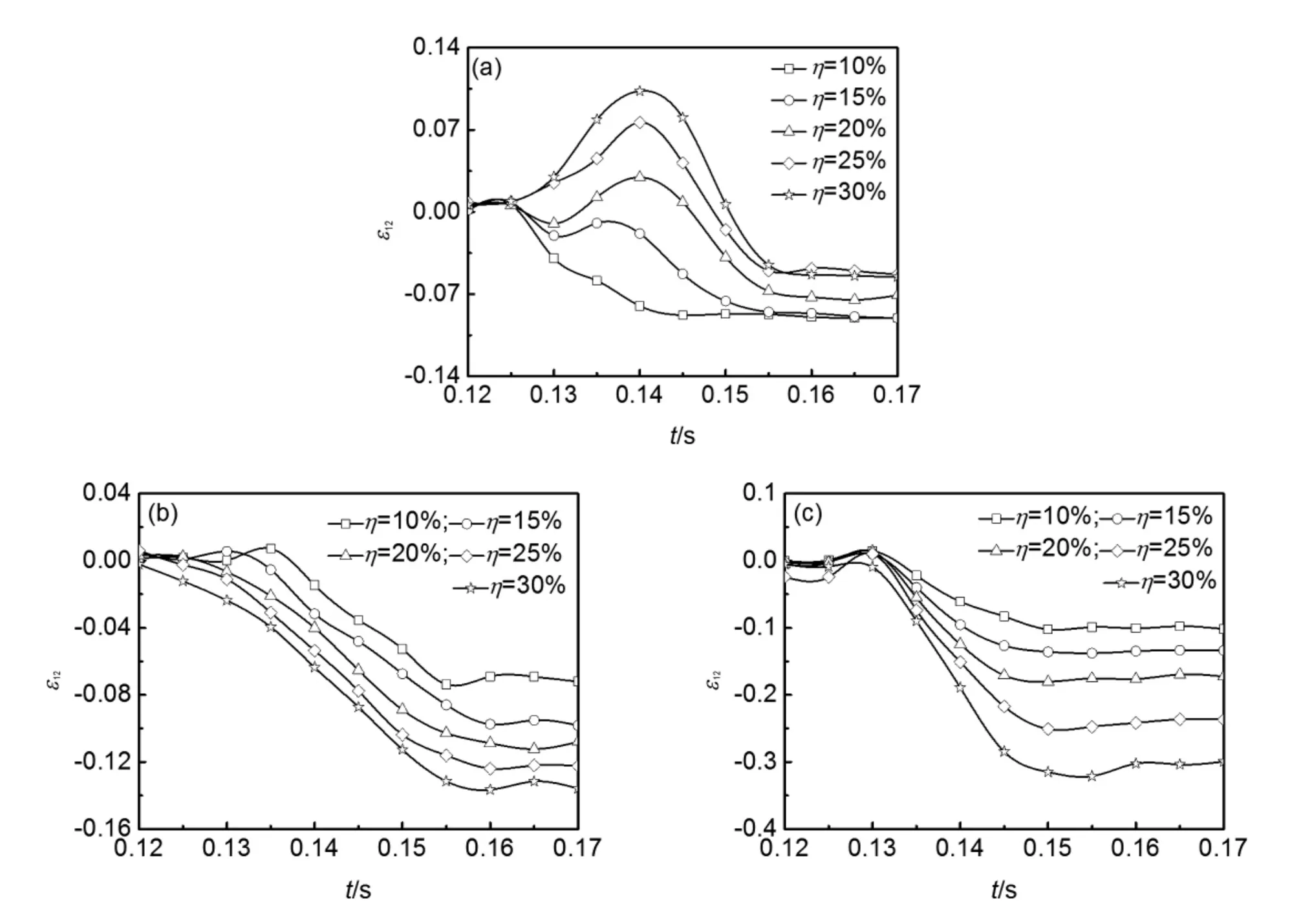
图7 不同压下量时上表面节点（a）、中间层节点（b）和下表面节点（c）的剪切应变变化曲线（Ti=1050℃、Rv=1.10）

3 结论

（1）当异速比为 1.00（同步轧制）时，板坯心部剪切应变为0，并由心部向表面逐渐增加，相对于水平中心线呈对称分布。当异速比大于1.00时，从下表面的入口侧到上表面的出口侧剪切应变绝对值呈逐渐增大的趋势，从而形成剪切变形带。

（2）随着异速比和压下量的增加，中间层节点和下表面节点最大剪切应变的绝对值呈逐渐增大的趋势，上表面节点的最大剪切应变绝对值先减下后增加。

（3）随着初轧温度的增加，上、下表面节点最大剪切应变的绝对值呈逐渐减小的趋势，中间层节点最大剪切应变的绝对值逐渐增大，但增幅不明显。