磁浮平面电机Halbach磁钢阵列中梯形磁钢的应用*

刘广斗，张红梅，明五一

（1.中国石油大学（华东）机电工程学院，山东青岛 266580；2.广东华中科技大学工业技术研究院广东省制造装备数字化重点实验室，广东东莞 523808）

0 引言

在许多工业设备中，例如拾取和放置装置、光刻机以及检测系统等，都在平面上定位和运动。磁浮平面电机因为结构简单，高速以其高精度受到越来越多的关注[1-4]。在磁浮平面电机中使用的是Halbach磁钢阵列[5-6]，如图1所示。此阵列由于磁钢排布的关系具有单边性，能够使一侧的磁场增强，且强磁场具有良好的正弦分布，可以降低电磁力的波动。同时，磁浮平面电机中无铁芯和背铁，降低电机总体质量，这在高加速装置中是很好的优点。

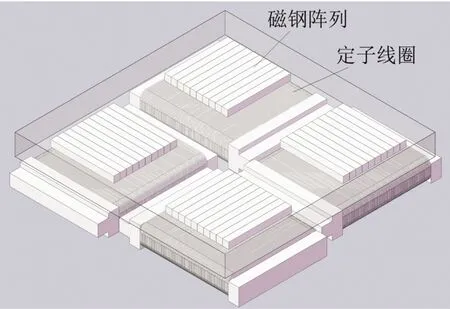
图1 磁浮平面电机结构示意图Fig.1 The structure diagram of magnetically levitated planar motor

Halbach阵列是由Klaus Halbach首先提出，现在已经广泛应用在直线、管状、平面等各种磁浮电机中。经过长时间的应用和发展，不仅仅是矩形磁钢，还有一些三角形、梯形等磁钢也开始在Halbach阵列中使用。文献[7]的双边非Halbach阵列直线电机中，使用梯形磁钢替换矩形磁钢，并应用叠加原理得到近似磁场。文献[8]的双边直线电机中，用梯形磁钢组成Halbach阵列，磁场由所有单个磁钢的磁场叠加而得到。文献[9]在管状电机中使用梯形阵列，用叠加原理得到并分析磁感应强度，但管状电机阵列与平面电机Halbach阵列的边界条件不同。本文作者推导梯形磁钢组成阵列的磁感应强度解析表达式，通过分析Halbach阵列磁感应强度峰值和高阶谐波误差得到最优的y向磁化磁钢边长与极距比值，并分析梯形磁钢对阵列空隙磁感应强度的影响。

1 梯形磁钢阵列建模

1.1 梯形磁钢阵列

在磁浮平面电机中，用梯形磁钢替换矩形磁钢得到梯形磁钢阵列[10]，如图2所示。梯形磁钢也可以通过改变转角θ由矩形磁钢得到。其中，箭头表示磁场方向是由S极指向N极。τ是磁钢阵列的极距，τm是y向磁化磁钢底边的长度，h是磁钢阵列的高度。

图2 梯形磁钢阵列Fig.2 The trapezoidal magnets array

计算梯形磁钢阵列磁感应强度用到如下假设：

（1）磁钢阵列在x方向无限延伸，因此磁钢阵列的端部效应可以忽略；

（2）磁钢均匀磁化。

根据上述假设，把磁钢阵列划分n等份，如图3所示。应用叠加原理，整个梯形磁钢阵列的磁感应强度可由n层矩形磁钢阵列的磁感应强度相加得到。选取其中一层，即第i层进行分析，计算第i层磁钢阵列的结构参数。

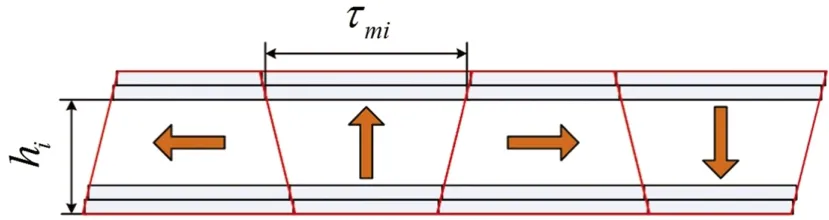
图3 梯形磁钢阵列n层划分Fig.3 The n layers division of trapezoidal magnets array

由图3可知每层磁钢阵列的极距都相同。图4是梯形磁钢阵列的第i层y向磁化梯形磁钢，根据梯形磁钢的尺寸参数，第i层磁钢阵列的参数如下

式中：hi和hi+1分别是第i层磁钢阵列的底边和顶边高度，τmi是第i层y向磁化磁钢底边的长度。

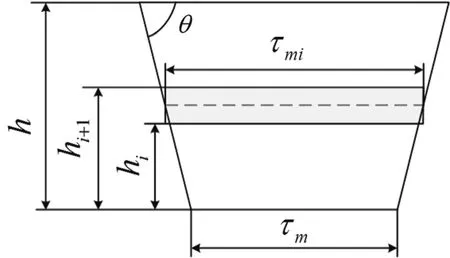
图4 磁钢阵列的第i层y向磁化梯形磁钢Fig.4 The y-direction magnetized trapezoidal magnet in the i layer of magnets array

1.2 第i层磁钢阵列的磁感应强度

磁钢阵列中只有x和y方向磁化的磁钢，所以磁钢阵列为二维磁场分布[11]。第i层磁钢阵列的磁化强度可以表示为：

图5为第i层Halbach磁钢阵列的x和y向磁化强度分布。由前面假设不考虑磁钢阵列的端部效应，使用傅里叶级数得到第i层Halbach磁钢阵列的磁化强度表达式

式中：k是谐波数，Br是磁钢剩余磁化强度，μ0是真空磁导率。

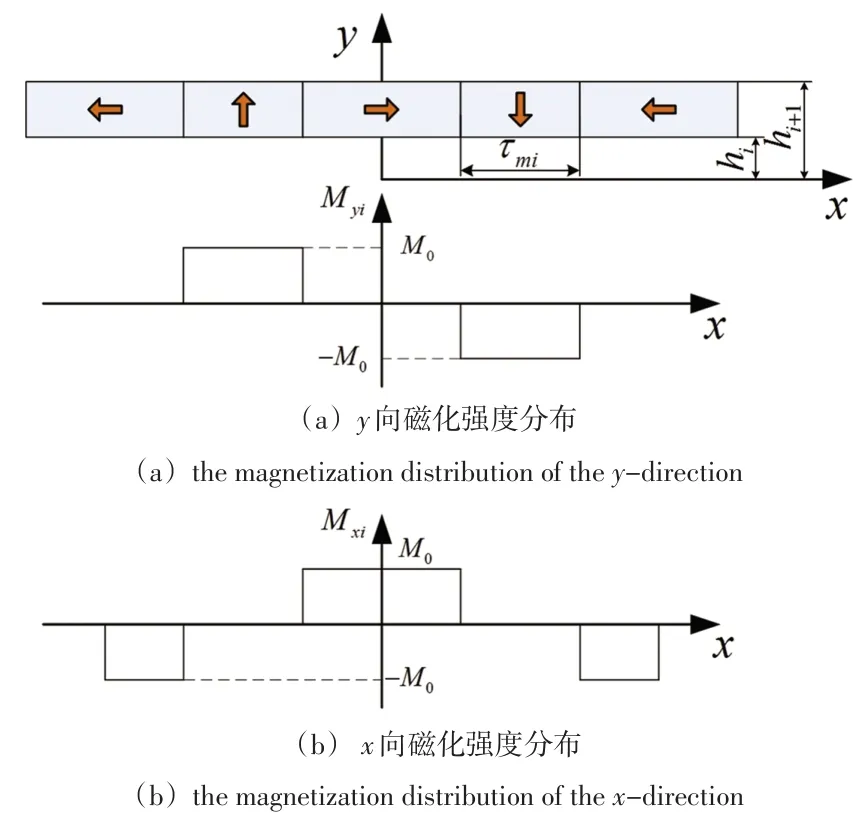
图5 第i层Halbach磁钢阵列Fig.5 The i layer of the Halbach magnets array

计算第i层Halbach磁钢阵列的磁感应强度，可以划分3个区域，如图6所示。区域1和3为空气，区域2为磁钢阵列。因为没有外加电流，所以引入磁标势计算磁钢阵列磁感应强度。由麦克斯韦方程组，各个区域的控制方程如下：

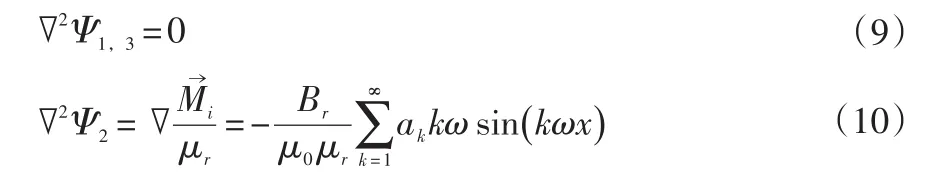
式中：Ψ1，3是区域1和3的磁标势，Ψ2是区域2的磁标势，μr是磁钢相对磁导率。

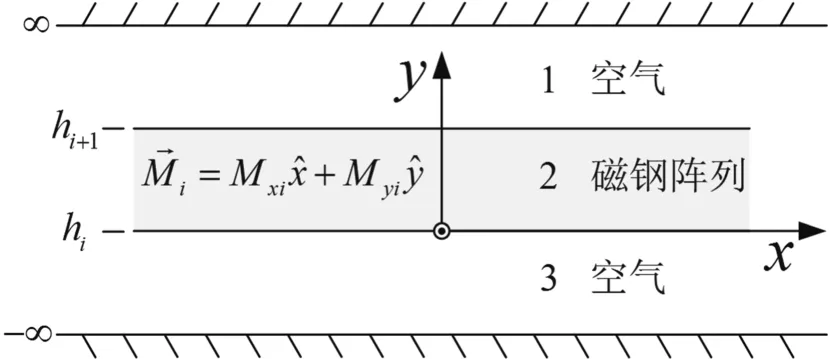
图6 磁感应强度区域划分Fig.6 The division of magnetic flux density

根据磁场中不同磁介质分界面上的边值关系，得到如下边界条件：

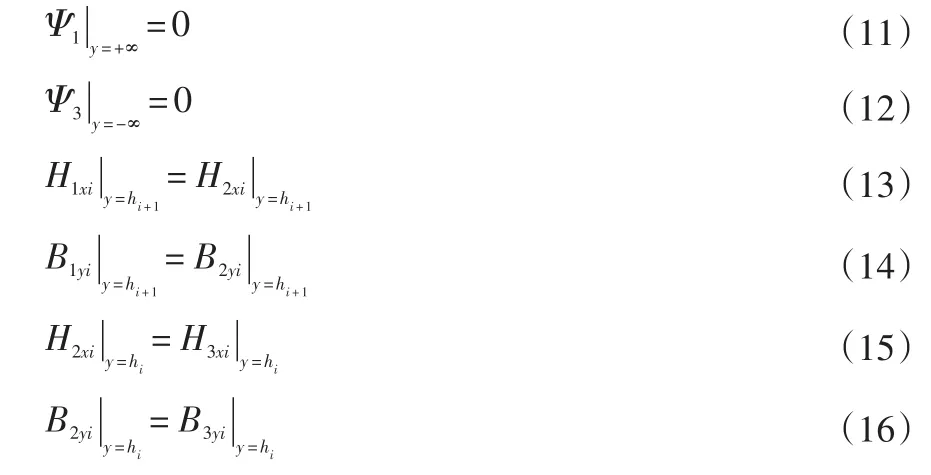
式中：H1xi、H2xi、H3xi分别是区域1、2、3磁场强度的x向分量，B1xi、B2xi、B3xi分别是区域1、2、3磁感应强度的y向分量。

使用分离变量法并结合边界条件求解控制方程（9）和（10）。设定要使用的磁场区域为区域3。在区域3中，磁感应强度与磁标势的关系式如下：

得到区域3磁感应强度的表达式：

1.3 梯形磁钢阵列磁感应强度

根据图6磁感应强度区域的划分可知，每一层Hal⁃bach磁钢阵列的磁感应强度区域分布情况相同，不同之处在于磁钢阵列底边和顶边坐标的变化。所以，由叠加原理得到梯形磁钢阵列的磁感应强度为：

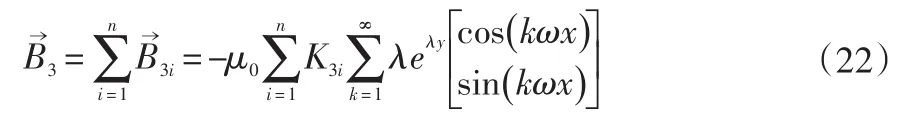
其中，当n趋于无穷大时，得到磁感应强度精确的解析表达式。从工程角度分析，解析模型只需要满足一定精度即可，所以通过对比解析模型和有限元模型来确定n的取值。

设定梯形磁钢阵列的参数为Br=1.2，n=5，τ=20 mm，h=10 mm，τm=5 mm。把解析模型得到的磁感应强度与有限元模型得到的磁感应强度对比，结果如图7所示。观察图形可知，解析模型和有限元模型具有很好的一致性。Bx和By的最大误差分别为0.007 T和0.006 T，占各自峰值的1.77%和1.27%，精度足可以满足工程计算。

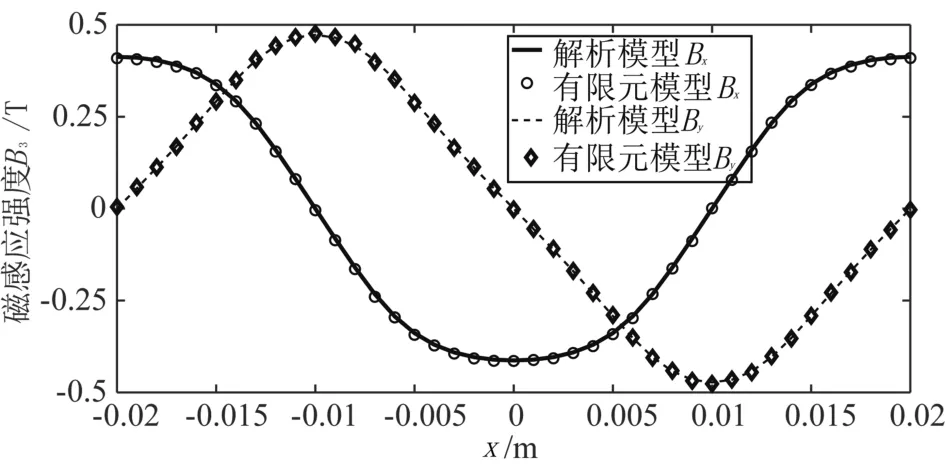
图7 解析模型和有限元模型磁感应强度对比Fig.7 The division of magnetic flux density

2 Halbach阵列参数分析

以Halbach矩形磁钢阵列为例，参数选择一般遵循磁感应强度最大或者高阶谐波最小的原则。通常阵列的极距和高度都为初始设计值，那么y向磁化磁钢的边长τm成为影响磁钢阵列磁感应强度大小的主要结构参数。在磁浮平面电机中，Halbach矩形磁钢阵列的Bx和By分别产生悬浮力和驱动力，其中驱动力大小是平面电机的一个关键指标。因此，对By进行分析选择合适的磁钢阵列结构参数，Halbach矩形磁钢阵列的高度和极距和1.3节的相同。

2.1 谐波磁感应强度

以y向磁化磁钢的边长τm与极距τ的比值为参数，得到By在距离磁钢阵列底边3 mm空隙处各个谐波的峰值，如图8所示。各个谐波的峰值以τm/τ=0.5为中心对称分布，其中3阶谐波有最大的高阶谐波幅值，当τm/τ=0.5，此时基波的峰值最大。

2.2 高阶谐波误差

为了更直观的表示高阶谐波与τm/τ的关系，引入均方根（RMS）表示高阶谐波的误差。均方根的表达式为：

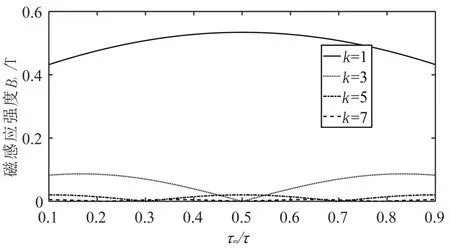
图8 By各个谐波的峰值Fig.8 The peak value of each harmonic in y-component of magnetic flux density

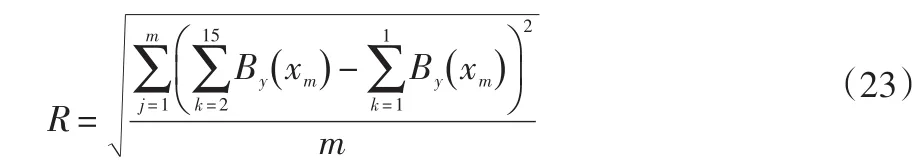
式中：m是x轴所选区域划分的点数。

根据磁感应强度的周期性，选取分析范围x=[0，τ]，划分100等份，距离磁钢阵列底边3 mm。得到高阶谐波的均方根随着比值τm/τ变化的波形，如图9所示。观察波形可知，高阶谐波的均方根以τm/τ=0.5为中心对称分布。当τm/τ=0.5，得到高阶谐波的均方根最小值，即高阶谐波误差最小。

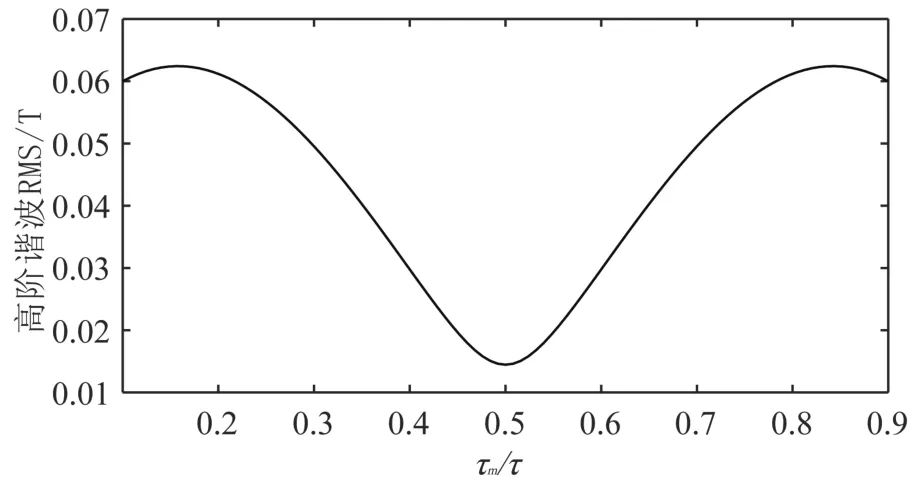
图9 高阶谐波的均方根（RMS）Fig.9 The root mean square of higher harmonics

从上述两个方面分析，τm/τ=0.5既能得到最大的基波峰值，又能得到最小的高阶谐波误差。所以，Halbach矩形磁钢阵列的最优结构参数为τm/τ=0.5。

3 梯形磁钢对磁感应强度的影响

分析改变磁钢形状对空隙磁感应强度的影响，Hal⁃bach磁钢阵列结构参数和1.3节的相同。以转角θ为参数，变化范围与高度和极距有关，在此结构参数下为从45°到135°。得到距离磁钢阵列底边3 mm空隙处By峰值和高阶谐波误差随着转角θ变化的波形，如图10所示。观察图形，可知在50°之后，磁感应强度的峰值随着转角的增大而减小。高阶谐波的误差则是以90°为中心对称分布，而且在90°处高阶谐波误差最小。随着转角的变化，磁钢阵列的磁感应强度峰值变化范围是从0.428 T到0.574 T，变化率达到34.11%。所以，用梯形磁钢可以大范围改变磁钢阵列的磁感应强度，但同时也引起高阶谐波误差的增大。

图10 磁感应强度峰值和高阶谐波误差随转角θ变化的波形Fig.10 The waveform of peak value of magnetic flux density and root mean square of higher harmonics varying with the theta

4 结论

（1）应用梯形磁钢到磁浮平面电机Halbach磁钢阵列，得到梯形磁钢阵列。利用叠加原理，通过磁标势和边界条件得到整个梯形磁钢阵列的磁感应强度解析表达式。并通过有限元模型验证。

（2）分别从磁感应强度最大和高阶谐波最小两方面分析Halbach矩形磁钢阵列，得到最优的结构参数。

（3）分析随转角变化的磁感应强度峰值和高阶谐波误差，梯形磁钢可以大范围改变磁钢阵列的磁感应强度。