GP-平坦模的若干性质

王修建 甘德俊 黄新宇 李福军

（1.皖西学院 金融与数学学院，安徽 六安 237012；2.安徽教育出版社，安徽 合肥 230601）

0 引言

20世纪40年代，纯粹代数研究领域引入了代数拓扑学中的部分概念和方法，它极大地丰富了代数学的研究思路和研究内容，使得同调不变量成为代数学研究的一个重要的核心关键词，并且在这一理论形成的初期，许多代数学家对从代数拓扑中引入的研究对象、研究方法以及研究过程中所思考的问题表现出前所未有的兴趣，投入了大量的研究精力，产出了一大批成果，并逐渐使之发展成为代数学中的一个新的研究方向-同调代数。而同调代数形成和发展也促进着交换代数、代数几何、代数表示论以及李代数等研究领域的发展，尤其是在上世纪50年代，著名的Krull猜想通过同调代数的内容和思路得到了解决，使得国内外数学家日益重视同调代数的研究。近几十年来，同调代数在国内代数界取得了突飞猛进的发展，无论在传统的环论、模论领域，还是在近年迅猛发展的代数表示论领域，同调代数研究及应用都是问题研究的热点。

模论与代数学的许多分支都有着密切的联系，起突出重要作用的是投射模、内射模和平坦模，而投射模、内射模和平坦模是同调代数中最重要的三大模类，可以通过它们有效的研究经典的同调维数，刻画著名的环类，如正则环、QF环、IF环等，以及用来证明环论和代数表示论的许多著名猜想。如Baer于1940年提出的内射性的概念在刻画QF环方面就起着重要的作用，从Baer准则出发，许多学者研究了自内射性的种种真推广。

FP-内射性⇒P-内射性⇒GP-内射性⇒单内射性⇒极小内射性。

然而，平坦模与内射模、投射模有着密切的关系，它也有着各种真推广，一方面Enochs、Jenda等人把投射模、内射模和平坦模拓展到了Gorenstein投射模、Gorenstein内射模和Gorenstein平坦模，促进了相对同调代数的发展；另一方面，国内外代数研究工作者在经典的同调代数中做着不同的真推广，这些研究在特殊环等方面都得到了有益的结果。受这些工作的启发，本研究引入GP-平坦模的概念，并讨论它与GP-内射模的关系及其一些性质，然后尝试用GP-平坦模刻画某类特殊的环，研究GP-平坦维数及其相应的GP-平坦性质。

1 GP-平坦模与GP-内射模

右R-模MR称为平坦模，若对于R的任意左理想I，都有0→M⊗I→M⊗R成立。如上所述，平坦模是模范畴中非常重要的一类模，在环和模范畴的研究中至今都非常重要，近年来一直广受关注，利用平坦模及广义平坦模可以刻画许多重要的环。显然，投射模一定是平坦模，反之不一定成立（注：环R上每个左R平坦模是投射模的充分必要条件是，环R是左完全环。)。众所周知，关于平坦性的问题已经被广泛研究，本研究是在引入GP-平坦模的定义基础上，进一步研究了GP-内射模和GP-平坦模的一点性质，同时也给出了GP-平坦维数的一些性质。文中所考虑的环是指具有单位元的结合环，所考虑的模都是指酉模，各类环与模的定义以及所用各种记号基本上都可在文献[1-8]中找到，后文使用时不再一一说明。

定义1 一个右R-模M称为GP-平坦模，如果对于R的任一元素r，存在m∈N，使得任意的n≥m，n∈N，都有 0→MR⊗Rrn→MR⊗R 成立。

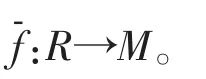
命题1 M是GP-平坦右R模当且仅当 M*是 GP-内射左 R 模，其中 M*=Homz（M，Q/Z）为 M的特征模。

证明：若右R-模M是GP-平坦右R模，则显然有正合列 0→Rrn→R， 有 0→M⊗Rrn→M⊗R正合，由于Q/Z是内射余生成子，那么

反之，我们继续考虑如上的交换图，这时，右列是正合的，得出左列是正合的，故每个Mα是GP-平坦模。

命题3 设M，N是GP-平坦模，则M⊗N仍是GP-平坦模。

证明：取m为一个足够大的自然数，则对于任一自然数n≥m，

因为 α，γ 同构，若 x∈ker β，则 0=ψβ（x）=γτ（x），则 τ（x）=0，因为 γ 是单的，且两行正合，则有x=σ（y），对某个 y∈A⊗Rrn。 但这样 0=β（σ（y））=φ（α（y））可得 α（y）=0（φ 单）。 这样 y=0，x=σ（y）=0可得β同构，由定义B是GP-平坦模①短正合列中的三个模有着一定的联系，命题4给出了前后两模的GP-平坦性决定了中间模的GP-平坦性，我们自然会思考其它条件的GP-平坦性，尤其是中间模的GP-平坦性能否决定前后两端模的GP-平坦性，如不行，需要在什么条件下才能成立，为此我们首先引入纯子模的定义。。

称φ（A）是B的纯子模。

引理1[10-11]对右R-模M来说，下列条件等价：

（1）M是绝对纯的.

（2）M 是 E（M）的纯子模（E（M）为 M 的内射包）.

（3）M 是 FP-内射模.

（4）M是FP-内射模的纯子模.

引理2 设R是任意环，对右R-模M来说，下列条件等价：

（1）M 是 GP-平坦模；

（2）对任意环R，存在m∈N，使得任意的n≥m，n∈N，有 Tor1R（M，R/Rrn）=0。

命题5 设0→AR→BR→CR→0是纯正合列，若B是GP-平坦模，则A和C都是GP-平坦的。

证明：对于任意环R，存在m∈N，使得任意的n≥m，n∈N，由长正合列有

定理1 对于环R，下列条件是等价的：

（1）GP-平坦模的直积是GP-平坦的；

（3）环R是左GP-凝聚环；

（4）左R-模M是GP内射的，当且仅当 M*是GP-平坦的；

（5）左R-模M是GP内射的，当且仅当 M**是GP内射的；

（6）右R-模M是GP-平坦的，当且仅当 M**是GP-平坦的；

（7）对于任意环 S，

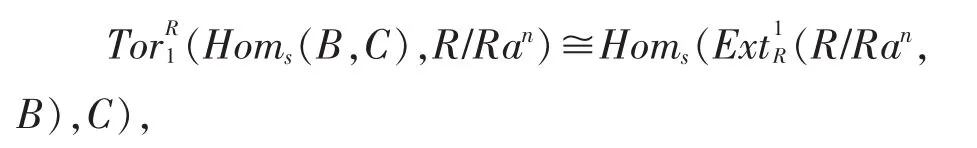
其中n为某一个固定常数后任一自然数，B为（R，S）-双模，CS是内射的。

证明：（1）⇔（2）显然。

（3）⇔（1） 设{Mi|i∈I}是一簇 GP-平坦模，要证∏i∈IMi也是GP-平坦模，由定理3知，我们只需证 α：（∏i∈IMi）⊗Rrn→（∏i∈IMi）Rrn是单的。 考虑如下交换图：

由（3）知Rrn是有限表现的，所以ε是同构，且β也是同构，又{Mi|i∈I}是一簇GP-平坦模，则得 γi：Mi⊗Rrn→MiRrn是单的， 所以 γ 是单的，从而知α是单的，那么∏i∈IMi是GP-平坦模。

（3）⇔（7） 见引理 3。

（7）⇔（4） 令 S=Z，C=Q/Z，B=M，则由条件知有

所以左R-模M是GP内射的，当且仅当 M*是GP-平坦的。

（4）⇔（5） 设左R－模M是GP内射的，则由所给条件知，M*是GP-平坦模，从而M**是GP内射的，反之显然。

（5）⇔（6） 如果 M 是 GP-平坦模，则 M*是GP内射的，由所给条件知M***是GP内射的，从而M**是GP-平坦模。反之，若M**是GP-平坦模，由引理1知M是M**的纯子模，所以M是GP-平坦模。

2 GP-平坦维数

下设环R为交换环，由于每个R-模M都有平坦分解，而平坦模是GP-平坦模，所以每个R-模都有GP-平坦模，即存在正合列

则在M的所有这种形状的GP-平坦分解中，必有一个GP-平坦分解，其中的非负整数n是最小的，这个最小的n称为R-模M的GP-平坦维数，记为Gfd（M）=n，若上述的 n不存在，则记为Gfd（M）=∞。 记 Gfd（R）=sup{Gfd（M）|M 为任意的R-模}为环R的GP-平坦维数；WD（R）为环R的整体维数。并由定义，不难得出如下结论①（1）Gfd（R）≤WD（R），对任意的环 R；（2）若 R 是遗传环，则有 Gfd（R）≤1；（3）若 R 是 Von Nenmann 正则环，则 Gfd（R）=0。。

命题6 R-模是GP-平坦模当且仅当Gfd（M）=0。

证明：设M是GP-平坦模，则M有GP-平坦分解 0→…→0→F0→M→0， 其中 F0=M，Fi=0，∀i≥1，那么 Gfd（M）=0。 反之，设 Gfd（M）=0，则 M有一个GP-平坦分解…→0→F0→M→0，其中Fi=0，∀i≥1，因此，F0≅M，故 M 是 GP-平坦模。

命题7 Gfd（M）≤1当且仅当GP-平坦模的子模是GP-平坦模。

证明：对任意右 R-模 M，有 Gfd（M）≤1，设 F0是GP-平坦模，F1是F0的子模，则有正合列0→F1→F0→F0/F1→0，由于已知 Gfd（F0/F1）≤1，则有F1是GP-平坦模。反之，设M是任意右R-模，则有自由模F0，使正合列0→F1→F0→M→0成立，由于F0是GP-平坦模，由已知F1也是GP-平坦模，得 Gfd（M）≤1。

类似于GP-平坦模，由于每个R-模M都有内射分解，而内射模是GP-内射模，可定义GP-内射维数的定义，并刻画两者之间的关系。

设R-模M有如下形状的GP-内射分解

则在M的所有这种形状的GP-内射分解中，必有一个GP-内射分解，其中的非负整数n是最小的，这个最小的n称为R-模M的GP-内射维数，记为Gid（M）=n，若上述的 n不存在，则记为Gid（M）=∞。

定理2 设R是一个环，对任意的R-模M，Gfd（M）=Gid（M*）。

证明：设 M 是任意 R-模，Gfd（M）=n，由 GP-平坦分解的定义知，存在一个正合列

众所周知，若每一个R-模都是平坦模，则R称为正则环；若每一个内射R-模都是平坦模，则称R称为IF环。可以说，近几十年来，正则环和IF环一直国内外环论专家关注的焦点，尤其在历届的中日韩环论国际会议上，一直是讨论的热点。我们现在利用GP-平坦性做一下推广，可以得到一些平行的结论。若每一个R-模都是GP-平坦模，则称R称为GP－正则环；若每一个内射R-模都是平坦模，则称R称为IGPF环②环R是正则环当且仅当环R是GP-正则环，并且GP-平坦模的子模都是平坦模。事实上，对于任意的R-模F，存在正合列0→F→F′，根据题设R是GP-正则环，那么由定义知F、F′为GP-平坦模，又由题设GP-平坦模的子模都是平坦模知F是平坦模，因此R是正则环，反之显然。。

结合文献[12]，类似于文献[13]的证明，我们可以得到如下命题

定理3 设R为一任意环，则下述等价：

（1）R 为 GP-正则环；

（2）内射R-模的本质子模是GP-平坦模；

（3）GP-平坦R-模的同态像是GP-平坦模；

（4）任意R-模的两个GP-平坦子模的和是GP-平坦模；

（5）任意R-模的两个同构的GP-平坦子模的和是GP-平坦模。

定理4 设R为一任意环，则下述等价：

（1）R 为 IGPF 环；

（2）FP－内射R-模Q的都是GP-平坦模；

（3）若 Q1⊂Q 都是 FP－内射 R-模，则 Q/Q1是GP-平坦模；

（4）对任意的 R-模 M，E（M）是 GP-平坦模；

（5）任意的R-模M是GP-平坦模的子模；

（6）内射R-模M是GP-平坦模的子模。

证明：（1）⇔（2） 因为 FP－内射模Q是内射包 E（Q）的纯子模，根据题设知 E（Q）是 GP－平坦模，由命题5知Q是GP－平坦模。

（2）⇔（3） 显然 0→Q1→Q→Q/Q1→0 是纯正合列，而Q1是FP－内射模，Q是GP－平坦模，所以由命题5知Q/Q1是GP-平坦模。

（1）⇔（4）⇔（5）⇔（6） 显然成立。

（6）⇔（1） 设M为任一内射模，M为F的子模且F为GP－平坦模，则存在正合列0→F→M，由命题2知M是GP-平坦模，即证R为IGPE环。

（3）⇔（1） 任一内射模M是FP－内射模，而0模也是FP－内射模，因此有条件知M=M/0是GP－平坦模，即证R为IGPE环。

由定理4不难得出，环R是IF环当且仅当环R是IGPE环，并且GP－平坦模的每个内射子模都是平坦模。