一种新型四轴飞行器姿态角控制方法与仿真

孙春虎 方愿捷 王 静 李昊东

（巢湖学院 电子工程学院，安徽 巢湖 238000）

0 引言

四轴飞行器姿态角系统的数学模型是个非线性、强耦合、多变量的欠驱动系统。四轴飞行器控制常采用卡尔曼滤波加单级PID控制，但是存在卡尔曼滤波噪声偏大，滞后略微严重，单级PID难操作，打舵响应慢，跟随效应差的缺点。为此，文章在研究四轴飞行器姿态角数学模型的基础上，提出了一种新型姿态角控制方法，并以滚转角、偏航角控制为例，对新型控制系统进行了Simulink仿真，仿真结果验证了控制方法的可行性，具有一定的参考和应用价值[1-3]。

1 四轴飞行器姿态角数学模型分析

四轴飞行器姿态角的数学模型是个多变量、非线性、强耦合的复杂系统。依据文献[4]，利用拉格朗日方程可求得姿态角的一般简化数学模型如公式（1）所示[5]。

式中，φ、θ、ψ 分别表示滚转角、俯仰角、偏航角；IX、IY、IZ分别表示绕X轴、Y轴、Z轴的转动惯性常量；l表示旋翼中心到机体中心的距离；U2、U3、U4分别表示滚转通道控制输入量、俯仰通道控制输入量、偏航通道控制输入量。

应用小扰动原理将非线性方程线性化处理，并忽略附加小扰动后，公式（1）可简化为[6-7]

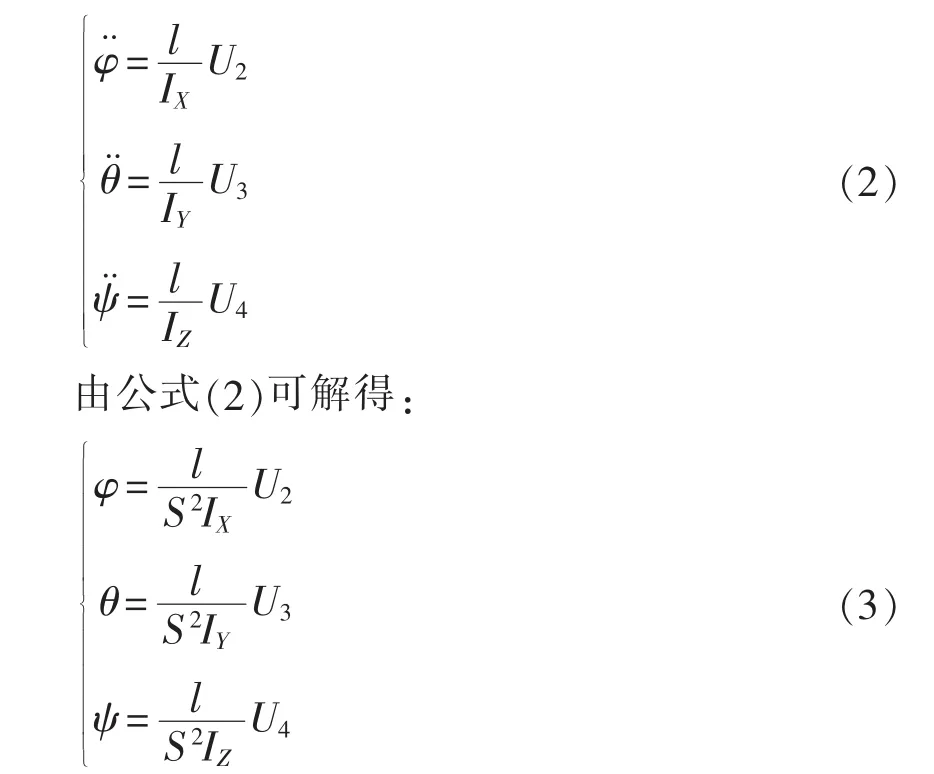
从公式（3）可以看出，滚转角φ输出与控制量U2有关；俯仰角θ输出与控制量U3有关；偏航角ψ输出与控制量U4有关。

2 四轴飞行器姿态角控制策略研究

由于滚转角通道、俯仰角通道、偏航角通道控制对象数学模型类似，下面只以偏航角ψ控制为例，对偏航角ψ控制系统进行分析和设计。由公式（3）可知，偏航角ψ输出对输入控制量U4的传递函数为二阶积分环节。因此，可以将偏航角ψ控制系统校正成典型Ⅰ型系统，再利用常规PID调节器即可实现偏航角控制。偏航通道控制系统如图1所示,它主要由外环PID调节器部分和内环对象校正部分组成[8-9]。

图1 偏航通道控制系统

由图1可求得：内环对象校正系统闭环传递函数变为

由公式（4）可以看出，此时控制对象为典型控制对象，外环PID控制只需采用比例控制器，无需采用积分和微分控制。假设比例控制器比例系数为Kψ，则图1偏航通道控制系统的闭环传递函数可表示为

3 四轴飞行器姿态角控制系统仿真

笔者在实验室所设计的四轴飞行器测得的参数如表1所示。

表1 飞行器参数表

将表 1 中数据代入公式（8）、（9）、（10）可解得，比例系数 Kφ=Kθ=53.13，Kψ=2.36，滚转与俯仰通道的传递函数均为106.26/S2，偏航通道的传递函数为4.72/S2。

3.1 新型控制策略控制效果仿真

3.1.1 滚转角通道仿真

根据新型滚转角控制策略，所搭建的滚转角通道Simulink仿真模型[10-11]如图2所示。

图2 滚转角通道仿真模型

图中常量1为滚转角给定值，单位弧度；K表示滚转通道比例系数，值为53.13；106.26/S2为滚转通道对象传递函数；du/dt为微分环节；内环为对象校正闭环系统；外环为比例控制闭环系统；仿真时间为1 s。

滚转角通道仿真结果如图3所示。

图3 滚转角通道仿真结果

滚转角给定1 rad时，滚转通道输出能稳定在1 rad输出；系统能在0.1 s的时间内实现系统的快速稳定；超调量为2.3%，超调量小；稳态误差小，精度高。

3.1.2 俯仰角通道仿真

根据新型俯仰角控制策略，所搭建的俯仰角通道Simulink仿真模型[10-11]如图4所示。

图4 俯仰角通道仿真模型

图中常量0.5为俯仰角给定值，单位弧度；K表示俯仰通道比例系数，值为53.13；106.26/S2为俯仰通道对象传递函数；du/dt为微分环节；内环为对象校正闭环系统；外环为比例控制闭环系统；仿真时间为1 s。

俯仰角通道仿真结果如图5所示。

图5 俯仰角通道仿真结果

俯仰角给定0.5 rad时，滚转通道输出能稳定在0.5 rad输出；系统能在0.1 s的时间内实现系统的快速稳定；超调量为1%，超调量小；稳态误差小，精度高。

3.1.3 偏航角通道仿真

根据新型偏航角控制策略，所搭建的偏航角通道Simulink仿真模型如图6所示。

图6 偏航角通道仿真模型

偏航角通道的仿真结果如图7所示。

图7 偏航角通道仿真结果

偏航角给定1 rad时，偏航通道输出能稳定在1 rad输出；系统能在1 s的时间内实现系统的快速稳定；超调量为4.2%，超调量小；稳态误差小，精度高。

3.2 新型控制策略抗干扰效果仿真

3.2.1 滚转角通道仿真

采用新型控制策略，外加干扰时，滚转角通道抗干扰仿真模型如图8所示。

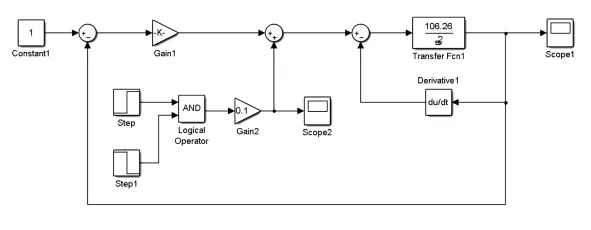
图8 滚转角通道抗干扰仿真模型

图中step模块、step1模块为阶跃信号；AND模块为与门；Gain1、Gain2 为比例模块；step、step1经过AND门后得到一脉冲信号；脉冲信号经过Gain2模块衰减到0.1倍，得到一干扰信号；干扰信号在5～8 s期间起作用，幅值为0.1 rad；其他时间段干扰信号不起作用，幅值为0 rad；滚转通道对象传递函数不变，仿真时间为12 s。

根据仿真模型，所得滚转角通道抗干扰仿真结果如图9所示。

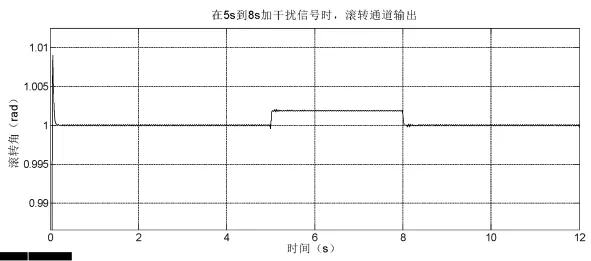
图9 滚转角通道抗干扰仿真结果

从滚转角通道抗干扰仿真结果可以看出，当在5 s时刻加入0.1 rad干扰时，滚转角在6 s时输出稳定不变的1.002 rad，系统仍然稳定，稳态误差为0.2%，抗干扰能力很好；当在8 s时刻撤除干扰时，滚转角又能恢复稳定，抗干扰性恢复能力很好。

3.2.2 俯仰角通道仿真

采用新型控制策略，外加干扰时，俯仰角通道抗干扰仿真模型如图10所示。

图10 俯仰角通道抗干扰仿真模型

图中step模块、step1模块为阶跃信号；AND模块为与门；Gain1、Gain2 为比例模块；step、step1经过AND门后得到一脉冲信号；脉冲信号经过Gain2模块衰减到0.1倍，得到一干扰信号；干扰信号在4～7 s期间起作用，幅值为0.1 rad；其他时间段干扰信号不起作用，幅值为0 rad；俯仰通道对象传递函数不变，仿真时间为10 s。

所得俯仰角通道抗干扰仿真结果如图11所示。

图11 俯仰角通道抗干扰仿真结果

从俯仰角通道抗干扰仿真结果可以看出，当在4 s时刻加入0.1 rad干扰时，滚转角在5 s时输出稳定不变的0.502 rad，系统仍然稳定，稳态误差为0.4%，抗干扰能力很好；当在7 s时刻撤除干扰时，俯仰角又能恢复稳定，抗干扰性恢复能力很好。

3.2.3 偏航角通道仿真

同理，采用新型控制策略，外加干扰时，所得偏航角通道抗干扰仿真模型如图12所示。偏航通道对象传递函数不变，仿真时间为12 s。

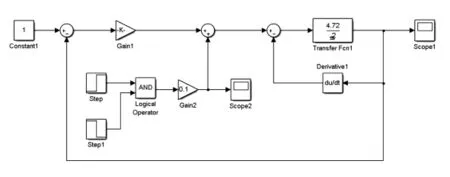
图12 偏航角通道抗干扰仿真模型

根据仿真模型，所得偏航角通道抗干扰仿真结果如图13所示。

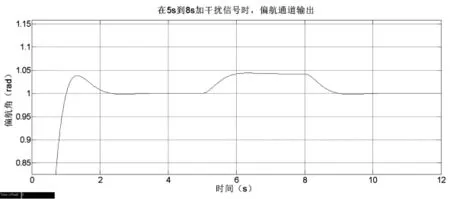
图13 偏航角通道仿真模型

从偏航角通道抗干扰仿真结果可以看出，当在5 s时刻加入0.1 rad干扰时，偏航角在6 s时输出稳定不变的1.043 rad，系统仍然稳定，稳态误差为4.3%，抗干扰能力较好；8 s时刻撤除干扰，9 s时刻之后，偏航角又能恢复稳定，抗干扰性恢复能力较好。

3.3 新型控制策略在控制对象发生变化时控制效果仿真

3.3.1 滚转角通道仿真

当滚转角通道控制对象变化时，新型控制策略控制效果仿真模型如图14所示。

控制对象变化前，滚转角通道传递函数为106.26/S2，控制对象变化后，滚转角通道传递函数为80/S2，仿真时间为20 s。

图14 滚转角通道控制对象变化时仿真模型

图中step2模块、step3模块、AND模块、NOT模块组成了一脉冲控制信号；脉冲控制信号在13 s到17 s时间段输出低电平0；脉冲控制信号在其他时间段输出高电平1；当脉冲控制信号为1时，Switch模块选中106.26/S2为控制对象；当脉冲控制信号为0时，Switch模块选中80/S2为控制对象。

根据仿真模型，所得滚转角通道对象变化时仿真结果如图15所示。

图15 滚转角通道控制对象变化时仿真结果

根据滚转角通道控制对象变化时仿真结果可以看出：在13 s时刻当控制对象由106.26/S2变为80/S2时，系统开始自动调节，14 s时系统稳定，输出0.9999 rad，稳态误差为0.01%；在17 s时刻当控制对象由80/S2恢复为106.26/S2时，系统开始自动调节，18 s时系统稳定，输出1.0001 rad，稳态误差也为0.01%。

3.3.2 俯仰角通道仿真

当俯仰角通道控制对象变化时，新型控制策略控制效果仿真模型如图16所示。

控制对象变化前，俯仰角通道传递函数为106.26/S2，控制对象变化后，俯仰角通道传递函数为80/S2，仿真时间为20 s。

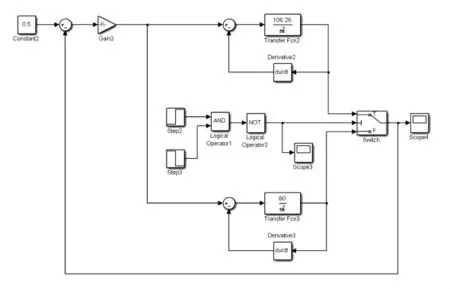
图16 俯仰角通道控制对象变化时仿真模型

图中step2模块、step3模块、AND模块、NOT模块组成了一脉冲控制信号；脉冲控制信号在12～16 s时间段输出低电平0；脉冲控制信号在其他时间段输出高电平1；当脉冲控制信号为1时，Switch模块选中106.26/S2为控制对象；当脉冲控制信号为0时，Switch模块选中80/S2为控制对象。

根据仿真模型，所得俯仰角通道对象变化时仿真结果如图17所示。

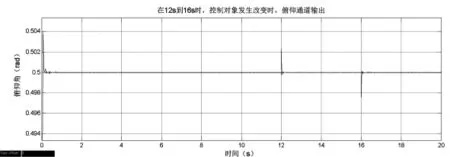
图17 俯仰角通道控制对象变化时仿真结果

根据俯仰角通道控制对象变化时仿真结果可以看出：在12 s时刻当控制对象由106.26/S2变为80/S2时，系统开始自动调节，13 s时系统稳定，输出0.4999 rad，稳态误差为0.02%；在16 s时刻当控制对象由80/S2恢复为106.26/S2时，系统开始自动调节，17 s时系统稳定，输出0.5001 rad，稳态误差也为0.02%。

3.3.3 偏航角通道仿真

当偏航角通道控制对象变化时，新型控制策略控制效果仿真模型如图18所示。

控制对象变化前，偏航角通道传递函数为4.72/S2，控制对象变化后，偏航角通道传递函数为3/S2，仿真时间为 20 s。

图18 偏航角通道仿真模型

根据仿真模型，所得偏航角通道对象变化时仿真结果如图19所示。

图19 偏航角通道仿真结果

如图，在13 s时刻当控制对象由4.72/S2变为3/S2时，系统开始自动调节，14 s时系统稳定，输出0.9999 rad，稳态误差为0.01%；在17 s时刻当控制对象由3/S2恢复为4.72/S2时，系统开始自动调节，18 s时系统稳定，输出0.9997 rad，稳态误差为0.03%。

4 结论

研究分析了四轴飞行器的姿态角数学模型，并得到了简化的数学模型。针对所得的姿态角数学模型，提出了一种四轴飞行器姿态角新型控制策略，最后对新型姿态角控制系统进行了Simulink仿真，仿真结果表明：所设计控制策略的正确性；能对俯仰角通道、滚转角通道和偏航角通道进行较好的控制。所设计的新型四轴飞行器控制系统具有一定的参考与应用价值。