二元(p,q)-Bernstein-Schurer-Kantorovich 算子的逼近
查星星 刘相国 王晓燕
(巢湖学院 数学与统计学院,安徽 巢湖 238000)
0 引言
对于正线性算子逼近问题的研究一直以来深受众多学者们青睐。人们在研究正线性算子的过程中,关注一元算子逼近问题的同时提出二元或多元算子的逼近,得到了大量二元算子逼近的相关理论。如在1995年,薛银川[1]构造出了二元Baskakov算子,讨论了算子在C空间的逼近问题;1998 年,二元 Mirkyan-Szász算子[2]被 Lucyna R、Mariola S提出,并在不同空间里研究了该算子加权逼近定理。其后,由于q微积分的不断发展且被引用于逼近理论,于是,大量q型二元算子被逐一挖掘,如二元q-Bernstein算子[3]、二元q-Bernstein-Schurer-Kantorovich算子[4]、二元 q-Bernstein-Schurer-Durremeyer算子[5]等。
当q型算子逼近性质被充分研究后,(p,q)微分学开始步入逼近论。2015年,Mursaleen在q-Bernstein算子的基础上提出 (p,q)-Bernstein算子[6],推广了q-Bernstein算子的相关性质。自此,有关于(p,q)型算子呈现于世人面前。2016年,Sidharth1 M.与Agrawal P.N.在文献[7]中介绍了二元(p,q)-Bernstein-Schurer算子并讨论了其逼近性质;同年 Acar在文献[8]中构建了二元(p,q)-Bernstein-Kantorovich算子并得到该算子一些的逼近结论。由此可知,关于(p,q)型二元算子逼近问题的研究正在持续发展中。本研究主要在一元(p,q)-Bernstein-Schurer-Kantorovich 算子[9]的基础上构造二元(p,q)Bernstein-Schurer-Kantorovich算子,验证该算子的一些逼近问题,从而更进一步推广一元算子的逼近性质,更加丰富逼近理论的完整性。
1 基础知识及引理
出于证明需要,首先介绍一些基本概念与定义。
设 0 引 理 4 设 0 证明 由该算子为线性算子及引理2的内容易得结论。 这里介绍下文中的记号: 设 δ1>0,δ2>0,,I2=[0,1+m1]×[0,1+m2],m1∈N,m2∈N,f∈C(I2),则关于二元函数f的连续模定义如下: 本研究主要在一元(p,q)-Bernstein-Schurer-Kantorovich算子的基础上构造出二元算子,介绍该算子的一些逼近性质,进而推广了前人的逼近结论。


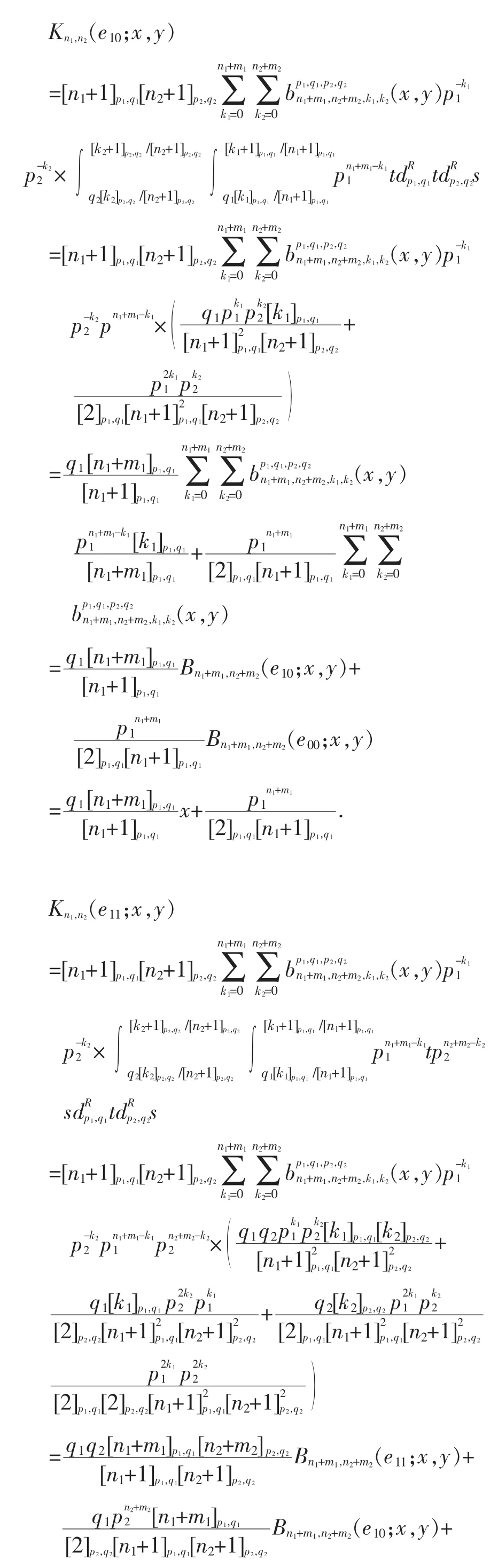

2 主要结果


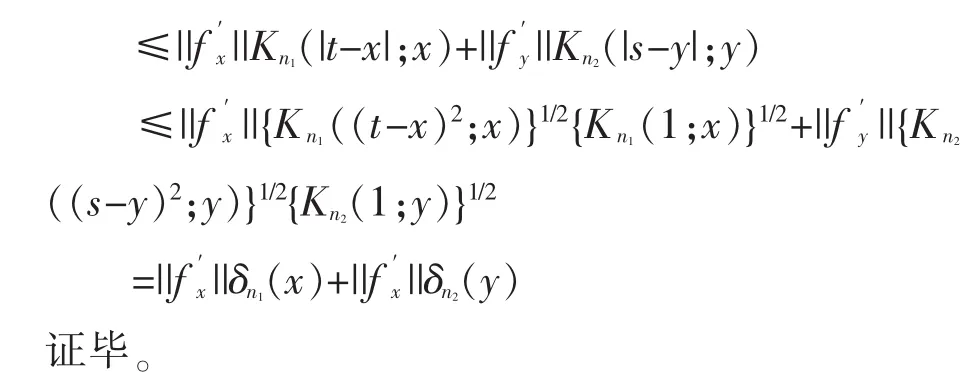
3 结语

