吸血蝙蝠与牛群间狂犬病毒的传播研究

张菊平，李 丹

(1.山西大学 复杂系统研究所， 太原 030006；2.疾病防控的数学技术与大数据分析山西省重点实验室， 太原 030006)

狂犬病是由狂犬病毒引起的人和其他所有哺乳动物的急性致死性中枢神经系统的自然疫源性疾病，病死率高，呈全球性分布，是世界上最致命的传染病之一[1-2]。该病只通过唾液、血液传播，潜伏期内不传播,也不母婴传播。吸血蝙蝠[3-5]是狂犬病病毒的自然宿主,其体型小，一次生产一胎，平均寿命为12年。吸血蝙蝠传播狂犬病毒的方式为以下4种[5]：① 吸食动物血液；② 抓伤动物；③ 吸血蝙蝠呼出的大量气溶胶传播；④ 口腔感染(常见于蝙蝠种内传播)。吸血蝙蝠主要通过吸食动物或人的血液来传播狂犬病毒，是狂犬病在动物和人之间传播的重要媒介之一。牛狂犬病的发病牛以犊牛和母牛较多见，该病常在一个地区内散发，潜伏期平均30～90 d，病程3～7 d。

近年来吸血蝙蝠传播致命的狂犬病毒越来越引起人类重视。比如在1996年,WARNER等[6]从秘鲁的两例致命病例脑组织样本中测试证实样本中存在的狂犬病毒与吸血蝙蝠所携带的最为接近。ARELLANO-SOTA等[7]对秘鲁的阿普里马克省调查发现，2014年有505～724 头牛被蝙蝠噬咬而感染狂犬病致死，造成巨大经济损失。为有效控制吸血蝙蝠狂犬病毒的传播，在阿根廷和墨西哥进行的试验中证明接种疫苗可以有效保护牲畜免受狂犬病毒的侵害[8]。Streicker等[9]对秘鲁的4个地区的20个吸血蝙蝠种群进行纵向捕获-重新捕获研究， 发现幼年和次成年吸血蝙蝠体内所含血清阳转率最高，所以重点捕杀成年蝙蝠可以减缓狂犬病毒的传播。

本文以吸血蝙蝠与牛间的相互关系为基础，建立数学模型，求得系统的阈值并分析了平衡点的稳定性，针对系统中牛群免疫率参数进行了敏感性分析，最后给出控制狂犬病毒传播的预防措施。

1 建立模型

根据吸血蝙蝠与牛群间狂犬病毒传播机制做如下假设：① 忽略牛群间狂犬病毒的传播；② 蝙蝠潜伏期和发病期的病毒累积量不同，假设血清阳转率不同；③ 养牛场每年均会引入一批牛犊来保持数量的恒定，假设牛群有常数输入，指数输出。 狂犬病毒在吸血蝙蝠与牛群间的传播流程如图1所示。

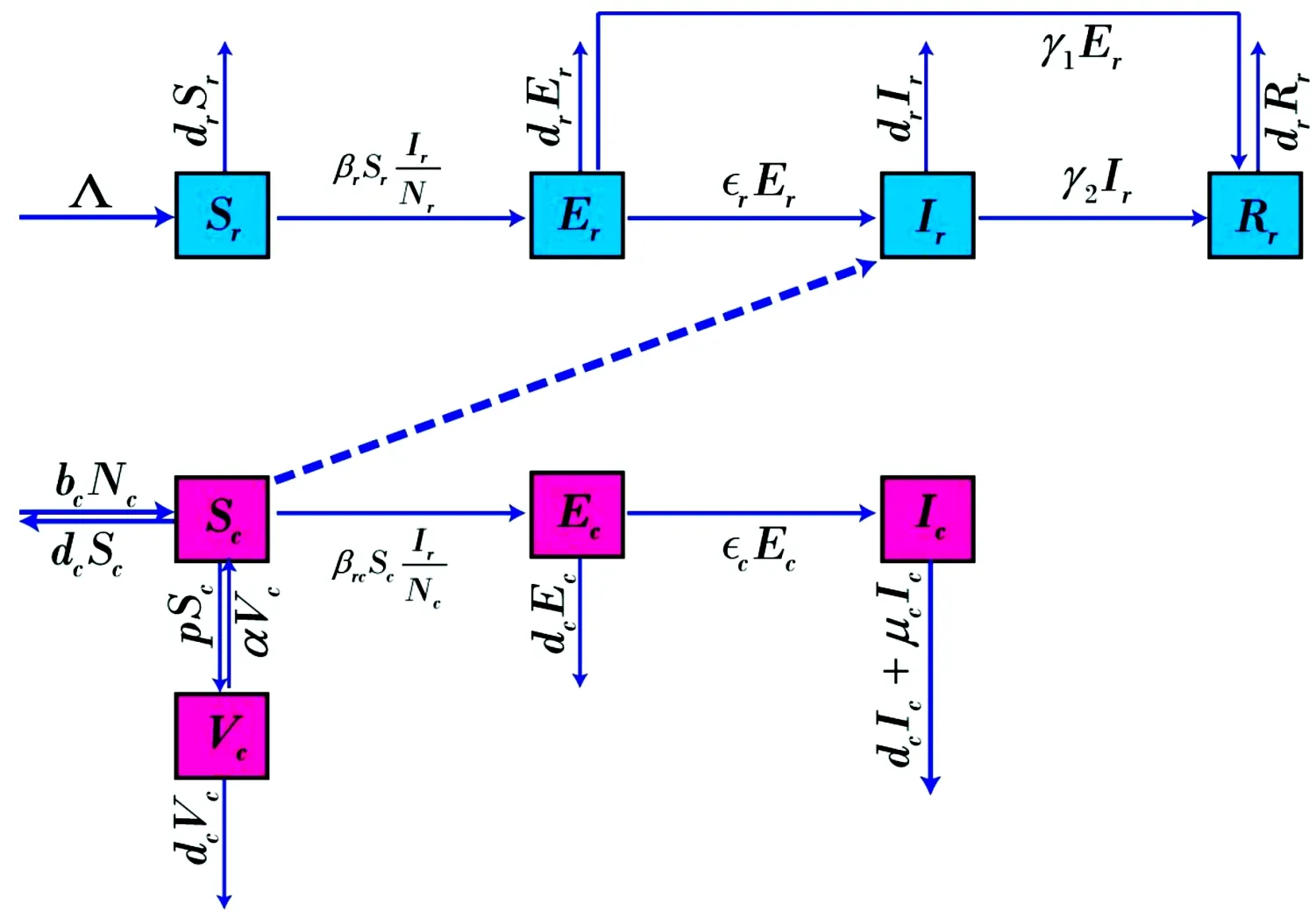
图1 吸血蝙蝠与牛狂犬病毒传播流程

流程图中参数说明：记吸血蝙蝠群体总量为Nr=Sr+Er+Ir+Rr,其中Sr、Er、Ir、Rr分别表示易感者、潜伏期、染病者和恢复者吸血蝙蝠，吸血蝙蝠的出生率和死亡率分别为br和dr,且br=dr,发病蝙蝠感染易感蝙蝠的传染率为βr,潜伏期到发病期的转化率和血清阳转率为εr和γ1，发病期的阳转率为γ2。Sc、Ec、Ic、Vc分别表示易感者、潜伏期、染病者和接种者牛。记牛群总数为Nc=Sc+Ec+Ic+Vc；牛的输入为Λ；死亡率和因病死亡率为dc和μc；牛从潜伏期到发病期的转化率为εc；发病蝙蝠感染易感牛的传染率为βc；接种免疫率和免疫失效率分别为p和α。

根据传播流程建立相应的动力学模型如下：

(1)

2 模型分析

2.1 吸血蝙蝠模型稳定性分析

由于模型(1)的前4个方程和后4个方程独立，且满足Nr=Sr+Er+Ir+Rr，因此将前4个方程降维归一化得：

(2)

系统(2)的正向不变集为

Γr={(sr,er,ir)∈R3∣0≤sr,

er,ir≤1,sr+er+ir≤1}

系统(2)的无病平衡点为P0(1,0,0)，根据下一代矩阵理论[10]得

故系统(2)的阈值为

定理1 当Rr0<1时，无病平衡点P0是全局渐近稳定的。

证明由于sr≤1，可得系统(2)的辅助系统为

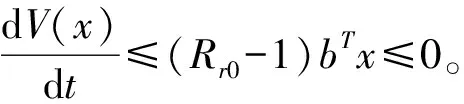
定理2 当Rr0>1时，系统(2)的无病平衡点不稳定，存在唯一的正平衡点P*且全局渐近稳定的。

(3)

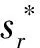
从而，当Rr0>1时，系统(2)存在唯一的正平衡点为：

系统(2)在P*点处的Jacobian矩阵为

其特征方程为λ3+a1λ2+a2λ+a3=0,其中:

a1=brRr0+(γ1+εr+dr)+(γ2+dr)>0

a2=brRr0(γ1+εr+2dr)+

2(γ1+εr+dr)(γ2+dr)>0

a3=brRr0(γ1+εr+dr)(γ2+dr)+

且a1a2-a3>0。根据Hurwitz判据得矩阵的特征根均具有负实部，故正平衡点P*局部渐近稳定。

给出系统(2)的Jacobian矩阵对应的第二加性复合矩阵：

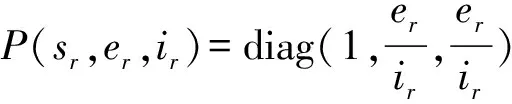
令B=PfP-1+PJ[2]P-1并写成如下分块矩阵

其中：

B11=-βrir-2dr-γ1-εr

设(u,v,w)∈R3，定义R3中的向量范数P.P如下：

||(u,v,w)||=max{|u|,|v|,|w|}

记μ(B)是范数P.P的Lozinskl测度,用估值方法得μ(B)≤sup{g1,g2},其中:

g1=μ1(B11)+∣B12∣

g2=μ1(B22)+∣B21∣

μ1(B11)=-βrir-2dr-γ1-εr,

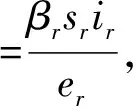
(γ2+2dr+γ1+εr)}

从而得

将式(2)中的第2和第3方程代入上式可得

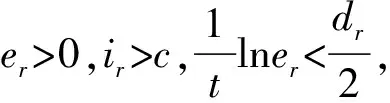
因此系统(2)的正平衡点全局渐近稳定。

2.2 牛群模型稳定性分析

关于牛群的模型如下：

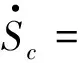
α(Nc-Sc-Ec-Ic)

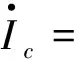
Λ-dcNc-μcIc

上述系统的正向不变集为

Γc={(Sc,Ec,Ic,Vc)∈

由定理2知：当Rr0>1时，蝙蝠系统中存在唯一稳定的正平衡点，所以仅考虑系统的正平衡点。

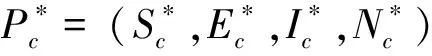
a=μc(p+dc+α)(dc+μc)(dc+εc)>0

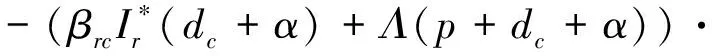
(dc+μc)(dc+εc)<0

根据牛群中正平衡点存在性可得如下阈值

当Rc0=1时，系统仅有1个正平衡点为：

当Rc0>1时，系统有两个正平衡点：

2.3 系统(1)整体分析

根据下一代矩阵理论，系统(1)在无病平衡点处的基本再生数为

因此，吸血蝙蝠对牛群间狂犬病毒的传播起决定性作用。当吸血蝙蝠中的基本再生数Rr0<1时，狂犬病不会在牛群中传播；当Rr0>1且Rc0≥1时，狂犬病会在牛群间传播，且形成地方病。

3 数值模拟

现阶段控制狂犬病在牛群间传播的最有效措施是给牛群接种疫苗，模拟中取参数γ1=0.05,br=dr=0.01,γ2=0.08,α=0.35,βrc=0.34,βr=0.89,εr=0.9,εc=1,μc=1,Λ=1 000时，对牛接种覆盖率进行敏感性分析，结果见图2。

图2 不同接种率对牛群狂犬病传播的影响

从图2中可以看出：当p=0时，狂犬病会在牛群中迅速流行；当采取接种疫苗措施后，染病牛的数量明显减少。另外，考虑疫苗在牛体内1～1.5年后会失效以及接种疫苗所需成本问题，从图2可以看出当免疫覆盖率≥70%时，染病牛的数量变化趋势几乎一致。

4 结论

本文以吸血蝙蝠和牛群间狂犬病毒的传播机理建立数学模型，获得了模型的阈值并分析了平衡点的稳定性。根据对模型的整体分析知，牛群中狂犬病毒的传播中吸血蝙蝠起决定性作用。当Rr0>1,Rc0≥1时，狂犬病毒会在牛群中传播并形成地方病。为降低牛群中狂犬病毒传播的危害及经济方面损失，通过对参数敏感性分析可知，当疫苗覆盖率达到70%以上，可有效预防牛群中狂犬病毒的传播。