Win Ratio法在比较两组生存资料复合终点数据中的应用*

李 超 梁煊怡 康轶君 朱 妮 Tao Chen Duolao Wang△ 颜 虹△

【提 要】 目的 介绍Win Ratio法在比较两组生存资料复合终点数据的基本原理及方法。方法 以一项采用整群随机化双盲对照设计的孕期营养素干预研究为实例，运用Win Ratio法分析比较不同营养素补充对子代两种复合结局“孕28周至分娩后4周死亡”及次要不良结局“低出生体重”的影响，并运用Bootstrap法计算95%CI。比较Win Ratio法及传统Cox风险回归模型计算结果间的差异。结果 Win Ratio法与传统Cox风险回归所得结果一致，两组间差异均无统计学意义。Win Ratio法分析结果显示对照组(孕期补充叶酸)的不良结局发生率是干预组(孕期补充多维营养素)的1.07倍，95%CI为(0.85，1.27)；传统Cox风险回归模型分析的结果与Win Ratio法相似，即对照组的不良结局发生是干预组的1.04倍，95%CI为(0.83，1.31)。结论 相较于传统的生存分析，Win Ratio法在分析多种结局的生存资料时，可考虑结局间的重要性，同时在保证良好的准确性和检验效能的前提下完成对生存资料的区间估计及干预效应的评价。

在医学随访研究中，常通过收集时间-事件数据对两个变量对象的结局情况进行观察研究，从而评价某种干预的效果。目前常用生存分析的相关方法来解决此类问题，应用最多的方法是通过拟合Cox风险回归模型进行组间比较，并通过计算风险比(HR值)及其95%CI评价干预效应。但临床医学研究中，结局变量常由多种结果综合定义，在各结果成分具有优先级顺序的研究中，Cox风险回归无法区分各结果的主次顺序，从而可能导致分析结果难以解释。除此之外，Cox风险回归依赖于严格的模型假定条件，要求必须满足比例风险假定(PH假定)，导致其在实际应用中具有一定的局限性[1-3]。本文所介绍的Win Ratio法则可以很好地解决上述问题，不仅可以对生存资料进行组间比较、评价干预效应并估算其95%CI(Bootstrap法)，还能对多种结局变量划分优先顺序后进行分析，从而减少因各结果成分意义不对等而对研究结论产生的影响。由于目前国内尚未出现将Win Ratio法应用于复合终点生存资料分析的报道，故在此对该方法作介绍，愿更多科研工作者能够从中获益。

原理与方法

1.Win Ratio法的应用

本课题组已系统介绍了Win Ratio法的原理[4]。简单来说，Win Ratio法以每组研究对象中被称为“winner”和“loser”的频数作为数据分析的基础，winners定义为在两组研究对象间可能出现的所有配对情况中干预组的干预效果优于对照组的总频数NW；losers定义为两组研究对象间所有干预组的干预效果劣于对照组的总频数NL；干预组与对照组干预效果相当的总频数NT定义为tied[5-6]。

应用该方法分析生存资料的原理与先前所述一致，但具体输赢判定标准有所不同。在比较两组非正态分布数据时，定义结局变量数值大的一方为winner，结局变量数值小的一方为loser；在对生存资料中的单个结局变量进行两组间比较时，以干预组在一定时间内观察到特定结局，而对照组未进一步出现与干预组一致或更优的结局为标准(如对照组出现特定结局时间晚于干预组、对照组在干预组出现特定结局后中途失访或对照组在研究结束时均仍未发生特定结局)，判定该干预组研究对象为winner，对照组为loser；同理，若对照组在一定时间内出现特定结局而干预组未进一步出现一致或更优结局，则判定该对照组研究对象为winner，干预组为loser；若在上述两种假定下出现有更优结局的情况(如一组在一定时间内出现特定结局而另一组在前组出现特定结局之前中途失访)，或干预组和对照组在一定时间内均未观察到特定结局(如两组均中途失访或两组均在研究结束时仍未发生特定结局)，即两组干预效果相当，判定为tied[7](图1)。

若两组生存资料的结局变量由具有不对等意义的多个结果成分组成，需先依照优先级为多种结局变量进行排序，按照从最主要结局(最具临床意义的结局成分)至最次要结局(临床意义最小的结局成分)的顺序进行分析，每层结局的输赢判定标准与单个结局变量的生存资料相同(图1)。需要注意的是，若两组对象在上一结局判定中表现为tied，则转而比较下一结局，直至得出“干预组win”、“对照组win”、或在最次要结局水平得出“tied”这三种结论中的任一种为止，且一组win同时表示另一组lose[8]。

图1 单个结局变量的生存资料数据Win-lose判断标准

Win Ratio法评价干预效应的指标为RW值(RW=NW/NL)，前期文章中也已对该指标做以详细说明。在可能出现的所有配对中，干预组的干预效果优于对照组的概率为[RW/(RW+1)]。

2.Win Ratio法的统计推断

其假设检验为H0：RW=1，两组间winner的总频数相等，差别无统计学意义；H1：RW≠1，两组间winner的总频数不等，差别有统计学意义[5-6]。在此依旧采用Bootstrap法对所得RW值进行区间估计，求得RW值的95%CI。即在原始数据经验分布的基础上作有放回的重复随机抽样(要求重复抽样次数大于1000次[9-11])。此法估计RW为有偏估计，故需对RW进行对数转换，再经logRW的偏倚校正法[12-13]求得其置信区间。若RW值的95%CI内不包含1，则拒绝原假设，认为两组间winner的频数不等，且差别具有统计学意义，反之接受原假设，差别无统计学意义。本研究所有分析均采用SAS 9.4软件，Win Ratio法分析数据的相关SAS程序可通过查询相应参考文献或联系本文作者获得。

实例分析

以2002年至2006年我国陕西省贫困县孕期营养素补充干预试验为例进一步阐释Win Ratio法在时间序列分析领域中的应用[14]。该孕期营养素补充试验为严格的随机对照双盲设计，于2002年8月至2006年1月间纳入该地区符合条件的孕产妇，在孕期对受试对象分别补充多种微营养素和单纯叶酸，并通过孕期产检的各项指标及分娩后的随访情况进行纵向数据采集分析。该研究以探究不同营养素补充方案对孕产不良结局影响的组间差异为目的，起始时点为末次月经，终点事件可按结局成分的主次顺序划分为主要终点子代死亡(死产及新生儿死亡)和次要终点低出生体重。根据所收集数据可知“多微营养组”1579人，叶酸组1727人，多微营养组子代死亡数87例，低出生体重数57例，平均死亡时间38.70周，平均随访时间43.58周，平均孕周39.77周；叶酸组子代死亡数91例，低出生体重数82例，平均死亡时间37.00周，平均随访时间43.39周，平均孕周39.56周(表1)。假设多微营养组(干预组)总人数为NA，叶酸组(对照组)总人数为NB，则两组所有可能的配对数为NA×NB，且不难得出NA×NB=NW+NL+NT。

表1 两组间数据特征

*：子代死亡包括死产与新生儿死亡；**：平均死亡时间=(子代死亡日期-末次月经日期)/7

基于该干预研究项目，我们所研究的孕产不良结局由主要不良结局“子代死亡”和次要不良结局“低出生体重”组成。在此实例中，由于“子代死亡”(指围生期死亡，包括死胎、死产、新生儿死亡)相较“低出生体重”对家庭及个体的不良影响更为严重，所以本研究中“子代死亡”不良结局程度显然应优先于“低出生体重”，而在其他临床研究中，需根据不同的结局制定相应的优先顺序。假设干预组对象i与对照组对象j配对，i出现子代死亡，而j未在随访时间内观察到特定结局或出现子代死亡时间晚于i，则判定对象i为winner，对象j为loser。再假设干预组对象s与对照组对象t配对，先比较二者子代死亡情况，对象s出现子代死亡，而t先于s未观察到特定结局(如中途失访)或对象s与对象t均未在随访时间内观察到特定结局，即二者作用效果相当(undecided)，转至比较二者新生儿低出生体重情况，若s出现低出生体重，而t未在随访时间内观察到特定结局或出现低出生体重的时间(孕周)晚于s，则判定对象s为winner，对象t为loser；若二者再次作用效果相当，则判定为tied(图2)。

图2 多个结局变量时组间win-lose判断标准

由此可知，运用Win Ratio法分析两组数据所能得到的结果分为5种：

(1)干预组在评估“子代死亡”水平win(判定干预组win)，频数为Na；

(2)对照组在评估“子代死亡”水平win(判定对照组win)，频数为Nb；

(3)干预组在评估“低出生体重”水平win(判定干预组win)，频数为Nc；

(4)对照组在评估“低出生体重”水平win(判定对照组win)，频数为Nd；

(5)各结局比较均相当(判定为tied)，频数为Ne。

两组间所有可能配对都必须参与比较并得出以上五类结论中的一种，一组获win的同时表示另一组lose，且有Na+Nc=NW，Nb+Nd=NL，Ne=NT。

故采用Win Ratio法分析该项生存资料得两组间所有可能配对数共2726933对，每对随机由一名多微营养组对象与一名叶酸组对象组成，其中多微营养组的赢率(winners所占比例)为8.0%(Na+Nc)，叶酸组的赢率为7.4%(Nb+Nd)，两组相当的比例(tied所占比例)为84.6%，多微营养组比叶酸组的RW值为1.07，95%CI(0.85，1.27)，判断两组间干预效应的差异无统计学意义(表2)。

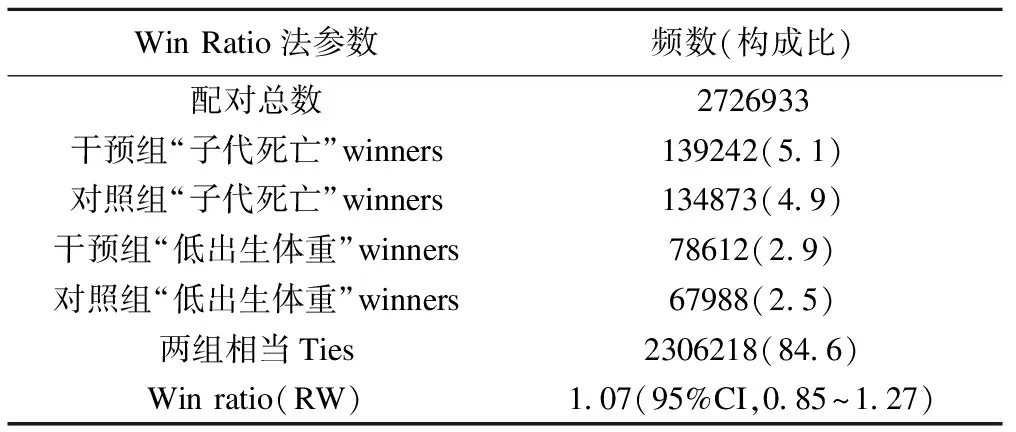
表2 利用Win Ratio法对两组间生存资料进行比较

采用Cox风险回归对两组数据进行生存比较，得风险比为1.04，即对照组的死亡率是干预组的1.04倍，95%CI为(0.83，1.31)，因此认为两组间干预效应的差异无统计学意义(表3)。

表3 利用Cox风险回归模型对两组生存资料进行比较

综上可知，在该实例分析中Win Ratio法所得结论与Cox风险回归一致，均认为两组间干预效应的差异无统计学意义。

讨 论

本文通过一个实例详细阐述了Win Ratio法在对两组间复合终点生存资料进行分析的一些基本理论和方法。在比较两组生存数据时，应用Win Ratio法可在不改变传统生存分析研究结论的基础上考虑生存资料中多种结局的优先顺序，从而解决传统生存分析中因各结局成分不对等而对研究结果产生的影响。

在处理纵向数据时，传统的生存分析方法如Cox回归可用于组间生存资料的比较，计算出P值判断组间差异是否具有统计学意义，并通过计算风险比及其95%CI评价干预效应，但该方法存在两个主要问题。一是Cox风险回归依赖于严格的假定条件，要求必须满足PH假定和对数线性假定，限制了该方法的应用范围；二是在该方法无法区分各结果的主次顺序：当结局具有多个优先级时，Cox风险回归无法区分各结果的主次顺序，从而可能导致试验结果难以解释和/或可存在一定误导性[1-3]。

而现实中常有结局事件由多种结果复合而成的情况，通常在临床和观察研究中很难用单一的结果来描述疗效或暴露情况，疾病或事件的发生往往也难以根据单一的结果作为判定依据。但多种结果的尺度或临床意义可能有差别，结果的不对等性也会对研究结果产生影响。如本文孕妇分娩的不良结局事件包括子代死亡及低出生体重两种成分，但相较于低出生体重，显然子代死亡对孕产妇的影响更大，临床意义更高。在多数情况下，我们很难解释所得复合结局是由哪一成分主导的，倘若临床意义小的成分对结局的驱动作用与临床意义大的成分的驱动作用相反，则会削弱从研究结果中获取可靠结论的能力。若应用Cox回归，则所有结局指标被视为同等意义，无法考虑复合结局中多种结果成分的不对等性对最终研究结论的影响作用。之前有相关研究报道指出，若将多个结局视为单一结局拟合Cox回归模型，或将多个结局分开分别单独拟合Cox回归模型，都将增大回归系数的估计值偏差并降低检验效能[8]。

本研究介绍的Win Ratio法可以很好地解决上述问题。首先，Win Ratio法可通过计算RW值及其95%CI完成对两组生存数据的组间比较并直观地评价组间干预效应，能在得出与传统生存分析方法相一致结果的同时保持与传统生存分析相似的统计能力[15]。同时与生存分析一样，对生存资料中的截尾数据(如失访等未在随访时间内观察到特定结局的情况)亦有具体判定方法。相较于传统生存分析，Win Ratio法不依赖于假定检验，使得该方法有着广泛的应用前景。在此基础上，Win Ratio法另一优势在于关注结局变量各复合成分的相对临床重要性，考虑不平等的复合终点对研究结果的限制影响，以“最劣事件”分析的方式，通过分层分析结局赋予各优先级结局成分数据在数据处理过程中不同的参考权重。本文介绍的是在存在两种结局成分(子代死亡和低出生体重)的纵向数据资料分析中Win Ratio法的应用，而在其他必要情况下，Win Ratio法还可应用于存在更多终点事件成分的时间序列分析中，其基本理论与方法和本文中所介绍一致。

需要指出的是，即便Win Ratio法有上述优点，我们还应注意到该分析方法的局限性。Win Ratio法本身目前尚无公认有效的协变量控制方法，虽然Win Ratio法可以根据分层分析校正分层变量的影响，然而该方法只能控制单一因素的影响，故难以在实际科研工作中校正不同混杂因素对结果的影响，且该方法缺少样本量及样本率估算公式。Win Ratio法的使用范围亦有限制。首先，Win Ratio法难以应用于小样本数据或缺少公认输赢评判策略的数据分析中。与此同时，Win Ratio法不能分析比较纵向数据中不同时间节点的组间效应差异，故限制了其在重复测量设计数据中的应用。

基于以上局限性与不足之处，Win Ratio法只适用于严格控制组间混杂因素的临床试验数据分析中，至于更为广泛的生存资料分析，目前只能作为生存分析的辅助或补充方法。诚然，Win Ratio法的性质和应用还有待进一步探索，亦为广大科研工作者提供了Win Ratio未来发展的研究方向。因国内尚未出现将Win Ratio法应用于生存资料分析的报道，故借此文对应用Win Ratio处理生存资料数据的方法作以介绍，愿更多科研工作者能够了解Win Ratio法并将该方法运用到临床研究的生存资料处理工作中。