基于DMC预测控制算法的智能四驱车控制器设计与仿真

,

(上海应用技术大学 电气与电子工程学院，上海 201418)

0 引言

智能车辆具有参数不确定性、时滞及高度非线性动态特性等特点，是典型的多输入，多输出复杂耦合动力学系统，如何构建可处理其时滞及高度非线性等特性的运动控制方法是实现智能车辆自主行驶的重点和难点[1]。

文献[2]等人提出了横向自适应模糊滑模控制方法，提高了智能车辆横向运动系统的控制精度和响应特性；文献[3]提出基于线性时变预测模型的车辆横向自适应模型预测控制方法，实现了车辆横向车道保持的功能，可有效减低横向位置的偏差和实现较好的车道保持性能。

文献[4-6]提出基于输入-输出反馈线性化方法设计横向控制器的方案，然而，这是一种基于模型的控制方法，这种方法最大的缺陷是它需要精确的对象动力学知识。文献[7-8]根据专家经验提出了模糊横向控制器，但是根据专家经验得到的隶属函数和规则库会产生超调或稳态误差。文献[9-10]提出了一种遗传模糊控制策略，并用遗传算法设计了隶属函数参数和规则库。但是，该算法缺乏模糊控制系统稳定性分析的有效工具。

预测控制最早产生于实际的工业生产过程中，其主要的思想方法是在1978年由Richalet.J等人在1978年提出的[11]。动态矩阵控制(Dynamic Matrix Control-DMC)是一种基于系统阶跃响应的预测控制算法，是目前预测控制理论经常被采用的算法之一[12-14]。DMC 算法具有直接处理纯迟延对象的优点，具备优良的跟踪特性，并且对系统变化有较好的鲁棒特性，在建模困难的工业过程控制中表现出了巨大的生命力。

文献[15]提出了一种基于动态矩阵控制优化的加热炉出口温度的PI-PD控制方法；文献[16]设计了一种基于仿真对象的通用控制开发平台，动态矩阵控制算法在该控制开发平台达到了比较理想的控制效果。但是，由于忽略了扰动等不确定因素的影响，控制对象表达过于简单，因此后期还需要大量的工作来完善平台的设计；文献[17]采用动态矩阵控制算法对燃煤锅炉的蒸汽压力回路进行控制器设计，引入了基于误差的反馈校正策略以克服实际控制中存在的干扰，并基于一阶惯性加滞后模型参数整定方法的研究，实现了参数整定；Chiara Foscoliano等人提出了一种递归神经网络模型，并将动态矩阵控制作为控制生物反应器中含氮化合物的预测控制算法，测试了不同的预测控制器配置，研究了多变量预测控制器在活性污泥法中的应用[18]。

本文结合多变量轮式四驱智能车系统模型，提出了基于DMC预测控制的智能车运动控制算法，完成了智能车系统的控制器设计和相关仿真实验。

基于DMC预测控制的智能车运动控制算法，即保持了预测控制对复杂系统不确定环境的适应性较强，控制效果好、鲁棒性强等优，又结合了DMC 算法优良的跟踪特性，使得控制器对系统变化有较好的鲁棒特性。

对于弱非线性系统，可采用工作点线性化的方法近似成线性系统，进而应用DMC算法；对于不稳定系统，采用的处理方式是先采用PID控制使得系统稳定，然后将DMC算法应用于系统的控制。因此，DMC算法可适用于本文所研究的轮式四驱智能车系统。本文针对智能车运动系统的非线性、多变量、强耦合、参数不确定的等特点，对系统进行线性化处理，并将DMC预测控制算法应用于该系统的控制，其控制结构由预测模型、滚动优化和反馈校正三部分构成。

本文分别基于阶跃响应模型和状态空间模型，使用相关命令函数设计智能车系统的控制器，验证了不同参数对阶跃响应性能的影响，并确定最优参数。同时，使用MPC TOOL工具箱完成智能车控制系统的设计。最后，对3种方法的仿真结果进行了分析和比较，进一步验证了DMC预测控制算法应用于智能车运动控制系统的可行性。

1 系统结构及原理

四轮驱动的智能车是一种非线性、多变量、强耦合、参数不确定的复杂系统，是检验各种控制方法的一个理想装置，受到广大研究人员的重视。为了对其运动进行控制，需要对该智能车系统进行数学建模。

1.1 运动学模型

汽车机器人其运动模型如图1。

图1 四驱汽车运动模型

模型中相关参数及意义如下：L为前后轮间距离；vA(t)为两前轮中心点的速度；vM(t)为两后轮中心M点的速度；δ(t)为前轮转向角；θ(t)为车体航向角；x(t)为后轮中心点M距X轴距离；y(t)为后轮中心点M距Y轴距离。

假设两个轮子有相同的速度v(尽管在实际情况中，转弯时内轮比外轮慢)，一切情况似乎只在位于车轴中心线的两个虚拟轮子上发生。如图2。

图2 四驱汽车简化运动模型

由速度合成规则得：

vM(t)=vA(t)cosδ(t)cosθ(t)

(1)

系统演化的基本方程：

(2)

(3)

(4)

由于前轮加速度和前轮转角的角速度不能无穷大，所以有增补方程：

(5)

(6)

1.2 自然坐标模型

图3 自然坐标系下的四驱汽车简化模型

如图3所示，在汽车的运动过程中，能给予直接控制的有两种：前轮的加速度和方向盘的角度。此处δ表示前轮与汽车中轴线之间的夹角，也就是方向盘的角度；汽车的位置需要3个量来表示：θ为汽车中轴线与水平轴线之间的夹角；汽车的位置(x,y)(汽车后桥中心的位置)；以及汽车方向盘角度θ。

当汽车在未知道路形状时，且没有GPS可以定位时，对汽车的模型进一步研究。此时，没有了定位系统，只能以自身建立坐标系，y失去了意义，x仍然是与边缘的距离，将(1)式代入(3)(4)式,并去掉y(t)，得到：

(7)

(8)

(9)

(10)

1.3 系统数学模型

取状态变量如下：

x1(t)=x(t)，x2(t)=θ(t)，x3(t)=v(t)，x4(t)=δ(t)

输入变量为前轮加速度u1(t)和前轮转角加速度u2(t)。输出变量为后轮中心点M距X轴距离y1(t)=x(t)sinθ(t)，前轮速度y2(t)=v(t)和方向盘角度y3(t)=δ(t)。故得到：

(11)

(12)

(13)

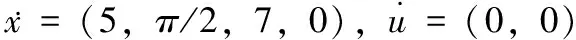
(14)

(15)

2 DMC模型预测控制算法

动态矩阵控制算法是基于被控对象单位阶跃响应模型而建立的一种预测控制算法，设计过程中采用固定格式，控制变量的最优值增量序列由二次型目标函数决定，最优值求解通过改变二次型目标函数中的权系数阵来实现[19]。智能四驱车系统的DMC模型预测控制算法结构如图4所示。

图4 智能车DMC结构示意图

在DMC( Dynamic Matrix Control)算法中，不同时刻控制量的优化通过反馈校正和滚动优化环节实现，以期输出响应逼近期望轨迹[20]。整个智能车动态矩阵控制算法是由预测、控制、校正三部分组成的，该算法结构可用图5加以描述。

(2) 在水力梯度、土体类型一致的情况下，与排水管壁试样直径d=100 mm相比，排水管壁试样直径d=150 mm时单位体积含土量增长了8%～15%，排水管壁试样单位体积含土量随着试样面积的增大而增大。

图5 SISO动态矩阵控制算法结构图

本文假设阶跃响应控制时域长度为M，预测时域长度为P，根据频率分辨率取时域截断长度为N。基于阶跃响应的预测模型为式(15)：

i=1,2,…m,j=1,2,…n

(16)

(17)

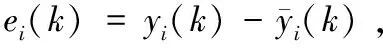
Ypi(k+1)=(ypi(k+1),ypi(k+2),…,ypi(k+P))T=

i=1,2,…m

(18)

将ΔUj(k)化成全量形式，得到式(18)：

(19)

令：Rij=GijS,γij=Gijα

则式(18)变为：

(20)

设第i个过程的P步参数输出为式(20)：

Yri(k+1)=(yri(k+1),yri(k+2),…,yri(k+P))T

(21)

为了实现对参考轨迹的跟踪，应满足式(21)：

(22)

为使上式性能指标线性化，将式(21)改写成式(22)：

(23)

结合式(21)和式(22)可得：

(24)

对控制施加幅值约束，不失一般性，假设控制幅值的下限为零，即：

0≤Uj(k)≤ujmaxβ,j=1,2,…,n

(25)

其中：ujmax为第j个控制的最大幅值，β=(1,1,…,1)T,0=(0,0,…,0)T。如果控制幅值的下限约束为负，则可通过坐标或利用线性规划变量非负化的方法使其为零，以满足单纯形法迭代寻优的要求[11]。对式(24)引入相应维数的正、负偏差变量列向量，使不希望偏差最小化，则式(24)可变为：

(26)

动态矩阵控制算法流程图如图6所示。

图6 动态矩阵控制算法流程图

3 系统控制器设计

3.1 基于阶跃响应模型的控制器设计

本章选择由第2章建立的四驱智能车数学模型，利用MPC TOOL BOX命令函数对控制器进行设计。MATLAB提供了MPC状态空间模型的预测控制器设计功能对动态矩阵控制方法的支持，有关的函数能够基于阶跃响应模型的模型预测控制器设计与仿真。

针对四驱智能车系统，本文设计了输入/输出无约束的MPC控制器。在利用动态矩阵控制算法设计控制系统的时候，本课题通过对代码中参数试凑并结合工具箱及Simulink仿真的方法来确定DMC算法的参数值。

3.2 基于MPCTOOL界面的控制器设计

MATLAB的MPC工具箱具有强大的设计和分析功能，能够对预测控制中涉及的多种算法进行仿真验证。为了实现对四驱智能车系统的动态矩阵控制，完成通过命令函数实现MPC控制器设计之后，本文利用MPC模型预测控制工具箱对智能车系统进行控制器设计。

首先，建立智能车系统模型，确立状态空间表达式，并将sys函数导入MPC工具箱。基于MPC控制器的智能车系统SIMULINK模型如图7。

图7 基于MPC控制器的四驱动智能车系统控制仿真图

控制器参数模型设置为采样时间为0.1，预测时域为6，控制时域为2。无约束条件，输入加权矩阵权值分别为0.1,0.05。输出误差权值分别为0.95，1，1。设定点的信号类型为阶跃信号。

3.3 基于状态空间模型的控制器设计

在MATLAB模型预测控制工具箱中，提供了MPC状态空间模型的预测控制器设计功能。针对四驱智能车系统，本文设计了输入/输出无约束的状态空间模型预测控制器。取二次型性能指标的输出误差加权矩阵ywt；uwt为二次型性能指标的控制量加权矩阵；M为控制时域长度；P为预测时域长度；tend为仿真的结束时间；r为输入设定值或参考轨迹；无约束条件下，ulim=[]， ylim=[]；kest为估计器的增益矩阵；z为测量噪声；v为测量扰动；w为输出未测量扰动；wu为施加到控制输入的未测量扰动；y为系统响应；u为控制变量；ym为模型预测输出。

4 实验结果与分析

4.1 基于阶跃响应模型的控制器仿真分析

输出误差加权矩阵取[0.95 1 1]，控制量加权矩阵取[0.1 0.05]，预测时域P取6，仿真时间为4 s，采样时间为0.1 s，控制时域M取2。仿真结果如图8。

图8 基于阶跃响应模型的MPC控制器阶跃响应曲线

调试过程中，本论文对影响阶跃响应曲线的几个参数值进行了调试，并对仿真结果进行分析。仿真过程中，根据香农定理，采样时间T=0.1 s。由于系统不存在时滞，所以不必考虑对象的时滞。为了保证系统的稳定性，选择预测时域和输出加权矩阵的时候需满足一定的条件。

(1)为了进一步分析预测时域对控制性能的影响，本论文分别对P=6,10,20,30的情况进行了仿真，仿真结果如图9和图10。

图9 预测时域P参数影响仿真第一组结果

图10 预测时域P仿真第二组结果

由仿真图9和图10可知，预测时域P的大小对过程的稳定性和快速性有很大影响：P的取值越大，系统越稳定，但是其快速性将会越来越差。P取6时，系统在2 s内达到稳定，随着P的增加，系统达到稳态时间不断增加，取30的时候，系统快速性较差。实际调试过程中发现，虽然理论上P足够小，即P=1时，可以实现最优控制，但是这种选择方式要求预测模型要足够准确。本论文选择的是经过线性化处理的智能车模型，若预测时域取得较小，系统会出现模型失配的现象，尤其是加入噪声干扰后，系统的鲁棒性非常差。调试发现，预测时域取值过大时，虽然能保证系统的稳定性，但是其动态响应会非常缓慢。因此根据智能车伺服对象的快速性和稳定性的要求，本论文通过调试，选择预测时域值为6。

(2) 为了进一步分析控制时域对控制性能的影响，本论文分别对控制时域M=2,5,10,20的情况进行了仿真，仿真结果如图11和图12。

图11 控制时域M仿真第一组结果

图12 控制时域M仿真第二组结果

控制时域长度M在优化性能指标中表示所要确定的未来控制量的改变数目，即优化变量的个数。由仿真图11和图12可见，在预测时域长度P已知的情况下，控制时域长度M越小，各采样点的输出值跟踪期望输出的性能越差。M=2时，阶跃响应的超调虽然小于M=5时，但系统的响应速度较后者明显减慢。可见，对快速性要求不高的系统，控制时域取较小值，容易得到稳定的控制和较好的鲁棒性。同时，随着控制时域长度M的增大，系统的动态响应不断改善，系统的灵活胜和快速性增加，但是系统的稳定性和鲁棒性会变差。为了兼顾快速性和稳定性，本论文的控制时域长度取2。

(3)为进一步分析控制量加权矩阵对控制性能的影响，本论文分别对控制量加权矩阵，即程序中的uw矩阵取[0.1 0.05]，[0.1 0.1]，[0.1 0.6]，[0.1 1.5]的情况进行了仿真，仿真结果如图13和图14。

图13 控制量加权矩阵仿真第一组结果

图14 控制量加权矩阵仿真第二组结果

控制量加权矩阵元素通常取相同的值，在调试过程中，不仅要保证系统的稳定性，也要减少控制量输入变化的剧烈程度上。根据控制经验，在实际选择控制量加权矩阵时，令其从零增加。由仿真图13和图14可见，如果控制量价加权矩阵的元素取值过大，例如大于0.6时，系统稳定性被破坏。经调试，本论文控制量加权矩阵取[0.1 0.05]。

(4) 为了进一步分析输出误差加权矩阵对控制性能的影响，本论文分别对输出误差加权矩阵，即程序中的yw矩阵取[0.7 1 1]，[1.1 1 1]，[6 1 1]，[15 1 1]的情况进行了仿真，仿真结果如图15和图16。

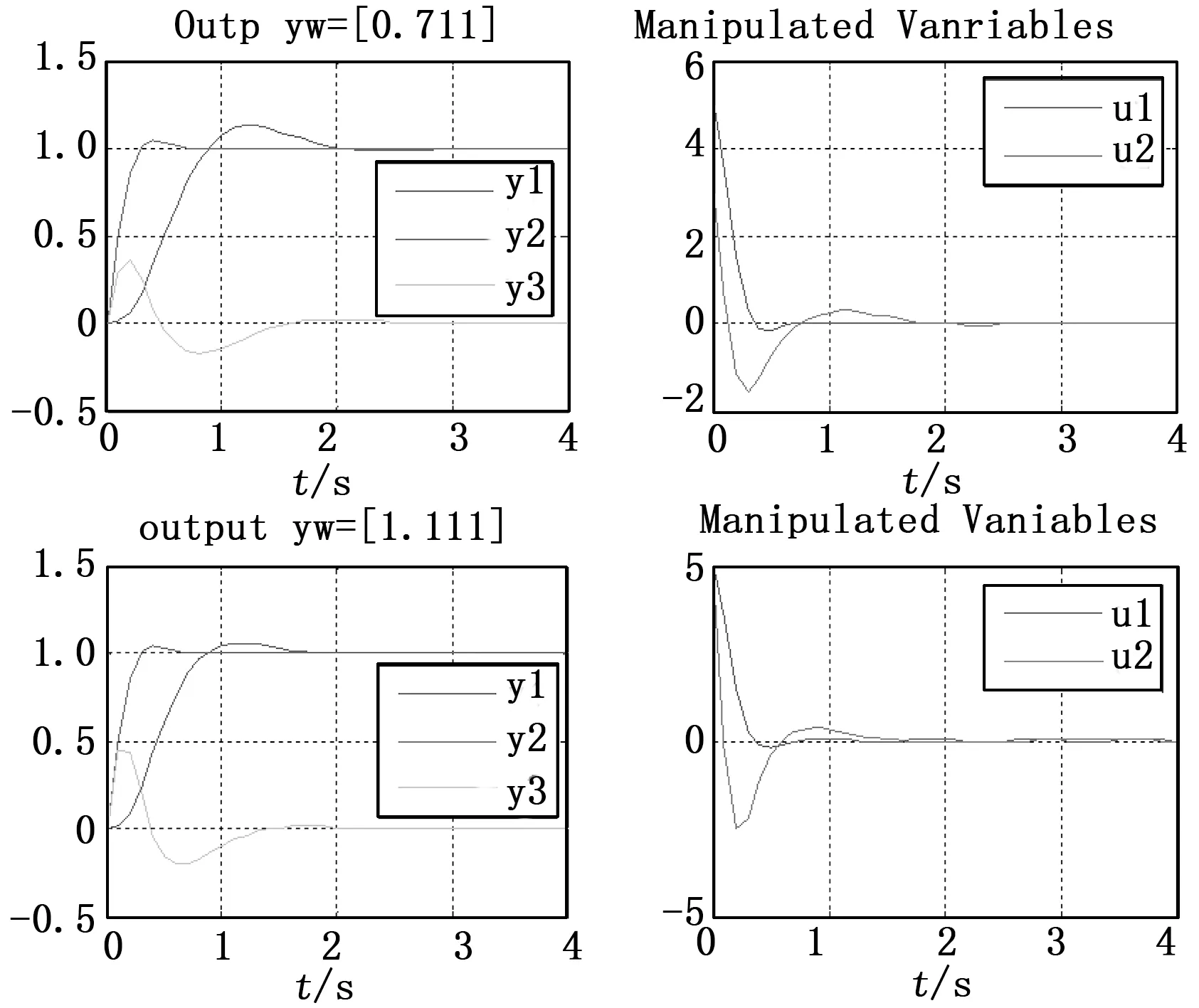
图15 输出误差加权矩阵仿真第一组结果

图16 输出误差加权矩阵仿真第二组结果

由仿真图15和图16可见，输出误差加权矩阵元素较小时，系统的快速性较差。随着元素值增加，系统的超调减小，快速性增加。动态性能得到改善。调试过程发现，如果输出误差过大，会对其他输出变量造成较大影响。经试凑，本论文输出误差加权矩阵取[0.95 1 1]。

4.2 基于MPCTOOL界面的控制器仿真结果

输出变量和输入变量仿真结果如图17和图18。

图17 MPC控制器阶跃响应曲线

图18 MPC控制器输入变量曲线

由仿真结果可见，利用工具箱可以对智能车系统实现MPC控制器设计，达到良好的阶跃响应控制效果。

基于MPC控制器的四驱动智能车系统的阶跃响应仿真结果如图19。

图19 基于MPC控制器的四驱动智能车系统仿真图

4.3 基于状态空间模型的控制器设计仿真结果

仿真结果如图20。

图20 基于MPC状态空间模型控制器设计输出响应和操纵变量曲线

5 结束语

综合比较3种控制器的仿真结果，利用输入输出无约束条件下的状态空间模型预测函数，能够实现四驱动智能车系统的动态矩阵控制器设计。通过对取二次型性能指标的输出误差加权矩阵进行参数调节，可以使系统控制变量变化更平滑，达到比基于阶跃响应模型的预测函数设计更加良好的控制效果。同时，利用工具箱可以对智能车系统实现MPC控制器设计，达到良好的阶跃响应控制效果。由此导出MPC控制器的工作空间，进行下一步SIMULINK模型的搭建。由Simulink仿真波形图可见，利用MPC TOOL工具箱进行控制其设计，可以达到和代码编程设计相同的结果，且可视化效果更好，参数调试更便捷。

有关参数整定的仿真实验结果表明，经过线性化处理的智能车模型，若预测时域取得较小，系统会出现模型失配的现象，尤其是加入噪声干扰后，系统的鲁棒性非常差。预测时域取值过大时，虽然能保证系统的稳定性，但是其动态响应会非常缓慢；随着控制时域长度的增大，系统的动态响应不断改善，系统的灵活胜和快速性增加，但是系统的稳定性和鲁棒性会变差；控制量加权矩阵元素取值过大，会破坏系统稳定性；输出误差加权矩阵元素较小时，系统的快速性较差。随着元素值增加，系统的超调减小，快速性增加，动态性能得到改善，但如果输出误差过大，会对其他输出变量造成较大影响。