融合PCA的支持向量机人脸检测研究
,
(上海工程技术大学 机械与汽车工程学院,上海 201820)
0 引言
人工智能理论在过去的几十年一直在不断发展,但是由于计算机硬件的局限,特别是内存和运算速度的局限,使得很多理论成熟的理论缺少应用。随着计算机软硬件迅速革新换代,人工智能也发展出了很多的应用技术,尤其是模式识别领域的应用,具体包括行人检测、人脸识别、表情识别和语音识别等[1-3]。这些应用的目的是希望设计出像人一样从经验中学习,并做出决策的机器,从而代替人的智慧完成一些特定的工作。而在诸多经验中,人脸表情经验对判断人的心理活动,体察人的喜怒哀乐具有重要意义,如何让机器学习识别人脸表情,是人工智能研究领域的一个热门话题[4]。表情识别研究的对象是包含人脸的图片和视频(视频也是由时间上连续的图片组成),所以如何确定人脸在图片中的位置,成为表情识别的第一步,也即如何实现人脸检测是表情识别的第一步(同时也是关键的一步)。本文就这一问题给出了一种解决方案。
查阅大量文献后,发现目前比较可靠的人脸检测算法主要包括如下四类:
1)基于特征提取和决策树的级联分类器(Adaboost)算法。
2)基于优化理论、泛化理论和核函数理论的支持向量机(Support Vector Machine,SVM)算法。
3)基于贝叶斯先验模型的朴素贝叶斯模型。
4)基于特征提取和权值更新的神经网络算法。
其中神经网络(如BP神经网络、CNN卷积神经网络、RNN循环神经网络等)作为人工智能领域划时代的产物,参考人和动物的细胞感知外物的原理建立起神经网络细胞模型,实现了数据并行运算和网络结构的自适应、自学习,具有训练快速,泛化性良好的优点,但是也有容易陷入局部最优的缺点[5];Adaboost算法采用级联的决策树结构,具有泛化性好,速度快,命中率高的优点,但是需要大量样本提高泛化性,提取的特征值也数量惊人,所以需要消耗大量内存,不适合移植到小型设备[6];而贝叶斯理论需要建立数据的先验概率分布模型,模型建立简单,但是对非典型样本适应性不够好[7];SVM支持向量机算法用到了优化理论、泛化理论和核函数知识,其模型是一个分隔所有数据点的超平面,所有一定有全局最优解,并且因为只需依靠占样本数量少数的支持向量维持超平面位置的特点,不需要大量样本,且泛化性好,缺点是算法设计较复杂,这一点可由序贯最小优化(Sequential Minimal Optimization,SMO)算法来解决[8-11]。
基于对上述各算法优缺点的考虑和本身作者知识的掌握情况,选择SVM支持向量机作为本文所论述的人脸检测算法。
而除了对人脸检测算法本身的选择会影响算法消耗的时间和空间大小,对于数据的保存和使用如果设计的好可也以大大节省算法时间和空间,因此本文还设计了结合奇异值分解(Singular value decomposition,SVD)的主成分分析( Principal Component Analysis,PCA)作为第一环节来实现数据的降维[12]。
在第二环节,降维后的数据经SVM支持向量机训练后保存为分类器数据结构。
到了第三环节,为了减少分类器的负担,提高效率,考虑到肤色在YCbCr颜色空间的分布具有统计学特性,设计了一种肤色高斯概率模型,用以在图片上提取肤色感兴趣域,这样就大大缩小了分类器的筛选范围[13]。
第四环节使用分类器对肤色感兴趣域进行分类,提取出人脸域,这一环节可能提取出多个人脸域,所以设计并查集算法合并同类域,最后得到唯一的人脸域[14]。
1 使用PCA进行样本降维处理
主成分分析( Principal Component Analysis,PCA)是一种分析数据在某空间分布的特征方向,并提取主要方向,用数据在主要方向上的投影来代替它们本身,实现数据降维的技术,可以减少数据所需存储空间。
1.1 使用奇异值分解对样本矩阵进行特征分解
用于训练的样本图片是彩色图片,包括红、绿、蓝(R、G、B)三个通道的数据。灰度图反映的是图片的亮度信息,仅包含灰度(Y)单通道的数据。
本文设定样本矩阵包括个灰度化后的图片样本,每张图片大小都是N=24*24,那么样本矩阵可以表示为:
X=[x1,x2,…,xm]T,M=100
(2)
由于样本矩阵的行和列一般不相等,所以对样本矩阵进行分解需要使用奇异值分解。奇异值分解(singular value decomposition,SVD)作为特征分解在任意矩阵上的推广,可以对任意矩阵进行分解,定义如下:
X=UΣVT
(3)
其中:U和V是酉矩阵,即UUT=I,VVT=I。矩阵U是U空间的M×M阶标准正交基向量矩阵,矩阵V是V空间的N×N阶标准正交基向量矩阵,∑是M×N阶半正定对角矩阵,除主对角元素外其余为0,主对角元素叫做奇异值r=min(M,N),数量为。
由于:
XXT=(U∑VT)(U∑VT)T
(4)
化简为:
XXT=U∑2UT
(5)
所以U矩阵可通过求特征向量得到,同理:
XTX=V∑2VT
(6)
所以V矩阵可通过对XTX求特征向量得到,而∑矩阵可通过对XXT或XTX的特征值开平方根得到。
1.2 PCA主成分分析实现数据降维
PCA主成分分析通过对SVD分解得到的奇异值在主对角线上按大到小排序,舍弃较小的值,剩下的奇异值对应的特征向量也按顺序组成矩阵。设XXT或XTX的特征值为λi,奇异值σi计算公式为:
(7)
且σ1>σ2>…>σr,定义数据压缩率
(8)
σ1,σ2,…σl和对应的特征向量v1,v2,…,vl即样本数据的主成分。η一般取0.6~0.9,η越低表示数据压缩率越低,降维效果越好,同时数据信息丢失的就越多。
变化公式(3),得到:
XV=U∑
(9)
V和∑只保留主成分,于是有:
X[v1,v2,…,vl]=U∑l
(10)
令X'=Xvi(i=1,2,…,L)为X在特征向量vi上的映射矩阵,代替原始数据作为训练数据,维度为M×l(l 支持向量机(Support Vector Machine,SVM)由Broser,Guyon和Vapnik发明。支持向量机的特点是产生分类超平面使数据间隔最大化,使用了核函数,有全局最优解,解具有稀疏性,以及通过泛化误差界来控制样本容量。本文使用一种软间隔SVM向量机,并使用序贯最小算法(Sequential Minimal Optimization,SMO)优化[11]。 对于数据维度为N的样本,可能存在线性不可分的问题,因此也就无法找到可以正确分离两类数据的超平面。于是利用核函数将数据的点积从低维空间映射到高维空间,从而实现高维空间的线性可分,再利用线性可分的原理进行计算。 这里使用高斯径向基核函数: (11) 高斯径向基核函数可以看成一个以xj为中心的概率域,代表xi与xj的相似度,xj即所谓的支持向量,需要通过对目标函数进行优化求解得到。后文的xixj统一用K(xi,xj)或Kij代替。 超平面(The hyperplane)用于分隔两类数据,维度总比数据空间低一维。假如数据线性可分,那么可由许多个超平面按图1分开。 图1 超平面将数据分开 数据点到超平面的位置关系如图2所示。 图2 点到超平面的向量表示 其中: (12) (13) 得到几何间隔和函数间隔的关系: (14) 支持向量机的目的就是最大程度地分开两类数据,所以目标就是最大化数据集中所有点到超平面的几何间隔中的最小间隔,即: (15) 并且有约束条件: (16) (17) Subjecttoyi(wTxi+b)≥1,i=1,2,…,M 为了提高泛化性,允许数据点在一定程度上违反间隔约束,给出松弛变量ξi(ζi≥0,),并设不等式约束函数: gi(w)=1-yi(ωTxi+b)-ξi≤0,i=1,2,…,M (18) 为了将等式约束和不等式约束加入优化目标,设定原问题的拉格朗日函数: (19) 对各个变量求偏导,然后加上约束条件,就是优化问题有最优解的Karushi-Kuhn-Tucker(KKT)条件: (20) (21) (22) (23) (24) gi(w*)≤0 (25) (26) (27) (28) i=1,2,…,M (29) 其中带*的量表示问题的最优解对应的参数值。 式(19)中αi和ri作为拉格朗日乘子同时也表示最优值对约束的灵敏度。C代表安全系数,作用是防止松弛变量对目标函数的影响过大,同时也限制了离群点的αi,即式(26)(称为盒约束,离群点的αi通常很大,需要加以约束,同时也保证了可行域的界,即原问题总有非空可行域)。式(26)由式(21)和式(27)得到。 得到原目标问题和对偶问题的关系: (30) (31) i=1,2,…,M i=1,2,…,M i=1,2,…,M 求出了最优的α*,接着就可以求出最优的ω*、b*、ξ*和r*。 常数 (33) 将式(33)带入式(31)得到: (34) η=K11+K22-2K12 (35) i=1,2 (36) 图3 对变量α2的约束 当y1≠y2时: (37) (38) 当y1=y2时: (39) (40) 由: 可知当K11+K22-2K12>0,W(α2)是下凹函数,更新α2: (41) 当K11+K22-2K12≤0时(当K11+K22-2K12<0时W(α2)是上凸函数,当K11+K22-2K12=0时W(α2)是线性函数),更新α2: (42) 其中: sLL1K12 (43) sHH1K12 (44) (45) (46) (47) (48) 根据支持向量(即α1在0到C之间的向量xi)的性质1=yi(ωTxi+b),得到第一个b的计算公式: (49) 之后的bnew按下式计算: (50) (51) 关于α1和α2的选取采用启发式原则,α1的选择作为外循环,α2的选择作为内循环,一旦外循环选到符合条件的α1,即进入内循环选择符合条件的α2,然后进行优化。 外循环流程: 1)搜索所有样本,选取不满足KKT条件的样本参数αi作为α1。 2)搜索所有参数αi满足0<αi 不断重复1)和2)直到所有αi满足KKT条件内循环流程: 1)搜索所有样本,启发式地寻找使|E1-E2|最大的α2。 2)随机选择参数αi满足0<αi 3)搜索所有样本,选择不满足KKT条件的样本参数αi作为α2。 4)如果找不到合适的α2,就跳出内循环,寻找新的α1。 不断更新一对对α1和α2,并更新ω和b。直到所有样本都满足KKT条件,支持向量机训练完毕。 将M个训练样本经PCA主成分分析压缩后输入支持向量机训练,这里程序代码使用C#语言编写。输出分类器数据结构并保存成文本格式,如图4所示。 图4 SVM数据结构 摄像头采集测试图片的大小统一压缩到300*168。彩色图转化灰度图的公式如下: Y=0.299*R+0.578*G+0.114*B (52) R=G=B=Y (53) 原图经灰度化后由于拍摄时光线不好,图片较暗,灰度值集中在比较小的范围,造成数据稀疏性不够,所以使用光补偿算法扩展灰度值的尺度: (54) (55) (56) 得到光补偿后的灰度图如图5所示。 图5 光补偿灰度图 为了缩小分类器筛选的范围吗,使用肤色高斯模型进行人脸感兴趣域的粗取。由于肤色在YCbCr空间对光照不敏感,所以将RGB空间转化到YCbCr空间,转换公式如下: Y=0.299*R+0.587*G+0.114*B (57) Cb=-0.1678*R-0.3313*G+0.5*B+128 (58) Cr=0.5*R-0.4187*G-0.0813*B+128 (59) 定义Cb和Cr的协方差矩阵为: (60) 其中: (61) (62) (63) (64) 得到肤色高斯模型的计算式: P(Cr,Cb)=exp[-0.5(x-Mean)TC-1(x-Mean)] (65) C=E((x-Mean)(x-Mean)T) (66) x=[Cr,Cb]T (67) Mean=E(x) (68) 采集100个肤色图片样本经过训练后得到肤色高斯模型数据结构并保存为文本,如图6所示。 图6 肤色高斯模型数据结构 对P(Cr,Cb)≥0.6的点灰度值置255,P(Cr,Cb)<0.6对的点灰度值置0得到由肤色概率分割的二值化图片如图7所示。 图7 肤色概率分割二值化图 图8 扫描框扫描过程 使用搜索框扫描图片,搜索框具有cell和size属性,cell代表最小单位边长(像素点数),size代表搜索框边长(cell数)。搜索策略是给size设置初始start值和终止end值。在size从start到end的增长过程中,每当size加1之前,用搜索框扫描一遍图片,搜索策略如下:在移动搜索框之前,将当前框内所有点的P(Cr,Cb)值累加求均值: (69) 如果: (70) 则将该搜索框保存为人脸候选框,保存的内容包括搜索框的长、宽和位置坐标。这里代表肤色概率阈值δ(一般取δ=0.6)。 图9 候选人脸框 使用训练好的SVM分类器对候选人脸框进行筛选,保留输出结果是“人脸”的候选框,最后,定义相似函数将相邻框归为为一个集合,取成员最多的集合求框长、宽和位置坐标的均值,得到唯一人脸框: 图10 合并同类框结果 本文使用的人脸检测算法,在C#平台中对文中所有理论进行程序验证和测试,根据拍摄的300幅测试图片的结果总结如下: 1)使用PCA主成分分析法对样本进行压缩,提高了支持向量机训练速度。 2)支持向量机引入SMO优化算法,实现对非线性数据分隔面参数的快速训练,并使得算法在程序上更容易实现。编译通过的程序根据样本训练得到的分类器数据结构使用文本保存到检测程序根目录,方便检测时调用。 3)使用肤色高斯概率模型粗取人脸感兴趣域,大大缩小分类器筛选范围,提高了检测速度。2 支持向量机原理
2.1 核函数实现数据线性可分
2.2 优化目标的得到






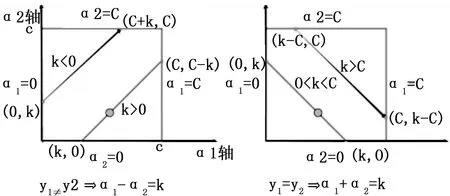
2.3 SMO优化算法

3 人脸检测的实现
3.1 训练支持向量机分类器

3.2 高斯肤色模型粗取人脸感兴趣域






4 结论

