中学数学解题过程中数学方法的应用

江西省吉安市永新县在中中学 谭星明

在中学数学的教育教学过程中，虽然课本中已经包含了大量的优秀的典型例题和习题，并且都配有丰富明了的解题方法步骤，但就目前来讲，数学解题思路和方法仍隐存着大量知识和内涵，鉴于此，在解题过程中对数学方法的揭示与探讨能够有效地提升中学生的逻辑思维和探索创新的能力，加强学生空间想象的能力，将数学的学习能力转化为个体的思维创新力，培养出更多优秀的创新型人才。

一、中学数学的基本内涵

从中学数学的设计特点方面来看，主要是为了提升学生全面发展的能力，同时将数学的学科价值渗透到文化价值当中来。新课程改革的过程中教师更加居于主导地位，学生的主体性得到明显体现。中学数学的解题方式更加符合中学生身心发展、智力水平以及认知结构的特点。中学数学的解题方式符合三维教学目标的基本要求和理念，所应用素材更加关注数学学科发展的实质，而且弹性适中，学生的自主合作、探究能力得到一定的提升。中学数学的教学设计环节包括教学之前的准备工作、课程的开发与设计以及最终的评价与修改工作。数学教材的设计更加体现目标、教学以及评价功能。

二、中学数学解题过程中的解题方式的特点

所谓数学解题方法就是为了达到解决数学问题的目的而采用的各种手段和行为。解题的数学方法经过人们长期的探索和研究已经基本形成了一定的门路，进而形成了较为完备的数学方法。具体来说，数学方法具有三个特征：首先，数学方法的抽象性比较明显，而且多数以简洁性为主。其次，在实际的应用中相对严密，而且具有较强的逻辑性和精确性。另外，在实际的应用过程中易于操作。

数学方法在实际解题中的应用主要是以提供准确地形式化语言、提供分析和计算的方法以及逻辑工具为主。现如今，随着计算机和网络的发展，数学方法的作用日益突出。数学问题的设计一些数学家或者是学者都倾向于借助自身的研究或者是创作精力来设计数学问题，这种数学问题设计的方式不仅具有生活性，而且更加贴近学生的心理，从某种程度上激发了学生的学习兴趣以及积极探索的欲望。对于数学问题中涉及几何以及平面或者是函数等方面的知识，一般都需要学生具有较强的空间思维能力。因此，在实际的解题过程中需要学生多利用图文转化的方式来进行。这种解题方式不仅可以活跃课堂氛围，更能培养学生的思维想象能力，促进学生多方面的发展。

三、中学数学解题的数学方法

1．基本推理方法

所谓推理方法就是根据数学具体问题，按照逻辑学相关理论当中涉及的规则和原则等来进行解题。包括常见的分析法、证明法以及归纳法等。例如，证明在一个三角形当中不能有两个钝角。这类题一般都会采用反证法来进行证明，这就是数学解题的基本推理方法。

2．基本解题方法

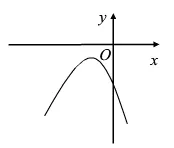
对于中学数学来说，基本的解题方法一般以建模法、代入法、坐标法以及数形结合分析法为主。但是在采用这些解题方法的过程中需要解题人熟练地掌握这些方法和技巧，否则会出现诸多问题。例如，二次函数y=ax2+bx+c的图像如图所示，判定a、b、c之间的关系。这就是典型的数形结合的解题方式。

3．具体的数学解题方法

第一，换元法。我们通常提到换元法，一般应用于某些较为复杂的数学算式当中，将题干中某一部分经过加工改造的某部分用一个新元素代替，使原式简化，方便问题的分析和解决，是数学解题过程中常用的数学技巧。

第二，判别式和韦达定理。在二元一次方程中，判别式Δ=b2-4ac不仅可以判别根的性质，还能够成为一种数学解题的方法，在数学方程组中研究函数性质以及三角几何中都有相当广泛的应用。韦达定理也可以用来讨论根的对称性并求解方程，讨论根的符号，甚至是在二次曲线的问题求解中都有着十分广泛的应用。

第三，因式分解。我们通常所说的因式分解，是将某个多项式分化成几个整式乘积的变换方法，其中等式两边是形变基础。这种解题方法在数学运算中是行之有效地解题方法，在几何、三角和代数中都可以使用。因式分解的方式种类繁多，除教材中例举的提取公因式、分组、公式和十字相乘等方法，还有待定系数分解法、拆项添项法、换元法以及求根分解法等多种因式分解的方法，都适用于解决数学中的问题。

第四，对于函数、方程、不等式，需采用数形结合的思想方法、待定系数法、配方法、联系与转化的思想、图像的平移变换。另外，还有证明角相等、直线平行或垂直、证明线段的比例式或等积式、几何作图等问题，都有具体详细的方法。

数学应用题的教学是如此的重要，教师也要根据学科的特点进行教学，从思想上就要重视起来，使学生能够从内心提高对应用题的重视程度，这是解答应用题的首要基础条件。再者，初中应用题的题型灵活多样，内容广泛，思路也不好把握，因此，初中生要掌握数学应用题的解题方法和技巧也不是一朝一夕的事情，这需要初中生在平时练习的时候要善于积累、加以总结，并在以后的解题过程中进行运用。