“教什么”比“怎么教”更重要——以“解直角三角形”教案打磨为例

☉江苏省苏州工业园区星江学校 张丽华

最近参加学校教研组一次课例（课题是九年级“解直角三角形”）打磨，教师试教之后教学时间不够用，后来经过打磨删减了原稿中很多变式与拓展问题，回归基础，适度变式，从特殊走向一般，使我们对这节课的教学理解走上了新的层次.本文先分别梳理这节课教学设计的第1、2稿，并跟进教学立意的阐释.

一、“解直角三角形”教案打磨

说明：为了便于对比打磨前后的显著区别，分别整理第1稿、第2稿的教学流程.

“第1稿”教学流程

活动1：复习引入

问题1：直角三角形中，除直角外，还有几个元素？

教学预设：学生回答后，教师给出定义：由直角三角形中的已知元素，求出其余未知元素的过程叫作解直角三角形.

问题2：在Rt△ABC中，已知∠C=90°，∠A、∠B、∠C所对的边分别是a、b、c，那么a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？

教学预设：教师与学生互动对话，分类讨论确认以下事实：知道其中的两个元素（至少有一个是边），就可能求出其余三个未知元素.

活动2：例题探究

题型1：已知两边解直三角形.

例1 如图1，在Rt△ABC中，已知∠C=90°，AC=，BC=，解这个直角三角形.

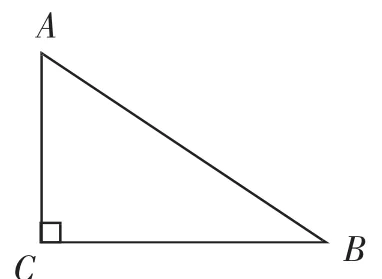
图1

教学预设：先安排学生独立思考，再由学生交流解题思路，最后由教师板书解题过程，示范步骤与格式，强调最后写出“答语”的解题习惯，并继续给出下面一道跟进练习.

练习1：在Rt△ABC中，已知∠B=90°，AC=10，BC=5，解这个直角三角形.

题型2：已知一锐角和一边解直角三角形.

例2 在Rt△ABC中，已知∠C=90°，∠B=45°，AB=12，解这个直角三角形.

教学预设：学生先画出草图分析，确认只有一种可能形状的三角形，然后标注字母识别特殊直角三角形（含45°）并解出这个直三角形，然后给出如下的跟进练习：

教学预设：这道练习没有配图，属于较难题与易错题，学生构图时会有困难，教师不能上来就帮助学生分析，再由学生写过程.可以先安排学生独立练习，诱发错误之后，再跟进究错、订正.

题型3：解非直角三角形.

图2

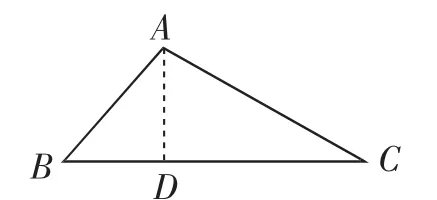
图3

教学预设：由于图形已给定，学生容易想到过点A向BC作垂线段AD（如图3），接着依次在直角三角形ABD、直角三角形ACD中求解.解答之后，给出变式练习.

教学预设：这道题无图，需要分类讨论，学生的主要难点在构图，特别是构造出符合要求的“可能图形”，是很有“高中味”的解三角形习题.

活动3：练习巩固

配了几道练习题，但都没有体现解直角三角形的训练，只是求一个元素，不利于本课目标的达成.

活动4：小结与拓展

先安排几个简单小结问题（如本课学习了什么，感悟了什么数学方法之类），然后给出一道拓展题（先阅读理解，再挑战）：利用45°角的正切，求tan22.5°的值（.限于篇幅，这里不完整再现该题）

试教情况概述：教师组织试教之后，进展到例2就已过去25分钟，到了练习2时，教师就开始加快教学节奏，题目呈现之后学生还没有来得及思考，教师就提前干预，“同学们，看老师来分析一下，你们可能的难点，该这样分类讨论，画出图形，再求解”，然后安排学生计算出相应的结果就推进下一题.尽管这样，不给学生充分的思考时间，讲评到例3后，还是只剩5分钟就下课了，于是对于练习3，更加简要讲授了构图，学生课后再补全过程，然后匆忙小结，后续的练习巩固、小结拓展统统来不及了.这样的试教情况，让执教者感觉非常尴尬，于是经过教研组内充分打磨，形成“第2稿”教学设计.

“第2稿”教学流程

活动1：复习旧知，引出新知

问题1：判定两个直角三角形全等，有哪些方法？

问题2：一个直角三角形除直角外还有5个元素（2个锐角、3条边），除直角外，再给出几个元素就能确定这个直角三角形（形状与大小唯一确定）呢？

教学预设：问题1是引导学生从三角形全等的角度理解直角三角形唯一确定的条件，与问题2互相对应.问题2出示后，先安排学生分组讨论，分类讨论，有序思考，待小组讨论确定至少需要两个元素（至少有一个边）才能确定直角三角形之后，教师摘抄一些计算依据（如两锐角互余的关系、勾股定理、锐角三角函数等）分类整理到黑板上，并给出“解直角三角形”的定义.

活动2：例题示范，同类训练

例1与练习1.（见第1稿中例1、练习1，这里略去）

活动3：例题变式，走向一般

例2 如图4，在△ABC中，∠C=90°，∠B=35°，b=20，解这个直角三角形（结果保留小数点后一位）.

教学预设：这里针对例1进行变式，从特殊直角三角形走向一般直角三角形，这是非常重要的一次修改，因为如果像第1稿中所有直角三角形（包括后续变式问题中的辅助转化之后）都是特殊直角三角形，则引出锐角三角形函数这样的概念就不是“一定必要”的，只有把特殊直角三角形引向一般之后，才能显现出直角三角形“边角关系”（即锐角三角函数）的解题威力.当然，具体求解时，可以安排学生使用计算器参与解答.

练习2：在△ABC中，∠C=90°，a=3，c=5，解这个直角三角形（锐角的角度以度、分形式给出，精确到分即可）.

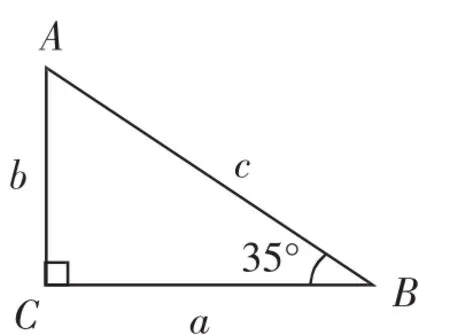
图4

练习3：在Rt△ABC中，已知∠C=90°.已知∠B、c，写出解Rt△ABC的过程.

活动4：师生小结，布置作业

小结问题1：本课学习的解直角三角形与以前所学习的求一些特殊直角三角形某个元素有什么不同？

小结问题2：你觉得解直角三角形的解题步骤中有哪些步骤是值得注意的？

设计3道课后作业，如下：

（1）在Rt△ABC中，已知∠C=90°，c=6，a=3，解这个直角三角形.

（2）在△ABC中，∠C=90°，a=1，b=2，解这个直角三角形（锐角的角度以度、分形式给出，精确到分即可）.

（3）在Rt△ABC中，已知∠C=90°.已知a、c，写出解Rt△ABC的过程.

二、教学立意的进一步阐释

1.想清辨明解直角三角形该“教什么”

对比第1稿、第2稿会发现，我们改动最大的还是教学内容，也就是“教什么”比“怎么教”更重要.“教什么”是基于对教学内容的深刻理解而确定的，以解直角三角形这个知识点为例，它“上承”锐角三角函数的概念而来，又“下启”解直角三角形的应用问题，更重要的是以后高中阶段“解三角形”的基础内容.这样来看，第1稿所选例、习题只是涉及特殊角度的直角三角形显然是不全面的，没有深刻理解教学内容，把解直角三角形只限制在特殊直角三角形的认知“黑屋”之中，不利于引导学生开阔思路和眼光.

2.解直角三角形教学要“从特殊到一般”

根据定义，解直角三角形是已知（除直角外）两个元素（至少一个边）求出其余所有元素的过程.从定义来看，并没有限制所给角度一定要是特殊角度（30°、45°或60°），这也是第1稿教学选题的显著不足.也许有老师会说，很多中考试卷确定只涉及特殊角度的直角三角形求解，这也是现实.因为中考试卷出于考试时间和考试条件（如不允许考生使用计算器）的考虑，往往只安排特殊直角三角形求解，但是作为解直三角形的新授教学，则不能把学生限制在这样的框架之中，而需要从特殊走向一般，这也是“第2稿”安排例2，以及练习2、3的重要意图.

三、写在后面

华东师大李政涛教授提醒教师要加“现场学习力”，而作为教师最重要的“现场”当属“课 堂”（上课或听评课），我们以这次解直角三角形的听课、评课与打磨改进教学设计为例的课例反思也算是发展自己现场学习力的一点努力，欢迎同行的批评，也期待更多同行把更多“课堂现场”中的课例分享，让课例研究丰富多样、精彩纷呈.