在听、评课中发展“现场学习力”
——以“二次根式”起始课听课、评课为例
☉江苏省南京外国语学校 吴凯红
华东师大博士生导师李政涛教授对教师的“现场学习力”有如下论述:良好的现场学习力需要专注其中,即无论是面对自己的课堂、同行课堂或是教研活动,不同的人往往有不同的收获.最近参加一次市级教研活动,观摩学习了一节“二次根式”起始课,不但课上得精彩,而且课后的评课意见也很受教益,现整理出来,并提出自己的一些学习心得,与有兴趣的同行共享.
一、“二次根式”起始课教学整理
教学环节(一) 回顾旧知,引出新知
问题1:4、16、(-4)2、0、2、a的平方根、算术平方根分别是多少?
教学预设:学生回答之后,教师讲授二次根式的描述性定义,形如a≥0)的式子称为二次根式“,”称为二次根号.
接着给出两组练习(略),一组训练如何识别二次根式,追问学生是如何判断的,另一组主要训练被开方式的意义问题.
课堂片段:
师:这节课我们从数的算术平方根说起,4的算术平方根是什么?(等待)
生1:因为2的平方等于4,所以4的算术平方根为2.
其他学生几乎不会,等待了将近1分钟学生还是没有反应.
师:我们一起回顾一下算术平方根吧!我们学习数学就是要表达自己的热情,你们忘了吗?小组一起回顾一下吧!脑子里还没有印象的请举手.
师:16的算术平方根是什么?
师:非常棒!
师:0的算术平方根是什么?
学生继续回答:2的算术平方根是______,a的算术平方根是______.
自主练习:下列式子哪些是二次根式?你是如何判断的?
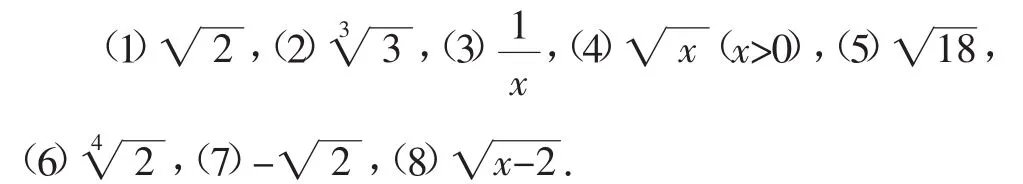
教学环节(二) 从定义出发,探究性质
教学预设:引导学生理解算理,回到定义来说理,即根据乘方与开方运算的互逆关系,可得()2=a(a≥0).
教学预设:引导学生理解算理,回到定义来说理,即根据乘方与开方运算的互逆关系,可得=|a|.如果学生忽略a也可取负值,则安排学生充分讨论,举出不同数来验证、确认.
教学环节(三) 性质运用,化简计算
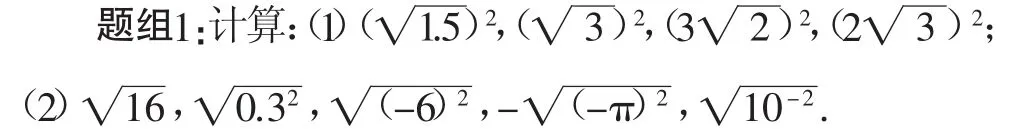
题组2:下列二次根式有意义时,分析x的取值范围.
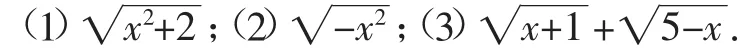
教学环节(四) 反思小结,完善板书
小结问题:同学们是如何理解二次根式的定义的?
在本课中是如何得到二次根式的性质的?
完善板书如下:

二、评课意见摘选
评课老师1:这节课从温故知新开始,充分等待学生,抓知识的生长点——算术平方根,体现了客从何处来的理性追问精神;回归定义,善于捕捉课堂生成,紧抓新知生长点;关于二次根式性质探究,紧扣代数学习的套路,从定义到性质再到运算,整个过程顺畅、自然;对于本课重、难点,在课堂小结时做得细致到位,而且有一个漂亮的板书.可以说,这节课不仅让学生学习到了二次根式的相关知识,还让学生积累了从特殊到一般和从抽象到具体的数学思想.
评课老师2:在不断的追问中体现教师的主导性,又体现着学生的主体性;在自主练习中凸显相关的性质;在小结概括中知二次根式全貌,能让学生知其然并知其所以然,自始至终强调学生怎么想的.在课堂小结时,不落俗套.教师设计了两个问题:你是如何理解二次根式的定义的?如何得到二次根式的性质的?通过二次根式概念和性质的学习,你积累了哪些学习方法和经验?关于本节课上小组活动的处理方式,有猜想时看似教师完全放手,让学生学会学习,让学生归纳总结,又没有完全放手,在小组合作的部分给出了要求,放和收做得自如.关于定义,有一个疑惑,提出来与大家一起思考:根据定义,形如(a≥0)的式子称为二次根式,那么根据定义,3是不是二次根式?-是不是二次根式?
评课老师3:这节课中,教师对二次根式有深刻的理解,从带根号的算术平方根出发,从特殊值代入并探讨到总结一般性的规律,通过算术平方根定义验证,注重知识课堂的生长.教师给学生充分留白,静静地等待学生的回答,对于性质的处理,学生的回答不对,教师一个小问题的引导,利用()2=4,()2=a,提问学生是否还有其他方法来验证.探讨性质时,一步步引导学生验证方法,走套路.对于性质3的证明,充分利用李庾南老师倡导的自学·议论·引导,现学现卖.对于2个性质异同的理解(与()2),从学生对于性质的把握看应该掌握了.
评课老师4:概括起来,用以下几个关键词来评这节课,就是展示多、结构佳、思维深、创意好.具体来说:
(1)展示多.执教老师在课堂上让学生说,说结果,在白板上写出来到前面展示.充分将思维误区展示,让学生自己发现错误并纠正,教学过程中注重抓取学生错误,是化错教学.
(2)结构佳.板书非常棒,体现了结构化板书的特点.
(3)思维深.开课由定义出发,从算术平方根走向二次根式,在课堂上渗透了从具体到抽象、从特殊到一般的数学思想方法.很好地培养了学生的思维能力,通过不断追问,让学生联想到原生态的算术平方根的意义,通过追问,让学生的知识点得到生长.
(4)创意好.体现“学材再建构”,重组了教材,凸显了常见的数学思想方法:类比、从特殊到一般的数学思想方法.
三、进一步的思考
1.深刻理解教学内容,从定义出发
课堂教学要求应“标”而定,即对照课标,学习知识开始时要简单,如中国古代山水画卷一样渐次展开.二次根式的知识生长点在算术平方根,所以选择从算术平方根出发定义二次根式并依据定义探究归纳二次根式的性质,这个过程看似慢、低效,实质上是向学生渗透“回到定义”去研究的学习方法.事实上,不只是新知探究要坚持“从定义出发”,解题教学更需要向学生传递“回到定义”的解题思想.比如,上文评课老师2提出的问题是不是二次根式?-是不是二次根式”,我们仍然应该回到定义来思考这个疑惑.二次根式的定义是“形如(a≥0)的式子称为二次根式”,根据定义一定是二次根式,但是3是一个二次根与3的积,在辨析二次根式时应该回避这类问题,教师本人不应该纠结,若纠结说明教师对描述性定义 没有达到深刻理解.
2.内容简单的课如何“教活”“教深”
有人说,“二次根式”起始课内容简单,没有什么好讲的,二次根式的性质也是显而易见的,没有什么好讲的,上面的课例是不是内容太少、容量不够?这是当前很多习题单式导学案的通病.教师对概念教学的认识不够,往往对内容简单的课通过加大题量来应对教学时间,这是得不偿失的.我们认为,对于二次根式的性质,不能简单“一带而过”,而应该与学生一起讨论、举例验证,作必要的推理演算,即从特殊数入手到一般推导再证明.在上面的课例中,至少体现了两种数学思想方法,即向学生渗透从特殊到一般、从具体到抽象的数学思想方法.

