重视练习梯度设计,提升巩固训练效度*
——以“整式乘法(第1课时)”教学为例
☉江苏省盐城亭湖新区实验学校 王国强
巩固训练是课堂教学的重要组成部分,其担负着固化新知、建构网络的重任.因而,巩固训练题的设计也应是大有讲究的,我们应随着学生对知识认知的不断加深,而呈现难度递增的配套练习以及时巩固新知,提升学生的应用能力.然而,在近期的一节随堂课观摩中,教者所设计的练习只有深度,没有梯度,让学生解答交流的热度降低,课堂应有的温度下降,教学效果并不理想.现呈现这节课的部分练习,并谈一些个人看法,不妥之处,敬请批评指正.
一、“整式乘法(第1课时)”的练习设计及简析
1.新知获得后的即时巩固
背景:教师根据预设情境,引导学生抽象出“单项式乘单项式”的运算法则,需要一定的练习对刚刚获得的法则进行巩固.
练习设计:
辨一辨:
(1)4a2·2a4=8a8. ( )
(2)6a3·5a2=11a5. ( )
(3)(-7a)·(-3a3)=-21a4. ( )
(4)3a2b·4a3=12a5. ( )
教学过程简述:教师逐题投影,让学生判断对错并交流错因、矫正结果.由于刚学法则,学生对四题的对错并不是十分清楚,在交流时,很多时候是老师与少数优生间的对话,大多数学生保持了沉默.
简析:在法则归纳后,对其进行即时巩固,这是很正常的.但由于这里是运算法则,而非基本概念,以“辨析”的形式巩固,是对法则的逆向应用,既需要算,又需要进行比对,在判断出对与错后,教师还提出了修正结果的要求,这样的巩固,没能顺应学生认知发展的方向,原来抽象概念时的“热乎劲”,被迎面而来的“质询”迅速降温,教学效果自然就不够理想了,因而,笔者建议将上述练习调整为基础计算.
2.例题教学后的范式仿写
练习设计:
算一算:
(1)xn+1·2x;
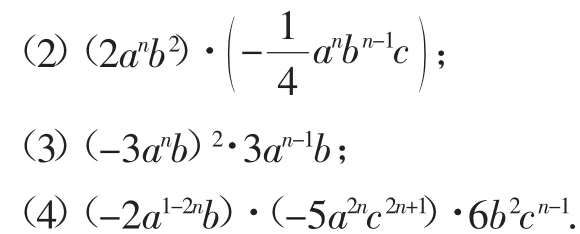
教学过程简述:在教学例题“(1)(-5a2bx)(-3a);(2)(2x)3·(-5xy2)”完毕后,教师投影“算一算”,让学生自主解答,在巡视中发现部分学生做到第(3)题时,教师安排4名学生板演.8分钟后,组织交流,板演的4名学生中,(1)(2)均正确,(3)(4)出错,教师请其他同学帮助分析出错原因,并进行纠正,由于教师在例题(2)教学时未明晰运算中先算乘方,导致很多学生都无视了题(3)中-3anb括号外的2次方,经3分钟的讲评纠正,错误被清除.纵观全班学生解答情况,发现班级中绝大多数学生对这种指数中含字母的运算很不适应,出错率极高,看来这样的练习设置与学生的认知需要及知识的发展方向偏离,如果再教,必须进行适当调整.
简析:按理说,给出了两道例题的解答过程,教师的分析交流到位了,模仿解答几道配套练习是不会出现上面这样的状况的,然而由于教师人为加大了运算背景的深度,让指数由数变为了字母,这对尚未学习整数指数幂运算的学生来说,确实难度不小.如此设置,偏离了教学方向,不仅没能起到“巩固法则,应用范式”的作用,反而让学生感到“这个运算好难”,使得原本就存在的对整式运算的畏难情绪进一步蔓延.如此教学,必然会导致运算能力下降,学习信心下降,因而建议调整此类例题后的范式训练,采用贴近例题、难度相当的变式训练,来达成应有的效果.
3.总结提升后的强化训练
练习设计:
练一练:
(1)若n为正整数,且x3n=2,求2x2n·x4n+x4n·x5n的值;
(2)若(x2y3)m·(2xyn+1)2=x4y9,求m、n的值.
教学过程简述:在本节课的小结归纳后,教师给出了上述练习,让学生自主解答,虽然也给出了近10分钟的时间,但很少有学生能够给出正确的结果和规范过程.最终,教师通过讲解给出了正确的过程和结果.在这种情况下,仍然有很多学生无法理解教师给出的解题过程.
简析:从教学效果看,这两道题所进行的强化训练是失败的.暂不讨论例题的指向,仅从教学所用的时耗与学生的反应看,教学效果是不好的.就算教师再花些时间,也无法让学生深入理解这两道题的真正内涵.细细分析,这两题既有字母指数参与了运算,又有方程的渗入和等量代换思想的应用,知识层面上的需求已远非本节课所学能够解决的,加之学生的转化能力不强,想要他们给出规范的过程实在不易.笔者认为,作为一节新授课,虽然有很多运算、方程的知识作铺垫,但是过高的知识要求已经让这两题的教学偏离了本课时的教学目标.这样的练习设计考验着学生的意志力,不少学生会因为“看着就不会”而失去学习的信心.因而,对这样的练习进行调整是必要的,而且是极为迫切的.
二、练习的优化设计及意图分析
1.新知获得后的即时巩固
题组1:
计算:
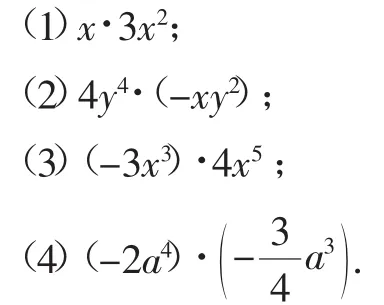
设计意图:这些题目都是非常简单的,不用动笔,口算就可以给出结果.对于刚刚获得乘法运算法则的学生,用这样的练习进行训练,无疑是最适宜的.这样的运算,只需要将法则的简要陈述与具体运算情境(题目)结合起来便可达成结果的“输出”,即时巩固将顺利达成.
2.例题教学后的范式仿写
题组2:
计算:
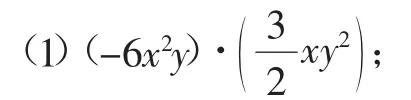
(2)(-2ab2c)·(3ac2);
(3)4x2y·(-3xy2)3;
(4)(-2x2y3)2·(xy)3.
设计意图:四道计算题紧扣例题的形式,得出与例题几乎一致的两式相乘的格式.(1)(2)是对例题(1)的复制,(3)(4)是对例题(2)运算过程的应用,四题无论是过程,还是结果,都指向了“范式仿写”这一目标.这样的练习设计,强化了学生对例题仿写过程的深度感知,确保学生能学到正确的知识与训练有效的技能.
3.总结提升后的强化训练
题组3:
(1)下列各式中,运算正确的是( ).
A.3a3·2a2=6a6B.2x2·3x2=6x4
C.3x2-4x2=12x2D.5y3·3y5=15y15
(2)计算:
①(-5a2b3)·(4b2c2)2;
②(-ab)·(-2a)3·(-3ab)2.
(3)一长方体的长、宽、高分别为(2x)3、(3x)2和2x,求它的体积.
设计意图:承载“单项式乘单项式”运算的载体是多样的.本节课的教学,不可能只是“纯式子”的计算情境,还应有更丰富的生活情境和多样的题型情境.从形式上看,笔者设计的这组题,无论是题型情境,还是项目的情境,都是多样的.再者,与题组1、2相比,题目的难度明显增加,虽然没有优化前的练习难,但就这三题而言,对学生提出的应有的思维深度和宽度的要求还是与教学目标紧密契合的.笔者认为,进入到总结提升环节后,我们应该拓宽学生思维的深度,做点与本节课内容相关的有适当难度的题目,但设计时一定要把握好这个“度”.
三、几点感悟
1.练习设计的目标一定要明确
既然是巩固训练,自然应突出“巩固”,这就是练习设计的目标,在为一节课设计巩固练习时,既要关注练习的作用,也要关注练习的价值,而两者相比,目标是第一位的,没有准确的目标,再好的练习对于课时教学来说也是不适用的.具体来说,练习设计应关注环节目标(即课堂中某一时段的教学目标)和课时目标.课时目标和环节目标都很小,但要想把握准确实不易.我们在设计练习时,对课时目标的关注度是很高的,对环节目标的关注度却不高,尤其是我们往往会忽略或淡化教学练习环节对目标达成的作用考量.说实话,本文中没有优化前的练习,与整个单元目标是匹配的,而“辨一辨”与课时目标是完全一致的,但这一练习放在学生刚获得新知识后,是十分不妥的,这与环节目标“巩固刚刚获得的乘法法则”是不匹配的.因而,笔者对其作出了优化,改为简单的“口算题”,为的就是即学即用,以环节目标的达成助推课时目标的实现.
2.练习设计的层次一定要清晰
课堂教学不能如穿衣服那样可以“混搭”,尤其是练习的设计,一定要遵循“循序渐进,螺旋上升”的原则.作为新授课,练习的层次感要强,呈现的练习应具有清晰的梯度.笔者认为,该难的时候一定要难,该容易的时候就要容易.难题、易题的“混搭”,必将打乱常规教学秩序,任何一次思维的停顿都将会成为干扰教学推进的障碍.此外,难易题的无序训练不能出现在新授课上的原因还有两个:一是,学生的思维会随着难易交替波浪翻滚,不利于思维和结构的优化与思维层次的明晰;二是,难易的交替展示,不利于突出课时教学重点,让学生探究的精力平均耗费在各个时段上,什么地方重要,什么地方不重要,注意力不够集中的学生是无法体会到的.事实上,本文中未优化的练习,自始至终都被加在一个超越本课时目标的高度上,虽然有一定的层次感,但其起点与终点间的间隔并不明显,也就让知识基础薄弱的那些学生从一开始就无法“入格定位”,找到属于自己的解题路径,接下来的问题解决必然是无法实现的.
3.练习设计的源头一定要准确
在笔者听的这节随堂课中,随着执教者教学进程的推进,笔者始终有一个疑惑:“他是从哪儿弄到这些练习的?”课后,在与执教者交流时了解到,这些例题来自于从网络上下载的课件及与之配套的导学案中,教者并未进行任何调整和修改.笔者认为,这种做法是十分不妥的.练习设计,务求清本正源,设计的根基应是教材,呈现的练习可以略微高于教材,但绝不可偏离教材.看看上面的练习设计及简析中展示的这些练习,与教材配套练习相差甚远.笔者翻看了课本,几乎很少见到字母指数的乘除运算,至少在苏科版初中教材中是这样的,而在笔者听的这节课中,这样的运算却反复出现,对教材的背离让教学效果不明显是必然的.再看看笔者所进行的优化,所有的练习都紧扣教材,甚至有些题目就是教材原题或改编题,将这样的练习适时呈现,效果肯定不会差到哪儿去.这就给了笔者一个启示,教材的工具性对教学内容的体现,不应只停留在新的知识与技能上,还应包括用以巩固这些“新知新技”的配套练习.我们应用好教材,在教材中找到练习的源头活水,从而达成配套训练效应的最大化.
4.练习设计的变式一定要多元
一题多变、一题多解、一题多用,是培养学生思维能力,提升学科素养的重要方法.通过练习的变式训练,有助于学生在变中求知、变中思维、变中延展.当前,正值我市“让学引思”课堂教学改革进入纵深阶段,为践行“让学引思”,将课堂主动权彻底还给学生,充分体现学生的主体地位,做到“真让会引,善学真思”,实现高效课堂、有效教学.笔者通过多次听课、研讨、实践,同时积极参与我校课改实践“基于微型课基础上的集体备课”,从备微课、备教材、备学生、备练习入手,针对练习设计的变式要求,多元化、广视角、全方位地进行研究与创新,努力探寻变式练习的新方法:图形可变、数据可变、条件可变、结论可变、难易可变.从而激发学生的学习兴趣和探究热情,引发学生去探索、去思考、去创新,诱发学生思维的再发散、再联想、再拓展.从“变”的神奇中吸引学生爱数学、学数学、做数学,进而实现练习设计“由点到线——由线到面——由面到体”的多元化变式,培养学生求异、发散、整合等创造性思维能力,最终实现将练习设计由“情境化”向“生活化”转变,贴近实际、贴近生活、贴近活动,让学生通过数学学会思维,在练习的变式中深化思维、拓宽思路、创新求异,力求变出新知、变出新意、变出新法.

