错误也是“财富”

☉山东省莱芜市雪野中心中学 毕于茂

作为教师，都希望学生学习内容一听就会，作业一做就对.然而，现实并非如此.在日常教学中，学生数学作业中经常会出现这样或那样的错误，其实这也正常，不经风雨，怎见得彩虹，这正是学生认知规律的体现.正如当代科学家、哲学家波普尔所云：“错误中往往孕育着比正确更丰富的发现和创造因素.”那么，教师如何善待这些错误，将错误变废为宝，让错误成为“财富”？笔者结合初中数学教学实践，谈几点做法与体会.

一、“误”中有悟诚可贵

在数学教学中，作为教师，不能轻易放过学生的任何一个错误，没有错误就没有成功.让学生自己发现错误，自己纠正错误，这才是学生纠错的最高境界.教师可以将学生的错解公布出来，作为第二次作业布置给学生，让学生来一次纠错大行动，这不仅符合初中生的年龄特点和认知水平，更能引发学生浓厚的兴趣.

例如，在学习全等三角形时，笔者给学生布置了两道全等三角形的判定与性质的证明题，收上来批阅的时候，发现学生的解题过程“大病没有，小病不少”，为此，笔者张榜了两个具有代表性的错解，要求学生来个“捉错大行动”

第1题：已知：如图1，AC⊥BC，DC⊥EC，AC=BC，DC=EC，求证：∠D=∠E.

下面是小A同学的方法：

证明：在△ACE与△CBD中，AC⊥BC，DC⊥EC，则∠ACB=∠ECD=90°. 又AC=BC，DC=EC，则△ACE≌△BCD，则∠D=∠E.

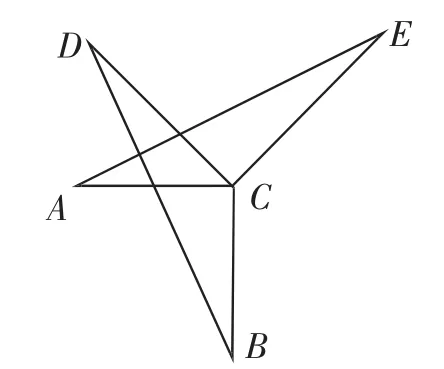
图1

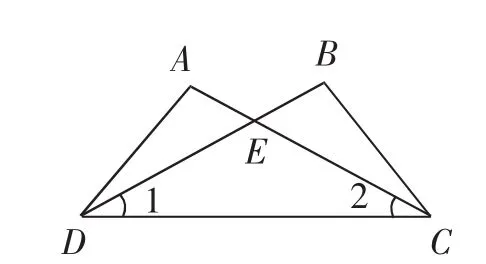
图2

第2题：如图2，已知AC、BD交于点E，∠A=∠B，∠1=∠2.求证：AE=BE.

下面是小B同学的方法：

证明：在△ADC和△BCD 中，∠A=∠B，DC=DC，∠2=∠1，则△ADC≌△BCD.

则△ADC-△DEC=△BCD-△DEC，即△ADE≌△BCE.

则AE=BE.

错解张榜公布后，学生议论纷纷，跃跃欲试，都想做一回“捉错英雄”，可有些学生就是找不出其中的错误.而班内堪称“解题王”的王俊生同学，勇敢地揭下了榜，并且公布了自己的“战果”.下面就是王俊生同学的纠错战果.

第1题：小A的证明似乎有理有据，但细心的你是否发现，上面的证明中，错误地应用了“SAS”，即∠ACB与∠ECD并不是这一对三角形中的内角，因此他用的是“歪理”.

正确证明：由AC⊥BC，DC⊥EC，得∠ACB=∠ECD=90°.则∠ACE=∠BCD.

在△ACE与△BCD中，AC=BC，∠ACE=∠BCD，DC=EC，则△ACE≌△BCD，则∠D=∠E.

感悟：全等三角形的判定定理是“法律”，证明三角形全等必须“遵纪守法”.

第2题：小A的证明中，将等式性质盲目地搬到了全等三角形中，这是完全错误的.

正确证明：在△ADC和△BCD中，∠A=∠B，DC=DC，∠2=∠1，则△ADC≌△BCD.则AD=BC.

在△ADE和△BCE中，AD=BC，∠A=∠B，∠AED=∠BEC，则△ADE≌△BCE.则AE=BE.

感悟：代数和几何虽然有联系，但它们之间也存在着很大的区别，我们不可不分青红皂白而张冠李戴.

这种纠错行动很特别，很有趣且很有效.从纠错中引发学生的学习兴趣，这远比学生纠错有意义得多.因此，善待学生的“错误”，如何把“错误”变成教学资源，是一个值得研究的问题.从中我们不难得到：错误取之于学生，又用之于学生，这样组织学生改错，往往会产生更好的纠错效率，更能使学生有效地避免“重蹈覆辙”.

二、无中生“误”情有原

常言道：防患于未然.又云：亡羊补牢，未为晚矣.意思是说，在问题没有发生的时候，要有防范意识，即使发生了，只要以后多加注意，也没有什么问题.其实，学生学习数学不就是如此吗？作为教师，不鼓励学生犯错，应给学生防范错误支招.当学习了某个单元的知识后，教师可以让学生自己去发现错解，搜集错解，找到错误的原因.

例如，在学习了因式分解后，我发动学生开展搜集因式分解的错解行动，并要求给出正确解法，部分成果如下：

1.符号出错

例1 分解因式：-ab（a-b）2+a（b-a）2-ac（a-b）2.

错解：原式=a（a-b）2（-b+1-c）.

正解：原式=-a（a-b）2（b+c-1）.

2.公式用错

例2 分解因式：4（2p+3q）2-（3p-q）2.

错 解 ：原式=［4（2p+3q）＋（3p-q）］［4（2p+3q）-（3pq）］=11（p+q）（5p+13q）.

正解：原式=［2（2p+3q）］2-（3p-q）2=（4p+6q+3p-q）·（4p+6q-3p+q）=（7p+5q）（p+7q）.

3.分解不彻底

例3 分解因式：8a-4a2-4.

错解：原式=4（2a-2a2-1）.

正解：原式=-4（a2-2a+1）=-4（a-1）2.

4.盲目展开

例4 分解因式：（m+n）4-18（m+n）2+81.

错解：原式=［（m+n）2-9］2=（m2+2mn+n2-9）2.

正解：原式=［（m+n）2-9］2=［（m+n+3）（m+n-3）］2.

从学生搜集的错解可以看出，错解已成为一种“反面教材”，学生理解了出现错解的原因，也就真正掌握了因式分解的内涵.这样的搜集错误活动，有助于学生养成数学反思的好习惯，用批判的眼光看待错解，更有利于学生数学学科核心素养的形成.

三、执“误”探究价更高

爱迪生发明了电灯，经历了无数次失败，但他没有停止试验，依然默默探究.面对学生的错误，教师也应该引导学生像爱迪生那样不畏艰难，从失败走向成功，从数学学习的过程中，培养学生坚韧不拔的学习品质.

例如，有一次，笔者布置了这样一道题：已知方程x2-mx+1=0的两个实数根分别为x1、x2，求的最大值.

批阅作业的时候，笔者发现班级里八成的学生都是这样解的：

解：因为方程x2-mx+1=0的两个根分别为x1、x2，所以，由根与系数的关系有x1+x2=m，x1x2=1，所以（x1+x2）2-2x1x2=m2-2≥-2，所以的最小值是-2.

第二天上课，笔者提出疑问：两个实数的平方和怎么是负数呢？学生面面相觑.

笔者追问：题目告诉我们，方程x2-mx+1=0有两个实数根，这个条件你用了吗？

学生恍然大悟，原来自己在解题时把隐含条件忘了.

错误原因找到了，学生订正已不成问题.但我没有到此为止，而是借题发挥，引导学生继续探究.

探究2：设x1、x2是方程2x2-4mx+2m2+3m-2=0的两个实数根，当m为何值时，x12+x22有最小值？请求出这个最小值.

探究3：已知关于x的一元二次方程8x2+（m+1）x+m-7=0有两个负数根，那么实数m的取值范围是______.

探究4：设m是不小于-1的实数，使得关于x的方程x2+2（m-2）x+m2-3m+3=0有两个不相等的实数根x1、x2.

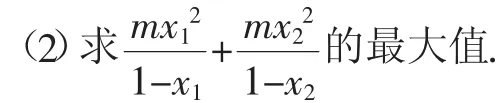
探究5：实数k为何值时，关于x的一元二次方程x2-（2k-3）x+（2k-4）=0：

（1）有两个正根？

（2）两根异号，且正根的绝对值较大？

（3）一根大于3，一根小于3？

以上由学生错解引发的探究，由浅入深，步步为营，不仅培养了学生思维的批判性，更培养了数学思维的深刻性，这正是教师所期待的理想效果.

马克思曾言：年轻人犯错连上帝也会原谅.因此，犯错并不可怕，只要教师善待这些“错误”，用好这些“错误”，同样可以成为学生的“财富”，也同样可以成为教师教学的“宝贵财富”.