学材重构单元教学,研判学情相机施行
——以一节“二元一次方程组”起始课为例
☉江苏省南京市上元中学 王圣芸
我们注意到,最近三年来,由中国教育学会中学数学教学专业委员会推广的首届国家教学成果奖“自学·议论·引导”在全国开展了3次推广活动,该教学法主要倡导“单元教学”,特别是“三学”(学材再建构、学法三结合、学程重生成)得到很多一线教师的积极响应,近年来在《中学数学(初中版)》能检索出相当数量的文献.然而我们也注意到,因为对单元教学的理解比较肤浅,教学实践时往往表现出一些“只见其形,未得其神”的尴尬课例.本文先梳理近期教学观摩所见的一节“二元一次方程组”单元起始课的教学流程,并跟进评课与商榷意见.
一、“二元一次方程组”单元起始课教学概述
教学环节(一) 实际问题,引入新知
问题背景:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.
问题1:篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,某队在一次比赛中胜x场,负y场,得到16分,你能得到怎样的关系式?
教学组织:学生列出方程2x+y=16.教师跟进追问这是什么方程,类比一元一次方程的定义,引导学生归纳定义出这是二元一次方程,并形成课题与板书.接下来安排一组练习,巩固二元一次方程的概念,以及如何灵活变换不同表示方法.
跟进练习:(1)在方程x+y=10中,用x表示y,得______,用y表示x,得______.
(2)在方程x-2y-1=0中,用x表示y,得______,用y表示x,得______.
(3)在方程3x-2y=1中,用x表示y,得______,用y表示x,得______.
教学环节(二) 列表研究“不定方程”的解
探究:满足方程2x+y=16,且符合问题实际的解:

表1
跟进练习:列表探究方程x+y=10的自然数解:

表2
教学组织:通过列表分析实际问题的解,发现在表格中有一组“公共解”,为进一步定义二元一次方程组的解提供了一个归纳的情境.并通过PPT呈现图1:
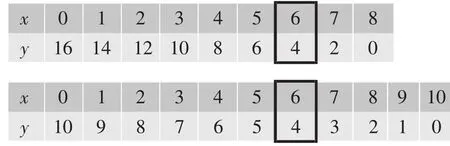
图1
在此基础上归纳出二元一次方程组的解的定义.
顺便将开课阶段的问题情境适当改编呈现,如下:
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,某队在10场比赛中得到16分,那么这个队胜、负场数分别是多少?
学生就可发现上面列表发现的那一组公共解就是这个实际问题的解.
教学环节(三) 研究“消元”解二元一次方程组
例1 用加减消元法解下列方程:
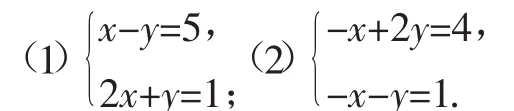
例2 用代入消元法解下列方程:
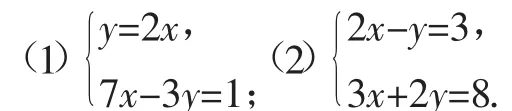
教学组织:教师准备了上述两组例题,结果因为教学时间不足,只能“匆匆示范”,学生是否真正掌握、深刻理解消元思想,因为没有见到有质量的对话与展示,难以评价.
教学环节(四) 完善生成“结构化板书”
教师根据本课所学,将主要内容和黑板上已形成的部分内容进行关联、转化,形成如图2所示的结构化板书,成为结课阶段一个教学亮点.
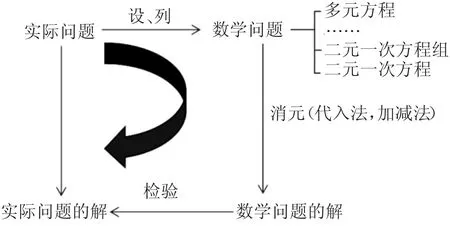
图2
二、评课与商榷
教学研究的经典话题一般是“教什么”“教谁”“怎么教”.这些我们熟悉的教研观点被国外包装为所谓的PCK理论,再经由国内一些数学教育专家学者的推介,成为目前引发关注的MPCK研究.事实上,通俗来说,就是教学内容,对学情的研判,如何组织教学.以下就围绕这三个方面,对上面的课例进行评析与商榷.
1.学材再建构的前提是深刻理解教学内容
这里所指的“深刻理解”就是被郑毓信教授反复推介的旅美数学教育研究者马立平博士在名著《小学数学的掌握与教学》中提及的“深刻理解”,即追求数学知识的深度、广度与贯通度.以二元一次方程组为例,消元求解二元一次方程组当然是全章核心内容,但是二元一次方程(组)的定义,它的相关概念如二元一次方程(组)的解,如何验证一组数对是否为某二元一次方程的解也是十分重要的准备知识.不可像上文课例中一样,“一带而过”.事实上“精彩是不容错过的”,比如,师生在得出二元一次方程的定义之后,可联系、类比一元一次方程的定义、一般形式(形如ax+b=0,其中a≠0),给出二元一次方程的一般形式ax+by=c(其中a、b、c为常数,且a、b不能为0),二元一次方程组的一般形式c、m、n、k为常数).也许有老师说,教材上都没有给出它们的一般形式,为什么一定要补充?这就需要我们想清这类一般形式在整个数式、方程学习征途中的前后一致性.学生以后会学习一次函数的一般形式、一元二次方程的一般形式、二次函数的一般形式,在七年级是有必要或值得向学生补充这些简单方程或方程组的“一般形式”的.
2.基于学情,适合的教学内容才是好的
如上所述,单元教学是基于深刻理解数学知识的前后一致、逻辑连贯而预设的,但在具体教学实施时,还需要考虑和研判学情,不能将课前的所有预设全盘托出,“完成所有课前预设”的教学是糟糕的,因为心中只有教学设计,而没有了学生和学情的观察与研判.这样来看,课前的预设要尽可能采取开放式教学的问题设计,比如,安排让学生讨论二元一次方程组的解法时,就需要一些十分简单的二元一次方程组,以便学生能从不同角度快速消元、转化成功,而不宜在起始课就给出复杂形式的二元一次方程组,也不宜一下子推出多个二元一次方程组安排学生来求解,因为本课主要任务是生成新知、定义新知、理解新知、运用新知,而新知的重点内容体现了二元一次方程及解的概念、二元一次方程组及解的概念,学生理解“公共解”的意义,并能分析一组有序数组是否为方程组的公共解.可见,在上文课例中给出两组用消元法解二元一次方程组的习题是超量的,使得教学主题发生偏离,需要删减,将更多的教学时间让位于前面概念的归纳与理解巩固.
3.预设开放教学,相机停留与推进学程
南京大学哲学系郑毓信教授倡导“从开放题走向开放式教学”,在一线教学实践中并没有得到太多的关注,原因是多方面的.笔者认为,开放式教学之所以难在一线教师中推广,与当前“习题单”式的导学案营造的教学生态有很大关系,这类导学案习题量大,数学课堂被大量、密集的习题占据,教师也就不可能有开放式教学.二是,开放式教学需要教师展开追问与即时评价,而这些都对教师专业基本功提出了很高的要求.但是,我们并不能因为难就放弃开放教学的追求与努力,而应该作为心向往之的努力目标.具体来说,开放式教学所设计的问题需要精心准备、打磨,比如,安排学生探究二元一次方程的解时,可以先充分放开探究任意数组,只要满足方程的等式成立,然后限制到考虑正整数解,这样符合要求的有序数对就很有限了,便于学生很快发现,而且教师也能充分驾驭、即时点评、跟进追问、引导学生互评.
三、写在后面
单元教学是当前教研热点,但是教学研究并不是简单的“蹭热点”,而要真正静心阅读与实践反思(相关建议可参阅郑毓信教授的文献[3]),想清单元教学的课前用力点何在,如何基于理解数学、理解学情、理解教学来优化教学设计,真正让课堂简约起来、开放起来,是值得我们认真思考的.当然,所有的努力都会指向我们的专业基本功的精进与发展.

