用于相机标定的两种优化策略

于晓敏

（四川大学计算机学院，成都 610065）

0 引言

随着数码科技的发展和相关产品在生活中的应用范围不断扩大，相机标定技术的重要性日益增加，并且在机器人视觉、虚拟现实等领域相机标定有着广泛的应用，特别是对于在特征点稀疏的简单场景下的相机标定有着越来越大的需求。要解决相机标定问题，必须通过一些途径来获取空间点和图像点的对应关系，这种对应关系是由空间中相机的位置及其成像的几何模型所决定，即由相机的外部参数和内部参数所决定，这些参数必须由试验与设计来确定。

本文针对上述应用本文提出一种只需根据少量信息就能确定相机外部参数的方法。因为本文的重点是给出一种优化策略，所以假设已经通过某些途径获取到了相机外参和特征点深度的初值粗略值。常见的相机外参初值获取方法是5对点法[1]和8对点法[2]。在此初始化的基础之上利用三角测量[3]来获得特征点的初始深度。在获得相机参数和特征点深度的初始值之后本文根据相机与点对的几何关系来构建最小二乘问题对相机外参和特征点深度做第一步优化。与其他方法不同的是本文的第二步优化不是利用重投影误差信息，而是利用光度误差信息。

1 非线性最小二乘

考虑一个简单的最小二乘问题：

这里 x∈Rn，f是任意非线性函数，设它有m维：f(x)∈Rm。如果 f是个数学形式上很简单的函数，则可以令目标函数的导数为零，然后求解x的最优值，但是在本文中使用李代数来表示相机的旋转与平移，这将使得不能顺利的求解这样一个复杂的方程。所以本文利用迭代的方法，从一个初始值出发，不断的更新当前的优化变量，使目标函数下降。即对于第k次迭代，寻找一个增量Δxk，使得 f(x+Δxk)达到极小值，若Δxk足够小，则停止，否则，继续迭代。

这让求解导函数为零的问题变成了一个不断寻找梯度并下降的过程，直到某个时刻增量非常小，无法再使函数继续下降，目标达到了一个极小，整个过程完成。所以整个过程的关键之处就是Δxk如何确定。

本文使用高斯牛顿法来求解增量。它的思想是将f(x)进行一阶的泰勒展开，即：

这里J(x)为 f(x)关于 x的一阶导数，实际上是一个的矩阵，也是一个m×n的雅克比矩阵。要求解的变量Δxk由高斯牛顿方程直接给出：J(x)TJ(x) Δxk=-J(x)Tf(x)，至此，对于J(x)的求解已经成了本文的关键所在。

2 基于任意点对之间的几何关系进行优化

本文根据相机外部参数与标定点对之间的几何关系[4]提出一种优化策略，以此来做第一步优化。此次优化只针对旋转矩阵R进行优化。

2.1 相机外部参数与标定点对之间的几何关系

如图1所示，假定某个标定参照物上有n个标定点G0,G1,…Gn，它们之间的位置关系是任意的，且是已知的，在本文中它们的初始位置关系由特征点深度信息的初始值给出。

图1 相机与点对的几何关系

在图1中C点表示当前帧的相机中心，标定点Gi,Gj,Gk的初始位置关系在参考帧中已知。Gq(q =1,2…n)在当前帧相机坐标系下的正规化图像坐标[gqx,gqy,1]T是已知的。假设选取Gi,Gj为待处理点对，则可以得到：

其中表达式R∙GiGj表示将向量GiGj由参考帧坐标系变换到当前帧坐标系，R是待优化的旋转矩阵。

记：

由式（1）可得：v(x)=0，这里x表示由旋转矩阵组成的向量。当然，由于噪音的存在，我们估得的R不一定精确的使式（2）为零，所以更常见的做法是求一个最小二乘问题。按照之前的分析，接下来的需要求出v(x)相对R的雅克比矩阵J(x)用以指导优化方向。

2.2 雅克比矩阵的求解

由于旋转矩阵R的自身约束，即R∈R3×3且RRT=I,det(R)=1，导致求解上的一些限制，所以本文中将以无约束的李代数形式来表示旋转。旋转矩阵R对应的李代数是定义在R3上的向量，记作φ。对于每一个φ，都存在一个反对称矩阵Φ，使得下属等式成立：φ1,φ1,φ1∈R3。

根据李代数φ与旋转矩阵R之间的映射关系：R=exp(φ∧)，则式（2）可写为：

其中向量φ为φ=[ ]

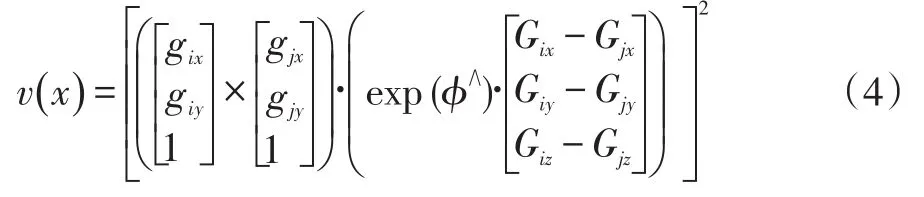
对于三维向量φ，记它的模长和方向分别为θ和a，于是有 φ=θa，a=[a1,a2,a3]∈R3这里a是一个长度为1的方向向量。

将李代数φ与旋转矩阵R之间的映射关系按照泰勒展开可写为：

经计算可得：

为了方便，记：

那么由式（4）（5）（6）可得到：

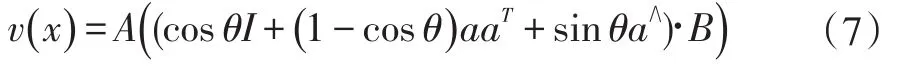
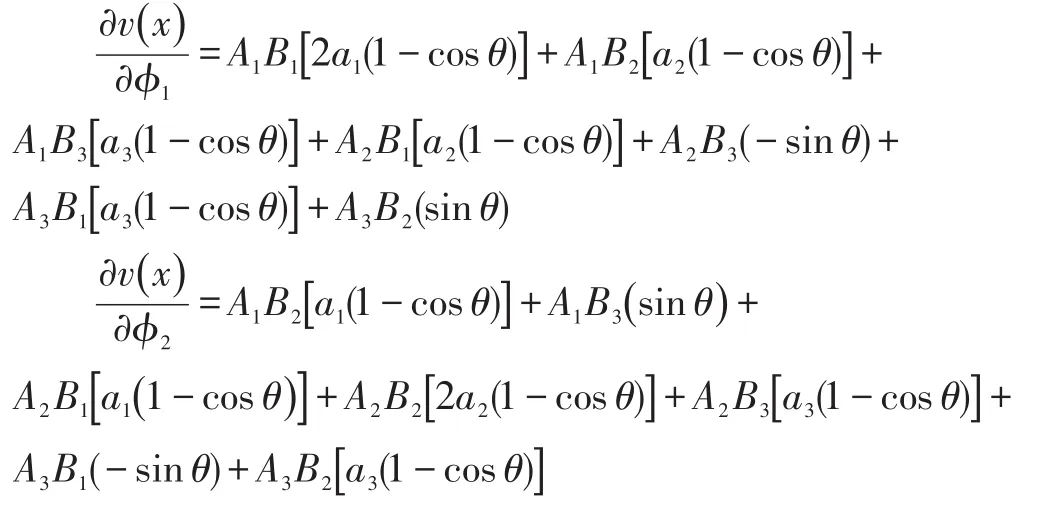
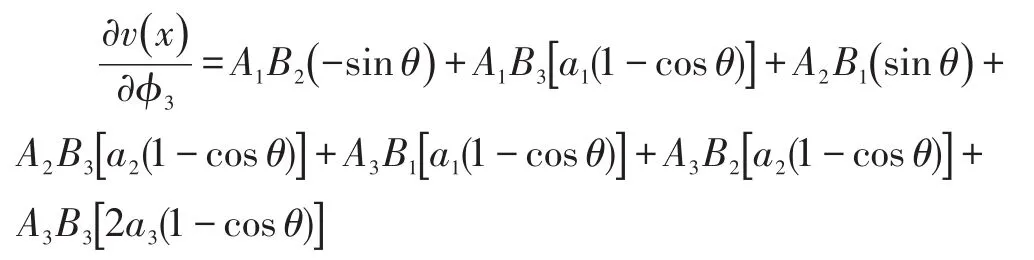
其中Ai,Bi(i=1,2,3)表示向量A,B的第i个元素。

3 基于光度误差信息的优化

图2 投影示意图

如图2所示，p1,p2为同一空间点在不同图像上的投影点，由于误差的存在，p2的外观和 p1会有明显的差别。为了减小这个差别，我们来优化相机位姿和空间点的位置，来寻找与 p1更相似的 p2。记e=I1(p1)-I1(p1)为两个像素的光度误差，所以优化目标为：

其中ξ∈R6表示的是变换矩阵T∈R4×4的李代数形式。能够做这种优化的理由是灰度不变假设，即假设一个空间点在各个视角下成像的灰度是不变的。为了求解这个优化问题，本文关心的是误差e关于相机位姿ξ和空间点P的导数，即相应的雅克比矩阵。

3.1 关于相机位姿ξ的雅克比矩阵

为了求解误差e关于相机位姿ξ的雅克比矩阵，需要分析它们的导数关系，因此使用李代数上的扰动模型，给 exp(ξ)左乘一个小扰动 exp(δξ)，并使用定义在李代数上的加法，得：

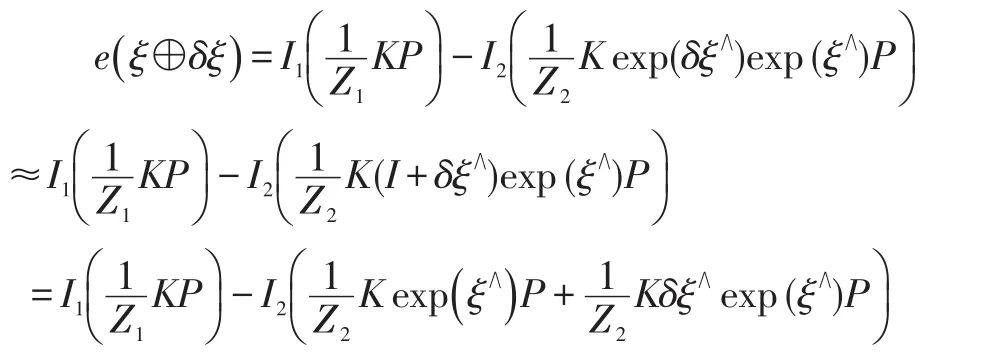
记：

这里q为扰动分量在第二个相机坐标系下的坐标，而u为它的像素坐标，利用一阶泰勒展开，有：

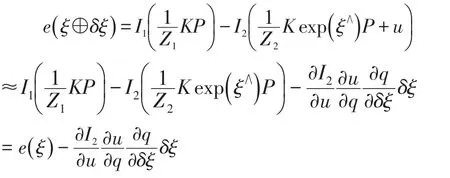
可以看到，一阶导数由于链式法则分成3项，而前两项都是容易计算的，记q=[X ,Y,Z]T，那么有：

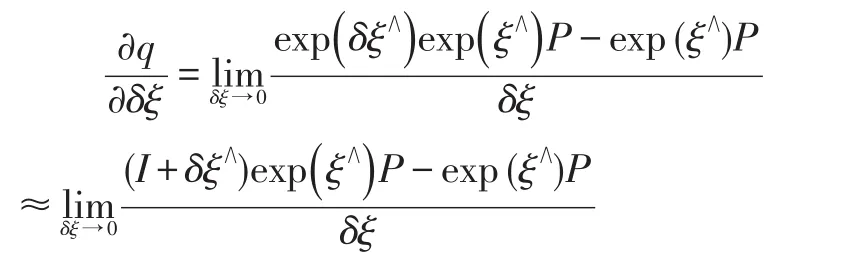
3.2 关于空间点位置 PP的雅克比矩阵

假设空间点P=[X ,Y,Z]T在不同图像上的投影点为U1和U2，且经过欧氏变换之后它的空间坐标为P'=[X',Y',Z']T，则光度误差可表示为：

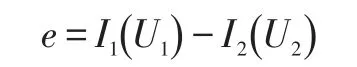
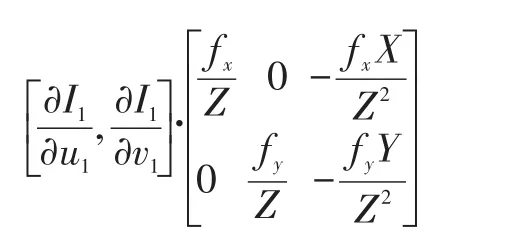
第二项可表示为：

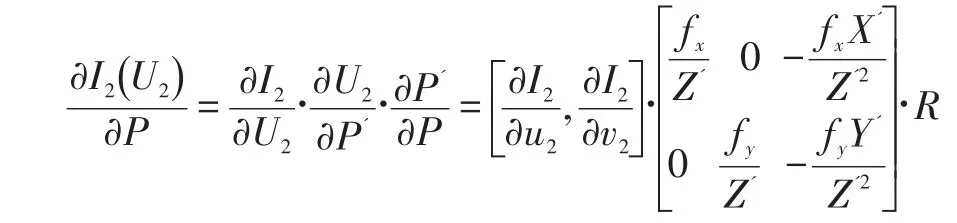
4 试验与分析

试验使用的优化库是g2o，相机的内部参数为：fx=929.992,fy=927.169,cx=671.617,cy=384.836。试验选取一个特征点较少的场景，如图3所示。

图3 试验场景图

相机外参的估计及优化结果由表1给出，使用重投影误差来衡量优化精度。

对于空间点的估计及优化结果由图3给出，试验中将从深度相机采集的特征点深度与从本文得到的特征点深度进行对比。由于这里的深度值丢失了尺度信息，所以本文比较的是深度信息两两之间的比值。任取若干个特征点，记从深度相机采集的特征点深度为di(i=1,2,3…)，从本文得到的特征点深度为di'(i=1,2,3…)，假设，，结果如图4所示。

表1 试验结果

图4 深度估计结果

5 结语

本文首先通过其他途径求出相机位姿及特征点深度的初始粗略值，然后通过两步优化对相机外部参数和特征点深度进行调整，以达到较高精度，针对这两步优化，本文分别给出相应待优化量的雅克比矩阵，用以找迭代的梯度方向，从而达到优化效果。从试验结果可以看出，即使是清水房这样的特征点少的简单场景本文的方法仍能达到较好的效果，并且该方法原理简明，方便实用。