改进Hausdorff距离和粒子群的图像配准算法

胡明娣, 张中茂, 许天倚, 杨 洁

(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

图像配准[1]是指在同一视觉系统中寻找一个最优变换，使得在不同环境下获得的参考图像和待配准图像高度吻合，对应特征点一一映射，即对齐的空间位置达到最佳。图像配准技术已广泛应用于导航及遥感图像处理等领域。

图像配准方法主要分为基于特征和区域两种类型。基于特征点的图像配准方法对噪声及遮挡等干扰具有适应性强和数据计算量少等优点，应用较为广泛[2]。Hausdorff距离(Hausdorff distance,HD)[3]作为目前较为常用的图像特征匹配度量，对图像畸变适应性强，已取得较好的效果。基于代价函数(least trimmed square-Hausdorff，LTS-HD)距离的图像配准算法[3]通过设定距离阈值去除噪声点及错误距离，将改进的Hausdorff距离作为匹配测度，虽然取得了较高的配准率，但其阈值设置依靠经验，且复杂度较高。文献[4]实现了对遮挡图像自适应遮挡系数调整的Hausdorff距离测度，但是只适用于图像中能提取大量特征点的图像配准，不具有通用性。基于分割模板加权Hausdorff 距离矩阵的特征匹配算法[5]，在图像内容分布对比较明显时取得了较高配准率，但模板加权系数很难确定。文献[6]综合考虑了遮挡系数、代价函数和出格点，改进了Hausdorff距离，并结合量子遗传算法实现异源遮挡图像配准，但其只适合激光图像的配准，应用领域狭窄。

本文针对异源遥感图像部分遮挡情况，利用尺度不变特征变换(scale-invariant feature transform,SIFT)算子[7]提取图像的SIFT特征点作为图像匹配特征空间，通过融合标准方差及部分平均改进Hausdorff距离作为相似性测度。同时，在粒子群(particle swarm optimization,PSO)算法[8]基础上引入自适应参数和扰动机制增强算法的寻优性能，并将该算法作为图像配准的搜索策略，以期达到更好的配准效果。

1 改进的Hausdorff距离测度

1.1 Hausdorff距离

Hausdorff距离是一种模糊距离测度，用来衡量两个有限点集之间的相似度。在图像匹配识别中，将图像作为一个点集，图像的匹配程度则用两个点集的相似程度表示。当两点集之间Hausdorff距离越小时，两点集的相似程度就越大。点集A={a1,a2,…,ap}到点集B={b1,b2,…,bq}的Hausdorff距离[9]定义为

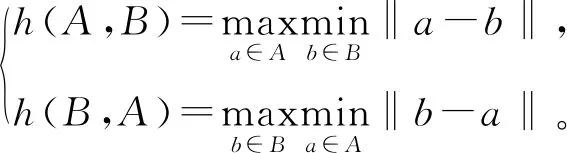
式中：h(A,B)和h(B,A)分别表示点集A到点集B和点集B到点集A单向的Hausdorff距离；‖·‖为距离二范数。

1.2 改进的Hausdorff距离测度

部分Hausdorff距离(partial Hausdorff distance,PHD)[9]和平均Hausdorff距离 (modified Hausdorff distance,MHD)[10]对图像噪声具有较好地适应性。结合部分平均及排序思想，并融合标准方差，对Hausdorff距离进行改进，得到改进的部分均值Hausdorff距离 (improved partial modified hausdorff distance,IPMHD)，可定义为

式中：hz(A,B)为点集A到点集B有向距离由小到大排序后第z个Hausdorff距离值；hz(B,A)同理；S(A,B)和S(B,A)分别为两点集之间的标准方差；NA和NB分别为点集A和点集B中特征点数目；f为遮挡比例；修正系数e通常取0.9[4]；q和p分别为点集A和点集B中实际计算所用特征点个数。

改进的IPMHD距离测度取值既不是点到集合最小距离，也不是最小距离中最大值，集合中所有点并未全部用于计算，剔除由孤立点造成的大距离，对剩下部分点排序，再采用部分点取平均。IPMHD考虑了遮挡对图像匹配效果的影响，因而对遮挡及异常值适应性较强。

2 扰动机制的自适应参数PSO算法

2.1 基本PSO算法

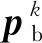
(1)

(2)

2.2 Levy飞行机制

Levy飞行机制[11]使运动的轨迹具有随机性，飞行中频繁的短距离搜索可在当前最优解周围仔细搜寻，以此提高局部搜索能力；利用偶尔长距离的跳跃式搜索可扩增搜索范围增强粒子全局搜索,防止粒子陷入局部最优解。引入Levy飞行机制后，粒子的位置可更新[11]为

(3)

其中：ϑ为步长控制量；L(β)为莱维随机搜索路径的随机数。ϑ和L(β)需满足条件[11]为

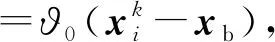
其中：ϑ0为常数，通常取0.01[11]；β取值范围为[0，2]；xb为所有粒子中位置最优处;μ和ν为服从标准正态分布随机数;Γ为标准Gamma函数。

2.3 Logistic混沌机制

Logistic混沌机制[12]使粒子处于混沌状态，因而能扩大粒子的活动范围。当粒子陷入局部最优时，将Logistic混沌机制引入PSO算法，可增加粒子种群多样性，从而避免算法过早收敛，达到寻优目的。更新后的粒子位置表示式[12]为

(4)

其中：zk表示混沌域，且zk∉(0.25,0.50,0.75)时系统处于混沌区域；α为Logistic参数，取值范围为(0,4]，当α∈(3.569 945 6, 4)时，系统处于混沌状态[12]；λ为扰动系数，一般取值为常数2[12]。

2.4 扰动机制的自适应参数PSO算法

改进的粒子群算法(improved particle swarm optimization,IPSO)通过动态改变PSO算法中惯性因子和学习因子，添加Levy飞行和Logistic混沌两种扰动机制，扩展种群多样性，避免陷入局部最优。

惯性权重因子采用余弦变化[13]，可表示为

(5)

加速因子采用正弦函数变化[14]，可表示为

(6)

其中：ωmax=0.95,ωmin=0.40；g为总迭代次数;r1和r2为0～1之间的随机数;c=1.5为基准值。PSO算法搜索前期，ω取值较大，加速因子c1大、c2小，有助于个体对全局学习；后期ω取值较小，加速因子c1小、c2大，有助于局部搜索时群体的学习。将式(5)和式(6)分别代入式(1),得到粒子更新速度为

(7)

3 基于IPMHD测度的IPSO图像配准

将IPSO算法用于特征点匹配搜索策略，以IPMHD距离测度作为IPSO适应度函数，根据基准图规格确定粒子活动边界范围。使粒子群在基准图上随机搜索，每次动态记录粒子所在位置，并以该点位置为左上角截取尺寸大小与模板图相同矩形区域，每次截取的矩形块与模板图之间的IPMHD距离为本文算法可行解，所有可行解中的最小的IPMHD即为最优解，输出最优解值并结束算法。基于IPMHD测度的IPSO图像配准算法的具体步骤如下。

步骤1设置初始参数，以IPMHD距离测度为IPSO算法适应度函数。

步骤2初始化粒子，计算粒子适应度函数值f(xi)，记录个体最优值pb及种群全局最优值pg。

步骤3利用式(7)和式(2)更新粒子。

步骤5引入Logistic混沌扰动,利用式(4)对粒子位置更新。

步骤7引入Levy飞行扰动，利用式(3)更新粒子位置。

步骤8记录粒子适应度值，并更新个体最优值以及全局最优值。

步骤9判断是否达到最大迭代次数，若是，则输出pg，停止迭代，算法结束；否则转入步骤3，重复迭代。

4 实验及结果分析

实验在Win10环境下，CPU为Intel Core i7-8 700 K,主频为3.7 GHz,内存为16 GB的仿真平台上，使用Matlab R2016a软件进行仿真，验证IPMHD距离的有效性和IPSO算法的配准性能。以IPMHD距离测度为IPSO搜索算法适应度函数，适应度函数值越小，粒子适应性更优。

4.1 无遮挡条件下Hausdorff距离匹配性能对比

为了验证IPMHD测度的有效性，分别使用两组数据进行验证。第1组数据为通过GoogleEarth下载的两幅615×600像素的青海湖鸟瞰图，如图1所示；第2组数据为地理空间数据云下载的Landsat TM不同单波段异源图像，其规格为620×600像素，并截取子图150×150像素，如图2所示。将IPMHD、HD、PHD 、MHD和LTS-HD等5种测度分别进行仿真匹配，比较其无遮挡条件下图像配准成功率，结果如表1所示。

图1 同源未遮挡遥感图像配准结果

图2 异源遥感图像配准结果

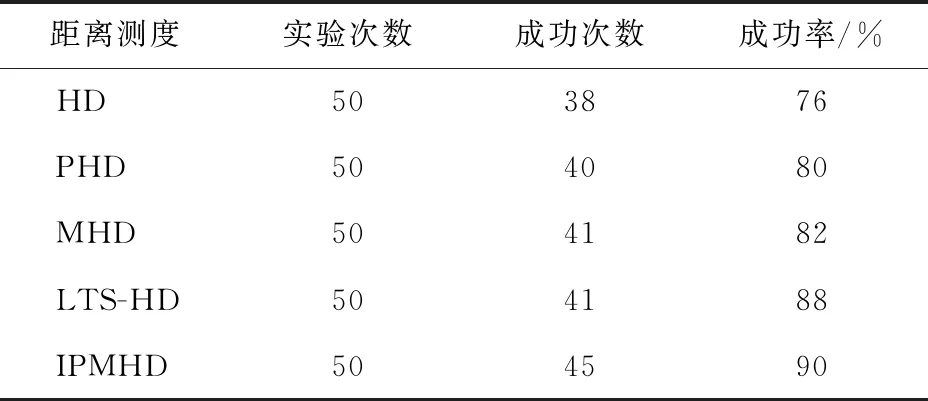
距离测度实验次数成功次数成功率/% HD503876 PHD504080 MHD504182 LTS-HD504188 IPMHD504590

由表1可以看出，HD距离测度匹配效果最差；PHD和MHD距离测度性能接近，较HD距离有一定提高；LTS-HD距离测度优于HD、PHD和MHD距离测度；IPMHD距离测度匹配性能相较LTS-HD距离测度有小幅提升，性能最优。

4.2 遮挡条件下各Hausdorff距离匹配性能对比

为验证IPMHD算法对遮挡适应性及鲁棒性，选取Landsat4-5 MSS多波段卫星图作为异源图像对，图像规格为761×748像素，如图3所示，其中图3(b)为图3(a)中截取200×200像素子图；图3(d)为图4(c)的遮挡40%，图3(e)为图3(b)和图3(d)之间的配准。分别将IPMHD、HD、PHD 、MHD和LTS-HD等5种测度根据图3中的配准图进行不同比例遮挡实验，5种Hausdorff距离测度在遮挡条件下的图像匹配成功率如图4所示。

图3 异源遮挡遥感图像配准结果

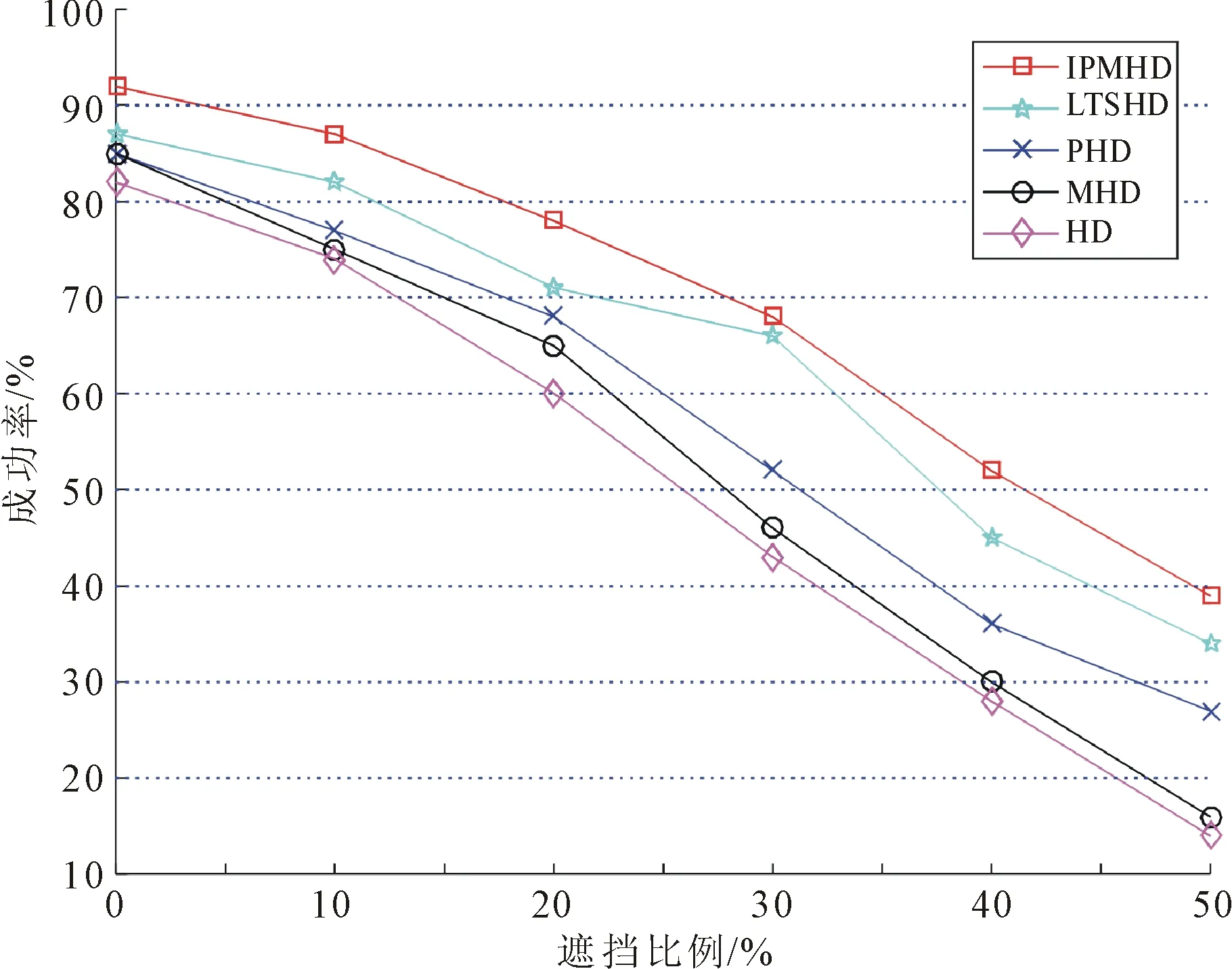
图4 各距离测度在遮挡条件下的图像匹配成功率

从图4可以看出，各Hausdorff距离测度随遮挡比例提高配准成功率呈下降趋势。 HD、PHD和MHD在遮挡比例超过20%时，性能急剧下降；LTS-HD考虑了遮挡和异常值的影响，但遮挡适应性略低于IPMHD；IPMHD距离测度对遮挡的抗干扰性最强，当遮挡比例不超过20%时，仍有高达近80%成功匹配率，且对于排序靠前的前z个特征点，前40%的点对配准有用，因此可取IPMHD距离从小到大排序前40%特征点，以减少运算量。

4.3 配准算法比较分析

以IPMHD距离为相似性测度，分别将IPSO算法、文献[13]、文献[14]和文献[15]中的改进PSO算法作为搜索策略进行配准实验，寻优结果如表2所示。

表2 不同搜索算法寻优性能对比

由表2可以得出，文献[13]和文献[14]算法在性能及时间上比较接近，在耗时上优于文献[15]算法及IPSO算法，但寻优结果稳定性较差；IPSO耗时比文献[15]算法长，可能是因为两次扰动的随机性耗时较长，但成功匹配次数最高，寻优准确率高于其他3种算法，具有较强的实时性。

上述3组实验均证明了在图像受干扰时，IPMHD距离测度比其他改进的Hausdorff距离测度适应性更强，同时IPSO算法相比其他改进PSO算法寻优性能更佳。

5 结语

以异源遥感图像为背景，分别改进了Hausdorff距离测度和粒子群算法的图像配准算法，将图像的SIFT特征作为特征空间，融合部分平均和标准方差改进hausdorff距离，改善了Hausdorff距离易受干扰等缺点；选择粒子群算法作为搜索策略，引入自适应变换参数改变惯性因子和学习因子，同时加入扰动机制改变粒子位置，防止了粒子陷于局部最优。实验结果表明，IPMHD距离测度比其他改进的Hausdorff距离测度适应性更强，IPSO算法相比其他改进PSO算法，寻优性能更佳。该图像配准算法具有较好地图像配准效果。