多目标混合优化的阈值图像分割
赵 凤, 孔令润
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.电子信息现场勘验应用技术公安部重点实验室, 陕西 西安 710121)
图像分割的目的是根据特定的标准将图像分成若干具有独特性质的互不相干区域,使得同一区域内的像素特征具有较高相似性,而不同区域的像素特征具有较大差异性[1]。图像分割是图像处理的重要一环,其结果会直接影响到后续图像处理的质量。
现有的图像分割方法主要包括基于阈值[2]、基于聚类[3]和基于区域的分割方法[4]等几类。基于阈值的图像分割是一种常用的分割方法。图像阈值是指从背景中提取出的场景对象,有助于分析和解释图像。基于阈值的图像分割算法假定图像的直方图呈双峰分布,通过在两峰之间确定某一准则来选择一个恰当的阈值,便可实现图像的目标和背景的分离。Otsu最大类间方差法[5]、最大熵法[6]和模糊熵法[7]等是比较常用的阈值分割方法。Otsu最大类间方差法利用最大化分割后图像的类间方差来选取最佳阈值,其原理简单且对大多数图像都能获得较好的分割结果。然而,当图像直方图没有明显的双峰时,最大类间方差法的分割效果不佳。由于很多图像的特征信息具有模糊性,因此有学者以香农熵为基础,结合图像的模糊数学描述,提出了图像模糊熵的概念并将其应用到阈值图像分割中[8]。在进行多阈值图像分割时,由于模糊隶属函数包含的参数较多,取值范围较大,导致该方法分割效果不佳且计算量较大[9]。
为了降低计算量,群智能优化算法被用到图像分割中[10-13]。常见的群智能优化算法有粒子群优化(particle swarm optimization, PSO)算法[14]和蚁群优化(ant colony optimization, ACO)算法[15]等。如文献[10]针对二维Otsu算法计算量过大的缺点,采用PSO算法寻找最优的二维阈值向量,在取得较为理想分割结果的同时,减小了计算量。文献[12]提出了基于最小交叉熵的萤火虫阈值图像分割算法,对多阈值图像可以得到良好的分割结果,并且缩短了计算时间。这些启发式算法虽然算法简单,易于实现,但在迭代后期易陷入局部最优,从而影响了分割效果。
为了避免陷入局部最优,多元宇宙优化(multi-verse optimization, MVO)算法[16]被提出,其具有参数少、结构简单、效率高等优点。由于MVO算法引入了动态参数来控制种群的进化,因此在迭代后期更容易跳出局部最优。在MVO算法的基础上,有学者提出了混合优化算法[17-18],如文献[17]结合PSO算法和MVO算法解决全局数值优化和无功优化调度问题。然而,上述方法只考虑了一个目标函数,当面对多目标优化问题时,应用受限。
近年来,多目标优化算法被应用到阈值图像分割[19-21]中,如文献[19]结合多目标粒子群优化提出了一种基于支配和多样性准则的多目标阈值分割算法。文献[21]结合多元宇宙理论,将类间方差函数和最大熵函数作为待优化的目标函数,提出了基于多目标多元宇宙理论的阈值图像分割算法。不论是最大类间方差法还是最大熵法虽然易于实现,但对于目标和背景差异不明显的图像,分割效果不理想。
本文拟针对多目标、多阈值图像分割问题,提出一种引入混沌搜索的多目标粒子群和多元宇宙混合优化(chaos search-based multi-objective hybrid optimization combing particle swarm and multi-verse, CSMHO-PSM)的阈值图像分割算法。采用类间方差函数和模糊熵函数作为多目标优化的两个目标函数。将MVO算法引入到PSO算法中,引入混沌搜索策略,通过混合优化的方法得到更优解,避免陷入局部最优解。采用类内差异性与类间紧致性的加权比值来确定算法非支配解集中的最优解,实现多阈值图像分割。
1 基础理论概述
1.1 粒子群优化算法
PSO算法[14]源自于对鸟群捕食行为的研究,其首先在搜索空间内生成一组均匀分布的粒子Xi={Xi,1,Xi,2,…,Xi,D},(i=1,2,…,N),N表示种群规模,D表示粒子的最大维度。
粒子的速度决定飞行的距离和方向。由当前粒子经历过的最好位置(全局极值)以及所有粒子在每次迭代中得到的最好位置(个体极值)决定速度的更新过程。
粒子i在维度j的第t+1次速度更新过程[14]可以表示为
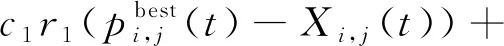
(1)

粒子i在维度j第t+1次的位置更新方式[14]可以表示为
Xi,j(t+1)=Xi,j(t)+Vi,j(t)。
(2)
假设优化问题是极小化问题,粒子i第t+1次迭代的个体最优解[14]计算公式为
(3)
其中f是目标函数。
全局最优解gbest的计算公式[14]
(4)
将粒子群算法应用到阈值图像分割中,能有效减小多阈值分割的计算量。
1.2 多元宇宙优化算法
MVO算法[16]是基于物理学中多元宇宙理论中的黑洞、白洞和虫洞等3个主要概念提出的群智能优化算法。白洞是一个只发射不吸收的特殊天体;黑洞刚好与白洞相反,它吸引宇宙中一切事物,所有的物理定律在黑洞中都会失效;虫洞作为连结白洞和黑洞的多维时空隧道,将个体传送到宇宙的任意角落,甚至是从一个宇宙到另一个宇宙。而多元宇宙通过白洞、黑洞和虫洞相互作用达到一个稳定状态。在优化问题中,假设每个解都是一个宇宙,每个解中的变量都是相应宇宙中的对象。MVO算法可以简单地归纳为以下几个步骤。
步骤1初始化宇宙数U和最大迭代次数q。
步骤2在每次迭代中,根据宇宙的标准膨胀率对宇宙进行排序,然后通过轮盘赌机制选择其中一个宇宙来建立一个白洞[16],其公式为
(5)

步骤3更新虫洞存在概率PWE和虫洞向最优宇宙移动的旅行距离率RTD。PWE和RTD的计算公式[16]分别为
(6)
(7)

步骤4计算当前宇宙膨胀率,若宇宙膨胀率优于当前宇宙膨胀率,则更新当前宇宙保存膨胀率,否则,保持当前宇宙。
步骤5更新宇宙位置,并在最优宇宙中寻找最优个体。其选择条件[16]为
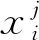
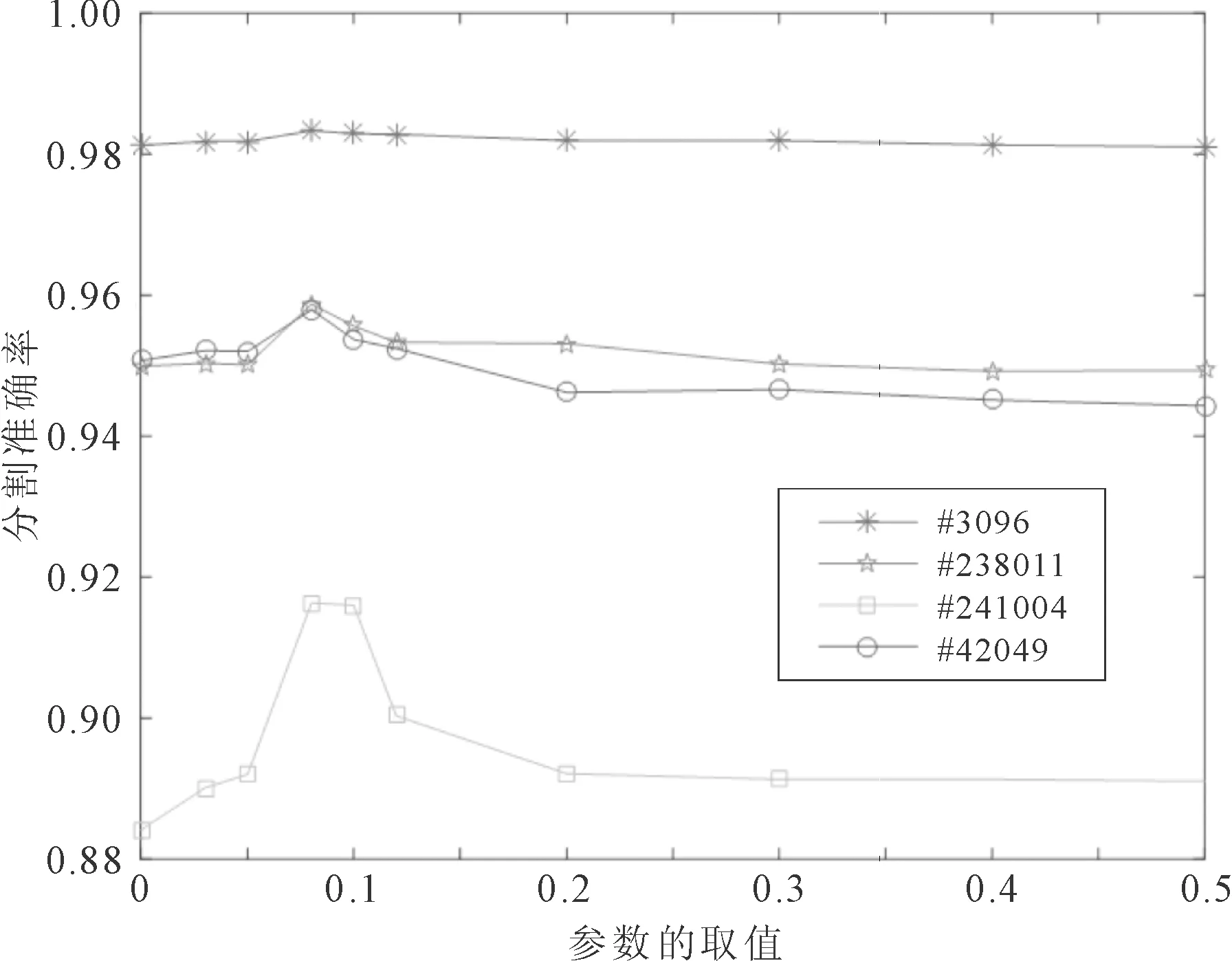
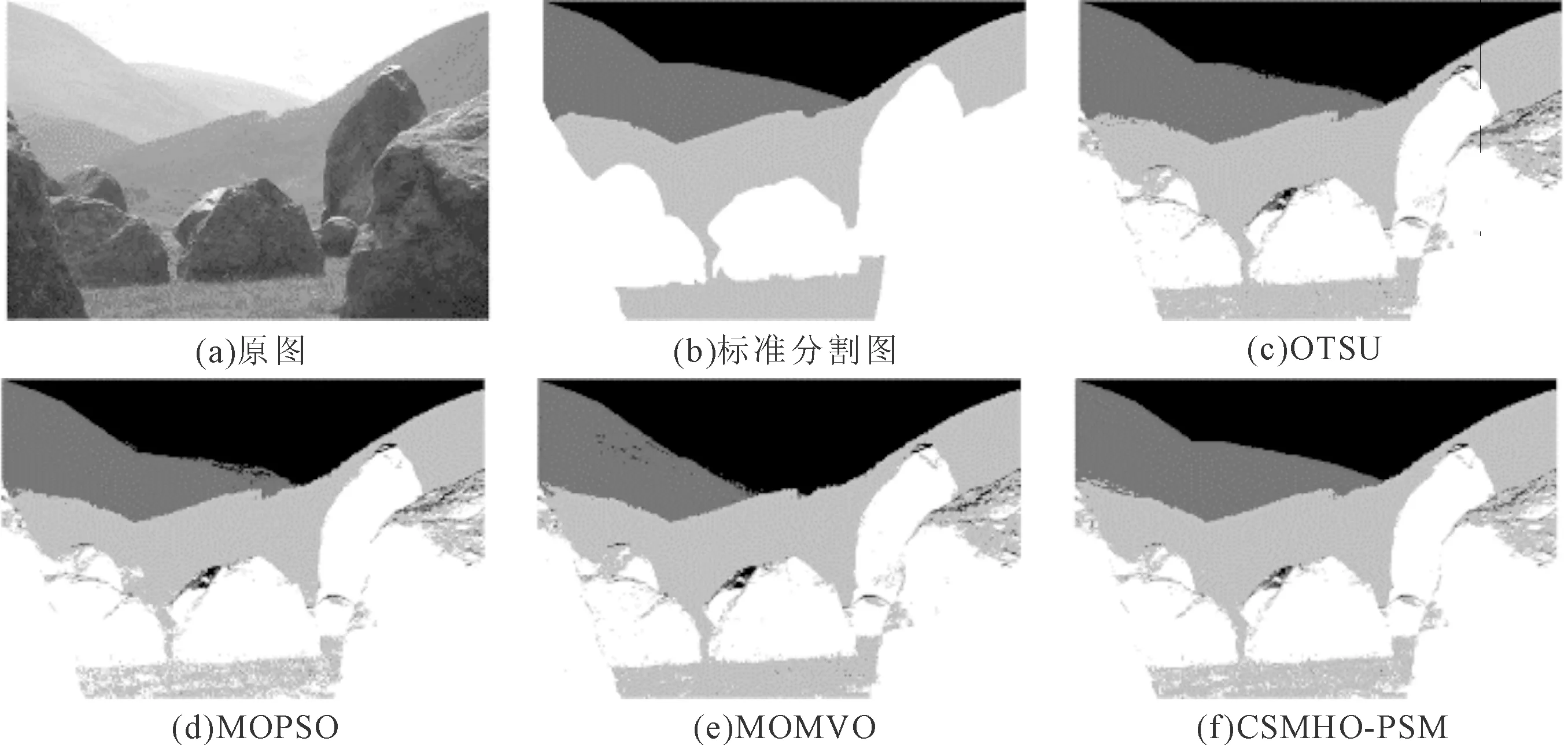
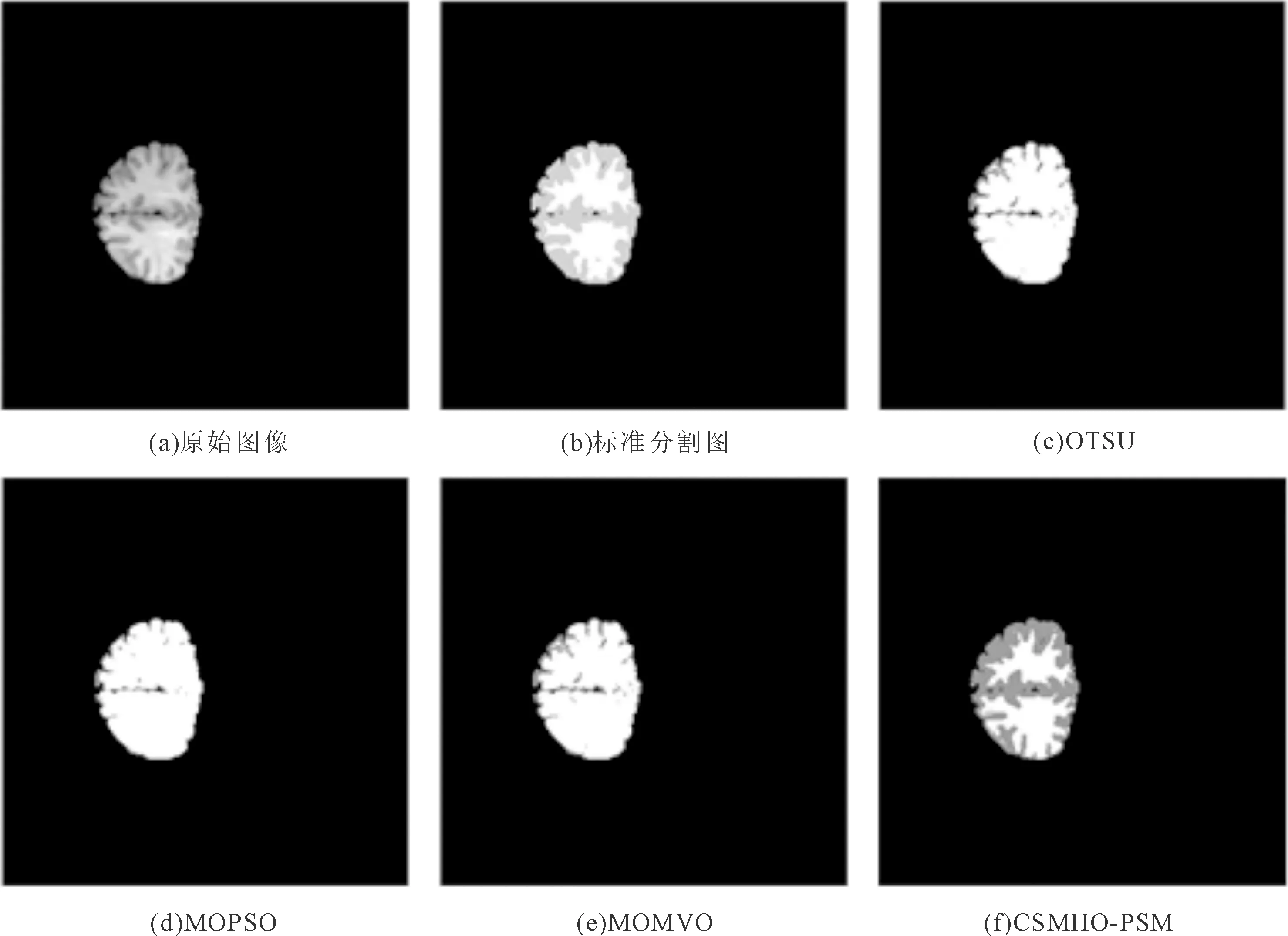
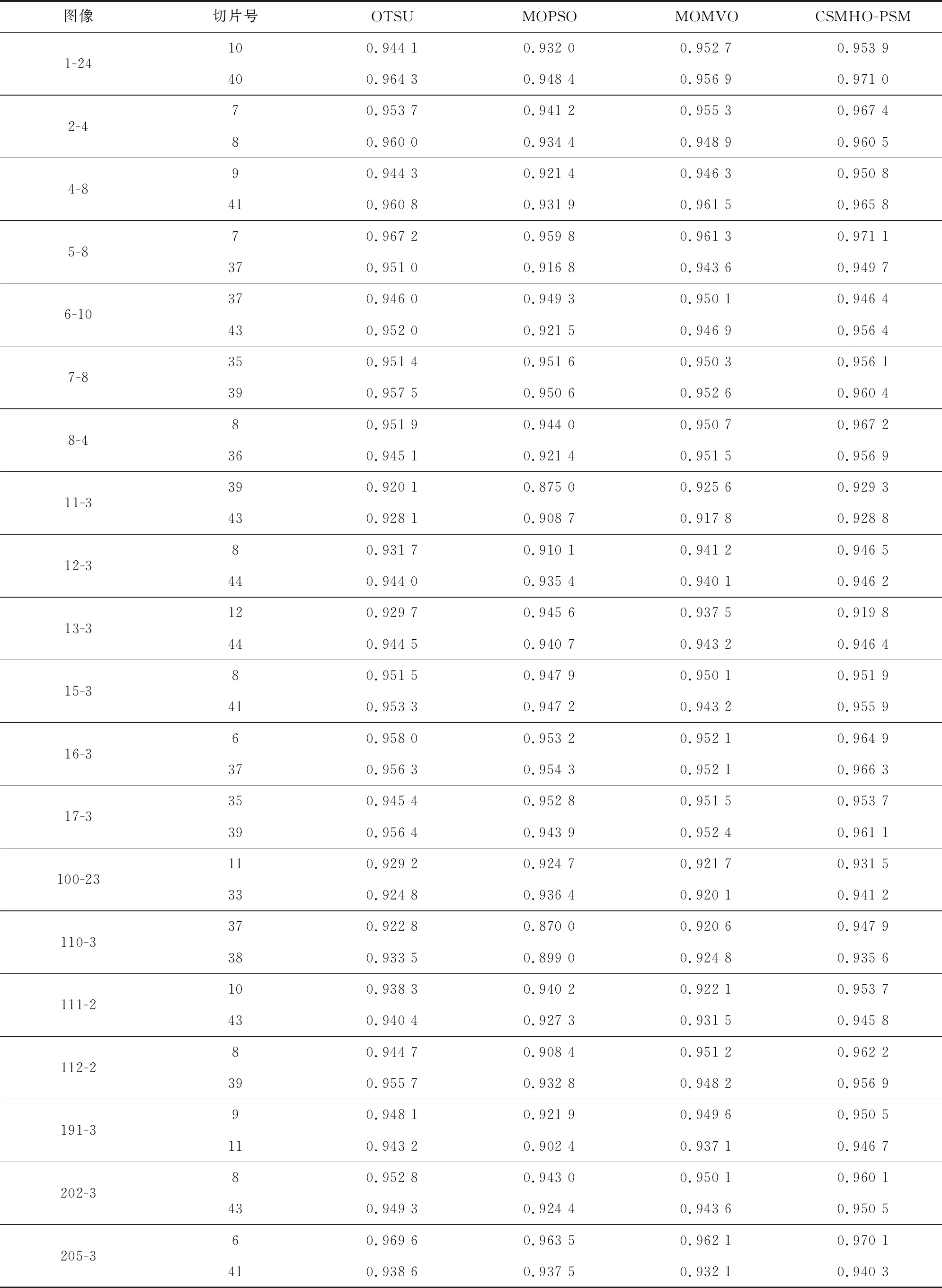
若r2 (8) 将MVO算法与PSO算法相结合能改善PSO算法在迭代后期易陷入局部最优的缺点。 混沌搜索[22]通过某种特定方式迭代产生混沌序列,然后通过载波的方式将混沌变量放大到优化变量的取值范围中,混沌搜索的过程如下。 首先随机初始一个D维的向量y0=[y0,1,y0,2,…,y0,D],0 yn+1,D=μyn,D(1-yn,D)。 (10) 其中:n∈[0,Nmax],Nmax为解的最大个数;μ是混沌状态的控制参数,μ取4时,Logistic方程完全进入混沌状态。 向量y0产生混沌序列后,通过载波的方式将混沌变量的值映射到优化变量的取值范围。然后实行载波操作将混沌变量放大,再加载于待搜索的个体变量上,从而得到新个体yn,D,生成公式[23]可以表示为 yn,D=fz,D(2yn,D-1)。 (11) 其中:fz,D代表待搜索个体;Rz,D为混沌搜索半径。 为了进一步提高阈值分割算法的精度,可以进行K次混沌搜索,以提高种群多样性,从而优化阈值图像分割的效果。 将类间方差函数和模糊熵函数作为算法的两个目标函数,并引入MVO算法来改进PSO算法易陷入局部最优的缺点。加入混沌搜索策略以提高算法的搜索精度,使其更加有效地逼近最优阈值。多目标进化后会产生一组非支配解,利用类间差异和类内差异的加权比值来选择最优解。 对图像阈值进行编码,编码方式为实数制编码,编码范围为[Imin,Imax],Imin和Imax分别表示图像像素的最小值和最大值。设算法中种群规模为g(g=1,2,…,N),其解的维度为e(e=1,2,…,D),则其种群初始解可表示为 Ig,e=Imin+r5(Imax-Imin)。 (12) 其中:Imin和Imax分别表示一幅图像像素灰度值的最小值和最大值;r5表示[0,1]之间的随机数。 采用类间方差函数和模糊熵函数作为优化的适应度函数。假设一幅图像总的像素数目为C,其灰度级h的取值范围为[0,255],具有灰度级h的像素个数为Ch,则灰度级h出现的概率为 (13) 设图像阈值为t1,…,tl,…,tn,阈值数目l=1,2,…,n,基于多阈值的类间方差函数的可以定义为 f1(t1,…,tl,…,tn)=w0(μ0-μT)2+…+wk(μk-μT)2+…+wn(μn-μT)2。 (14) (15) 当式(14)中的f1(t1,…,tl,…,tn)取最大值时,即可获得图像的最佳阈值。 假设一幅图像的阈值为t1,t2,则基于两阈值的模糊熵函数可以定义为 f2(t1,t2)=H0+H1+H2。 (16) 式(16)中H0,H1,H2的计算公式分别[24]为 (17) 其中u0(h),u1(h),u2(h)分别表示3个隶属度函数,可以用0≤a1≤b1≤c1≤a2≤b2≤c2的6个参数确定。u0(h),u1(h),u2(h)表达式[23]分别为 (18) (19) (20) 总模糊熵的大小f2(t1,t2)由a1,b1,c1,a2,b2,c2等6个参数确定,利用最大熵准来确定6个参数的最优组合[23],最优分割阈值满足 u0(t1)=u1(t1)=0.5,u1(t2)=u2(t2)=0.5。 (21) 由式(18)、式(19)和式(20)可以得出阈值t1,t2的计算方法[23]分别为 (22) (23) 由两阈值的模糊熵函数的定义公式可以扩展到单阈值和多阈值问题。 为了克服PSO算法在迭代后期易陷入局部最优的缺点,将MVO算法引入到PSO算法中,利用一个可能性参数来控制种群的进化方向。可能性参数Pr计算方法为 Pr=λ+trial(m)/Tmax。 (24) 其中:trial (m)表示当前迭代次数;Tmax表示最大迭代次数;λ是一个动态参数,其取值大小会直接影响种群的进化方向。 随机生成一个数r6∈[0,1],若r6小于Pr,则采用MVO算法进行进化,否则采用PSO算法进行进化。 进化完成后,为了提高算法的精度,在新产生解的周围进行K次混沌搜索,并根据适应度函数的值来判断是否保留搜索到的解。 采用多目标方法进行优化,在进化结束后会获得一组非支配解集。而在实际应用中,只需要一个最优解,因此,需要计算每个非支配解的类间差异和类内紧致的加权比值[24]的最大值作为最优解,加权比值的定义为 (25) 其中:k表示阈值数目;C为图像像素的总数;SA和SE分别表示类间差异性和类内紧致性,其表达式分别为 (26) 其中:Cb为第b类的像素总数;yb表示第b类的灰度平均值;y表示所有像素的平均灰度值;xhb表示第b类中的第h个像素的灰度值。 采用多幅Berkeley图像和互联网脑分割库(the Internet brain segmentation repository, IBSR)的核磁共振(nuclear magnetic resonance, MR)图像进行分割实验,以图像分割准确率、峰值信噪比(peak signal-to-noise ratio, PSNR)、结构相似性(structural similarity, SSIM)作为评价指标,验证算法的性能。 由式(24)可以看出,λ的取值大小会直接影响种群的进化方向,为此对4幅Berkeley图像#3096、#238011、#241004、#42049进行图像分割试验,以确定合适的λ值。当λ分别取0、0.03、0.05、0.08、0.10、0.12、0.20、0.30、0.40、0.50时,4幅图像在不同λ下的分割准确率如图1所示。可以看出λ取0.08时,分割结果最优,因此本算法的λ取0.08。 图1 4幅图像在不同λ下的分割准确率 采用多幅Berkeley图像来验证算法性能。在Berkeley图库选择#3096、#24063、#135069和#241004进行分割,分割结果如图2—图5所示。可以看出CSMHO-PSM算法相对于其他对比算法能够取得更好的分割结果。在图3中,基于多目标粒子群优化[25](multi-objective particle swarm optimization, MOPSO)的阈值图像分割算法和Otsu算法对于右上角的天空和门前的栅栏都存在错分。CSMHO-PSM算法对于天空右上角基本无错分。对于图像#135069,CSMHO-PSM算法相对于Otsu算法明显能够得到更好的分割结果,对比MOPSO算法和基于多目标多元宇宙优化(multi-objective multi-verse optimization, MOMVO)的阈值图像分割算法[21],CSMHO-PSM算法在细节处理方面更为出色,能够更好地保留两只鸟连接处的细节信息。 图2 #3096分割结果 图3 #24063分割结果 图4 #135069分割结果 图5 #241004分割结果 选取10幅Berkeley图像测试不同算法的准确率、PSNR值和SSIM值,共做实验5次,取5次实验的平均值。4种算法的分割准确率、PSNR值和SSIM值如表1所示。可以看出CSMHO-PSM算法相较于其他3种对比算法能够取得更优的分割结果。例如,对于图像#135069,CSMHO-PSM算法的图像分割准确率能达到0.991 7,比Otsu法提高了0.4396,对比PSNR值和SSIM值也分别提高了13.551和0.180 5。在图像#3096中,CSMHO-PSM算法相对于其他对比算法,在图像分割准确率、PSNR值和SSIM上均有所提高。对于多类图像#241004,虽然CSMHO-PSM算法的分割准确率略低于Otsu法,但PSNR值和SSIM值相较于其他3种方法均有所提高。 表1 4种算法对Berkeley图像的分割准确率、PSNR值和SSIM值 为了进一步验证本文算法的实用性,选择更复杂的、来自互联网脑分割库(the Internet brain segmentation repository, IBSR)的MR图像进行分割实验,并用图像分割准确率作为评价标准。不同算法对两幅MR图像的分割结果分别如图6—图7所示。从视觉效果看,本文算法能够取得较为理想的分割结果。由图6中可以看出,本文算法相较于Otsu算法和MOPSO算法能够有效的分清灰质和白质,在视觉效果上有了明显的提升;MOMVO算法虽然能大致分清灰质和白质,但在一些细节处理方面本文算法的性能更优。 图6 切片号12对应的12-3图像分割结果 图7 切片号39对应的16-3图像分割结果 不同算法对MR图像的分割准确率如表2所示。可以看出,本文算法相对于其他对比算法能够取得更好的分割结果。对于切片号7对应的图像2-4,本文提出的CSMHO-PSM算法的准确率为0.967 4,而Otsu算法、MOPSO算法和MOMVO算法的准确率分别为0.953 7、0.941 2和0.955 3;对于切片号8对应的图像8-4,本文算法的准确率为0.967 2,相对于Otsu算法的准确率提升了0.015 3,比MOPSO算法和MOMVO算法的准确率分别高出0.023 2和0.016 5。 表2 4种算法对MR图像的分割准确率 综合不同算法在分割Berkeley图像和MR图像上的各项评价指标和视觉效果上的表现,本文所提出的CSMHO-PSM算法的性能更好,能够得到更优的分割结果。这是因为相对于MOPSO算法,CSMHO-PSM算法引入了MVO算法来改进PSO算法,避免了PSO算法在迭代后期易陷入局部最优的缺点。 针对PSO算法易陷入局部最优,从而导致图像分割效果不稳定的缺点,提出了一种基于粒子群和多元宇宙混合优化的阈值图像分割算法。算法结合了多目标优化,并将类间方差函数和模糊熵函数作为待优化的目标函数。为了进一步避免算法陷入局部最优,在算法中加入混沌搜索策略。仿真实验结果表明,本文算法能够较好地分割图像,相较于Otsu算法、MOPSO算法和MOMVO算法具有更优的分割准确率。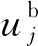
1.3 混沌搜索
2 基于CSMHO-PSM的阈值图像分割
2.1 种群的初始化及编码
2.2 适应度函数的构造
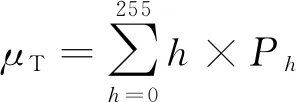
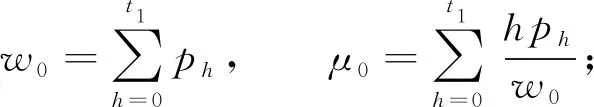
2.3 引入混沌搜索的混合优化策略
2.4 最优解的选择
3 实验结果及分析
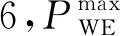
3.1 Berkeley图像分割实验




3.2 MR图像分割实验

4 结语

