两阶段判别嵌入模糊聚类

支晓斌, 牛传林, 李亚兰

(1.西安邮电大学 理学院， 陕西 西安 710121； 2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

聚类[1]是统计多变量分析的方法之一，作为机器学习、模式识别和计算机视觉领域中的一种基本方法，其目的是将相似模式的数据分配到同一个类别中，不同模式的数据分配到不同类别中，并对数据内部结构进行重构。然而，高维数据的复杂性会影响聚类性能，即“维数诅咒”[2]。对高维数据聚类仍然是一个具有挑战性的问题。

判别聚类(discriminative clustering, DC)算法[3]将无监督的聚类方法和有监督的基于线性判别分析(linear discriminant analysis, LDA)[4]的降维方法组合在一个聚类框架中，交替执行初始数据空间中的LDA降维和低维变换空间中的聚类过程，实现了对高维数据的有效聚类，但是，该方法运行效率低。判别K-均值 (discriminativeK-means, DKM) 聚类算法[5]通过消除基于LDA的迭代降维过程，简化了DC算法，但存在小样本问题[6]。判别嵌入式聚类(discriminative embedded clustering, DEC)算法[7]通过交替执行基于子空间学习的降维方法和K-均值聚类方法，利用最大间距准则(maximum margin criterion, MMC)[8]代替DC聚类算法中的LDA方法实现对数据的降维处理，从而避免了LDA面对小样本的问题。但是，DEC算法的计算复杂度高，当数据维数较高时，运行速度慢。为了提高DEC算法的运行效率，改进的判别嵌入式(efficient discriminative clustering, EDEC)算法[9]先利用QR分解[10]实现对样本的初次降维，然后利用MMC对降维后的数据再次降维，通过两次降维，降低了DEC算法的计算复杂度，同时也提高了算法的聚类性能，但该算法对数据适应性较差。为了进一步改善EDEC算法对数据样本适应性差的问题，两阶段判别嵌入式聚类(two-stage discriminative embedded clustering, TSDEC)算法[11]在EDEC算法的基础上对类间散度矩阵正则化处理，即引入正则化参数，使得在保持与EDEC算法相同运行效率的情况下，提高了算法对数据的适应性能力。但是，TSDEC算法中的聚类过程使用的是K-均值 (K-means, KM)聚类算法[12]，本质上是一种硬聚类算法，无法有效地反映数据集的真实分布结构。

在TSDEC算法的基础上，本文提出一种两阶段判别嵌入模糊聚类 (two-stage discriminative embedded fuzzy clustering, TSDEFC)算法。该算法首先通过两阶段降维方法对数据进行处理，降低算法的计算复杂度；其次在初始化和迭代过程中，利用模糊C-均值(fuzzyC-means, FCM)聚类算法[13]实现对数据的聚类，充分考虑每个样本点对数据类中心的影响，以期有效地反映数据的真实分布结构。

1 两阶段判别嵌入式聚类

两阶段判别嵌入式聚类算法在EDEC算法的基础上引入正则化参数λ，通过对类间散度矩阵正则化处理提高算法对数据的适应性[11]。TSDEC算法首先用奇异值分解[14]对正则化处理后的类间散度矩阵进行降维处理，初次降维后的样本数据的维数最大可以降到(c-1)维；然后，在低维嵌入子空间中利用基于最大间距准则的子空间学习方法，对降维后的样本数据再次降维；最后，使用KM算法[12]对两次降维后的样本数据进行聚类。通过两次对样本数据降维处理，降低了算法的计算复杂度，提高了算法的效率。

X={X1,…,Xj,…,Xc}。

其中Xj表示第j类的数据样本矩阵。

聚类的类内紧致性和类间分离性可用类内散度矩阵Sw和类间散度矩阵Sb表示，分别定义[15]为

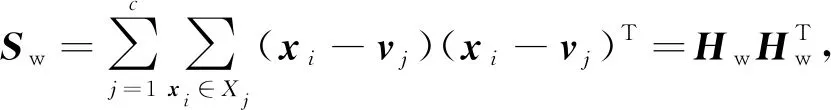
(1)

(2)

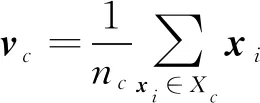
通过对矩阵Hb作奇异值分解得到[14]

Hb=SΣDT。

其中：S∈m×m,D∈m×m,且S和D都是正交矩阵；Σ∈m×c为半正定对角阵。Σ1为Σ的前c行c列构造的矩阵，对其正则化[11]得到

(3)

其中Ic为c阶单位矩阵。

由式(3)可知，矩阵Σ1引入了正则化参数λ，避免了矩阵奇异性问题，从而可以提高算法对数据的适应性。

2 两阶段判别嵌入模糊聚类算法

2.1 初始化聚类和迭代中的FCM算法

KM[12]算法是一种硬聚类算法，得到的是对数据的硬划分矩阵。这种硬划分不能准确地描述数据的分布情况。FCM算法[13]是一种软聚类算法，通过模糊隶属度矩阵确定每个数据样本属于某类类别的确定性程度。在FCM的聚类结果中，每个样本不再属于确定的类别，而是以不同的程度属于各个类别[16]。

FCM算法的目标函数定义[13]为

(4)

其中：矩阵U={uij}n×c为模糊隶属度矩阵；M为样本类中心矩阵；b为控制聚类结果模糊程度的参数，取值大于1；dj表示第j类数据样本的均值；uij∈[0,1]表示数据样本xi属于各个聚类的模糊程度，满足

用目标函数J对dj和uij分别求偏导，并令偏导数为0，可得式(4)最小化的必要条件分别为

(5)

(6)

通过迭代方法求解式(5)和式(6)，得到式(4)的最优目标函数值，具体步骤如下。

输入数据样本X，控制聚类模糊程度的参数b，聚类类别数c，迭代次数以及阈值δ。

输出模糊隶属度矩阵U。

步骤1初始化模糊隶属度矩阵U0。

步骤2根据式(5)计算类中心矩阵M。

步骤3根据式(6)更新隶属度矩阵U，如果满足‖U-U0‖<δ，则停止迭代，得到最优目标函数值；否则，令U0=U，返回步骤2，重复迭代。

2.2 TSDEFC算法原理及其步骤

两阶段判别嵌入模糊聚类算法在TSDEC算法的基础上引入FCM算法，对样本进行初始聚类，得到初始的模糊隶属度矩阵；通过两阶段降维方法[11]对数据进行降维处理；最后在低维嵌入子空间中利用FCM算法对降维后的数据再次进行模糊聚类，得到最终的模糊隶属度矩阵，按照最大隶属度原则确定每个样本点的类别。

TSDEFC算法具体步骤如下。

输入数据样本X，聚类数目c，迭代次数T以及停止阈值ε。

输出隶属度矩阵H。

步骤1对数据样本X进行规范化和中心化处理，并初始化模糊聚类得到模糊隶属度矩阵U0。

步骤2将U0根据隶属度最大化原则构造矩阵H0。

步骤3根据式(2)构造矩阵Hb。

步骤4矩阵Hb作奇异值分解，即

Hb=SΣDT。

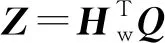
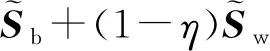
步骤8由G=QW得到最优变换矩阵。

步骤9利用y=GTx对数据进行投影变换，在低维嵌入子空间中使用FCM聚类算法对两次降维后的数据聚类，得到模糊聚类结果并更新模糊隶属度矩阵U。

步骤10根据模糊集合的最大隶属度准则，得到数据的隶属度矩阵H。如果‖H-H0‖<ε，则停止迭代，聚类完成；否则，令H0=H，转到步骤3，直至满足‖H-H0‖<ε为止。

TSDEFC算法是一种软聚类算法，通过计算每个数据点隶属于多个不同类别的模糊程度，充分考虑了每个样本点对聚类中心的影响，从而有效地反映数据集的真实分布结构。

3 实验结果与分析

实验是在Intel (R) Core 2.5 GHz，4 GB 内存的Windows10 系统进行。为了验证TSDEFC聚类算法能够更加有效地反映数据的真实结构，在不同的模糊参数条件下，选取UCI数据库[17]中的Brain、Leukemia、Control、Satimage和Colon 及基因表达数据集Global Cancer Map(GCM)[18]等6个数据集，分别对比TSDEFC算法与TSDEC算法、DEC算法、KM算法以及FCM算法的聚类精度和鲁棒性。6个数据集的相关特性如表1所示。

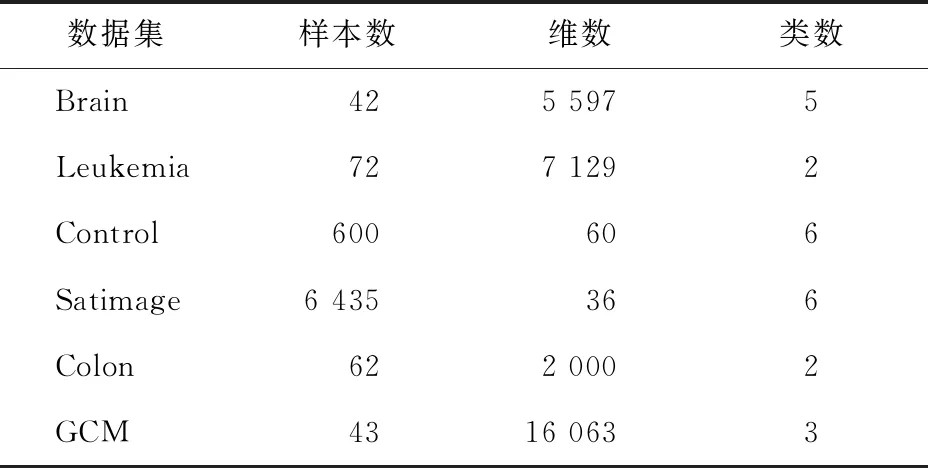
表1 6个数据集的相关特性

3.1 聚类精度测试

6个数据集的平衡参数η取值为2，正则化参数λ取值为10-6。b1表示初始化FCM算法中的模糊参数，b2表示在低维子空间中执行FCM聚类过程的模糊参数。为使实验结果便于分析，令b1=b2，两参数所取值的集合为{1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，2.0，2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9，3.0}。当模糊参数取不同的值时，5种算法运行10次后取其平均值作为最终结果，最大迭代次数设置为100，停止阈值ε设置为10-5。6个数据集的聚类精度的趋势分别如图1至图6所示。

图1 对Brain的聚类结果对比

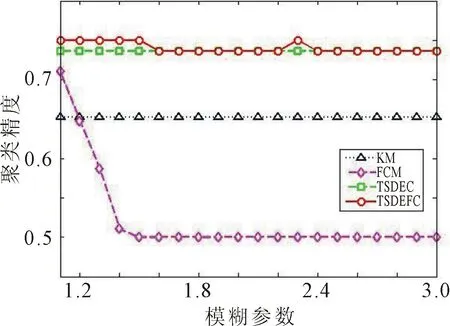
图2 对Leukemia的聚类结果对比 图3 对Control的聚类结果对比

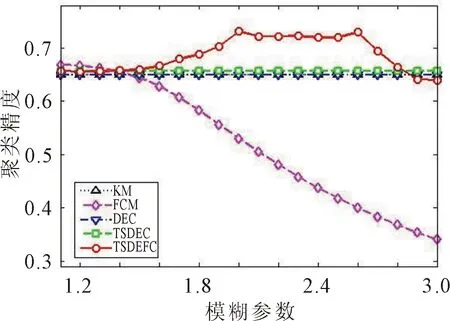
图4 对Satimage的聚类结果对比

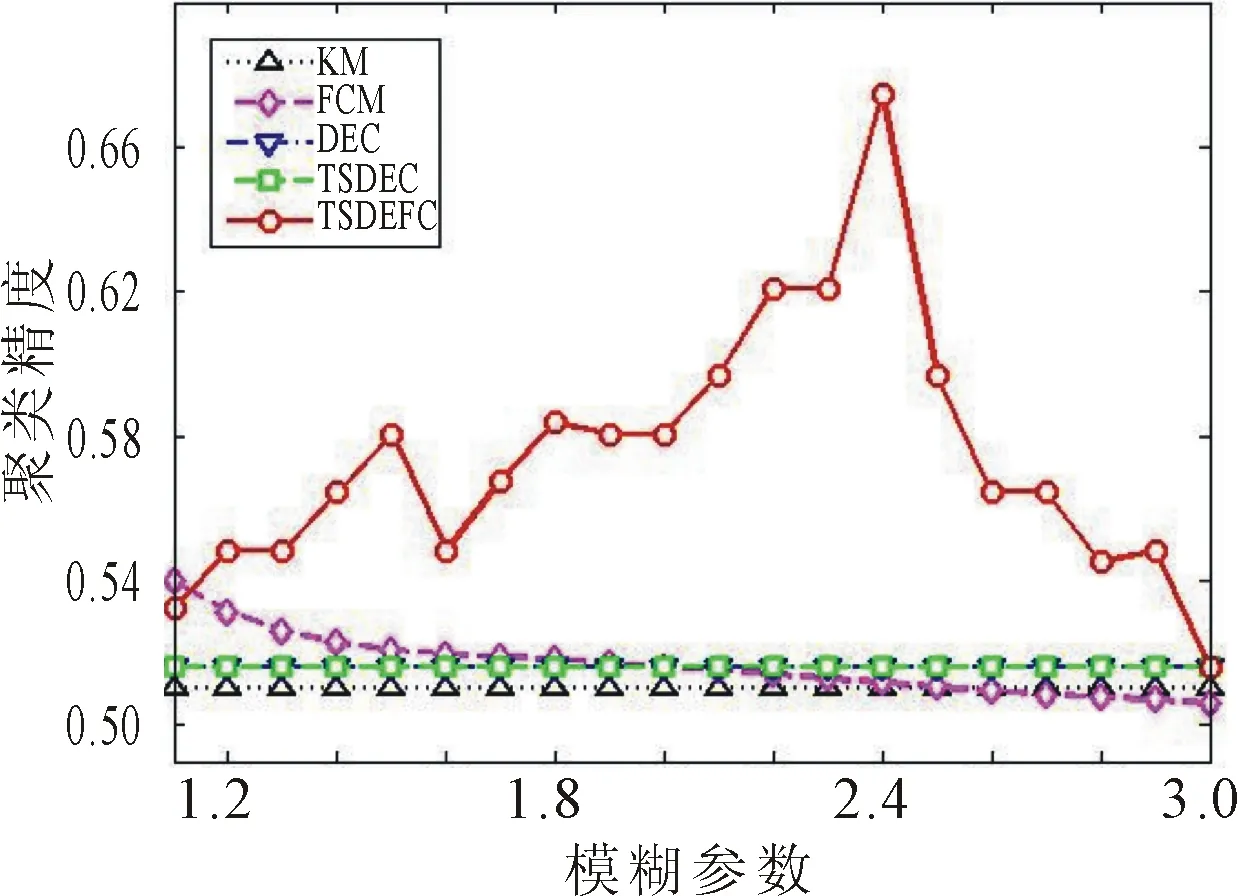
图5 对Colon的聚类结果对比 图6 对GCM的聚类结果对比

由图1至图6的聚类结果可以看出，TSDEC算法、DEC算法和KM算法是硬聚类算法，与模糊参数无关，因此对应的聚类精度是一条直线。而FCM算法和TSDEFC算法的聚类精度随模糊参数的取值的不同而变化。在大多数模糊参数取值下，TSDEFC算法的聚类精度优于其他4种算法，当模糊参数越趋近于1时，聚类精度越接近于TSDEC的聚类精度。

在处理高维数据时，DEC算法在高维数据集Leukemia和GCM上溢出，无法得到聚类精度。从图5和图6可以看出，TSDEFC算法对于数据集Colon和GCM的聚类精度明显优于TSDEC算法、DEC算法和FCM算法。

TSDEFC算法、TSDEC算法、DEC算法、KM算法和FCM算法在不同模糊参数下获得的最优聚类精度如表2所示。其中，“—”表示DEC算法无法得到关于高维数据集Leukemia和GCM的聚类精度。

表2 5种算法对6个数据集的聚类最优精度对比

由表2可以看出， TSDEFC算法的最优聚类精度高于其他4种算法。

3.2 鲁棒性测试

利用GCM和Brain两个高维数据测试TSDEFC算法对数据初始化的鲁棒性。使用KM算法随机初始化10次所得的隶属度矩阵作为FCM算法、DEC算法、TSDEC算法和TSDEFC算法的初始隶属度矩阵。5种算法对GCM和Brain数据集10次运行的结果分别如图7和8所示，其中FCM和TSDEFC中的模糊参数b分别取值2和1.3。DEC算法在对数据集GCM聚类时内存溢出，无法获得最终的聚类精度。

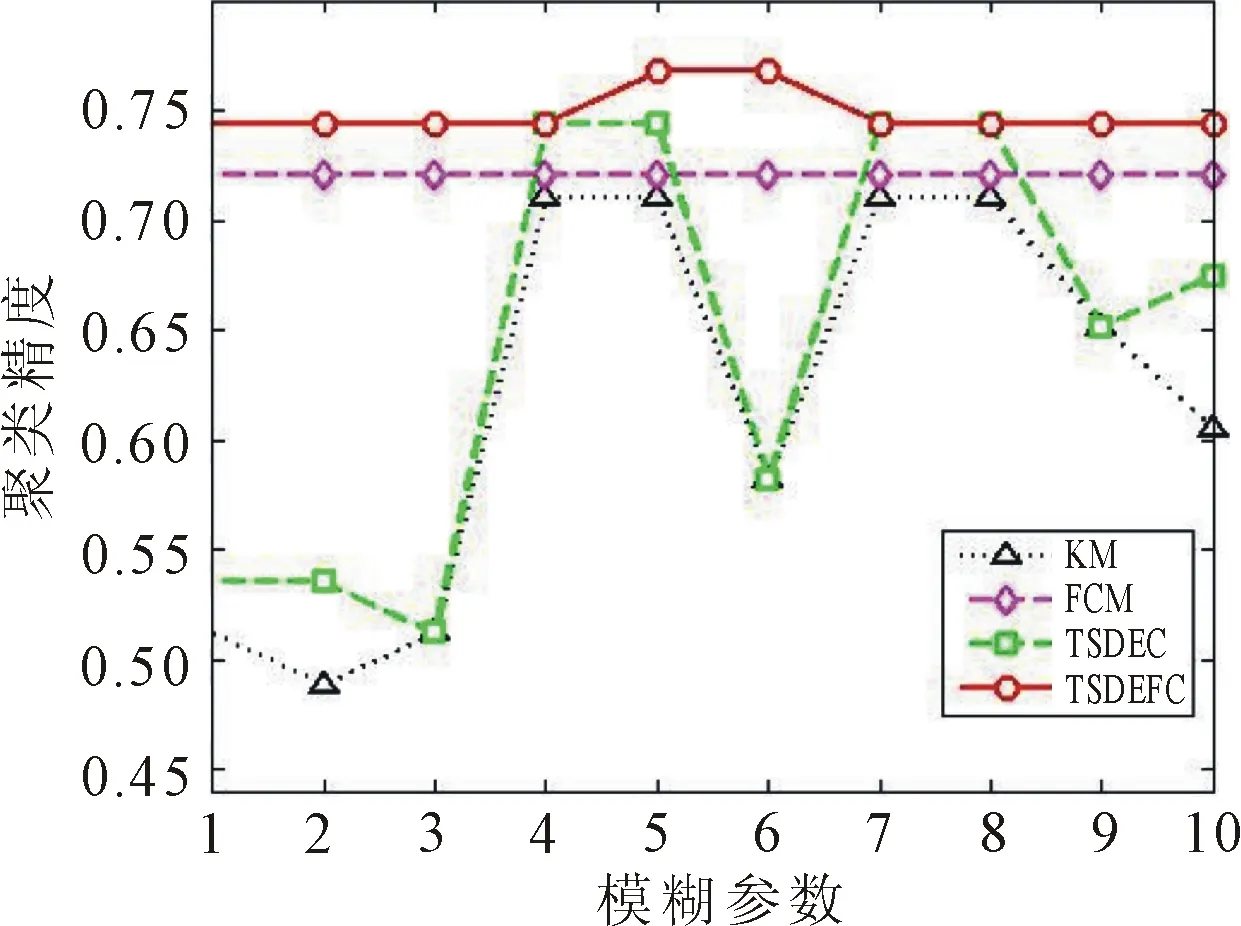
图7 对GCM运行10次的聚类精度对比

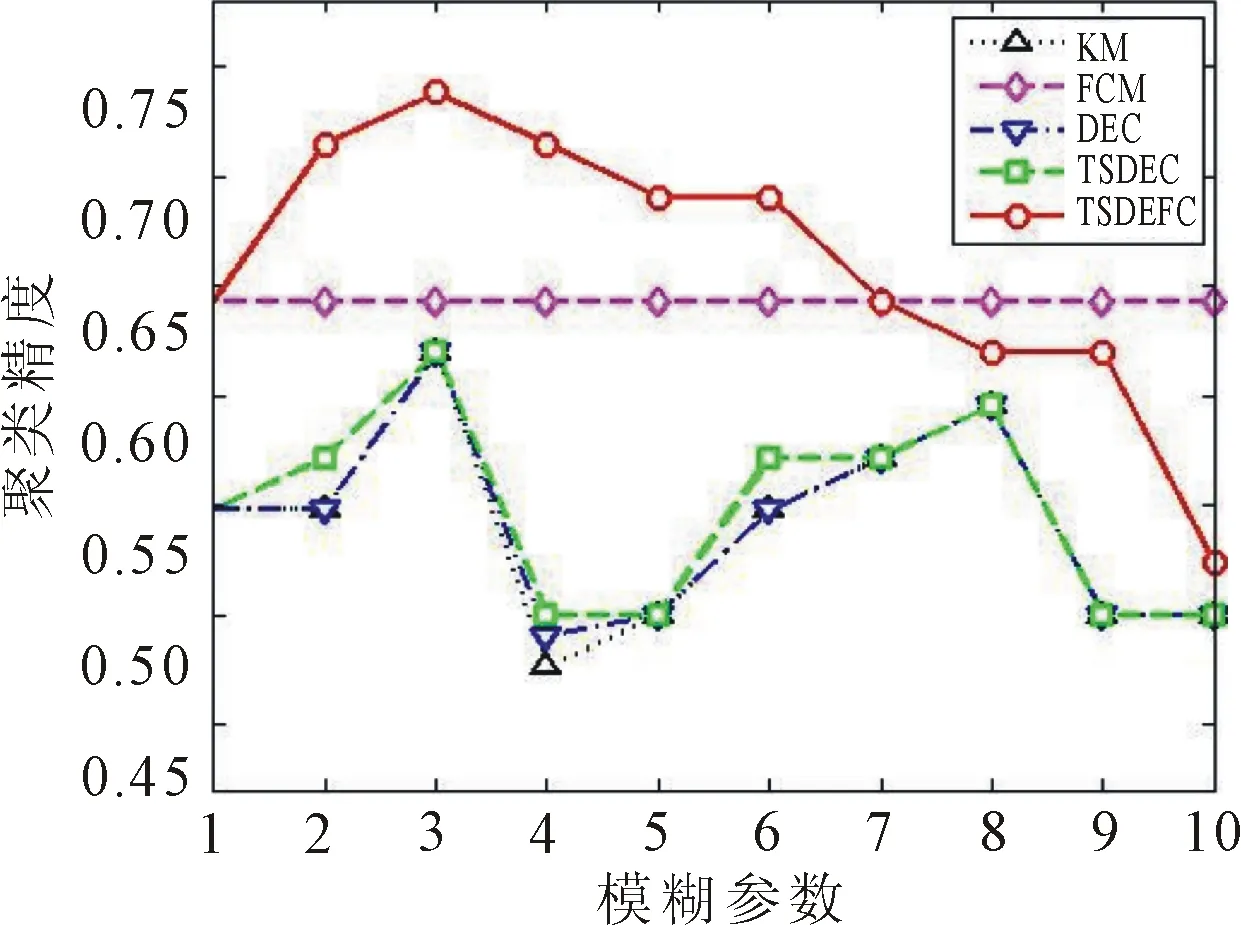
图8 对Brain运行10次的聚类精度对比

由图7和图8的聚类结果可知，对于不同的数据集，TSDEFC算法和FCM算法的聚类精度均超过了KM算法。TSDEFC算法在10次运行中具有比TSDEC算法更优或相同的聚类精度。由于初始隶属度矩阵是随机选择的，表明选取合适的模糊参数，TSDEFC算法相对于TSDEC算法具有更优的对初始化的鲁棒性。

4 结语

TSDEFC算法利用两阶段降维方法对数据降维处理，降低了算法的复杂度。采用FCM算法代替TSDEC算法中的KM算法，对数据模糊化聚类，求得每个数据点属于多个聚类的确定性程度，充分考虑每个数据点对聚类中心的不同贡献。实验结果表明，在多个模糊参数取值下，TSDEFC算法的聚类精度要高于FCM算法，且其聚类精度也优于硬聚类版本的TSDEC算法、DEC算法以及KM算法。尤其对高维数据聚类时，TSDEFC算法的聚类精度优于TSDEC算法、DEC算法及FCM算法，且TSDEFC算法相对于硬聚类版本的算法有更优的对初始化的鲁棒性。