一种灰度直方图与方差修正的图像阈值化算法
张 弘, 张 清, 侯雪梅, 韩凌霏
(西安邮电大学 自动化学院, 陕西 西安 710121)
图像分割是目标提取[1-2]、图像识别[3-4]、图像分析与理解[5]的关键步骤。基于阈值选取的图像分割方法[6-8]通过信息量、灰度均匀性、分割误差和相关性等阈值选取标准对图像进行分割,取得了较好地分割效果。其中Otsu算法以其良好的分割性能、较快地运行速度得到了广泛的应用[9]。然而,对于灰度分布方差差异较大的图像,Otsu算法应用局限性,会出现较大的阈值偏差。
目前,已有的改进Otsu算法是将直方图中各灰度值的高度作为权重,以此调整阈值偏差[10];根据像素及其邻域的灰度分布信息,构造加权函数,修正Otsu算法的类内方差准则,突出波谷对最佳阈值的影响,从而获得更准确的分割阈值[11-12];将背景发生的概率作为Otsu算法分割阈值权重,进而对Otsu算法改进,使得分割阈值更准确[13];文献[14]将目标占整幅图的比例作为加权因子修正类间方差公式,从而改进Otsu算法。然而,上述方法虽然在图像目标与背景方差相差较大时较成功地分割出目标,但是目标在边缘轮廓完整性,以及目标内部细节的保留上存在局限性。文献[15]根据Otsu算法得到阈值的性质,对阈值的选取范围进行优化处理,不仅加快了算法的运行速度,也避免了伪阈值的出现,在一定程度上改善了算法运算效率低问题,但运算量仍然很大。
本文提出一种改进的阈值化算法。基于灰度分布直方图,将灰度概率的邻域信息作为加权函数,对类间方差进行修正,并且基于修正的类间方差与类内方差构造复合函数作为阈值化准则。同时,利用灰度直方图信息对阈值范围进行优化,以此提高算法的运行速度。
1 Otsu阈值准则
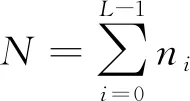
对应的灰度均值[9]分别为
(1)
(2)
其中μ是整幅图像的平均灰度,计算表达式为
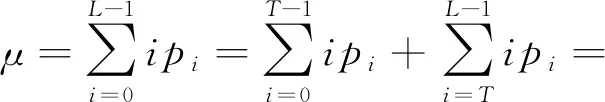
(3)
则Otsu算法的类间方差准则[9]可表示为
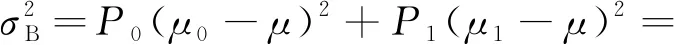
(4)
类内方差准则[9]可表示为
(5)
其中
对应的最佳阈值表示为
(6)
或
(7)
2 改进的阈值化算法
2.1 阈值修正函数的建立
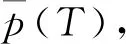
所构造的新准则函数表示为
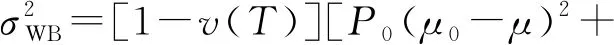
(8)
其中
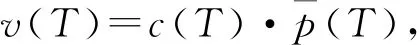
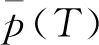
以上准则的建立考虑了灰度分布的形状信息,将波谷与波峰灰度的相对分布概率差作为权重构造准则函数。另外,类内方差也是阈值选择的重要准则,因此,综合考虑类内方差阈值化准则函数,构造最终的阈值准则函数为
(9)
则最佳阈值表示为
(10)
2.2 阈值范围的优化
Otsu算法选取最佳阈值时,对类间方差的计算遍历了整个灰度级范围,即从灰度级为0遍历到灰度级L-1,计算量过大。如果能够减小灰度级遍历的范围,就可以减少算法的执行时间。对于灰度直方图大致呈现双峰形状的图像二值化分割问题,假设将占图像比例小于1/2的区域设为提取目标,图像灰度最小值用α表示,灰度最大值用β表示。若将μ到μ0和μ1的距离分别表示为d0和d1,则
d0=|μ-μ0|,d1=|μ-μ1|。
当目标为低灰度值区域时,有
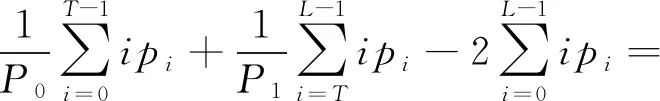
(11)
由式(1)和式(2)可知
将μ0P0和μ1P1代入式(11),可得
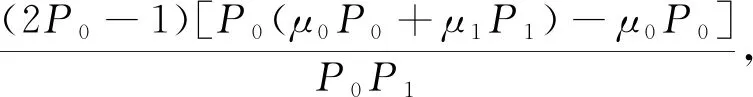
再将式(3)代入上式,化简得到
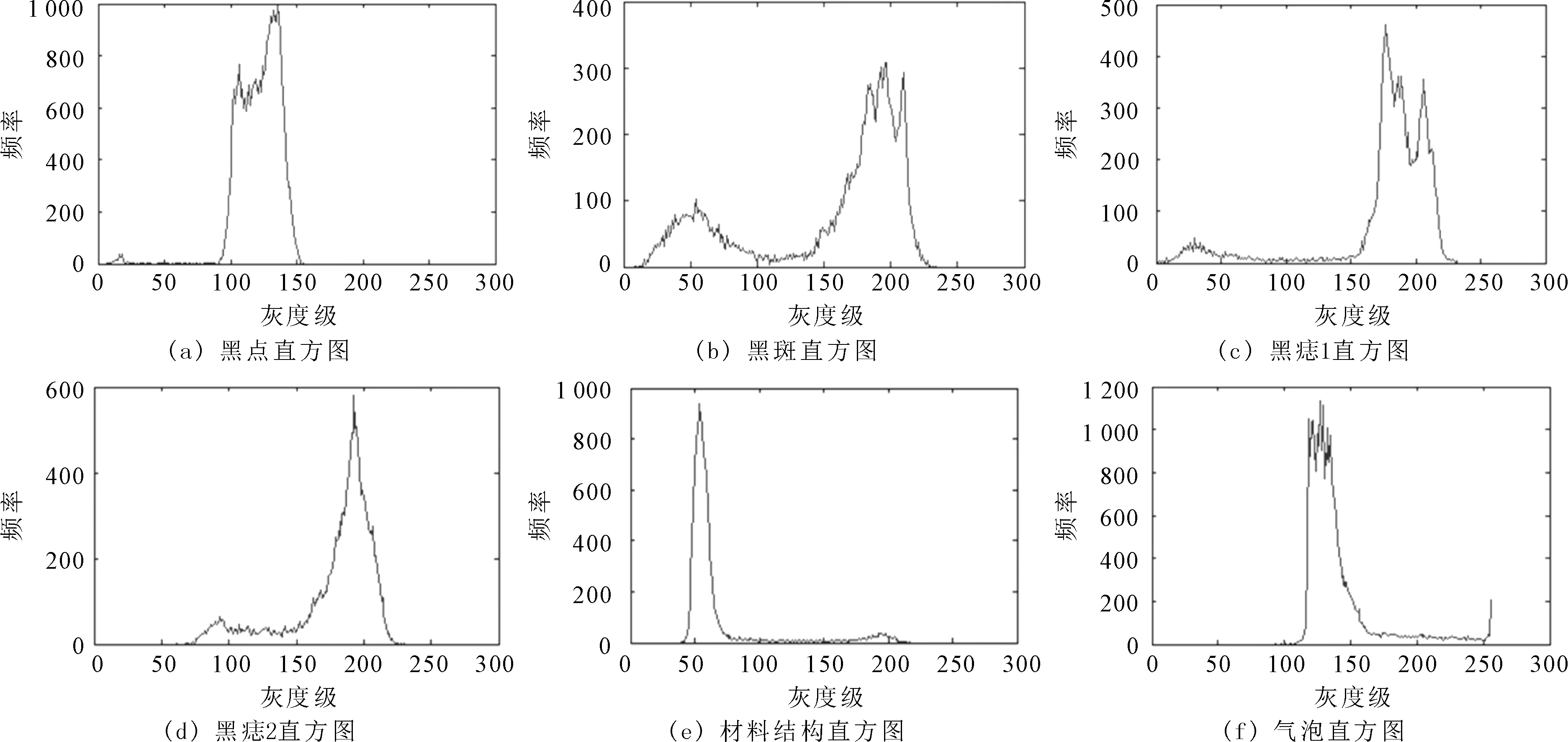
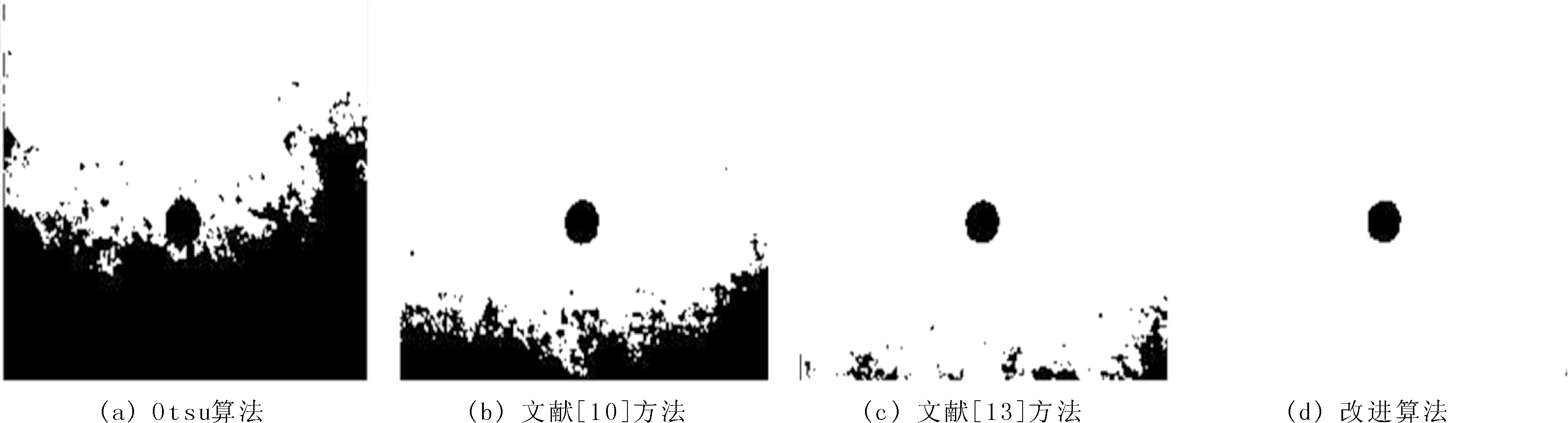
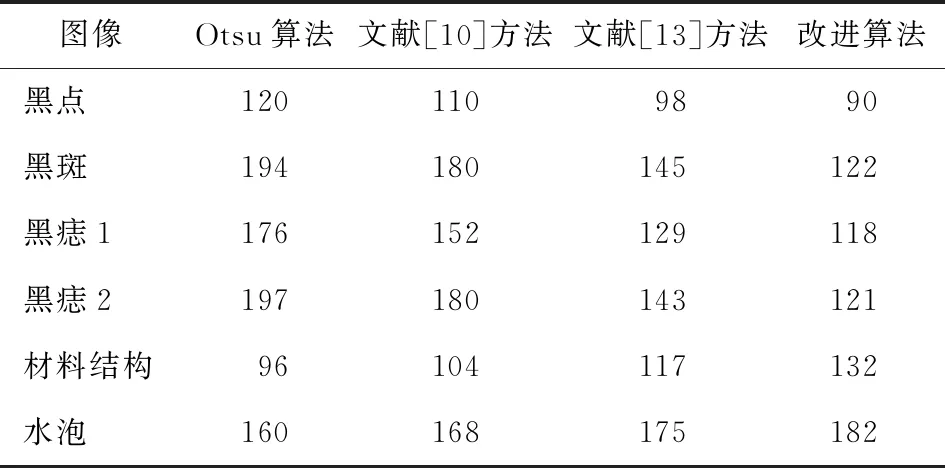
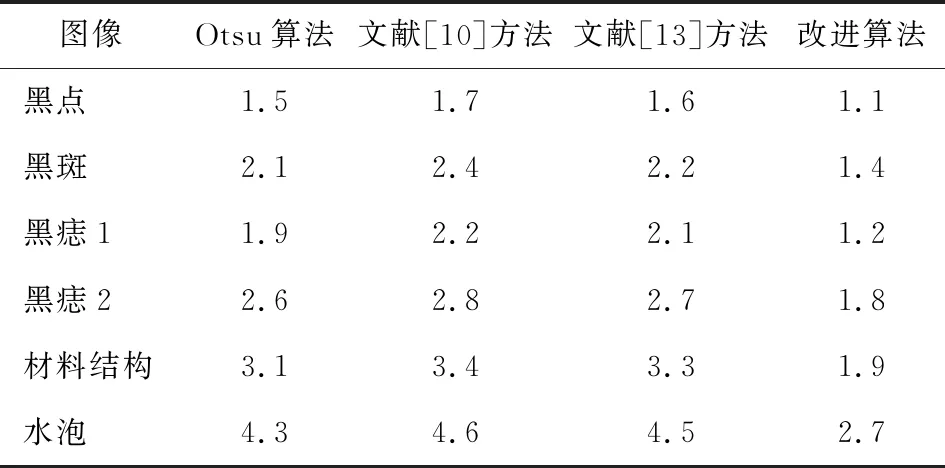
目标部分占整幅图像的比例小于1/2,即P0<1/2,所以2P0-1<0;目标均值小于整幅图像均值,即μ0<μ,所以,μ-μ0>0。综上可知,|μ-μ1|-|μ-μ0|<0,即d1 同理,当目标为高灰度值区域的情况时,有 (12) 将μ0P0和μ1P1代入式(12),可得 再将式(3)代入上式,化简可得 目标占整幅图像的比例小于1/2,即P0<1/2,1-2P0<0;目标在图像中灰度值较高的部分,目标类的均值大于整幅图像的均值,即μ0>μ,μ-μ0<0。因此,|μ-μ1|-|μ-μ0|<0,即d1 对于以上两种情况,最佳阈值范围位于[α,μ]或[μ,β]区域。因此,只需选择[α,μ]或[μ,β]作为最佳阈值的搜索范围,既可减小运算量,又能提高阈值选取的准确性。 根据上述阈值化准则以及阈值范围的优化方法,对直方图呈现双峰的图像进行分割。改进算法的具体步骤如下。 步骤1计算图像的直方图。 步骤2对直方图进行平滑滤波,分别计算μ到两个峰值对应灰度值的距离大小,作为判断目标区域的依据。由于μ更靠近背景区域峰值,设与μ相距大的峰值对应的区域为目标区域。 步骤3比较μ与步骤2中设定的目标区域峰值所对应灰度的大小关系,μ大于峰值灰度则目标是低灰度值区域,否则目标为高灰度值区域。 步骤4如果目标为低灰度值区域,则根据图像直方图得到最小灰度值α,转向步骤5;如果目标为高灰度值区域,那么根据图像直方图得到最大灰度值β,转向步骤6。 步骤5令T的初始值为α,根据改进的最佳阈值选取准则式(10),遍历灰度级范围为[α,μ],转向步骤7。 步骤6令T的初始值为μ,根据改进的最佳阈值选取准则式(10),遍历灰度级范围为[μ,β],转向步骤7。 步骤7获取使函数取得极大值时的T即为最佳阈值。 步骤8根据最佳阈值T进行图像分割。 实验在Intel Core 2.50 GHz CPU、4 G memory以及Matlab 2013 b环境下进行。选取黑点、黑斑、黑痣1、黑痣2、材料结构及气泡等6幅有代表性的图像进行分割实验,分别对比改进算法与Otsu算法、文献[10]方法、文献[13]方法的分割结果。6幅图像的大小分别为214×159、131×131、132×128、132×130、202×68及175×166。每张图像的原图如图1所示,对应的一维灰度直方图如图2所示,实验分割结果分别如图3至图8所示。 图1 原图像 图2 图像对应的一维直方图 从图2直方图可以看出,6幅图的目标与背景灰度分布方差有较大差异,其中图2 (a)至图2 (d)是目标为低灰度值区域的图像,图2 (e)和图2 (f)是目标为高值区域的图像。 图3 黑点图分割结果 图4 黑斑图分割结果 图5 黑痣1图分割结果 图6 黑痣2图分割结果 图7 材料结构图分割结果 图8 气泡图分割结果 由图3—图6分割结果可观察到,当目标为低灰度值区域时,Otsu算法有较大的错分区域,目标边缘模糊不清,分割效果较差;文献[10]和文献[13]方法基本能得到目标轮廓,分割效果有所改善,但是分割出的目标边缘不够清晰、错分点依旧很多;改进算法能将目标从背景中正确提取出来,同时目标轮廓完整、边缘清晰,在4种方法中分割效果最好。 由图7和图8分割结果可以看出,当目标为高灰度值区域时,Otsu算法能较成功的分割出目标,但是依然存在少量的错分点,目标内部细节信息的保留效果欠佳;文献[10]和文献[13]方法的分割结果比Otsu算法的错分点减少,所提取的目标轮廓更完整,但是目标内部的纹理细节信息依旧有待改善;改进算法在正确分割目标的同时,对目标外部轮廓以及内部纹理等信息提取依然能保持最佳。 4种方法获得的阈值结果如表1所示,选取最佳阈值用时如表2所示。 表1 4种方法的阈值结果 从图2直方图可以看出,最佳阈值位于目标峰和背景峰之间的波谷处。由表1可知,当目标处于低灰度区域时,Otsu算法获得的阈值偏大,文献[10]和文献[13]方法所得到的阈值比Otsu算法小,但是依旧存在偏差;当目标处于高灰度区域时,Otsu算法得到的阈值偏小,文献[10]和文献[13]方法比Otsu算法获得的阈值更加准确,但是仍然存在误差。而改进算法在两类区域得到的阈值均比其他方法准确。 表2 4种方法阈值化运行时间/ms 由表2可以看出,文献[10]方法阈值选取运行时间最长,文献[13]方法与Otsu算法相比耗时更短,但是两者均比文献[10] 耗时较短。改进算法相比其他3种方法,缩短了阈值选取的范围,所用时间达到最短,尤其是在材料结构和水泡两幅图像的处理上速度优势明显。 利用改进的阈值化算法对目标与背景方差相差较大的图像进行分割时,获得的阈值更加准确,从而使得分割效果良好。实验结果表明,改进的阈值化算法所提取的目标轮廓更完整,纹理更清晰,且算法的运行时间最短。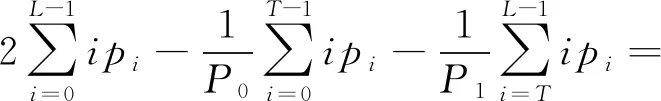
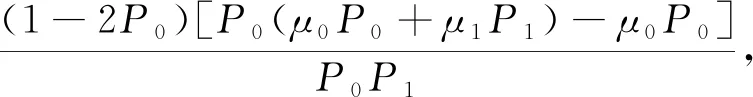
2.3 改进算法的步骤
3 实验结果及分析






4 结语

