改进的卡尔曼滤波的铷原子钟钟差预测

张继荣, 汤利娜

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

钟差预测[1]是原子钟运行状态预测以及原子钟系统驾驭精度提高的关键。根据原子钟的历史钟差数据，可通过钟差预测对原子钟下一刻的钟差进行估计。但是，原子钟受自身特性和环境噪声的影响，会产生瞬时变化，进而影响其同步性能。目前，铷原子钟因其相对便宜的价格优势，已广泛应用在实际工程中。

常用的钟差预测算法包括一次线性回归算法[2]、人工神经网络算法[3]、二次项模型[4]和支持向量机(support vector machine，SVM)[5]。一次线性回归法虽然简洁易实现，但估计精度低。人工神经网络算法具有记忆不稳定、学习速度慢等缺点，使用不当会导致预测结果与真实结果背离[6]。二次项模型简单易实现，能得到变化趋势，但精度不高[7]。SVM的精度高，但是主要依赖于SVM核函数和参量的选择，钟差序列为非平稳的序列，固定的核函数和参数无法满足不同的频率分量[8-9]。

卡尔曼(Kalman)滤波[10]算法具有较高的鲁棒性，基于Hadamard方差的卡尔曼滤波模型对铷原子钟进行钟差预报时，测精度较高[11]。但是环境的干扰导致卡尔曼滤波算法会出现滤波发散的问题[12]。因此，针对Kalman滤波的发散问题，本文提出一种改进的卡尔曼滤波算法。通过加入SVM的惩罚措施和幅值限制，调整铷原子钟的调整参数，对铷原子钟状态进行估计，从而减小因钟差跳变对铷原子钟同步信号的影响。

1 钟差特性

采用全球定位系统(global positioning system，GPS)接收机输出的秒脉冲信号为标准参考源，得到铷原子钟及其钟差，根据钟差值估计铷原子钟的调整参数，最终实现对铷原子钟的控制。

铷原子钟的噪声包括白色调相噪声、闪变相位噪声、白色频率噪声、闪变调频噪声和随机游走频率噪声[13-14]。铷原子钟与标准参考源之间的差规律[11]为

(1)

其中a，b，c分别为铷原子钟的调整参数。a为起始铷原子钟与标准参考时源的钟差；b为起始铷原子钟的频率与标准参考频率的差；c为老化率，由铷原子钟本身性质变化决定[11]，ξ(t)为噪声部分，t为时间。

2 Kalman滤波算法钟差预测

卡尔曼滤波算法采用递归方法，在每步进行递归运算时，只需考虑前一时刻输入信号即可。因此，提高前一刻状态估计精度，便能提高卡尔曼滤波算法的钟差预测精度。

在进行铷原子钟钟差预测时，第i次采样的状态向量由调整参数a，b，c构成，表达式为

xi=[a(i),b(i),c(i)]T。

第i-1次采样到第i次采样的状态向量迭代表达式[11]为

xi=Axi-1+qi-1。

(2)

其中:A为系统传输矩阵，是常数阵，与采样间隔有关；qi-1为三维噪声，服从均值为零的正态分布，时间上互不相关。

第i次采样的钟差测量值[11]为

yi=Hxi+ri。

(3)

其中：H=[1,0,0]为量测矩阵；ri为一维白噪声。

第i次采样后，状态向量xi的先验误差方差阵为

(4)

其中：Pi-1为前一刻后验误差方差阵；Q为状态噪声的方差阵。

状态向量xi的先验估计值为

(5)

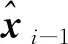
(6)

更新误差方差阵为

(7)

用于下一时刻先验误差方阵的计算，其中I为单位矩阵。

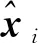
3 改进的Kalman 滤波算法钟差预测

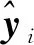
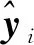
2) 加入幅值限制，改善钟差预测可能出现较大跳变影响下级时钟的同步跟踪问题，提高估计精度。

4 实验结果及分析

选取中国科学院国家授时中心提供的两组钟差数据作为实验数据，分别利用Kalman滤波算法和改进的Kalman滤波算法进行钟差预测。第1组数据为2018年7月29日0时到2018年7月30日0时的数据，共有288个数据点；第2组数据为2018年8月31日0时到2018年9月1日0时的数据，共288个数据点。以每组数据的前50个钟差数据作为训练集，后238个钟差数据为比对数据进行预测。

4.1 两种算法的钟差预测结果

第1组钟差数据的Kalman滤波算法和改进的Kalman滤波算法的钟差预测结果如图1所示。相对预测误差为钟差的测量值和预测值的差与测量值的比值的绝对值，两种算法的预测相对误差如图2 所示。

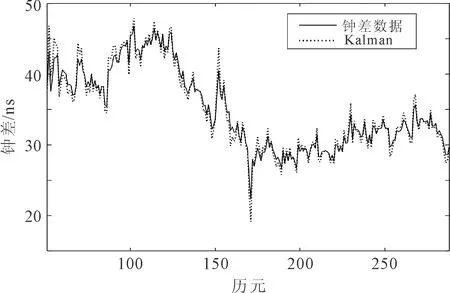
(a) Kalman滤波算法的钟差预测结果

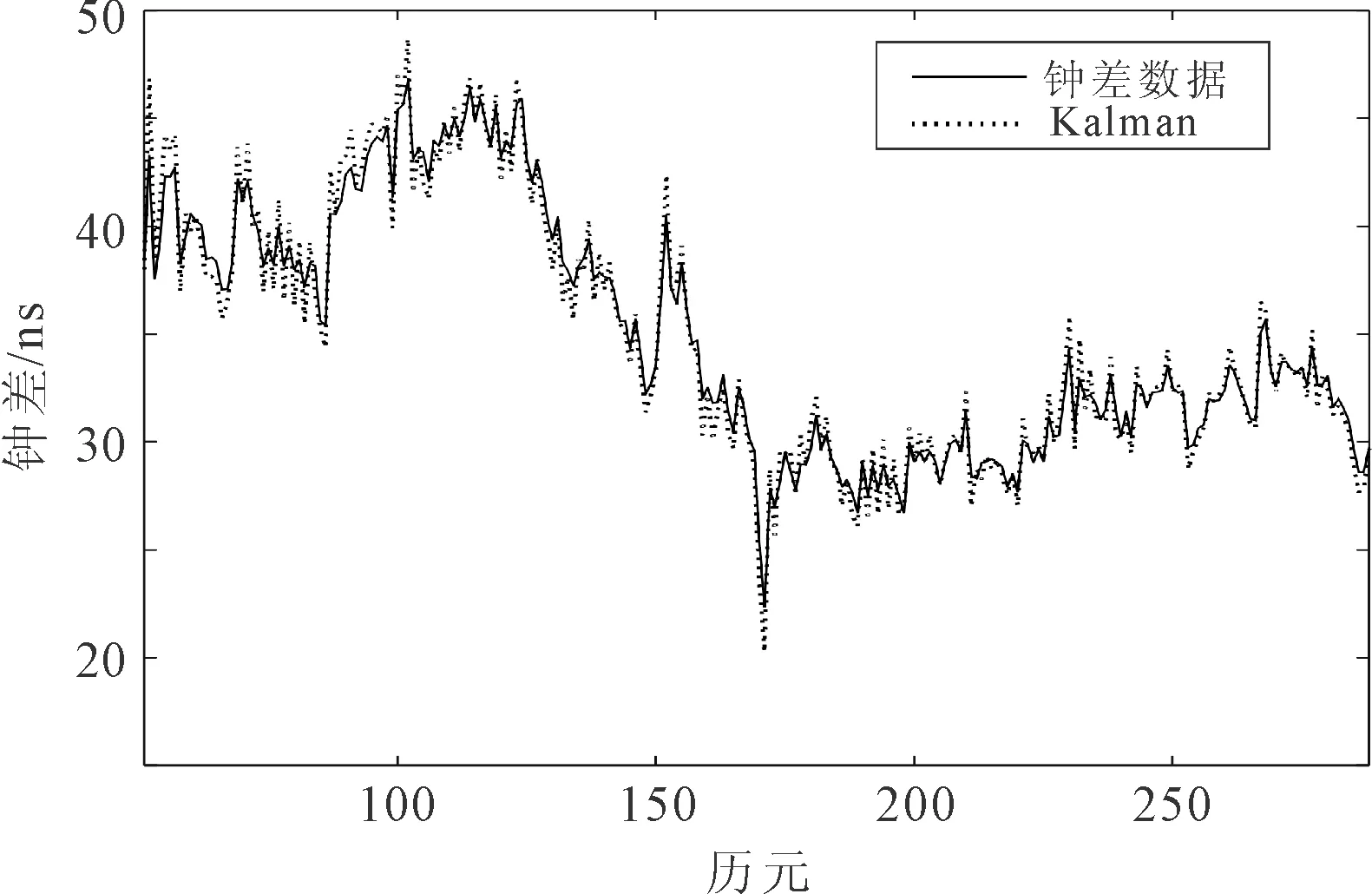
(b) 改进的Kalman滤波算法的钟差预测结果

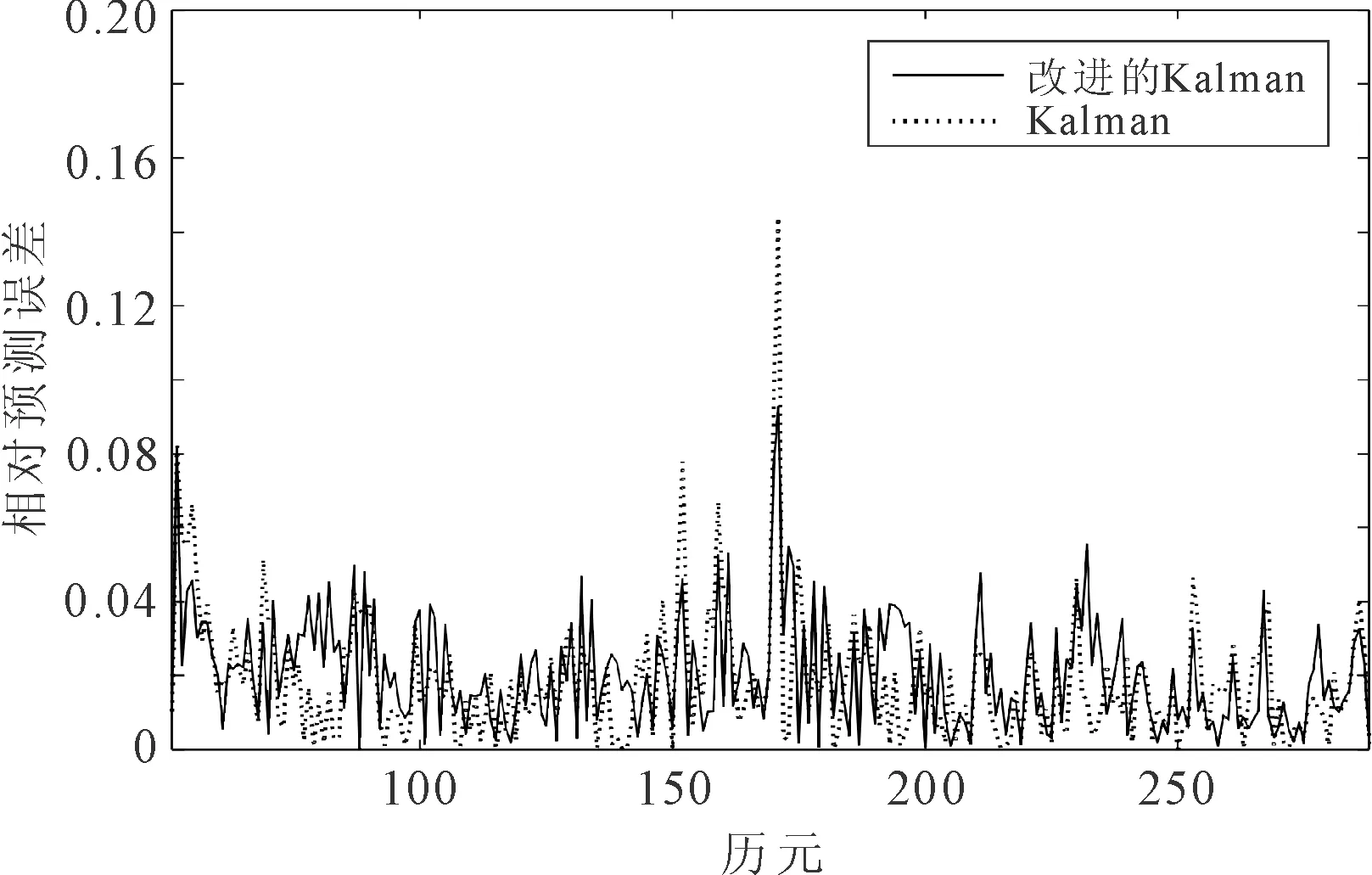
图2 两种算法第1组钟差数据的预测相对误差

第2组钟差数据的Kalman滤波算法和改进的Kalman 滤波算法的预测结果如图3所示。相对预测误差如图4所示。

(a) Kalman滤波算法的钟差预测结果

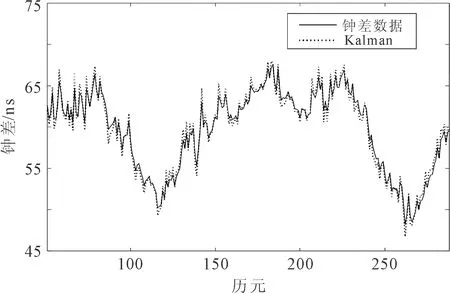
(b) 改进的Kalman滤波算法的钟差预测结果

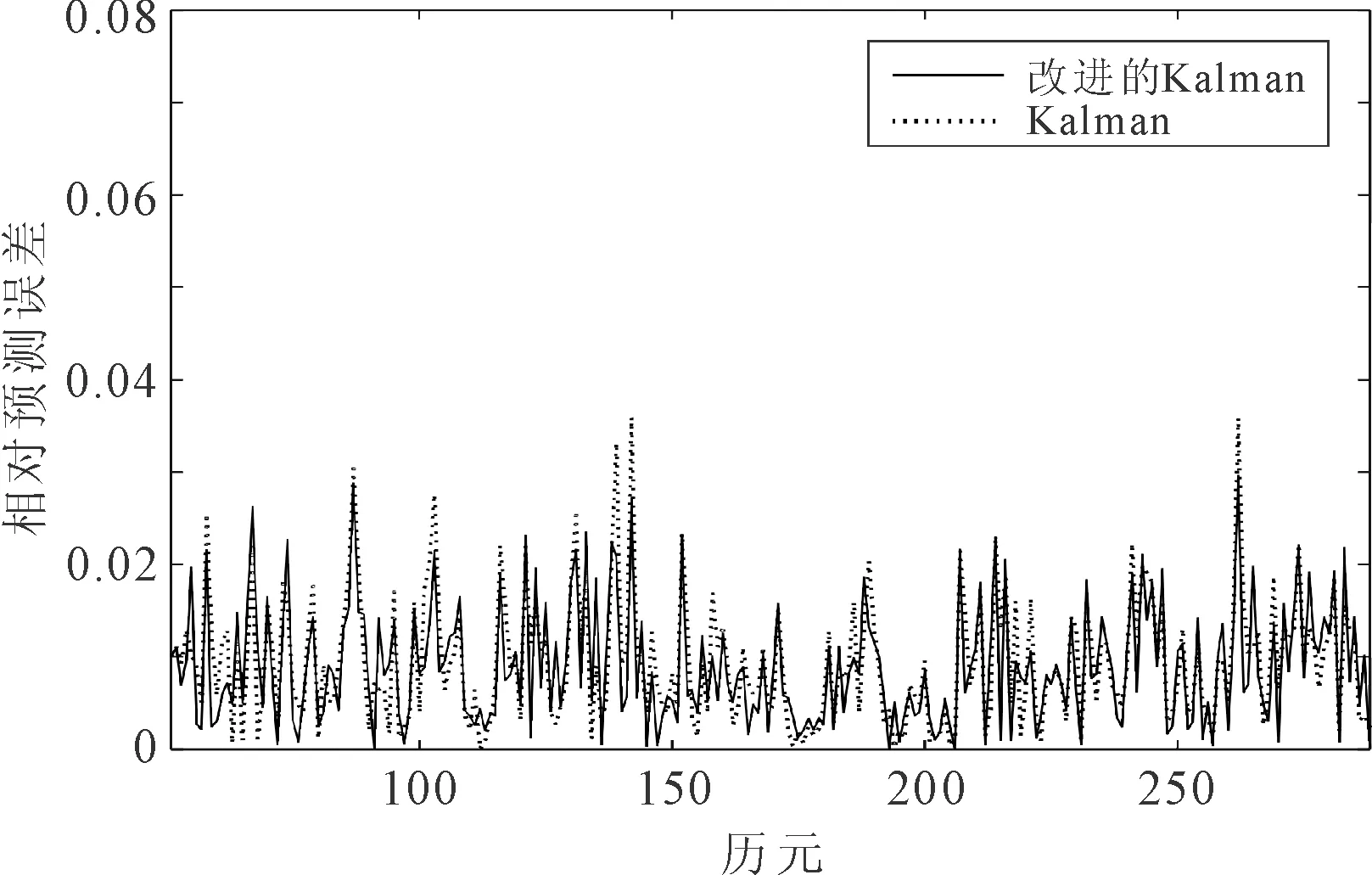
图4 两种算法第2组钟差数据的预测相对误差

由图1、图2、图3和图4分别可以看出，Kalman滤波算法和改进的Kalman滤波算法都可以实现对铷原子钟钟差数据的变化趋势跟踪。但是，在钟差出现较大波动时，Kalman滤波算法的预测误差较大，而改进的Kalman滤波算法的预测误差相对减小。Kalman滤波算法的预测误差方差为0.718，改进的Kalman滤波算法为0.565。与Kalman滤波算法相比，改进的Kalman滤波算法的预测精度有明显提高。

4.2 系统参数对预测结果的影响

1) 惩罚系数影响

通过改变惩罚系数的值，同时保持其他参数值不变，获得与每个惩罚系数相对应的平均相对预测误差，进而对惩罚系数对估计精度产生的影响进行分析，结果如图5所示。

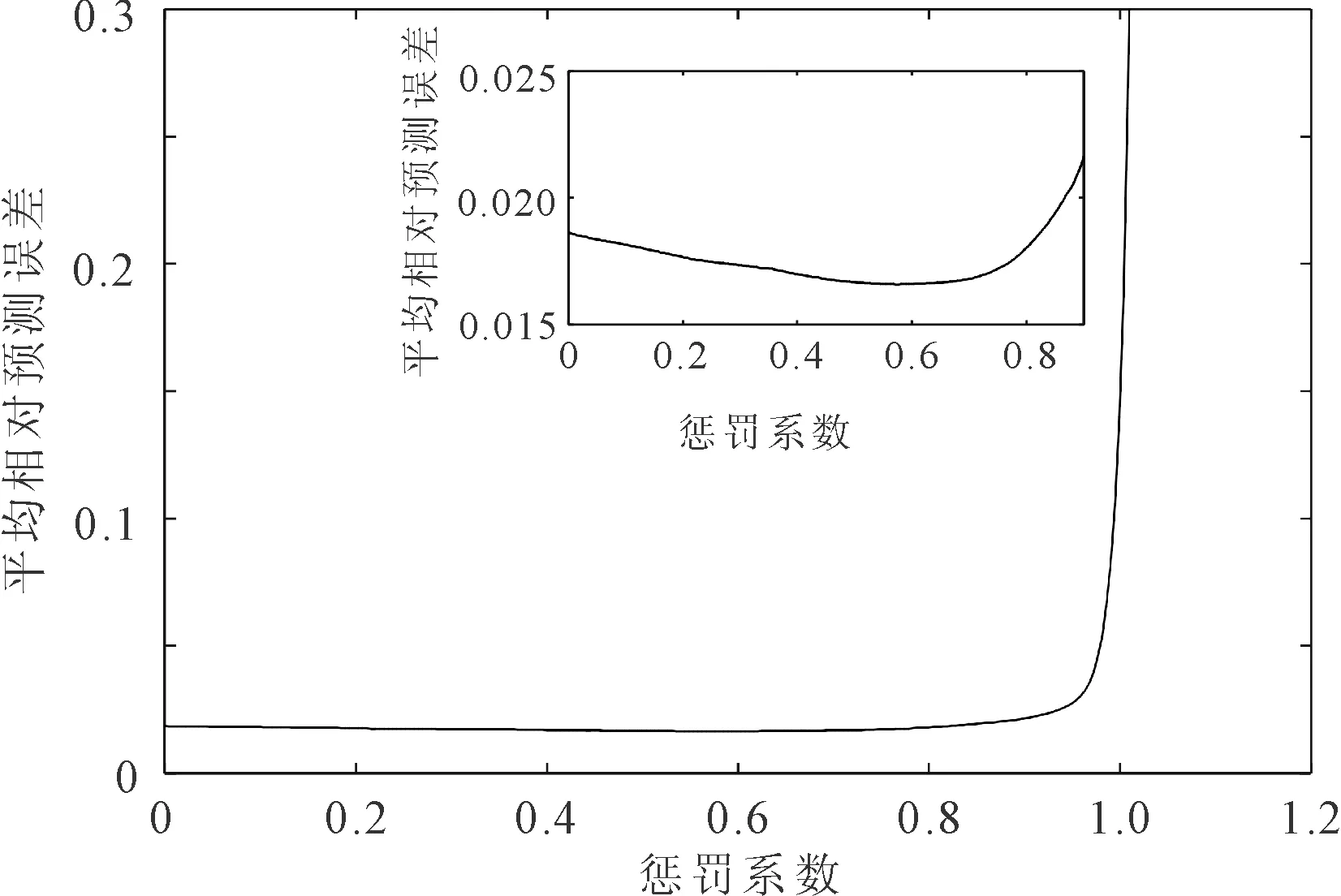
图5 惩罚系数对预测误差的影响结果

对惩罚系数处于0～0.9范围内的预测误差进行分析，可以看出，当惩罚系数接近0时，平均相对预测误差较大；当其处于0.4～0.65范围内时，平均相对预测误差相对较小；当惩罚系数接近1时，平均相对预测误差会随着惩罚系数的增大而骤然增大。因此，适当的惩罚系数对算法平均相对预测误差的减小起促进作用，进而提升估计精度。

2) 幅值限制影响

对限制幅度值进行改变，同时保持其他参数值不变，得到与每个限制幅度值对应的平均相对预测误差，进而分析限制幅度值对预测精度的影响，结果如图6所示。

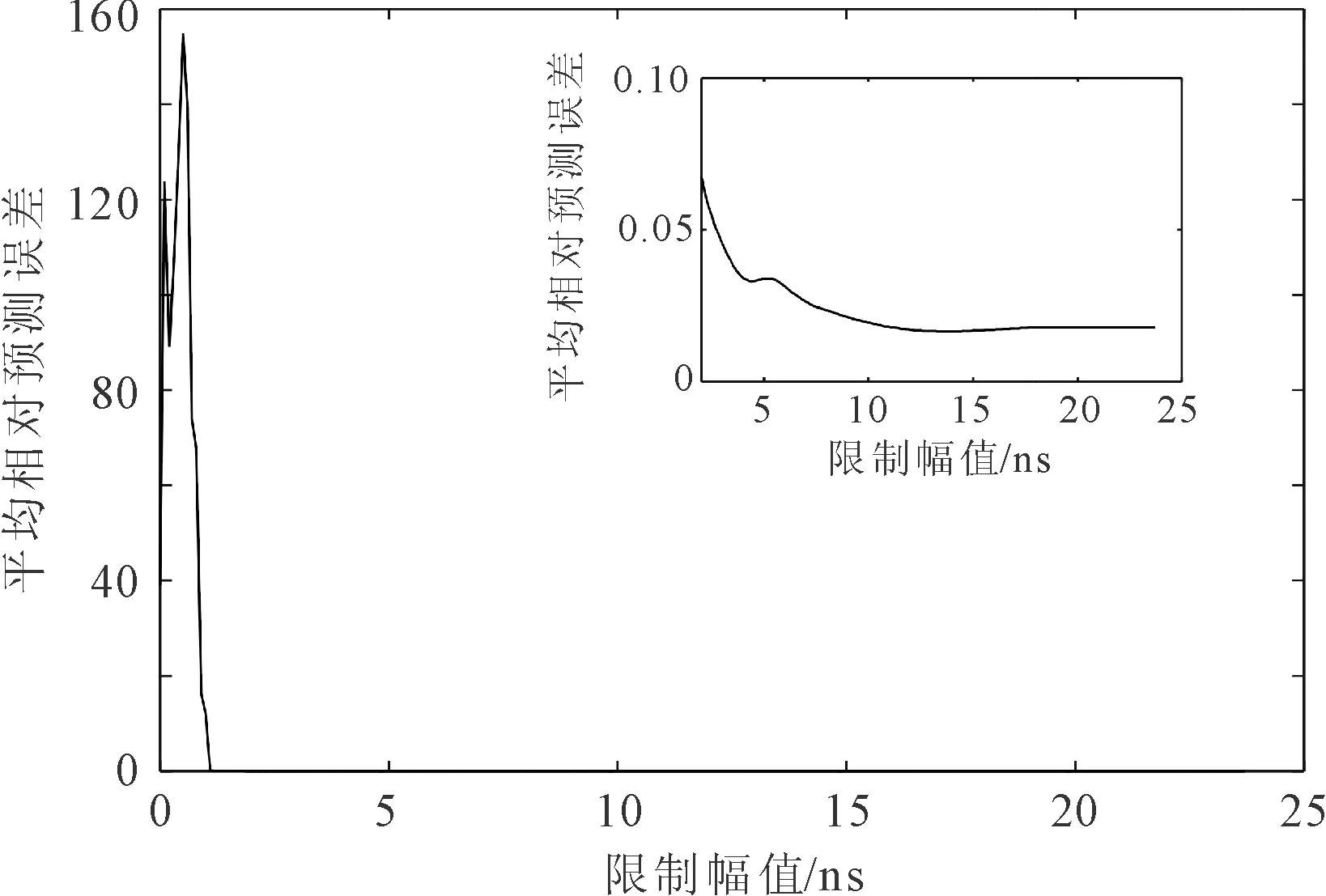
图6 幅值限制对预测误差的影响结果

从图6可知，当限制幅度小于5时，平均相对预测误差较大。当幅度值处于2～30范围内，随着限制幅度的扩大，平均相对预测误差降低。当限制幅度值处于10～15范围内，平均相对预测误差达到最小；当限制幅度小于2时，会限制算法的正常预测，从而使平均相对预测误差较大；限制幅度过大时，导致算法异常值的预测失去限制作用。因此，选择适当的限制幅值，限制对系统异常跳变值的估计，从而降低了系统平均相对预测误差，提升了铷原子钟的估计精度。

从上述实验结果可以看出，改进的Kalman滤波算法与Kalman滤波算法相比，能明显提高预测精度，且合适的参数选取对算法预测精度的提高有促进作用。

5 结语

改进的Kalman滤波算法，通过加入预测惩罚和幅值限制等措施对铷原子钟钟差进行预测，提高了钟差预测精度，且改善了Kalman滤波算法在钟差数据存在较大跳变时产生较大预测误差的问题。实验结果表明，改进的Kalman滤波算法与Kalman滤波算法相比，能明显提高预测精度，且合适的参数选取对算法预测精度的提高有促进作用。