基于对偶犹豫模糊语言的多属性决策方法
汪永玲,冯向前,张华荣
(南京师范大学a.计算机科学与技术学院;b.科技处,南京 210023)
0 引言
多属性决策作为现代决策科学的重要组成部分,对不同方案根据多个有影响的属性做出评价,以选择理想的备选方案。同时由于决策环境的不确定性日益突出以及决策者关于决策问题领域的知识或数据的缺乏,因此决策者在评价过程中很难用明确的数字或确定的语言术语来表达决策偏好,从而产生了相应的模糊语言多属性决策。模糊语言多属性决策作为决策科学领域的研究热点之一,该方面的研究近年来也取得了丰硕的成果。Zadeh[1]于1965年提出模糊集理论,将现代社会中各领域的研究范畴从精确化扩展到模糊化,用隶属度来刻画模糊集中元素的模糊性。为了更加详细的描述模糊信息,Atanassov[2]于1986年提出了直觉模糊集的概念,他在模糊集中同时考虑到隶属度、非隶属及不确定信息,从而更加细腻的描述了客观世界的模糊性。Zhu和Xu[3]等于2012年提出对偶犹豫模糊集,它的隶属度和非隶属度均由[0,1]之间多个可能的数值组成,因此对偶犹豫模糊集表现出更强的模糊信息处理能力。这种新的处理模糊性的工具的提出很快引起了学者的广泛关注并得到了迅速发展。Su和Xu等[4]对对偶犹豫模糊集的距离测度和相似度度量进行了研究并将其运用于模式识别。Pushpinder[5]也对其距离测度和相似度度量进行了研究并将其运用于多属性决策中。Ren和Xu等[6]开发了基于对偶犹豫模糊元的得分函数、比较方法和距离度量,基于此扩展了VIKOR方法以解决多属性群决策问题。
在多属性决策过程中,由于决策环境的复杂性,因此决策者更喜欢用模糊语言信息来表述对决策对象的评价,诸如“好”、“一般”“差”等。但是单纯的语言表述也不能很好的刻画客观评价的模糊性,因此,王坚强等[7]提出直觉语言集的定义、运算法则、期望值、得分函数,精确函数以及直觉语言加权平均算子和集合平均算子。Yang和Ju[8]在基于语言信息和对偶犹豫模糊集的基础上于2014年提出了对偶犹豫模糊语言,给出相应的运算法则,得分函数以及集结算子。本文提出了对偶犹豫模糊语言的距离公式和新的得分函数及方差函数,并考虑在决策过程中属性权重未知的情况下,运用熵权和方差权的组合权重法并结合经典的TOPSIS决策法给出一种对偶犹豫模糊语言的多属性决策排序方法。
1 基础知识
定义1[9]:设表示为一个有限离散语言的集合,且对任意的si,sj∈S满足下列条件:
(1)若i>j,则si>sj;
(2)存在负算子:neg(si)=sj,使得i+j=o;
(3)若si≤sj,则 min(si,sj)=si;
(4)若si≥sj,则 max(si,sj)=si。
定义 2[11]:设为一个特定的集合,则直觉语言集可以描述为如下的形式:

其中,sθ(xi)∈S(S为语言术语集);μ(xi)表示xi隶属于sθ(xi)的程度,ν(xi)表示xi非隶属于sθ(xi)的程度,是由区间上的数构成,且-ν(xi)表示xi属于sθ(xi)的犹豫程度。为了方便,称三元组为一个直觉语言数。例如
定义 3[11]:设和为任意的两个直觉语言数,则I1和I2之间的距离可以表示为以下形式:

最常用的直觉语言的得分函数是由Liu和Wang[11]提出的但是该得分函数存在一定的局限性。如:当τ=6时,的大小比较过程中,因此I1<I2。但是这显然与人类的直觉不同,I1中的不赞同率只比赞成率小0.05,I2中的赞同率只比不赞成率多0.05,而其语言术语s6是远远大于s1的,因此,就直觉来说,应该是I1>I2。针对这样的局限性,本文提出新颖的直觉语言得分函数。因直觉语言数与的得分函数一方面受已知信息即语言术语值θ及隶属度μ和非隶属度ν的影响,这一方面可用该对象到拥有相同语言术语值θ的负理想点的海明距离来衡量;另一方面还会受到该对象的缺失信息即犹豫度的影响,这一方面可用该对象的确定程度即μ+ν来表示。最终可得直觉语言数的得分函数为:
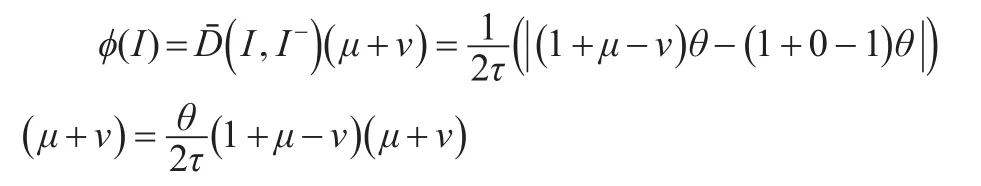

针对上述例子:当τ=6时,与的大小比较问题,按定义3可得ϕ(I1)=0.451,ϕ(I2)=0.158。所以I1>I2,这是符合人类的主观直觉的。由此可见,新的得分函数更能帮助解决直觉语言的大小比较问题。
2 对偶犹豫模糊语言
2.1 对偶犹豫模糊语言数的基本概念
定义5[8]:设X={x1,x2,...,xn} 为一个特定的集合,则对偶犹豫模糊语言集可以描述为如下的形式:

其中,sθ(xi)∈S(S为语言术语集);h(xi)和g(xi)分别表示xi隶属于和非隶属于sθ(xi)的程度,是由[0 ,1] 区间上的不同的数构成的非空有限集,且满足:0≤γ,η≤1且0≤γ++η+≤1 ,其中γ∈h(xi),η∈g(xi),γ+=max{γ|γ∈h对偶犹豫模糊语言集中的每个元素称为对偶犹豫模糊语言数,本文研究主要针对对偶犹豫模糊语言数展开。同时,为方便计算,称三元组为一个双重犹豫模糊语言数。
定义6[8]:设为两个任意的对偶犹豫模糊语言数,则有:
(1)和运算:

(2)积运算:

(3)数乘运算:

(4)幂乘运算:


(1)0≤D(d1,d2)≤1;
(2)当d1=d2时,D(d1,d2)=0 ;
(3)D(d1,d2)=D(d2,d1)。
证明如下:
(1)0≤D(d1,d2)≤1

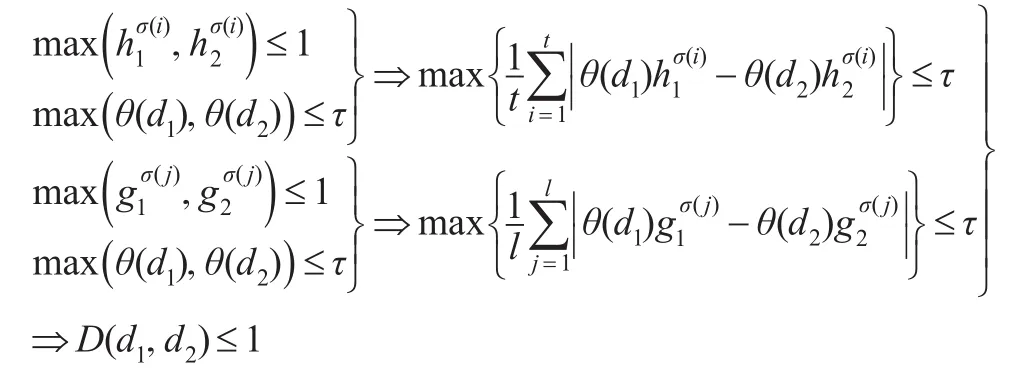
综上可得,对任意的d1和d2均有:0≤D(d1,d2)≤1。
(2)当d1=d2时,D(d1,d2)=0
d1=d2意味着d1和d2的语言术语下标,各隶属度值和非隶属度值均相等即:

因此,对任意的d1和d2均有:当d1=d2时,D(d1,d2)=0。
(3)D(d1,d2)=D(d2,d1)

因此,对任意的d1和d2均有:D(d1,d2)=D(d2,d1)。
2.2 对偶犹豫模糊语言数的比较方法
在决策过程中,语言术语之间的比较规则一直是研究重点。而在探讨对偶犹豫模糊语言数的比较规则时,得分函数和精确函数是重要的方式之一。Yang和Ju[8]提出对偶犹豫模糊语言的相关概念,同时也定义了相应的得分函数和精确函数:
定义 8[8]:设为任意的对偶犹豫模糊语言数,则其得分函数和精确函数可以表示为:

然而,通过观察可知,该得分函数和精确函数直接对对偶犹豫模糊语言数的隶属度和非隶属度求取平均值,没有考虑到隶属度和非隶属度的犹豫度和模糊性。因此,这种比较方法是具有一定的局限性的。
Zhu和Xu等[3]于2012年提出对偶犹豫模糊集,同时也提出基于对偶犹豫模糊集的扩展规则,运用此规则,在实质上是将对偶犹豫模糊集拆分成多个离散的直觉模糊数来进行运算的。因此基于此思路,本文提出对偶犹豫模糊语言扩展规则;将对偶犹豫模糊语言数拆分成多个离散的直觉语言,同时,考虑到对偶犹豫模糊语言数中的隶属度和非隶属度中元素的个数越多,其犹豫度和模糊性越强,该语言值越差。综上,本文定义基于直觉语言的对偶犹豫模糊语言数的得分函数和方差函数如下:


(1)当R(d1)>R(d2)时,则称d1优于于d2,记为d1≻d2;
(2)当R(d1)=R(d2)时:
若V(d1)<V(d2),则称d1优于d2,记为d1≻d2;
若V(d1)=V(d2),则称d1等于d2,记为d1~d2。
针对上述的例1,根据定义10和定义11可以得出R(d1)≈0.08,R(d2)≈0.0317。因为R(d1)>R(d2),所以d1≻d2,这是符合人类的主观直觉的。由此可见,新的得分函数和方差函数有助于进一步解决对偶犹豫模糊语言的大小比较问题。
3 基于对偶犹豫模糊语言TOPSIS法
3.1 对偶犹豫模糊语言的权重确定方法
第一步:构造基于对偶犹豫模糊语言的决策矩阵。决策者对每个备选方案在每个属性下运用对偶犹豫模糊语言进行打分,得到决策矩阵
第二步:计算属性cj(j=1,2,…,n)离差权重权。

第三步:计算属性cj(j=1,2,…,n)输出的信息熵及该属性熵权。信息熵反映了决策矩阵中各属性的信息量的大小,信息量越大,该属性越重要。根据基于对偶犹豫模糊语言的决策矩阵的定义可知,对于每个属性的信息熵可以划分为两个部分,一部分是属性值的得分期望输出,另一部分是属性值的不确定性程度即方差输出的。因此根据信息论可知,属性cj的熵定义为:


第四步:计算属性cj(j=1,2,…,n)的组合权重。根据上述分析求解可以得出离差权及熵权,利用加权平均法求得综合权重向量:

其中η表示决策者对熵权和偏差权重的偏重程度。
3.2 基于对偶犹豫模糊语言的TOPSIS排序法

其中T1和T2分别表示效益型属性集和成本型属性集。
第六步:利用综合权重向量计算得每个方案xi在各个属性下的评价值dij与正理想点之间的正混合加权偏好距离测度和与负理想点之间的负混合加权偏好距离测度:
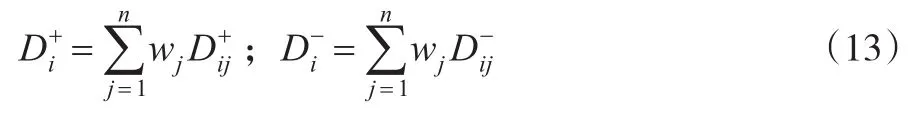
第七步:构造每个备选方案xi的贴近度。根据TOPSIS方法的思想,离正理想解的距离越近,离负理想解的距离越远,方案越优。因此,可构造贴近度计算公式为:

第八步:根据贴近度Ci的大小对方案进行排序。Ci越大,则该方案xi越优。
4 算例分析
第一步:构造基于对偶犹豫模糊语言的决策矩阵。决策者对每个备选方案在每个属性下运用对偶犹豫模糊语言进行打分,得到决策矩阵,根据上述对各属性的分析,可以看出,四个属性均为效益型属性因此规范化后的决策矩阵依然为:决策者给出的方案评估结果如表1所示。

表1 初始对偶犹豫模糊语言决策信息
第二步:根据公式(8)计算得属性cj(j=1,2,3,4)离差权重权,结果如下:

第三步:根据公式(9)和公式(10)计算得属性cj(j=1,2,3,4)输出的信息熵及该属性熵权,令β=0.8结果如下:

第四步:根据公式(11)计算得属性cj(j=1,2,…,n)的组合权重。此处取η=0.6:
w={0 .273,0.301,0.199,0.227}
第五步:基于上述对供应商基本信息,供应商的知识技术能力,供应商的企业文化和战略融合性,信息沟通能力的分析可以看出四个属性均为效益型属性,因此根据定义10和定义11可以确定每个属性下的正理想解和负理想解分别为:

第六步:根据公式(13)计算得每个方案xi在各个属性下的评价值aij与正理想点之间的正混合加权偏好距离测度和与负理想点之间的负混合加权偏好距离测度(i=1,2,3,4 ):

第七步:根据公式(14)可得每个备选方案xi的贴近度:

第八步:根据贴近度Ci的大小对方案进行排序。可以得出C3>C1>C2>C4,由此可知,方案的排列顺序是x3>x1>x2>x4。
5 结论
对偶犹豫模糊语言数不仅考虑到隶属度的信息的多种可能,还考虑到非隶属度信息的多种可能,这使得其在对语言偏好的描述上更精确,能避免决策中信息处理和计算过程中的信息丢失问题,在实际决策评价过程中价值更高,因此对对偶犹豫模糊语言的多属性决策方法进行研究有重要的理论和应用价值。语言比较是犹豫模糊语言研究的重要内容,也是犹豫模糊语言多属性决策的核心内容之一。本文提出基于对偶犹豫模糊语言的距离公式和扩展规则,并在此基础上定义新的得分函数和方差函数,通过实例,发现其在语言比较过程中更加精确。在多属性决策过程中,结合TOPSIS的思想,在属性权重未知的情况下,运用偏差权和熵权的组合权重法给出了多属性决策问题的排序方法。

