基于EEMD-PSO-SVM的月度CPI预测研究
邰晓红,刘 义
(辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105)
0 引言
居民消费价格指数(consumer price index,CPI)是一个用来反映居民家庭购买消费商品及服务的价格水平变动情况的重要宏观经济指标[1]。CPI涉及维系人民生计,关乎社会和谐,历来备受政府和民众关注。同时,CPI是价格总水平监测及调控、宏观经济分析及决策、国民经济核算的重要参考依据[1-5]。因此,科学精确的对CPI进行预测具有重要的现实意义。
目前,已经有一些学者对CPI进行预测研究,建立了一些预测模型。例如,神经网络模型[2]、ARIMA模型[3]、支持向量机模型[4]以及一些组合预测模型[5]等。这些模型对于CPI的预测具有重要意义。同时也存在一定的局限性,需要作进一步研究。需要说明的是,已有研究大多数是基于CPI的历史时序数据建立的预测模型。而CPI同时受到多重因素影响,其历史时序数据往往存在较大程度的波动。直接使用存在较大波动的CPI历史时序数据进行预测会在一定程度上影响CPI的预测结果。本文针对CPI历史时序数据的特点,提出了一种基于EEMD-PSO-SVM的月度CPI预测模型。在该模型中,首先采用EEMD对存在较大波动的CPI序列进行降噪分解,得到不同频率相对稳定的IMF序列和一个残余序列。然后采用PSO-SVM对得到的每个序列分别进行拟合预测。在此基础上,采用PSO-SVM对每个序列的预测结果进行融合,得到最终的月度CPI的预测结果。最后,以1994年1月至2017年5月的我国月度CPI为研究对象进行实际预测以验证模型的有效性和可靠性。
1 原理与方法
1.1 EEMD方法的基本原理
集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[6]是针对经验模分解(EMD)[7]的一种改进算法,其能够有效地解决采用EMD对时序数据进行分解时会出现虚假分量和模态混叠的问题。为了更加清晰地说明EEMD,这里首先对EMD进行简要介绍。
1.1.1 EMD方法的基本原理
EMD的基本思想是将一组时间序列数据转换成一系列带有不同尺度趋势或者波形的数据序列,其中产生的每一组数据序列称为一个特征模函数分量(intrinsic mode function,IMF)[7,8]。这里的IMF需要同时满足如下两个条件:(1)由IFM分量的极值点确定的包络线的均值为零,(2)IFM分量通过极值点的个数与通过零点的个数相等或者最多相差1个。
对于一组时间序列数据x(t),采用EMD对其进行分解的具体步骤如下。
(1)记u(t)和v(t)分别表示x(t)的极大值和极小值拟合成的包络线。则两条包络线的均值m1(t)可以表示为:

计算拟IMF分量h1(t):

判断h1(t)是否满足上述IMF条件,若满足则h1(t)即为第一个IMF分量;若不满足则将h1(t)作为原始时间序列,采用上述过程进行计算,直到经过k次筛选之后,得到的分量h1k(t)满足上述IMF的条件,此时得到的h1k(t)即为第一阶IMF分量,即为:

(2)记第一阶IMF分量得剩余信号为r1(t),r1(t)可以采用公式(4)计算,即:

依据上述过程对r1(t)进行分解,直到经过n此分解之后,rn(t)为一个单调函数时,分解结束。这样可以得到n个IMF分量c1(t),c2(t),…,cn(t)和n个IMF分量得剩余信号r1(t),r2(t),…,rn(t)。则原始时间序列可以表示为:

1.1.2 EMD方法的基本原理
由于采用EMD进行分解时容易产生虚假分量和模态混叠问题。EEMD通过引入高斯白噪声扰动并将多次分解的IMF进行集合平均进而可以效地解决EMD的上述问题。对于一组时间序列数据x(t),采用EEMD对其进行分解的具体步骤如下:
(1)对间序列数据x(t)叠加一组高斯白噪声序列ω1(t),可以得到叠加序列X(t),即:

(2)依据上文中EMD的分解过程,对X(t)进行分解,可以得到各阶IMF分解量:

(3)对间序列数据x(t)叠加不同的高斯白噪声序列ωi(t),并重复上述步骤,可以得到不同噪声序列对应的各阶IMF分解量,即:

需要说明的是ωi(t)的幅值为k的取值通常设置为0.2。
(4)由于高斯白噪声频谱的均值为零,可以采用式(9)计算x(t)对应的各阶IMF分量,即:

其中N表示加入高斯白噪声序列ωi(t)的总次数,通常取值为100。
1.2 PSO-SVM方法基本原理
SVM最早是在20世纪90年代由Vapnik等人首次提出的,SVM属于小样本、小概率事件类型神经网络模型。SVM与神经网络不同,它以统计学相关理论为基础,结构风险最小化为其学习原则,建立在小样本学习方法之上,具有非常强的非线性逼近能力和很好的泛化性能。SVM的算法具体如下[9]:
设输入量为x,首先将x通过映射Φ:Rn→H映射到高维特征空间H中,即:

拟合数据(xi,yi)目标函数式为:

式中,Φ(xi)·Φ(xj)为核函数,核函数有多种类型,本文选取径向基核函数,即:
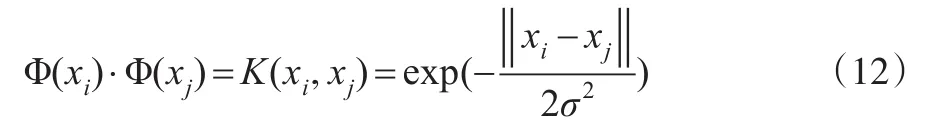
有:

得最终预测函数:

虽然SVM具有上述很多优势,但是SVM的惩罚参数c和核函数参数g对模型预测性能有较大的影响。为快速合理地确定SVM的c和g,本文引入PSO来优化SVM的c和g,给出了一种PSO-SVM算法。关于PSO的相关介绍可以参见文献[10]。关于PSO-SVM算法的具体描述如下:
(1)以训练样本的交叉验证均方误差(MSE Mean Squared Error)作为PSO的适应度函数;
(2)初始化PSO的种群,粒子速度v,进化代数,学习因子c1,c2和惯性权重w,初始化SVM参数c和g并确定c和g取值范围;
(3)依据式(10),计算交叉验证的PSO的适应度函数值;

式中,表示SVM预测值,yi表示实际值,n表示样本数量。
(4)寻找当前粒子的个体及全局最优值,若优于历史值,则对其进行更新;
(5)依据式(10)和式(11),更新粒子速度和位置。

式中,r1和r2为0到1区间的随机数,p为当前粒子位置,即SVM参数(c,g)的当前数值,pBest表示个体最优值,gBest表示整体最优值。
(6)若满足终止条件,则停止迭代该适应度值对应的c和g即为SVM最优的c和g;若不满足终止条件,则对个体和速度进行更新直到满足迭代终止条件。
1.3 基于EEMD-PSO-SVM的月度CPI预测流程
关于算法的描述如下:
(1)记历史月度CPI序列为x(t)。采用EEMD将x(t)进行分解可以得到n个不同频率相对稳定的IMF分量c1(t),c2(t),…,cn(t)和剩余信号rn(t)。
(2)分别对c1(t),c2(t),…,cn(t)和rn(t)采用滚动窗口的方式训练PSO-SVM,可以得到针对每个分量序列的预测模型,分别记为PSO-SVMc1,PSO-SVMc2,…,PSOSVMcn和PSO-SVMrn。
(3)分 别 采 用PSO-SVMc1,PSO-SVMc2,…,PSOSVMcn和PSO-SVMrn进行预测。以同一月份的PSOSVMc1,PSO-SVMc2,…,PSO-SVMcn和PSO-SVMrn的预测结果为自变量,该月份的实际CPI为因变量,再采用PSO-SVM对每个分量的预测结果进行融合,进而可以得到最终的月度CPI的预测结果。
2 实证分析
以1994年1月至2017年5月的我国月度CPI为研究对象(共281个月),其中1994年1月至2016年12月CPI数据作为训练样本用于建立模型,以2017年1月至2017年5月CPI数据作为测试样本用于检验模型。数据来源于国家统计局(http://www.stats.gov.cn/),具体数据见图1。图1中序号1表示1994年1月,序号281表示2017年5月。

图1 1994年1月至2017年5月的我国月度CPI数据
采用EEMD对原始CPI月度数据进行分解,最终得到7个不同频率相对稳定的IMF分量和一个剩余信号r(t),如图2所示。
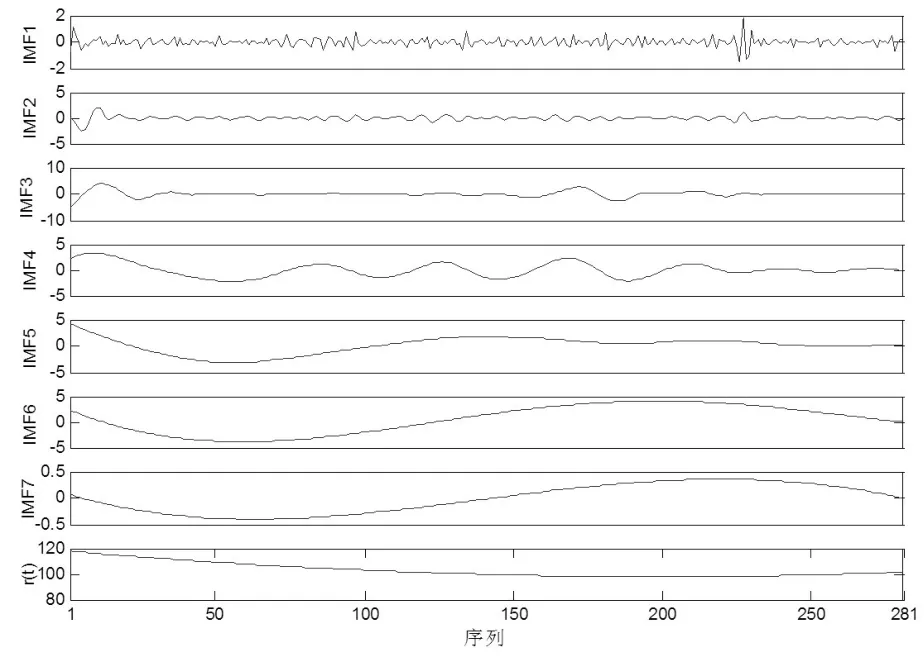
图2 EEMD分解结果
分别对c1(t),c2(t),…,c7(t)和r(t)采用滚动窗口的方式训练PSO-SVM,其中窗口大小设置为3。可以得到针对每个分量序列的预测模型,分别记为PSO-SVMc1,PSOSVMc2,…,PSO-SVMc7和PSO-SVMr。 分别采用PSO-SVMc1,PSO-SVMc2,…,PSO-SVMc7和PSO-SVMr对训练样本进行回代预测,并以各预测结果为自变量,该月份的实际CPI为因变量,再采用PSO-SVM对每个分量的预测结果进行融合。进行结果融合时PSO-SVM的相关参数设置如下:种群最大进化次数为200,种群数量为20,SVM的参数c和g的取值范围分别为[0.01,100]和[0.001,1000],PSO中的学习因子c1=1.5,c2=1.7,PSO中惯性权值w=1。得到适应度(交叉验证MSE)与进化次数的关系如图3所示。由图3可知,进化116代之后模型收敛,得到最终的MSE=0.01283,Best c=0.01,Best g=18.24。
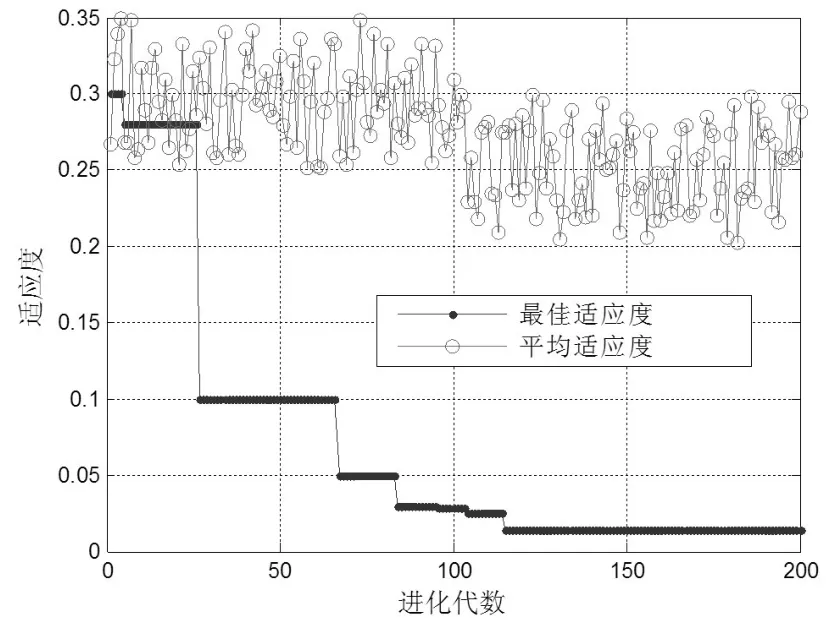
图3 适应度与进化代数的关系
由图4可知,建立的CPI预测的EEMD-PSO-SVM的月度CPI预测模型对训练样本数据的拟合效果较好。

图4 拟合结果
利用建立好的EEMD-PSO-SVM的月度CPI预测模型对2017年1月至2017年5月CPI数据进行预测,结果见表1。
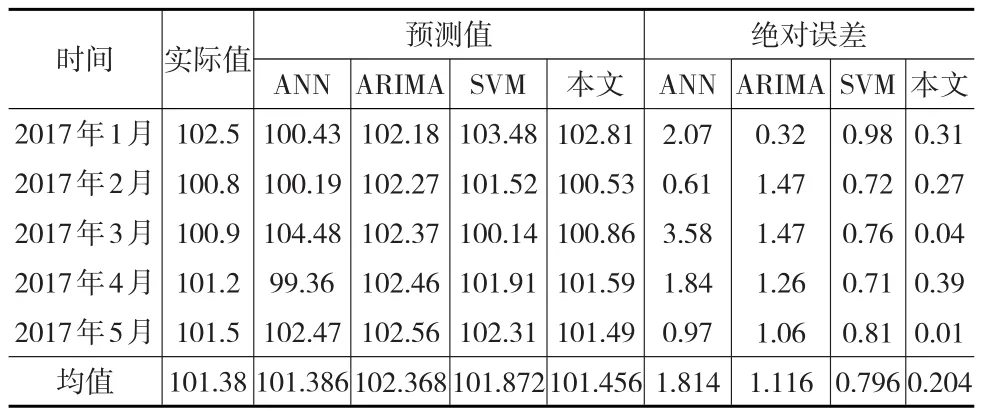
表1 预测结果及比较
为了便于比较和分析,表1中同时列出了采用人工神经网络(ANN)、自回归移动平均模型(ARIMA)和SVM的预测结果。由表1可知,本文提出的EEMD-PSO-SVM的月度CPI预测模型最大绝对误差为0.39,平均绝对误差为0.204,最小绝对误差仅为0.01,均小于低于ANN、ARIMA和SVM。本文提出的预测模型的平均相对误差仅为0.201%,能够满足实际的预测需求。
3 结论
(1)本文针对月度CPI时序数据的特点,提出了一种基于EEMD-PSO-SVM的月度CPI预测模型。在该模型中,EEMD能够对存在较大波动的CPI序列进行降噪分解,可以得到不同频率相对稳定的IMF序列和一个残余序列,为后续预测奠定良好的数据基础。PSO-SVM对带有小样本、非线性特点的CPI数据具有非常强的预测能力。本文将EEMD和PSO-SVM进行结合,综合发挥了二者的优势。
(2)以1994年1月至2017年5月的我国月度CPI为研究对象,采用提出的EEMD-PSO-SVM的月度CPI预测模型进行实际预测并与ANN、ARIMA、SVM进行比较。结果表明本文提出的预测模型的平均相对误差仅为0.201%,能够满足实际的预测需求,为CPI科学准确的预测提供了一种新的方法。

