两参数对数正态分布与威布尔分布的近似极大似然估计

顾蓓青，徐晓岭，王蓉华

（1.上海对外经贸大学 统计与信息学院，上海 201620；2.上海师范大学 数理学院，上海 200234）

0 引言

在可靠性试验中，逐步增加的Ⅱ型截尾寿命试验在实际中经常会碰到，具有理论与应用价值，而在国内外对此场合却很少有人进行研究，目前主要是研究定数及定时截尾场合下Weibull分布参数的点估计和区间估计。譬如当组织一批价值昂贵的产品做寿命试验时，若已有一部分产品失效发生时，考虑到试验费用等因素，经常会从未失效的产品中抽取一部分产品移离试验现场，这样可以大大节约成本。又例如在寿命试验过程中为了解产品的失效机理和退化情况，以便更好地设计产品，需要从尚未失效的产品中选取部分产品进行解剖分析。再例如观察患某种疾病的病人的生存情况时，医生可能仅仅观察到一部分病人的生存寿命，而另一部分患者可能不到医院来就诊而无法了解其生存寿命，即这一部分病人失去观察。

逐步增加的Ⅱ型截尾试验是Ⅱ型截尾的一个推广，它是在n个产品的样本中先观察到r1个失效，然后剩下的n-r1个未失效的产品中有n1个被移离试验，留下n-r1-n1个产品继续试验，当再有r2-r1个产品失效后,将剩余仍未失效产品中的n2个被移离试验，试验如此进行下去，直到有一定数量的产品失效为止就终止试验，试验数据如表1所示。

表1 逐步增加的Ⅱ型截尾寿命试验数据

其中r0=0，n0=0，x(0)=0，ri≥1，ni≥0，i=1，2，…，k，k≥1，而nk为最后试验结束时未失效的产品数。特别地，（1）当ni=0，i=1，2，…，k-1时，便为通常的定数截尾寿命试验；（2）当r1=1，r2=2，…，rk=k时，通常称为逐次截尾。

徐晓岭和王蓉华（2003）[1]给出Weibull分布在逐步增加的Ⅱ型截尾寿命数据参数的极大似然估计与逆矩估计，并通过Monte-Carlo模拟考察了估计的精度，认为极大似然估计优于逆矩估计。王炳兴（2004）[2]讨论了Weibull分布基于定数逐次截尾寿命数据的参数估计，得到了参数的逆矩估计量和区间估计，模拟结果显示在中小样本情况下所给估计量优于参数的最大似然估计。李凤等（2008）[3]基于逐步增加的II型截尾，讨论了Weibull分布的Bayes估计，在平方损失和LINEX损失下，利用Lindely Bayes近似算法得到了形状参数、尺度参数、失效率函数以及可靠度函数的极大似然估计和Bayes估计，并运用Monte-Carlo方法对各估计结果的RMSE，进行了模拟比较，表明了LINEX损失下的结果更有效。李中恢（2012）[4]在逐步II型截尾样本下讨论了逆Rayleigh分布参数的估计问题，给出了参数的最大似然估计，并在三种不同的损失函数下给出了参数的Bayes估计和区间估计。李琼和武东（2012）[5]对Pareto分布场合逐步增加II型截尾样本进行了贝叶斯分析，利用马尔可夫链蒙特卡罗方法给出了参数的贝叶斯估计，并通过蒙特卡罗模拟和应用实例表明该贝叶斯估计是有效的。卫超和师义民（2014）[6]基于逐步II型混合截尾寿命试验数据，导出了Pareto分布参数的极大似然估计和不同先验分布下的Bayes估计，并利用Monte-Carlo模拟方法对估计的结果进行了对比分析。杨君慧等（2014）[7,8]基于逐步增加II型截尾试验，在单参数情况下，利用极大似然估计方法给出了广义指数分布形状参数和可靠度函数的极大似然估计，并证明了极大似然估计的相合性和渐近正态性。以及在熵损失和加权平方损失函数下，给出参数和可靠度函数的贝叶斯估计，并运用Monte-Carlo方法对估计结果进行了模拟比较。

此外，文献[9]中指出，对于一些分布，如指数分布、Rayleigh分布、Weibull分布的参数极大似然估计并没有显示表达式。因此，为了改进极大似然估计方法，提出了近似极大似然估计的方法。王蓉华等（2000）[10]给出了在定数截尾数据缺失场合下两参数对数正态分布参数的近似极大似然估计。顾益明（2011）[11]给出了单参数指数、两参数指数、两参数Weibull及两参数对数正态分布型产品在基于分组型数据下参数的近似极大似然估计。杨振海和程维虎（2004）[12]讨论了基于Logistic总体II型截尾样本分布参数的近似极大似然估计。王娟和陆志峰（2008）[13]针对对数正态分布的一般II型逐步删失样本，从似然方程出发，采用一种近似方法将非线性部分线性化求解极大似然估计，并同经典的牛顿迭代法进行数值比较，结果基本相同，表明该方法是一种较好的求参数估计值的方法。张莉（2009）[14]基于指数分布下的分组数据，研究了步加试验中参数的近似极大似然估计方法，并通过蒙特卡罗模拟说明方法是可行且有效的。

近似极大似然估计方法涉及到函数在点ξi处一阶泰勒展开，其中ξi满足F(ξi)=pi，在定数截尾试验下而在逐步增加Ⅱ型截尾试验下，本文考虑l=1，2，…，k或者两种泰勒展开方式（分别记为方法一和方法二），分别给出两参数对数正态分布和威布尔分布的近似极大似然估计，并在这两种泰勒展开方式下比较近似极大似然估计的精度，通过Monte-Carlo模拟发现后者更优。

1 对数正态分布的近似极大似然估计

假设有n个产品进行寿命试验，产品的寿命X服从两参数对数正态分布，即X～LN(μ，σ2)，其分布函数FX(x)和密度函数fX(x)分别为：

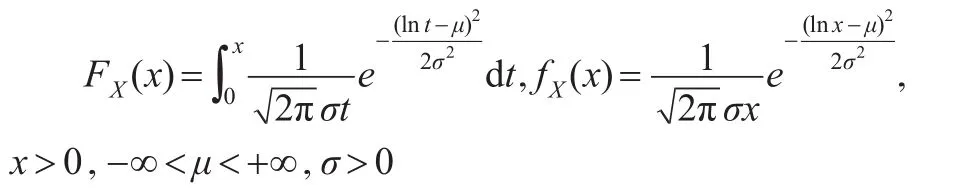
其中μ，σ2分别称为对数均值和对数方差。

若令Y=lnX，则Y～N(μ，σ2)，其分布函数FY(y)和密度函数fY(y)分别为：

将n个寿命服从两参数对数正态分布LN(μ，σ2)的产品做逐步增加的II型截尾寿命试验，试验数据如表1所示。

令y(i)=lnx(i)，i=1，2，…，r1，…，rk，依赖于数据y(1)，y(2)，…，y(r1)，…，y(rk)的似然函数为：

由此：

记ξi满足 Φ(ξi)=pi，i=1，2，…，rk，即ξi=Φ-1(pi)，i=1，2，…，rk

其中：

此时有：

化简式（1）：

其中：

将式（3）代入式（2）化简得：

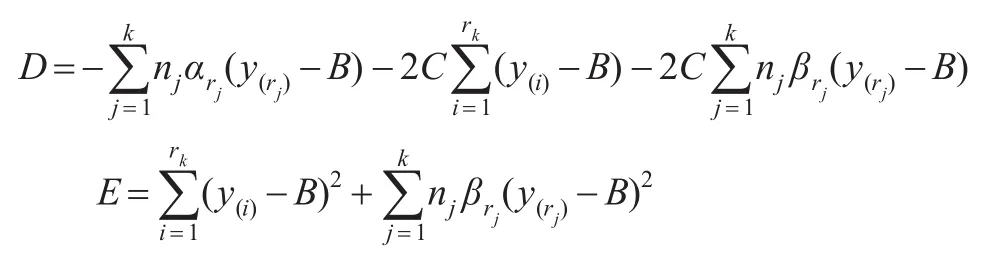
此时方程变形为：Aσ2+Dσ-E=0

则参数σ的近似极大似然估计为：

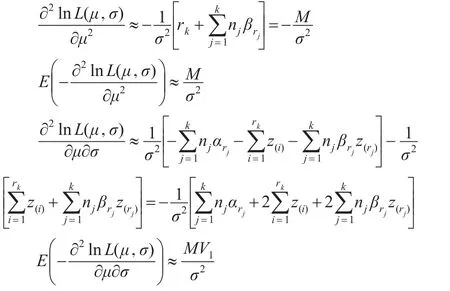
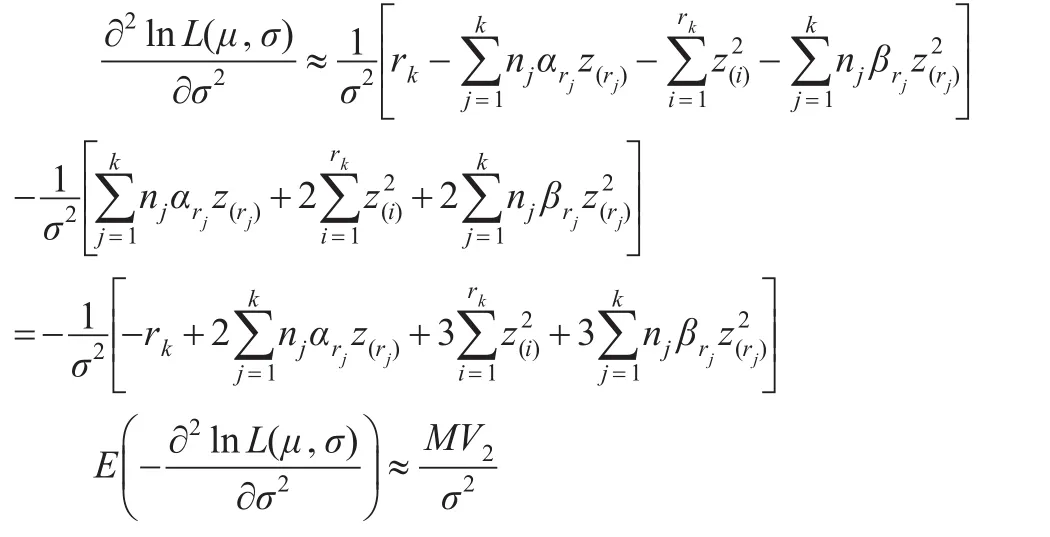
其中：

2 威布尔分布的近似极大似然估计

假设有n个产品进行寿命试验，产品的寿命X服从两参数威布尔分布，即X～W(m，η)，其分布函数FX(x)和密度函数fX(x)分别为：

其中m＞0为形状参数，η＞0为刻度参数。

Z的分布函数FZ(z)和密度函数fZ(z)分别为：

将n个寿命服从两参数Weibull分布W(m，η)的产品做逐步增加的II型截尾寿命试验，试验数据如表1所示。

令T(i)=lnX(i)，t(i)=lnx(i)，i=1，2，…，r1，…，rk，依赖于数据t(1)，t(2)，…，t(r1)，…，t(rk)的似然函数为：

记ξi满足FZ(ξi)=pi，i=1，2，…，rk，即：

即：

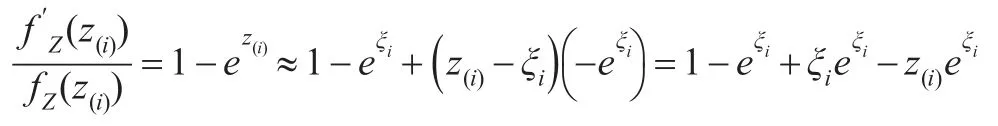
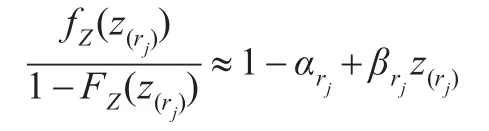
此时有：

化简式（4）：

将式（6）代入式（5）化简得：

记：

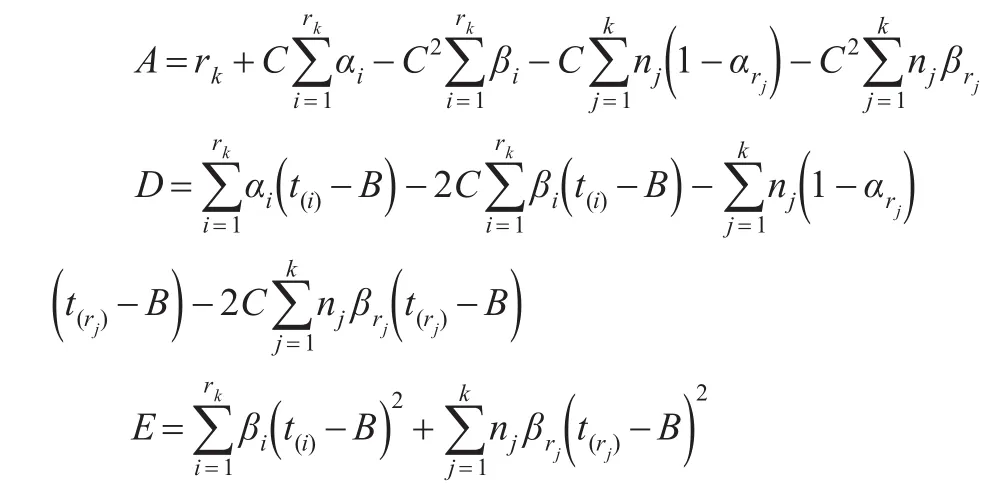
此时方程变形为：Aσ2+Dσ-E=0

则参数σ的近似极大似然估计为：

因此，参数η和m的近似极大似然估计分别为：

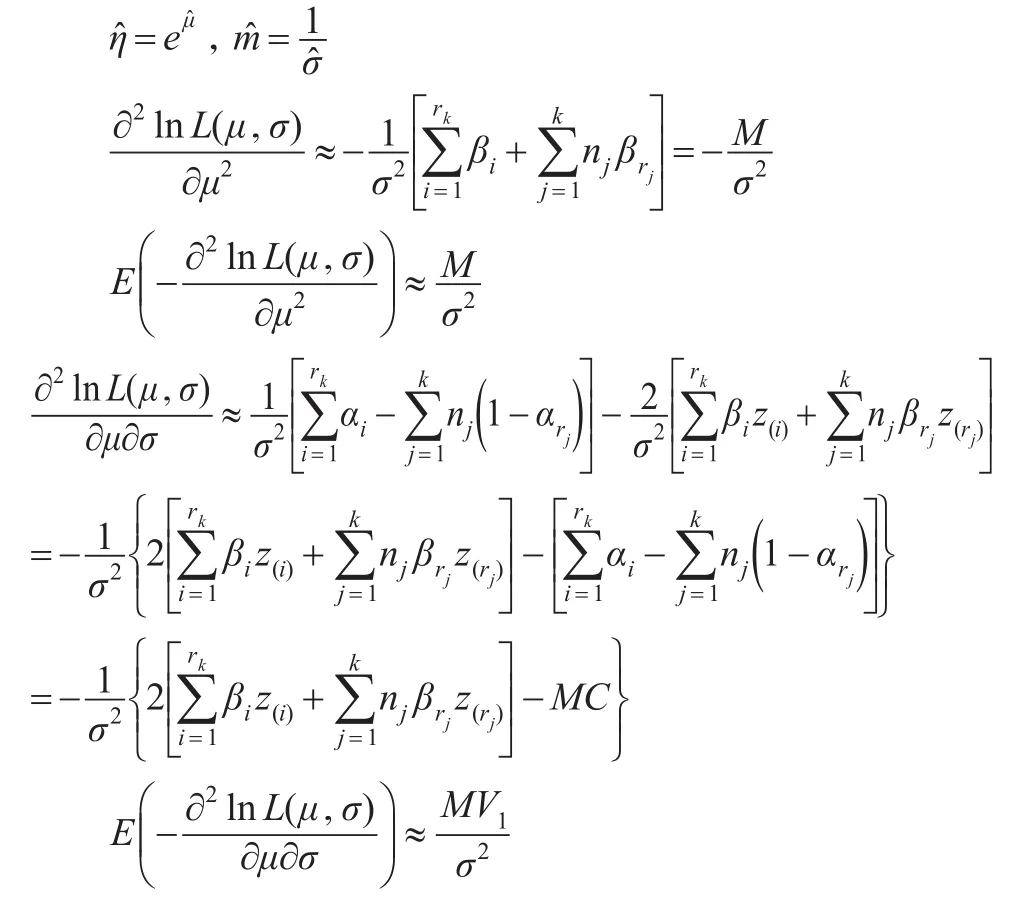
3 模拟比较及算例

表2 对数正态分布的近似极大似然估计比较

表3 威布尔分布的近似极大似然估计比较

例 1：取对数正态分布LN(μ，σ2)的参数真值为μ=1，σ=1，样本容量n和截尾个数为n=20，r1=5，n1=2，r2=10，n2=2，r3=15，通过Monte-Carlo模拟产生逐步增加的Ⅱ型截尾样本数据为：-1.4247，-0.6394，-0.3934，0.1061，0.2061，0.6364，0.7162，1.0006，1.0378，1.0543，1.0669，1.1496，1.4043，1.4488，2.1458，利用本文方法，由方法一得到参数μ，σ的近似极大似然估计为μ̂1=0.9136，σ̂1=0.9920 ，由方法二得到参数μ，σ的近似极大似然估计为μ̂2=0.9167，σ̂2=0.9926 。

例2：取威布尔分布W(m，η)的参数真值为m=2，η=1，样本容量n和截尾个数为n=30，r1=8，n1=4，r2=15，n2=3，r3=20，通过Monte-Carlo模拟产生逐步增加的Ⅱ型截尾样本数据：-2.5044，-1.2816，-0.9434，-0.9004，-0.8201，-0.7804，-0.7768，-0.7563，-0.6990，-0.3452，-0.3081，-0.2960，-0.1561，-0.1545，0.0164，0.1370，0.1512，0.2321，0.2412，0.2873，利用本文方法，由方法一得到参数m，η的近似极大似然估计为m̂1=2.0759，η̂1=0.8549 ，由方法二得到参数m，η的近似极大似然估计为m̂2=1.9820，η̂2=1.0226。

4 结论

在推导参数近似极大似然估计的过程中会关系到函数的一阶泰勒展开，本文在逐步增加Ⅱ型截尾寿命试验下考虑了两种泰勒展开方式，并且针对两参数对数正态分布和威布尔分布分别推导了参数的近似极大似然估计，并在这两种泰勒展开方式下比较了估计的精度，通过大量的Monte-Carlo模拟发现利用方法二的泰勒展开方式得到的近似极大似然估计略优。